Čtvrtá série začátečnické kategorie třicátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 33-Z4-1: Střílení do terče
- 33-Z4-2: Hesla nebo odpad?
- 33-Z4-3: Kluzké bludiště
- 33-Z4-4: Opačná úloha
 33-Z4-1 Střílení do terče (Zadání)
33-Z4-1 Střílení do terče (Zadání)
Naším cílem je zjistit, které kulky trefily terč. Z matematického pohledu můžeme na terč nahlížet jako na kruh se středem (x,y) a poloměrem r. Pro bod (a,b) na jeho obvodu platí následující vzoreček:
To můžeme nahlédnout z obrázku a znalosti Pythagorovy věty:
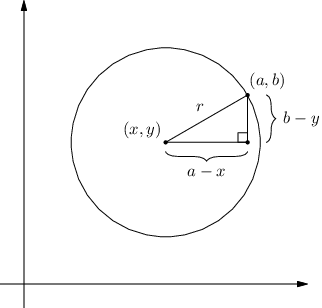
Aby se kulka trefila do terče, musí být její vzdálenost od středu terče menší než poloměr terče. Proto se vlastně ptáme, zda je pro souřadnice dopadu kulky (shotx, shoty) splněna následující nerovnice:
Při vyhodnocování tedy budeme postupně načítat souřadnice dopadu jednotlivých kulek ze vstupu a pro každou z nich vyhodnotíme levou část nerovnice. Pokud bude výsledek menší než r2, vypíšeme pořadové číslo kulky na výstup, jinak neděláme nic.
 33-Z4-2 Hesla nebo odpad? (Zadání)
33-Z4-2 Hesla nebo odpad? (Zadání)
Pro každé heslo potřebujeme umět rozhodnout, zda odpovídá zadanému předpisu. Předpis vůči heslu budeme muset kontrolovat po znacích, tomu se nevyhneme. Ale jak si postup co nejvíce zjednodušit?
Protože se hvězdička vyskytuje v předpisu právě jednou, můžeme předpis v místě hvězdičky rozdělit, a pak na něj nahlížet jako na předpis pro začátek (prefix) a na předpis pro konec (sufix) hesla. Heslo tedy budeme kontrolovat dvakrát – zda začátek hesla odpovídá prefixu předpisu a zda konec hesla odpovídá sufixu předpisu.
Zde si můžeme všimnout, že kontrola konce hesla vůči sufixu je ekvivalentní kontrole otočeného hesla vůči otočenému sufixu, což nám umožní zjednodušit implementaci. Dále je důležité si uvědomit, že když při kontrole dojdeme na konec předpisu, zbývající znaky hesla můžeme vesele ignorovat. Tyto znaky se totiž v předpisu schovají pod hvězdičku.
Výše popsaný postup kontroly má jeden problém – kontrola prefixu i sufixu slova může uspět, ačkoli by heslo projít nemělo, neboť je kratší než zadaný předpis (to se stane, když se prefix a sufix předpisu překrývají). Proto ještě musíme provést kontrolu délky hesla.
Časová složitost je lineární vzhledem k součtu délek hesel na vstupu, paměť nám stačí vždy jen délku jednoho hesla a prefixu.
 33-Z4-3 Kluzké bludiště (Zadání)
33-Z4-3 Kluzké bludiště (Zadání)
Tuto úlohu můžeme vcelku přímočaře vyřešit prohledáváním do šířky. Budeme si značit již navštívená políčka (na začátku je to jenom start) a na každém políčku si budeme udržovat odkaz na políčko, ze kterého jsme na něj přišli.
Na začátku si vložíme startovní políčko do fronty a pak pro každé políčko z fronty opakujeme následující postup: Najdeme všechna nenavštívená políčka, na která se z aktuálního políčka umíme doklouzat (tedy nejvýše čtyři políčka ve všech čtyřech směrech), ta lehce najdeme odkrokováním v daném směru, než narazíme do zdi. Nalezená políčka označíme za navštívená, uložíme si k nim odkaz na aktuální políčko (ten se bude hodit pro vypsání cesty) a vložíme políčka do fronty.
Pokud během procházení narazíme na cílové políčko, tak můžeme prohledávání
ukončit a pak již jen vypíšeme cestu rekonstruovanou přes zpětné odkazy. Začneme
z cíle a podíváme se na zpětný odkaz. Podle toho, kam jsme museli z minulého
políčka jít, tak si do cesty přidáme N, D, P, nebo L
a pokračujeme s dalším políčkem, dokud nedojdeme na start. Ale pozor na to, že
teď jsme cestu zrekonstruovali pozpátku, musíme ještě cestu před vypsáním otočit.
A to už je správné řešení.
Jak dlouho takový postup trvá? Pro bludiště velikosti R×S může zpracování jednoho políčka trvat až O(R+S) (musíme proklouzat celý řádek a sloupec). Pro každé políčko to uděláme jednou, políček je RS, takže celková časová složitost je O(RS(R+S)).
Rychlejší řešení s grafy
Toto řešení je zbytečně pomalé, zlepšit se dá postavením vhodného grafu nad bludištěm. Ono už samotné bludiště je vlastně grafem s vrcholy odpovídajícími políčkům a s hranami vedoucími vždy na sousední políčka. My si ale postavíme lepší graf, aby nám klouzání netrvalo tak dlouho.
Vrcholy našeho grafu budou také políčka bludiště, ale hrany budou pro každý vrchol vést na místa, do kterých se z něho umíme doklouzat. Navíc si zavedeme speciální případ pro to, pokud při klouzání potkáme cíl – v tom případě bude hrana směřovat do něho.
Jedná se o orientovaný graf, protože z políčka, do kterého jsme se právě doklouzali, nemusí existovat hrana nazpět (typicky protože se cestou nazpět dokloužeme dál). Počet vrcholů a hran v něm bude odpovídat počtu vrcholů a hran v původním bludišti (tedy RS vrcholů a až 4RS hran), ale hrany si zkonstruujeme šikovněji.
Jak si pořídíme ty správné hrany? Můžeme si vyrobit rekurzivní funkci, která dostane políčko a směr a vrátí, kam se z daného políčka v tomto směru dokloužeme. Pokud je tento směr pro dané políčko již spočítaný, tak funkce vrátí uloženou hodnotu a hotovo. Pokud směr ještě spočítaný není, tak se funkce podívá na vedlejší políčko v daném směru. Pokud je vedlejší políčko…
- zeď, tak výsledek je aktuální políčko,
- cíl, tak výsledek je cíl samotný,
- jinak funkce zavolá sama sebe na vedlejší políčko (tomuto říkáme rekurze).
Když máme tuto funkci, tak nám stačí projít všechna políčka a pokud ještě nemají spočítaný nějaký směr, tak na nich zavoláme tuto funkci s daným směrem. Tím si pořídíme tyto rychlé hrany ze všech políček bludiště.
Jak dlouho tento předvýpočet trvá a jak nám pomůže? Tím, že si funkce ukládá již spočítané směry u políček, tak ji pro každé políčko a směr provedeme nejvýše jednou, tedy celý předvýpočet zabere čas O(RS).
Díky spočítaným hranám pak již při procházení nemusíme pokaždé krokovat, ale použijeme rychlé hrany a jedno políčko tak při prohledávání zpracujeme za konstantní čas (O(1)). Celé prohledávání pak zvládneme v čase O(RS), což je tedy i celková časová složitost algoritmu. Oproti prvnímu pomalejšímu řešení to může představovat rozdíl v čase běhu jedna sekunda versus velké desítky sekund.
 33-Z4-4 Opačná úloha (Zadání)
33-Z4-4 Opačná úloha (Zadání)
Zkusme nejdříve odpovědět druhou otázku: Jakou časovou složitost má program? První podmínka (pokud S < K), nám zvětší index j o jedna. U druhé podmínky se nám zvětší index i o jedna. Třetí podmínka není zajímavá, protože tam hned končíme. Jelikož provedení jednoho cyklu nám trvá konstantně dlouho (provádíme maximálně tři porovnání a dvě sčítací operace), tak časová složitost závisí na tom, kolik provedeme opakování cyklu.
Když si rozmyslíme, že indexy i a j jen zvětšujeme, tak každé číslo můžeme navštívit maximálně dvakrát. Poprvé ho přičítáme do sumy S (při zvětšení indexu j) a podruhé ho odčítáme od sumy S (při zvětšení indexu i). Z toho víme, že provedeme asymptoticky 2n operací. Tedy časová složitost algoritmu je O(n). Paměťová složitost je O(1) – pamatujeme si tři proměnné.
Nyní víme, že náš algoritmus je příjemně rychlý, ale je správný?
Pro celá kladná čísla nám algoritmus funguje. Zkusme přijít na to proč. U celých kladných čísel nám platí následující: Mějme podposloupnost mezi indexy i a j. Pokud do této podposloupnosti přidáme jedno číslo (posuneme j o jedna), tak se součet podposloupnosti vždy zvětší a naopak pokud podposloupnost zmenšíme o jedna (posuneme i o jedna), tak se součet vždy zmenší.
Z toho nám platí, že pokud součet podposloupnosti je menší než hodnota K a tuto podposloupnost zmenšíme, tak součet bude pořád menší než hodnota K. Toto platí samozřejmě i naopak. Z toho dostáváme, že pokud součet podposloupnosti potřebujeme zvětšit, tak musíme podposloupnost rozšířit, a toto platí i naopak. Tímto jsme ale dostali algoritmus popsaný v zadání, tudíž algoritmus je správný.
Pro čistě záporná čísla nám algoritmus nefunguje. Uvažme třeba
vstup -4 -1 a hledané K = -5. Sečtení hodnot -4 a -1 je
očividně výsledek -5, ale náš algoritmus toto nenajde.
Při první opakování není první podmínka S < K pravdivá
(-4 není menší jak -5) a provede se tak druhá podmínka. Na konci prvního
opakování má S hodnotu 0.
Není ale těžké uvědomit si, že pro záporná čísla by šlo algoritmus lehce opravit. Buď bychom mohli celý vstup vynásobit -1 nebo bychom mohli otočit nerovnosti v algoritmu.
Pro celá čísla nám algoritmus také nefunguje. Uvažme třeba vstup 5 -1
a hledané K = 4. Součet čísel 5 a -1 je 4, ale algoritmus toto nenajde.
Narozdíl od čistě záporných čísel nelze algoritmus ani nijak lehce opravit,
v tomto případě totiž nemůžeme o posunutí jednoho ani druhého konce intervalu
nic prohlásit (obě posunutí mohou součet zvětšit i zmenšit) a tím padá hlavní
myšlenka algoritmu.