Pátá série třicátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 33-5-1: Šotek a obrazy
- 33-5-2: Zakázaná písmena
- 33-5-3: Těžký vozík
- 33-5-4: Nevěřící Bob
- 33-5-S: Globální iluminace a path tracing
- 33-5-X1:
 33-5-1 Šotek a obrazy (Zadání)
33-5-1 Šotek a obrazy (Zadání)
Šotek nám zpřeházel obrazy očíslované od 1 do N podle nějakého polynomu pátého stupně, který máme zadaný na vstupu. Jak je seřadit zpátky? Zkoušet invertovat polynom by bylo složité, ale to naštěstí nepotřebujeme. Nám stačí jenom napárovat N funkčních hodnot polynomu na čísla od 1 do N.
Vyhodnotit polynom pátého stupně zvládneme v konstantním čase (je to jen několik násobení a sčítání), takže si můžeme v čase O(N) zkonstruovat následující posloupnost dvojic:
Pokud by se nám povedlo tuto posloupnost seřadit podle funkčních hodnot od nejmenší po největší, tak pak budou dvojice přesně odpovídat pořadí obrazů (protože šotek je také seřadil podle funkčních hodnot). Na rozdíl od přeházených obrazů však budeme mít jednu informaci navíc – číslo z rozsahu 1 až N udávající původní pořadí obrazu. Takže pokud se nám podaří dvojice seřadit podle funkčních hodnot, tak pak stačí jen projít přes všechny dvojice a vydat informaci o původním pořadí obrazu.
Jak ale seřadit funkční hodnoty rychle? Běžné třídící algoritmy využívající jen vzájemné porovnávání prvků nemohou být rychlejší než O(N log N), za což dle zadání plné body nebudou, co s tím? Budeme potřebovat využít nějaké speciální vlastnosti čísel a použít algoritmus, který nedělá jen porovnávání dvojic.
Přihrádkové třídění
První, co by nás mohlo napadnout, je přihrádkové třídění neboli Radix sort (ten je speciální případ Bucket sortu). To využívá toho, že jsou čísla ke třídění jen z nějakého omezeného rozsahu a dá se jimi indexovat pole. Vyrobíme si přihrádky pro každé číslo z tohoto rozsahu a pak čísla procházíme a rozhazujeme je do jednotlivých přihrádek (což mohou být třeba spojové seznamy). Na konci jen projdeme všechny přihrádky a „slepíme“ je za sebe.
Jednoúrovňové použití pro nás nedává úplně smysl, ale pravá síla přihrádkového třídění přichází tehdy, když ho použijeme víceúrovňově. V prvním průchodu můžeme třídit čísla podle jejich poslední cifry, pak podle předposlední a tak dále až k první cifře. Díky tomu, že je přihrádkové třídění stabilní (nemění pořadí prvků se stejným třídícím klíčem), tak nám na konci vyjde seřazená posloupnost.
V našem případě by bylo nejlepší pořídit si pole N přihrádek a rozházet do nich čísla podle zbytku po dělení N. Pak je můžeme celočíselně vydělit N a celý postup opakovat, dokud nebudou čísla seřazená (vlastně jsme tím převedli čísla do soustavy o základu N). Jeden průchod přihrádkového třídění nám zabere čas O(N), kolik průchodů ale potřebujeme udělat?
Maximální hodnotu, která nám může vylézt z polynomu pátého stupně, lze odhadnout jako O(N5). S úplně čistým svědomím však nelze prohlásit, že nám vždy stačí pět průchodů přihrádkového třídění, záleží totiž ještě na konstantách u samotného polynomu. Správný časový odhad přihrádkové třídění by tedy ještě musel počítat s maximem M, které nám může z polynomu vyjít, a výsledná časová složitost by tak byla O(N logN M).
Monotónnost
Pojďme využít ještě jiné vlastnosti polynomu pátého stupně, která nám již umožní dosáhnout skutečně lineární časové složitosti vzhledem k počtu obrazů.
O polynomu prvního stupně (třeba f(x) = 4x) můžeme říci, že je v celém svém rozsahu monotónní (tedy buď klesá nebo stoupá, ale nemění se to). U polynomu druhého stupně podobně platí, že má nejvýše dva monotónní úseky (třeba f(x) = -x2 + 2x od minus nekonečna do jedničky roste a pak od jedničky do nekonečna zase klesá). Podobná vlastnost existuje i u polynomů vyšších stupňů a lze prohlásit, že polynom k-tého stupně má nejvýše k monotónních úseků (může jich mít ale i méně, třeba f(x) = x5 má jen jeden monotónní úsek, ačkoli má stupeň 5).
Díky této vlastnosti víme, že funkční hodnoty v našem seznamu dvojic jsou v některých úsecích seřazené. Úloha se nám tak zjednodušuje na nalezení těchto úseků a jejich slití dohromady.
Pojďme nejprve vyřešit jejich nalezení – budeme si vytvářet seznamy prvků jednotlivých úseků, u kterých si navíc budeme pamatovat jejich směr (jestli daný úsek stoupá nebo klesá). Na začátku do prvního úseku vložíme první dva prvky a podle nich určíme, jestli první úsek stoupá nebo klesá. Pak budeme procházet další prvky, a dokud bude další prvek vyhovovat směru, tak ho přidáme do aktuálního úseku, jinak založíme nový úsek s opačným směrem a vložíme prvek do něj. To zvládneme v O(N). Pro jednoduchost slévání si ještě můžeme na konci otočit klesající úseky na rostoucí, což také zabere maximálně čas O(N).
Nyní máme (nejvýše) pět seznamů, ve kterých jsou uspořádané funkční hodnoty, zbývá nám udělat jejich slití. To bude podobné slévání, které se používá v Mergesortu – v každém kroku se podíváme na první prvek všech seznamů, nalezneme ten nejmenší z nich, odebereme ho a vložíme ho do finálního pole. Tento postup opakujeme N-krát a na konci dostaneme seřazené pole. Každý krok nám zabere konstantně mnoho času (porovnání pěti hodnot), takže celkový čas tohoto slévání, a tedy i celého třídění využívajícího monotónnost je O(N).
Pokud si takto seřadíme dvojice z úvodu podle funkčních hodnot, tak už lehce vydáme správné pořadí obrazů.
 33-5-2 Zakázaná písmena (Zadání)
33-5-2 Zakázaná písmena (Zadání)
První, čeho je dobré si všimnout (a trochu to naznačovaly i limity uvedené v zadání),
je, že při nahrazování písmen může délka řetězce velmi rychle narůstat (konkrétně
exponenciálně). Představme si například nahrazovací pravidla
a → bbbb,
b → cccc,
…,
y → zzzz,
z → 0000.
Potom si snadno rozmyslíte, že z jednoho a se stane řetězec nul dlouhý
426=252. Takovýto řetězec by zabral 4.5 petabajtů paměti, nemluvě
o tom, jak dlouho by trvalo jej sestrojit. Tedy určitě si nemůžeme dovolit
konstruovat celý výsledný řetězec.
Nyní trochu terminologie. Náhrada nějakého znaku c (budeme značit sub(c)) je prostě pravá strana jeho nahrazovacího pravidla (může obsahovat písmena i jeho číslice). Oproti tomu expanze nějakého řetězce s (značíme exp(s)) je řetězec, který vznikne, pokud začneme s s a nahrazujeme podle pravidel, dokud to jde. Expanze vždy obsahuje pouze číslice.
Nejprve zkusíme zodpovědět otázku, která s úlohou na první pohled tolik nesouvisí. Rádi bychom pro každé písmeno spočítali délku jeho expanze.
To snadno vyřešíme pomocí dynamického programování. Délku expanze jednoho písmene spočítáme tak, že se podíváme na jeho náhradu, rekurzivně spočteme délky expanzí všech písmen v této náhradě a sečteme je. Navíc si pořídíme cache na už spočítané výsledky, takže nikdy nebudeme počítat expanzi stejného písmene dvakrát.
Výpočet pro jedno písmeno nás stojí (nepočítaje rekuzivní volání) O(ℓ), kde ℓ je délka jeho náhrady. Protože pro každé písmeno spouštíme výpočet nejvýše jednou, celkem spotřebujeme čas O(L), kde L je součet délek všech nahrazovacích pravidel.
Nyní si představme, že máme nějaký řetězec s a navíc známe délku expanzí všech
znaků. Pak si pro každý znak c v s můžeme spočítat, na jaké pozici v exp(s)
začíná expanze tohoto znaku. To je prostě součet délek expanzí všech
předcházejících znaků. Například pro řetězec
aba1b s délkami expanzí a: 100, b: 50:
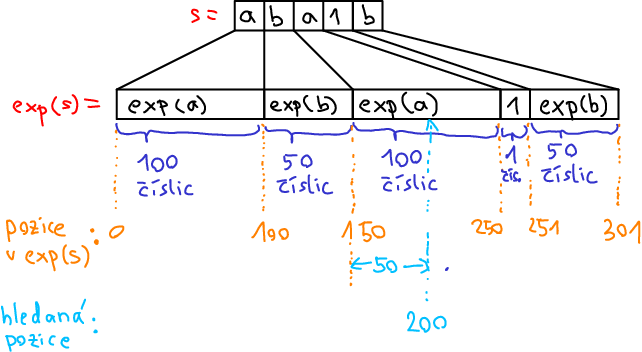
Nyní například, kdybychom chtěli najít číslici na pozici 200 v exp(s), víme
že bude ležet uvnitř expanze druhého a, konkrétně na pozici 50. Jinými slovy
potřebujeme najít znak na pozici 50 v exp(a), což můžeme udělat rekurzivní
aplikací stejného postupu na sub(a).
Z toho plyne přímočarý rekurzivní algoritmus Cislice(s, i) na nalezení i-té číslice v exp(s) pro nějaký řetězec s:
- Pro každý znak urči pozici v exp(s), na které začíná jeho expanze. Pro k-tý znak s si tuto pozici označíme pos(k). Např. v příkladu výše pos(2)=150.
- Urči, do expanze kterého znaku s patří pozice i. Říkejme tomuto znaku c, jeho
pozici v s pak k. Víme, že expanze c začíná na pozici pos(k) v exp(s).
Např. v příkladu výše c=
a, k=2. - Pokud c je číslice, vrať c.
- Pokud c je písmeno, vrať Cislice(sub(c), i-pos(k)).
Výpočet Cislice(s,i) trvá čas O(|s|), nepočítaje rekurzivní volání. Označme si K délku výchozího řetězce na vstupu. Pak v našem programu pro zjištění jedné číslice proběhnou následující volání funkce Cislice:
- Jedno volání s řetězcem délky K.
- Pro každé písmeno c nejvýše jedno volání s řetězcem sub(c). Všimněme si, že jelikož v pravidlech nejsou cykly, nikdy se nezavoláme dvakrát na sub(c) pro stejné c.
Pokud si označíme L celkovou délku všech nahrazovacích pravidel, bude časová složitost celého algoritmu O(K+L) – včetně předpočítání délek expanzí.
A protože zadání požaduje vypsání 10 číslic, prostě celý algoritmus spustíme desetkrát pro pozice P až P+9. To nám časovou složitost asymptoticky nezhorší.
 33-5-3 Těžký vozík (Zadání)
33-5-3 Těžký vozík (Zadání)
Uvážíme všechny možné kombinace polohy a rychlosti jako vrcholy grafu. Každý vrchol tedy reprezentuje možný stav vozíku před začátkem tahu.
Do tohoto grafu pak přidáme orientované hrany. Každá hrana bude reprezentovat přechod mezi stavy, který lze učinit pomocí jednoho tahu.
Z každého vrcholu tedy povede maximálně devět hran, protože v každém směru máme tři možnosti, jak rychlost vozíku změnit.
Pro každý vrchol zvládneme hrany z něho odcházející poměrně snadno spočítat. Pro každou možnou změnu rychlosti nejprve rychlost přepočítáme a novou polohu pak určíme jako součet rychlosti a polohy. Poté je nutné zkontrolovat, zdali nová poloha a rychlost skutečně odpovídají nějakému vrcholu, tedy jestli poloha leží v plánku a velikost rychlosti není příliš veliká (bude vysvětleno později). Zbývá tedy jen určit, zdali je tento čtverec volný, a tedy tato hrana je validní.
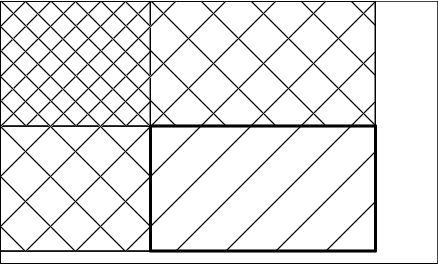
Toto můžeme kontrolovat pomocí dvojrozměrných prefixových součtů. To je datová struktura, která si pamatuje počet překážek pro všechny obdélníky s jedním rohem v levém horním rohu plánku a druhým rohem na jednom z políček. Pomocí nich lze pak zjišťovat počet překážek v libovolném obdélníku v konstantním čase. Stačí vhodně sčítat a odečítat počty překážek v předpočítaných obdélnících:
Když už máme graf vygenerovaný, požadovanou odpověď již zvládneme jednoduše zjistit pomocí průchodu do šířky. Jedná se totiž o vzdálenost vrcholů odpovídající políčkům začátku a konce s nulovou rychlostí.
Nyní pojďme omezit velikost grafu.
| (X-1)X |
| 2 |
| (X-1)X |
| 2 |
Počet vrcholů grafu tedy je O(NM√NM). Z toho nám vyplyne odhad paměťové i časové složitosti O(NM√NM).
 33-5-4 Nevěřící Bob (Zadání) (Komentáře)
33-5-4 Nevěřící Bob (Zadání) (Komentáře)
Různost prvků
Pokud chceme Boba přesvědčit o tom, že čísla x1,… ,xn jsou navzájem různá, stačí mu ukázat, jak je setřídit. Pošleme mu posloupnost indexů i1,… ,in takovou, že
Tento důkaz je velký O(n). V čase O(n) umíme zkontrolovat, že se v něm každý index od 1 do n vyskytuje právě jednou. Pak projdeme čísla v tomto pořadí indexů a ověříme, že jsou ostře rostoucí.
Nejkratší cesta
Nejprve předpokládejme, že žádná hrana grafu nemá nulovou délku. Pak jako důkaz stačí předložit vzdálenosti (délky nejkratších cest) od startu do všech ostatních vrcholů. Ukážeme, jak tento důkaz ověřit.
Označme d(v) vzdálenost od startu s do v uvedenou v důkazu a ℓ(u,v) délku hrany mezi u a v.
Nejprve zkontrolujeme, že důkaz je konzistentní s grafem. K tomu stačí ověřit následující podmínky:
- d(s) = 0
- Pro každý vrchol v≠ s existuje jeho soused u takový, že d(v) = d(u) + ℓ(u,v). Tomuto sousedovi říkáme předchůdce vrcholu v.
- Pro každou hranu {u,v} platí d(v) ≤ d(u) + ℓ(u,v). (Vlastně říkáme, že si žádnou hranou nelze zkrátit cestu. To je trojúhelníková nerovnost.)
Proč to stačí? Z prvních dvou podmínek plyne, že pokud z nějakého vrcholu v chodíme po předchůdcích, d(…) stále klesá, takže po konečném počtu kroků musíme dojít do s. Tím jsme sestrojili cestu z v do s, jejíž délky hran se sečtou na d(v). A je-li d(v) délkou nějaké cesty, nemůže být menší než délka nejkratší cesty. Jenže d(v) nemůže být ani větší – kdyby existovala nějaká kratší cesta než ta, kterou jsme sestrojili, na aspoň jedné její hraně by musela být porušena podmínka 3.
Pokud nám Alice kromě důkazu pošle i nejkratší cestu, umíme snadno ověřit, že je skutečně nejkratší. Stačí pro každou hranu {u,v} na cestě zkontrolovat, že d(v) = d(u) + ℓ(u,v).
Máme tedy důkaz velký O(n), který umíme zkontrolovat v čase O(n+m).
Zbývá dořešit, co si počít s hranami nulové délky. Předchozí důkazový systém pro ně nefunguje – chození po předchůdcích by mohlo skončit na nějakém cyklu z nulových hran a nikdy nedojít do s. Stačí ale provést jednoduchou transformaci: všechny délky hran vynásobíme n a přičteme k nim 1. Tím pádem se délky cest vynásobí n a přičte se počet hran na cestě. Nejkratší cesty stále zůstanou nejkratšími cestami (počet hran nikdy nedosáhne n, pročež se nejkratší a druhá nejkratší cesta nemohou prohodit). Tak jsme se zbavili nulových hran, a přesto stále umíme ověřit nejkratší cestu v původním grafu.
Editační vzdálenost
Editační vzdálenost převedeme na nejkratší cestu v grafu pomocí myšlenky z kuchařky o dynamickém programování.
Hledáme-li vzdálenost řetězce α délky a od řetězce β délky b, vytvoříme ohodnocený orientovaný graf, jehož vrcholy budou v ležet mřížce (a+1)×(b+1). Řádky budou indexované znaky prvního řetězce, sloupce znaky druhého řetězce.
Hrany budou odpovídat editačním operacím. Speciálně z vrcholu (i,j) povedou hrany:
- do (i+1,j) s délkou 1 – tato hrana odpovídá smazání znaku α[i]
- do (i,j+1) s délkou 1 – tato odpovídá vložení znaku β[i]
- do (i+1,j+1) s délkou 1 – změna znaku α[i] na β[j]
- do (i+1,j+1) s délkou 0, pokud α[i]=β[j] – znak necháme na pokoji
Stejně jako v kuchařce nahlédneme, že cesty z (0,0) do (n,m) odpovídají posloupnostem editačních operací, které z α udělají β. Navíc délka cesty je rovna počtu operací. Vzdálenost po nejkratší cestě tedy odpovídá editační vzdálenosti α od β.
Teď by stačilo použít náš důkazový systém pro nejkratší cesty (a rozmyslet si, že funguje i pro orientované grafy). Jenže ouha – graf je moc velký: má Θ(ab) vrcholů.
Zadání nám ale slibuje, že editační vzdálenost bude řádově menší než a a b. Nechť e je editační vzdálenost. V grafu tedy existuje cesta délky e z (0,0) do (a,b). Tato cesta ovšem nikde nemůže opustit pás okolo „diagonály“ (vrcholy (i,i)) široký e na každou stranu od diagonály. Všechny hrany, které se vzdalují od diagonály, mají délku 1, takže všechny vrcholy mimo pás jsou od (0,0) vzdálené víc než e.
Stačí tedy důkazový systém pro nejkratší cesty použít na tento pás, čímž jsme velikost důkazu snížili na Θ(ae). Čas potřebný na ověření důkazu bude také Θ(ae). (Divíte-li se, kam se podělo b, pak vězte, že a a b se mohou lišit nejvýš o e, takže Θ(ae) je totéž co Θ(be).)
 33-5-X1 (Zadání) (Komentáře)
33-5-X1 (Zadání) (Komentáře)
Právě jste vynalezli stroj času. Potřebujete se dostat do minulosti. Máte neodkladný úkol. Musíte říct svému mladšímu já něco důležitého – zadání této úlohy, aby ji mohlo řešit.
Váš stroj času je ovšem jenom prototyp a proto má nějaká omezení. Umí vás přenést pouze do určitého času – do února tohoto roku. Navíc vás nedoveze do vašeho domu, ale skončíte na druhé straně svého města. Z důvodu rušení je tu ještě jeden problém, můžete cestovat pouze v noci. V minulosti se samozřejmě nemůžete zdržovat moc dlouho, aby nevznikl nějaký zásadní paradox.
Z místa, kam vás stroj času přenese, se tedy budete muset dostat k sobě domů. Ovšem je tu problém. V době, kam se přenesete, platí přísná protiepidemická opatření (Nebo protiepidemiologická? Bylo to tehdy všechno nějaké zmatené…). Je tedy zakázáno pohybovat se v noci jen tak po městě. Na toto opatření samozřejmě dohlíží policie, se kterou se nechcete dostat do křížku, protože vysvětlit policistům, že cestujete v čase, není jednoduché.
Bohužel se vám nepodařilo zjistit, kde se v daný den nacházely policejní hlídky. Ovšem víte, že policajti nedělají žádnou práci zbytečně, takže ve městě bude rozmístěno co nejméně hlídek tak, aby každá křižovatka byla v dohledu alespoň jedné hlídky. Město si můžeme představit jako graf – křižovatky odpovídají vrcholům a ulice mezi nimi jsou hrany. Být v dohledu znamená, že se jedná o vrchol, v jehož sousedním vrcholu je hlídka.
Vašim úkolem tedy je zjistit, kde byly hlídky (můžete předpokládat, že existuje jediné minimální rozestavění), a pak naplánovat nejbezpečnější cestu domů. Chodit přes křižovatky, kde je hlídka, samozřejmě nemůžete. Také ale můžete být spatřeni hlídkou na sousední křižovatce. Nebezpečnost průchodu každou křižovatkou je tedy počet hlídek, které s ní sousedí. Vy pak chcete minimalizovat součet nebezpečností na křižovatkách po cestě.
Na vstupu dostanete popis města. Pro každý vrchol je tu jeden řádek začínající znakem označujícím daný vrchol následovaný dvojtečkou. Za ní jsou pak vypsány všechny sousední vrcholy dle pořadí, jak jdou ulice na dané křižovatce po sobě. Začínáte v prvním vrcholu a chcete se dostat do posledního.
Na výstup je potřeba vypsat několik řetězců oddělených bílými znaky. Nejprve
jako jedno slovo identifikátory všech vrcholů, kde budou hlídky, poté nebezpečnost
vaší trasy, dále pak vrchol, do kterého budete muset vyrazit ze startu, a nakonec
popis trasy. Pro každý vrchol trasy kromě startu a cíle vypište
řetězec znaků + nebo - reprezentující, jestli
máte dále vyrazit [počet mínusů]-tou ulicí doleva, nebo [počet plusů]-tou ulicí doprava
vůči ulici, kterou jste přišli.
Na každé křižovatce je nutné použít nejkratší možný zápis.
 33-5-S Globální iluminace a path tracing (Zadání)
33-5-S Globální iluminace a path tracing (Zadání)
Zde naleznete odkazy na referenční implementace úkolů ze všech dílů seriálu. Slovní popis řešení zde není, protože tím je vlastně samotný text seriálu.
První díl – Z hlubin fraktálů
- Úkoly 1, 2, 3 (pro zrcadlení viz řádek 28):
https://www.shadertoy.com/view/WstyRX - Úkol 4: https://www.shadertoy.com/view/3dtcRX
- Úkol 5: https://www.shadertoy.com/view/ws3BzH
Druhý díl – Šumy
- Úkol 1: https://www.shadertoy.com/view/WtdcDB
- Úkol 2: https://www.shadertoy.com/view/tttyWS
- Úkoly 3, 4: https://www.shadertoy.com/view/wtdyWS
- Úkol 5: https://www.shadertoy.com/view/tttcWS
Třetí díl – Světlo a stín
Úkol 2: https://www.shadertoy.com/view/WtyBDV
Vzorové řešení prvního úkolu je vlastně první půlka textu zadání, proto zde není.
Čtvrtý díl – Raytracing
- Úkoly 1–5: https://www.shadertoy.com/view/wdGBzV
- Úkol 5, alternativa s vícenásobnými odrazy:
https://www.shadertoy.com/view/NsfSzX - Úkol 6: https://www.shadertoy.com/view/fdfXRX
Pátý díl – Globální iluminace a path tracing
Všechny úkoly:
https://www.shadertoy.com/view/3ttfDr