Třetí série třicátého třetího ročníku KSP
Celý leták v PDF.
Dostává se k vám letošní vánoční vydání třetí série KSP-H 33. ročníku KSP.
Naleznete zde 4 normální úlohy, z toho jednu kompetitivní nad reálnými daty Prahy, bonusovou těžší úlohu a pak také pokračování seriálu o počítačové grafice. Všechny díly seriálu můžete odevzdávat v průběhu celého roku, takže vůbec nevadí, že jste třeba první díl nestihli. Detaily naleznete u zadání seriálu. Připomínáme, že oproti loňskému ročníku se do výsledkové listiny započítávají všechny úlohy mimo bonusové a body se již nepřepočítávají podle počtu vyřešených sérií.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (této kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, placku a možná i další překvapení.- Termín série: neděle 21. února 2021 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Třem nejúspěšnějším řešitelům kompetitivní úlohy pošleme sladkou odměnu.
Zadání úloh
- 33-3-1: Bezpečný tunel
- 33-3-2: Ospalý student a diktát
- 33-3-3: Stříbrných stříkaček
- 33-3-4: Obsazování území
- 33-3-S: Světlo a stín
- 33-3-X1: Z(a)tracené kouzlo
 33-3-1 Bezpečný tunel (9 bodů)
33-3-1 Bezpečný tunel (9 bodů)
Představme si svět zasažený vysoce nakažlivou nemocí. Aby lidé nebyli nakaženi, byla přijata přísná opatření proti šíření nemoci, mezi něž patří i omezení pohybu osob. Je zakázáno vzdalovat se více než 500 metrů od místa bydliště.
Kevin a Zuzka, jejichž domy jsou od sebe vzdáleny více než 1000 metrů, se ale nutně potřebují setkat. Naštěstí existuje způsob, jak se mohou i v tomto případě potkat, aniž by skončili ve vězení – mohou vykopat tajný tunel, který začíná a končí v oblasti, do které ještě mohou legálně dojít. V něm budou v bezpečí před policií i dalšími nezvanými hosty. Kopání tunelu je ale náročná věc, proto by chtěli, aby byl co nejkratší.
Máte zadáno město velikosti M ×N jako bludiště ve čtvercové síti. Jednotkou je 1 metr, každá buňka je buď průchozí nebo je na ní zeď. V bludišti máte dva body A a B, což jsou pozice domů Kevina a Zuzky.
Od bodů A, B se smíte vzdálit maximálně na K=500 metrů. Vzdálenosti se měří Manhattanskou metrikou, takže vzdálenost v dvou bodů p=[x1, y1] a q=[x2, y2] je definována jako v =|x1 - x2| + |y1 - y2|. Při průchodu městem se nesmíte v žádné chvíli vzdálit na víc než K metrů od A nebo B (není povoleno projít cestou, jejíž část prochází oblastí vzdálenou více než K, i kdyby se cesta poté zase vrátila do legální oblasti).
Chceme najít co nejkratší tunel, který má konce na pozicích TA a TB. K bodu TA musí vést cesta z A, která se od A nikdy nevzdálí na víc než K metrů. To samé platí i pro TB a bod B. Tunel je pod zemí, takže není nijak omezen zdmi v bludišti (podkope se pod nimi).
Od vás chceme vymyslet algoritmus na hledání tohoto nejkratšího tunelu. Dostane na vstupu zadanou mapu města a pozice domů A a B a najde nejkratší tunel.
 33-3-2 Ospalý student a diktát (10 bodů)
33-3-2 Ospalý student a diktát (10 bodů)
Kevin včera do noci řešil KSP a na hodině matematiky se mu nedaří udržet pozornost. Učitel se mu opakovaně snaží nadiktovat posloupnost různých čísel (zadání domácího úkolu), ale Kevin vždy zachytí pouze útržky. Učitele to po několika pokusech přestane bavit a pokračuje ve výkladu.
Po návratu domů (a pořádném šlofíku) se Kevin dívá do sešitu, kde má několikrát napsané části domácího úkolu a zajímá ho, zda z nich je možné jednoznačně sestavit úkol celý. Délku posloupnosti si naštěstí zapamatoval.
Pro délku úkolu 4 a útržky (2, 3, 5), (2, 1) a (1, 3) jde jednoznačně sestavit posloupnost (2, 1, 3, 5). Pro (2, 3, 5) a (1, 3) již posloupnost jednoznačně sestavit nejde, protože pořadí 1 a 2 není jasně určeno. Pro (2, 1, 3, 5) a (3, 2) posloupnost sestavit také nejde, protože pořadí 2 a 3 neodpovídá (při diktování se musela stát chyba).
Znáte délku výsledné posloupnosti a útržky. Pomozte Kevinovi určit, zda jde posloupnost z útržků jednoznačně sestavit. Pokud nejde, určete proč.
 33-3-3 Stříbrných stříkaček (13 bodů)
33-3-3 Stříbrných stříkaček (13 bodů)

Přes výstupní kontrolu chodí různé modely stříbrných stříkaček. Víme, že každý model má jiný dostřik (vyjádřený celým číslem).
U každé stříkačky bychom rádi ihned věděli, kolik modelů s menším dostřikem již výstupní kontrolou prošlo.
Nyní si můžete rozmyslet, jak tuto úlohu vyřešit. To po vás ale tentokrát nebudeme chtít.
Vašek si na to napsal následující program s pomocí treapů, o kterém si myslel, že za jakýchkoliv okolností bude fungovat opravdu rychle. Doufal, že na každý dotaz odpoví v logaritmickém čase vzhledem k počtu předešlých dotazů.
from random import randint
class Node:
left = None
right = None
def __init__(self, priority, key):
self.priority = priority
self.key = key
self.size = 1
def update(node):
if node is None:
return
node.size = 1
if node.left is not None:
node.size += node.left.size
if node.right is not None:
node.size += node.right.size
def merge(left, right):
if left is None or right is None:
return left if right is None else right
if left.priority < right.priority:
left.right = merge(left.right, right)
update(left)
return left
else:
right.left = merge(left, right.left)
update(right)
return right
def split(parent, key):
if parent is None:
return (None, None)
left = right = None
if parent.key < key:
left = parent
left.right, right = split(parent.right, key)
else:
right = parent
left, right.left = split(parent.left, key)
update(left)
update(right)
return (left, right)
n = int(input())
root_node = None
for i in range(n):
_input = int(input())
a, root_node = split(root_node, _input)
root_node, b = split(root_node, _input + 1)
if root_node is None:
root_node = Node(randint(0, 10**9), _input)
root_node = merge(merge(a, root_node), b)
#include<bits/stdc++.h>
using namespace std;
int random_number()
{
return rand();
}
struct Treap
{
Treap *left=NULL, *right=NULL;
int key, priority;
int size=1;
};
void update(Treap *in)
{
if (!in) return;
in->size = 1;
if (in->left) in->size += in->left->size;
if (in->right) in->size += in->right->size;
}
Treap *merge(Treap *left, Treap *right)
{
if (!left || !right) return left?left:right;
if (left->priority < right->priority)
{
left->right = merge(left->right, right);
update(left);
return left;
}
else
{
right->left = merge(left, right->left);
update(right);
return right;
}
}
pair<Treap*, Treap*> split(Treap *in, int key)
{
Treap *left=in, *right=in;
if (!in) return {NULL, NULL};
if (in->key < key)
tie(left->right, right) =
split(in->right, key);
else
tie(left, right->left) =
split(in->left, key);
update(left);
update(right);
return {left, right};
}
Treap *treap;
int main()
{
int n;
scanf("%d",&n);
for (int i=0;i<n;i++)
{
int input;
scanf("%d",&input);
Treap *a, *b;
tie(a,treap) = split(treap,input);
tie(treap,b) = split(treap,input+1);
printf("%d\n",a?a->size:0);
if (!treap)
{
treap = new Treap;
treap->priority = random_number();
treap->key = input;
}
treap = merge(merge(a,treap),b);
}
return 0;
}
Ukažte mu, že se může stát, že jeho algoritmus nebude tak rychlý,
jak čekal. Vaším úkolem bude nalézt vstup, na kterém tento algoritmus poběží
pomalu. Konkrétně Vaškovo řešení musí alespoň M krát spustit funkci
merge nebo split (číslo M dostanete na vstupu).
Abyste mohli takový vstup vyrobit, tak budete potřebovat čísla z náhodného
generátoru. Podařilo se vám zjistit, jaké hodnoty bude postupně po spuštění
vracet funkce random_number(). Vašim úkolem bude vytvořit pořadí
stříbrných stříkaček na vstupu.
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na vstupu dostanete na prvním řádku čísla N a M. Číslo N udává počet náhodných čísel, které se vám povedlo zjistit, a zároveň limituje maximální počet stříbrných stříkaček. Číslo M je minimální počet operací, které musí odevzdaná posloupnost stříbrných stříkaček vygenerovat. Na dalších N řádcích jsou pak zjištěná náhodná čísla z náhodného generátoru v rozsahu mezi nulou a 106.
Pro jednotlivé vstupy platí:
| Vstup | N | M |
| 1. | 3 | 20 |
| 2. | 1 000 | 490 000 |
| 3. | 1 000 | 490 000 |
| 4. | 2 000 | 2 000 000 |
Formát výstupu: Na první řádek výstupu nejprve vypište X≤ N – počet stříbrných stříkaček, které chcete předhodit programu na vstupu. Na následujících X řádcích pak vypište jednotlivá čísla. Každé z nich musí být celé číslo mezi 0 a 109
3 10 123 321 222
2 1 2

 33-3-4 Obsazování území (14 bodů)
33-3-4 Obsazování území (14 bodů)
Během některých období řádění vysoce nakažlivé nemoci rozhodli vládci jednoho fiktivního království, říkejme mu třeba Fiktivní Praha, že se nikdo nesmí pohybovat dále, než 500 metrů od svého domu.
Ve Fiktivní Praze se vyskytoval i fiktivní Kevin a toho napadlo, že kdyby si koupil více domů, mohl by se procházet po větší části města. Začal svoji myšlenku rozvíjet dál a napadlo ho, že kdyby si koupil dostatečné množství domů, mohl by se procházet po celé Fiktivní Praze. Zajímalo by ho ale, kolik nejméně bude muset utratit, aby svého cíle dosáhl.
Fiktivní Praha se rozkládá na čtverečkové síti o rozměrech 214 ×214 (neboli 16 384 ×16 384) políček. Některá políčka obsahují domy a dají se za nějakou cenu koupit (každé políčko se dá koupit samostatně bez ohledu na to, jestli patří do nějaké budovy rozkládací se přes více políček). Mapu Fiktivní Prahy můžete vidět na následujícím obrázku – ale nebojte se, data vám naservírujeme i v jednodušší podobě.

Mapu si také můžete stáhnout (třeba jako obrázek na pozadí):
Pokud někdo vlastní budovu na políčku [x,y], tak se může volně pohybovat na políčkách od [x-500,y-500] až po [x+500, y+500] včetně (mohli bychom říci, že může do vzdálenosti 500 od [x,y] v maximové metrice).
Fiktivní Kevin by chtěl mít „zpřístupněná“ všechna zastavěná políčka, ale chtěl by za to utratit co nejméně. Vaším úkolem bude najít množinu políček, na nichž stojí domy a jejichž nákupem se zpřístupní všechna ostatní zastavěná políčka v mapě. Z takových množin políček se budete pokoušet najít tu, za kterou utratíte co možná nejméně (tedy budete minimalizovat součet cen vybraných políček).
Toto je speciální kompetitivní úloha se statických vstupem. Všichni řešitelé dostanou stejný vstup a přes Odevzdávátko pak odevzdají nejlepší řešení, které se jim povede najít. Obodování úlohy provedeme až po konci série a to tak, že nejlepší řešení dostane plný počet bodů a ostatní řešení dostanou body odstupňovaně podle toho, jak byla dobrá. Zároveň slibujeme, že každé korektní řešení (zpřístupňující všechna zastavěná políčka) dostane alespoň jeden bod.
V průběhu série se můžete s ostatními porovnávat pomocí průběžné online výsledkovky – upozorňujeme, že se v ní mohou vyskytnout i řešení od organizátorů.
Formát vstupu: Vstup je statický a stačí si ho stáhnout jen jednou. Je
tvořen mapou cen v binárním souboru, který se sestává ze 16 384 ×16 384
dvoubajtových čísel bez znaménka (Cčkový datový typ uint16_t) zapsaných
v little-endian formátu (méně významný bajt první a více významný bajt
druhý). Data jsou uvedeny po řádcích a začínají v levém vrchním rohu mapy.
S načtením vám mohou pomoci ukázky kódu níže.
Načtená čísla udávají cenu každého políčka (v korunách za metr čtvereční stavební parcely). V případě, že je číslo nula, tak se nejedná o zastavěné políčko (a není ho nutné zpřístupňovat, jedná se například o řeku nebo pole).
#include <stdint.h>
#include <stdlib.h>
#include <stdio.h>
#define S 16384
// Funkce na převod little-endian uint16_t do endianity procesoru (ať je jakákoliv)
uint16_t le16_to_cpu(const uint8_t *buf) {
return ((uint16_t)buf[0]) | (((uint16_t)buf[1]) << 8);
}
int main() {
uint8_t *buffer = malloc(S*S*2);
if (buffer == NULL) die("Nelze alokovat");
fread(buffer, sizeof(uint8_t), S*S*2, stdin);
uint16_t **mapa = malloc(sizeof(uint16_t*)*S);
for (int r = 0; r < S; r++) {
// Použijeme trik, kdy mapa bude bydlet v prostoru alokovaném pro buffer, jenom
// každé číslo převedeme funkcí, která zajistí správnou endianitu
mapa[r] = (uint16_t*)&buffer[2*r*S];
for (int s = 0; s < S; s++)
mapa[r][s] = le16_to_cpu(&buffer[2*r*S + 2*s]);
}
}
import sys
import numpy
from array import array
S = 16384
mapa = []
for y in range(S):
# Musíme dát pozor na endianitu (data jsou
# little-endian) a tak načtení svěříme numpy
numpy_radek = numpy.fromfile(
sys.stdin.buffer,
dtype="<u2", # unsigned 2bajtová čísla
count=S # v little-endian(<)
)
# Pro rychlejší přístup k prvkům převedeme
# na interní Pythoní pole
radek = array('H') # minimálně 2b číslo
radek.fromlist(numpy_radek.tolist())
mapa.append(radek)
Formát výstupu: Výstup bude mít textový formát. Na první řádek výstupu uveďte počet domů, které kupujete, a na další řádky uveďte souřadnice zakoupených domu, na každý řádek jeden dům. Souřadnice uveďte jako číslo řádku a pak číslo sloupce oddělené mezerou (oboje indexujeme od nuly a bod [0,0] je levé vrchní políčko).
Maximální počet odevzdaných domů je 10 000 (do toho by se všechna rozumná řešení měla vejít).
Odevzdávátko spočítá cenu za nakoupené domy a přidá odevzdané řešení do průběžné výsledkovky. Upozorňujeme, že od každého řešitele bereme v potaz vždy jeho poslední odevzdané řešení, i kdyby si tím měl zhoršit skóre. Proto vám doporučujeme si své řešení ukládat, abyste je případně mohli odevzdat znovu.
Zdroje: Mapu s cenami k této úloze jsme získali zpracováním dat OpenStreetMap (pozice domů na mapě) a také otevřených datových sad poskytovaných Hlavním městem Prahou (ceny za dům v jednotlivých oblastech).
 33-3-X1 Z(a)tracené kouzlo (10 bodů)
33-3-X1 Z(a)tracené kouzlo (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Kouzelník Magiáš už několik hodin soustředěně hryže špičku kouzelnické hůlky. Rád by nabubřelému starostovi sousední vsi přičaroval oslí uši – to vždycky byla taková zábava! – jenže se mu nedaří vzpomenout si na správné zaklínadlo. Takhle přikouzlí oslí uši nanejvýš svým grimoárům.

Ale co už, kde nepomůže paměť, pomůže technika. Magiáš si je jistý, že kdyby zaklínadlo viděl, okamžitě ho pozná. Vytahuje tedy z truhlice počítač, pořádně zatočil klikou a vygeneroval náhodnou posloupnost znaků. Jestlipak v ní najde, co hledal?
Vymyslete algoritmus, který dostane nějakou abecedu (konečnou množinu obsahující A znaků), zaklínadlo (řetězec délky Z tvořený znaky abecedy) a číslo N. Výstupem algoritmu bude počet řetězců o N znacích abecedy, které obsahují zaklínadlo jako souvislý podřetězec. Jelikož výsledek může být obrovské číslo, počítejte modulo nějaké velké prvočíslo P.
Můžete předpokládat, že N je mnohem větší než Z a A.
Příklad: Uvažujme abecedu { A, B, C }.
Všech řetězců délky N=5 existuje 35 = 243.
Zaklínadlo ABC se vyskytuje ve 27 z nich,
zaklínadlo AAA jen ve 21.
 33-3-S Světlo a stín (14 bodů)
33-3-S Světlo a stín (14 bodů)
Toto je seriálová úloha, která navazuje na podobné úlohy v minulých sériích. Pokud jste předchozí díly seriálu neřešili, pro pochopení tohoto dílu je dobré si jej nejméně přečíst. A pokud si chcete úlohy z minulých dílů také naprogramovat, stále za ně můžete získat polovinu bodů.
Minule jsme si pořídili několik šumových funkcí. Nyní se podíváme, jak se z nich dá poskládat konkrétní povrch. Barva povrchu samotná ale není tolik zajímavá, proto zároveň s ní vygenerujeme i výškovou mapu povrchu, který definuje jeho tvar. Bude se nám hodit, až se naučíme simulovat chování světla a nějak zajímavě povrch osvětlíme. Nejdříve ale musíme mít co osvětlovat.
V tomto díle vás čekají jen dva úkoly. Prvním je udělat nějaký proceduální obraz nebo povrch, druhým je implementovat Phongův osvětlovací model. Jako návod pro první úkol je zde popis, jak udělat proceduální cihlovou zeď, po něm následuje teorie o světle a nakonec zadání druhého úkolu.
Proceduálně generovaný obraz
Úkol 1 [6b]
Vytvořte v Shadertoy nějaký libovolný, zajímavý, proceduálně generovaný obraz. Může být i animovaný. Mlhovina, vodní hladina, nějaký zajímavý vzor…
Pravděpodobně se vám budou hodit šumové funkce z minulého dílu seriálu. Mnoho inspirace a návodů naleznete v The Book of Shaders. Fantazii se meze nekladou. Nemusí se jednat o nic složitého, ale mělo by to být něco více než zkopírovaný kód ze seriálu nebo jiných zdrojů.
Též můžete vytvořit něco napodobující realistický povrch. Níže najdete právě příklad toho, jak ze šumů poskládat cihlovou zeď. Nemusí to být tak komplikované jako tento příklad (určitě nedělejte nic složitějšího) a můžete využívat kousky kódu ze seriálu. Pokud se vydáte touto cestou, soustřeďte se i na výšku povrchu, později ji využijeme.
Také vězte, že za vytvořením čehokoliv ze šumů se neskrývá žádný pevný postup, spíše se věci hackují dokud nevypadají tak jak mají. Příklad cihlové zdi níže je zde jako návod a inspirace.
A pokud se vám editor seká, zapausujte si překreslování obrazu tlačítkem
v levém dolním rohu. Obraz se stále obnoví, pokud někam kliknete myší nebo
překompilujete shader (na což se hodí klávesová zkratka alt+enter).
Bodování (celkem 6 bodů):
- základ 4 body za netriviální funkční obraz
- pokud se rozhodnete dělat povrch, +2 body za smysluplnou výškovou mapu
- pokud se rozhodnete dělat něco jiného, +2 body za smysluplnou animaci
Zde je pár nápadů na povrch:



Od šumů k povrchu
Pokusíme se vytvořit funkci napodobující cihlovou zeď:

Začneme nejnápadnější strukturou v tomto povrchu: obdélníkovými cihlami. Obdélník není nic jiného než protáhlý čtverec, a jak si možná pamatujete z minulého dílu, se čtvercovými buňkami jsme se už setkali (u Perlinova šumu):
vec4 brick(vec2 uv)
{
// Souřadnice v rámci buňky
vec2 f = fract(uv);
float height = max(f.x, f.y);
return vec4(0.0, 0.0, 0.0, height);
}
void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
vec2 uv = fragCoord/iResolution.xy;
// Převedeme uv do rozsahu -1..1
uv = uv * 2.0 - 1.0;
// "Natáhneme" X tak, aby byl zachován poměr stran
uv.x *= iResolution.x / iResolution.y;
// Nyní je tedy čtverec v souřadnicích i čtvercem na monitoru
vec4 surface = brick(uv);
fragColor = vec4(surface.www, 1.0);
}
Funkce brick zatím tvoří jen jakési čtvercové artefakty. Všimněte si, že
tato funkce nevrací jen barvu povrchu v daném bodě, nýbrž i jeho výšku (jako
komponentu w výsledného vektoru). Zatím na monitor zobrazujeme jen tuto
výšku. Tmavé (malé) hodnoty výšky jsou dál od pozorovatele (hlouběji v povrchu),
světlé jsou blíže. Výška se nám bude hodit, až budeme povrch osvětlovat.
Na povrchu chceme nějak zvýraznit okraje „cihlových“ buněk, kde bude vidět malta.
vec4 brick(vec2 uv)
{
// Souřadnice v rámci buňky
vec2 f = fract(uv);
// Převedeme je do rozsahu -1..1
f = f * 2.0 - 1.0;
f = abs(f);
float height = max(f.x, f.y);
return vec4(0.0, 0.0, 0.0, height);
}
Tím, že jsme převedli f (tedy souřadnice uvnitř buňky) do rozsahu -1 až 1,
tak platí, že u kraje buňky je aspoň jedna ze souřadnic v absolutní hodnotě
blízko jedničce. Výšku získáme tím, že z absolutních hodnot x a y složek
f vezmeme maximum.
Hodnotu f nyní nějak upravíme tak, aby výsledek vypadal trochu blíž tvaru
cihel v předloze. Výšku invertujeme, aby platilo, že malta je hlouběji
v povrchu.
vec4 brick(vec2 uv)
{
// Souřadnice v rámci buňky
vec2 f = fract(uv);
// Převedeme je do rozsahu -1..1
f = f * 2.0 - 1.0;
f = abs(f);
float height = max(f.x, f.y);
height = max((height - 0.75) * 4.0, 0.0);
height = pow(height, 3.0) * 3.0;
height = 1.0 - clamp(height, 0.0, 1.0);
return vec4(0.0, 0.0, 0.0, height);
}
Umocnění na třetí má za následek ostřejší přechod mezi černou a bílou.
Násobení 4.0 a odečtení 0.75 zařídí, aby hodnoty z max(f.x, f.y) byly po tři čtvrtě
vnitřku cihly rovny nule a až v poslední čtvrtině narostly do jedničky.
Jinak by se celý vnitřek cihly ostře svažoval k okrajům (schválně to zkuste),
takto je většina svahu „useklá“ tím, že jsme ji přesunuli do záporných
hodnot. Poslední násobení třemi ovládá šířku okraje cihel.
Zatím vidíme jen dvě řady cihel, chceme jich ale mít v rozsahu -1 až 1 více.
Proto vstupní uv něčím vynásobíme. Všimněte si, že x-ovou komponentu uv
násobíme menší hodnotou než y-ovou, tím cihly protáhneme podle x.
Též chceme každou druhou řadu cihel posunout, k čemuž použijeme už spočítané
celočíselné souřadnice buňky v proměnné cell. Výsledný kód vypadá takto:
Také jsme si pro transformované souřadnice cihly zavedli proměnnou
brickuv, jejíž celá část identifikuje
cihlu a desetinná souřadnice uvnitř cihly. Původní netransformované uv
se nám totiž bude později hodit.
vec4 brick(vec2 uv)
{
// Chceme vidět v rozsahu -1..1
// více řad cihel, navíc cheme,
// aby byly cihly obdélníkové
vec2 brickuv = uv * vec2(2.0, 4.0);
int row = int(floor(brickuv.y));
// Každou druhou řadu cihel posuneme
if((row & 1) == 0)
brickuv.x += 0.5;
// Souřadnice v rámci buňky
vec2 f = fract(brickuv);
// Převedeme je do rozsahu -1..1
f = f * 2.0 - 1.0;
f = abs(f);
float height = max(f.x, f.y);
height = max((height - 0.75) * 4.0, 0.0);
height = pow(height, 3.0) * 3.0;
height = 1.0 - clamp(height, 0.0, 1.0);
return vec4(0.0, 0.0, 0.0, height);
}
Výraz (row & 1) je bitový AND, který vrací jedničku právě když má
row nastavený nejnižší bit. V podmínce tedy posune každý sudý řádek.

Nyní do tvaru cihel přidáme trochu chaosu. Použijeme k tomu fractal brownian motion z minulého dílu:
vec2 random2(vec2 st)
{
vec2 s = vec2(
dot(st, vec2(12.3456, 34.1415)),
dot(st, vec2(42.2154, 15.2854))
);
return fract(sin(s) * 45678.9) * 2.0 - 1.0;
}
float gradientNoise(vec2 st)
{
vec2 cell = floor(st);
vec2 f = fract(st);
vec2 s00 = random2(cell);
vec2 s01 = random2(cell + vec2(0, 1));
vec2 s10 = random2(cell + vec2(1, 0));
vec2 s11 = random2(cell + vec2(1, 1));
float d00 = dot(s00, f);
float d01 = dot(s01, f - vec2(0, 1));
float d10 = dot(s10, f - vec2(1, 0));
float d11 = dot(s11, f - vec2(1, 1));
vec2 u = smoothstep(0.0, 1.0, f);
float noise = mix(
mix(d00, d10, u.x),
mix(d01, d11, u.x),
u.y
);
return noise * 0.5 + 0.5;
}
float fbm(vec2 st)
{
float val = 0.0;
float p = 0.5;
const float angle = 1.0;
mat2 rotation = mat2(
cos(angle), sin(angle),
-sin(angle), cos(angle)
);
for (int i = 0; i < 5; i++)
{
val += gradientNoise(st) * p;
p *= 0.5;
st *= 2.0;
st += vec2(1.181, 0.57);
st = rotation * st;
}
return val;
}
vec4 brick(vec2 uv)
{
// Chceme vidět v rozsahu -1..1
// více řad cihel, navíc cheme,
// aby byly cihly obdélníkové
vec2 brickuv = uv * vec2(2.0, 4.0);
int row = int(floor(brickuv.y));
// Každou druhou řadu cihel posuneme
if((row & 1) == 0)
brickuv.x += 0.5;
vec2 f = fract(brickuv);
// Převedeme je do rozsahu -1..1
f = f * 2.0 - 1.0;
// Souřadnice, ze kterých bereme šum
// pro cihly, jsou různé pro každou buňku
vec2 noiseuv = brickuv * 2.0
+ floor(brickuv) * 42.2;
// Náhodný šum převedený do rozsahu -1..1
vec2 noise = vec2(
fbm(noiseuv),
fbm(noiseuv + vec2(12.244, 321.25))
) * 2.0 - 1.0;
f = abs(f + noise * 0.25);
float height = max(f.x, f.y);
height = max((height - 0.75) * 4.0, 0.0);
height = pow(height, 3.0) * 3.0;
height = 1.0 - clamp(height, 0.0, 1.0);
// Šum pro maltu v rozsahu 0..1
// Používáme původní uv, nikoliv brickuv
float backgroundNoise = fbm(uv * 64.0);
height = clamp(
height + backgroundNoise * 0.25,
0.0, 1.0);
// Šum pro cihly v rozsahu 0..1
float foregroundNoise = fbm(uv * 16.0);
// Šum umocníme na druhou
foregroundNoise *= foregroundNoise;
height = clamp(height
- height * (foregroundNoise)* 0.5,
0.0, 1.0);
return vec4(0.0, 0.0, 0.0, height);
}
Šum spočítáme dvakrát, jednou pro x a jednou pro y. Aby byly tyto hodnoty různé,
u y ke vstupu `fbm` přidáme nějaké posunutí. Tento dvojrozměrný
výsledek prostě přičteme k souřadnicím, ze kterých počítáme tvar cihly, čímž
ho zkreslíme. Též si všimněte, že k souřadnicím, ze kterých šum počítáme,
přičítáme floor(uv) * 42.2. Tato hodnota je vždy v rámci jedné cihly stejná,
pro sousední cihly se ale bude velmi lišit. Tím zajistíme, že sousední cihly
budou zkresleny různě (zkuste se podívat, jak by povrch vypadal, kdybychom to
nedělali).
Též zaneseme nějaký šum do nízkých míst (malta) a nějaký šum o jiné frekvenci přidáme i do cihel.
Jako poslední úpravu přidáme povrchu barvu. Malta na pozadí bude jednolitě šedá, cihly budou mít různé odstíny červené, opět získané náhodnou funkcí, která bude různá pro každou cihlu.
vec4 brick(vec2 uv)
{
// ...
// Výsledek obarvíme
vec3 color = vec3(0.4);
vec3 brickColor = vec3(0.8, 0.55, 0.5)
+ vec3(random2(floor(brickuv)), 0.0)
* vec3(0.15, 0.075, 0.0);
color = mix(color, brickColor, height);
return vec4(color, height);
}
void mainImage(out vec4 fragColor,
in vec2 fragCoord)
{
// ...
// Nyní už barevný výstup
fragColor = vec4(surface.rgb, 1.0);
}
A nyní, když už máme realistický povrch, tak bychom ho mohli i realisticky osvětlit!
Světlo
Simulace světla je asi největší část počítačové grafiky a budeme se jí věnovat téměř celý zbytek seriálu.
Světlo je, aspoň pro naše účely, proud nekonečně malých částic - fotonů. Každý foton má svou vlnovou délku, která určuje jeho barvu. Například vlnová délka 440nm odpovídá modré a 650nm červené. Intenzita světla je určena množstvím fotonů. V realtime vykreslování (což je vykreslování dost rychlé na to, aby bylo interaktivní, například pro hry) vlnovou délku fotonů víceméně ignorujeme a místo toho počítáme intenzitu světla „natřikrát“, jednou pro červenou, zelenou a modrou barvu. Ostatní barvy vytvoříme kombinací těchto tří, stejně jako to dělají monitory.
Tím přijdeme o některé jevy, například žlutý povrch, který odráží červené a zelené světlo se někdy chová viditelně jinak než žlutý povrch, který odráží žluté světlo. Běžně ale moc nenarazíme na situace, kde to má vliv.
Globální iluminace
Když vidíme nějaký objekt, tak to co vnímáme je světlo, které z jeho povrchu doputovalo do našich očí. Většina věcí sama viditelné světlo nevyzařuje a co vidíme je tedy světlo, které k danému povrchu doputovalo odjinud a odrazilo se směrem k nám. Tedy tím, že na nějaký povrch dopadá světlo, se tento povrch sám stává jakýmsi zdrojem světla a toto světlo se může dále odrážet od jiných objektů.
Představte si, že jste v noci v pokoji, kde je jediným zdrojem světla žárovka. I v místech, která jsou ve stínu, je něco vidět, přestože sem nedopadá světlo z žárovky přímo. Dopadá sem ovšem světlo odražené od těch částí místnosti, které ve stínu nejsou (a proto je tak častá bílá omítka na zdech – lépe odráží světlo a v místnosti je díky tomu lépe vidět).
Tomuto světlu, které k povrchu nedoputovalo přímo, ale nějak se po cestě odráželo od zbytku scény (v kontextu vykreslování se prostředí, které vykreslujeme, typicky říká scéna), se říká nepřímé světlo (anglicky indirect light). Naopak tomu světlu, které ze zdroje (žárovka, slunce) doputovalo na povrch přímo se říká přímé světlo (direct light).
Někdy se tomuto jevu, kdy se každá část scény stáva zdrojem světla, také říká globální iluminace. Pokud ale nějaká hra nebo engine tvrdí, že umí globální iluminaci, většinou mají na mysli simulaci nepřímého světla vzniklého aspoň jedním difúzním odrazem (viz níže).
Nepřímé světlo je pro vzhled vykreslované scény nesmírně důležité. Nicméně je také nesmírně náročné jej simulovat. První pokusy o realtime globální iluminaci ve hrách se začaly objevovat teprve během posledních pár let a jejich plného nasazení se nejspíše dočkáme až s právě přicházející generací silnějšího hardwaru. Doteď se používala buď globální iluminace předpočítaná, nebo triky, které také později použijeme.
Odrazy
Co se stane, když světlo dopadne na nějaký povrch?
Většina světla se zlomí dovnitř povrchu, kde se bude chaoticky odrážet a rozptylovat od atomů či molekul materiálu. Část z tohoto světla materiál absorbuje, zbytek světla jej opět opustí, ovšem díky své chaotické cestě skrz materiál bude toto světlo vyzářeno do všech směrů rovnoměrně. Tomuto světlu se anglicky říká diffuse light, můžete se potkat i s pojmenováním jevu difúzní odrazy nebo difúzní rozptyl světla. Typicky jsou různé vlnové délky světla absorbovány různě, čímž se difúzní světlo viditelně zabarví.
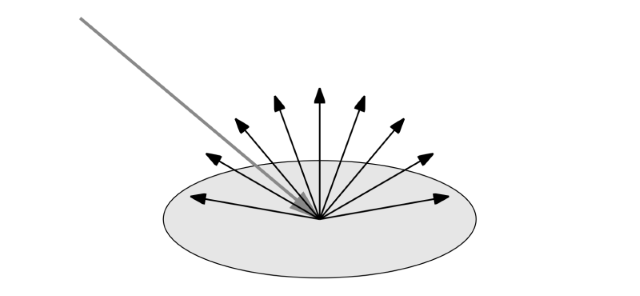
Může se stát, že nezanedbatelná část světla materiál opustí viditelně jinde, než kde do něj vstoupilo (pokud je materiál tenký, tak třeba i na jeho opačné straně). Tomuto jevu se říká subsurface scattering a je patrný například na slunci svítícím skrz listí nebo na lidské kůži. Pro většinu materiálů jej ale lze zanedbat.
Část světla se do povrchu nezlomí a místo toho se od něj „zrcadlově“ odrazí. Tomuto světlu se říká specular light, odrazům se říká spekulární odrazy. Toto světlo nebývá zabarvené, protože s materiálem skoro neinteragovalo. Ovšem pro kovy může být takto odražena téměř všechna příchozí energie, navíc kovy, na rozdíl od většiny nevodivých materiálů, mají tendenci odražené světlo silně zabarvovat (a tím se liší banán od zlata, přestože oba materiály jsou „žluté“).
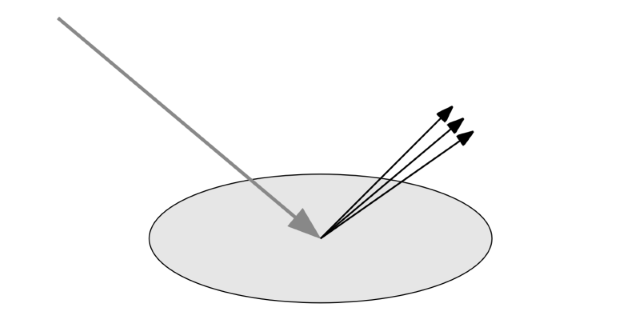
Na vzhled materiálu má vliv i jeho mikroskopický tvar. Především spekulární odrazy jsou jím velmi ovlivněny – hladké povrchy se lesknou jako zrcadlo, hrubé povrchy jsou matné.
Chování světla na povrchu je ovlivněno ještě mnoha dalšími parametry. Například na jinak hrubém povrchu může být tenká vrstva hladkého laku, která mění, jak budou vypadat odrazy. Také tvar mikroskopických nerovností má velký vliv na vzhled, zvlášť pokud jsou pravidelné, jako třeba na gramofonové desce nebo na DVD.
Parametry, kterými budeme popisovat materiál, se dají shrnout takto:
- difúzní barva – též intenzita difúzního světla, pro kovy slabá
- spekulární barva – pro nekovy bílá a slabá, pro kovy zabarvená a silná
- hrubost – ovlivňuje ostrost či matnost odrazů
Barvou v tomto případě myslíme jak odstín, tak světlost (tedy sílu odrazů). Větší hodnoty budou odrážet více světla.
Například Unreal Engine používá (mimo mnohé jiné) parametry base color a metallic, čili nějakou základní barvu a jednorozměrnou „kovovost“, ze kterých difúzní a spekulární barvu sám odvodí.
Lambertův zákon
Dřív, než začneme počítat, kolik světla se odrazilo z povrchu do našich očí (či spíše do naší virtuální kamery), je třeba zjistit, kolik světla na povrch dopadá. Sice počítáme osvětlení v nekonečně malém bodě, ale nyní si představme, že tento bod je ve skutečnosti malá ploška nějaké pevně dané velikosti, a víme, kolik světla by v tomto místě dopadlo na plochu stejného obsahu. Energie, která na tuto plošku skutečně dopadne, se ale bude výrazně lišit podle toho, jak je ploška orientovaná vzhledem ke zdroji světla.
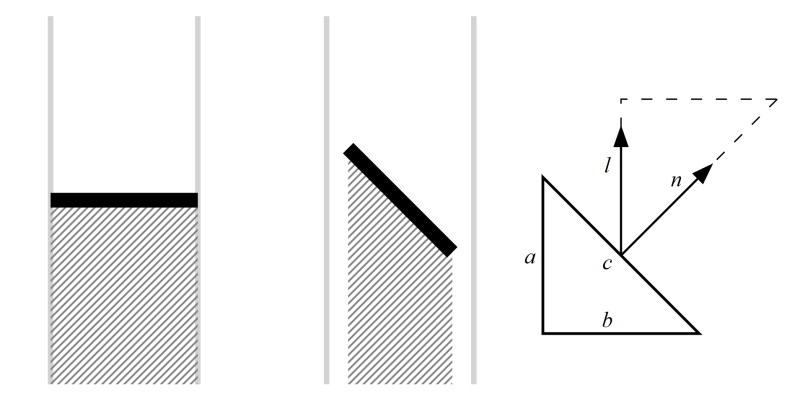
Jak je vidět z obrázku, tak když je ploška orientovaná kolmo na příchozí paprsky světla, dopadá na ni všechna energie, ale pokud je nějak natočená, dopadá na ni jen část energie a zbytek ji mine. Tato část energie je navíc přímo úměrná šířce „stínu“ plošky – čím širší stín, tím víc fotonů narazilo do plošky.
Poměr zachycené energie je tedy rovný poměru mezi velikostí plošky a velikostí stínu, v trojúhelníku toto odpovídá poměru stran b/c, tedy kosinu úhlu mezi těmito stranami. Tento úhel nalezneme též mezi zvýrazněnými vektory n a l (všimněte si, že dohromady tvoří trojúhelník podobný hlavnímu abc), kde n je vektor kolmý na plošku a l je vektor směřující ke světlu. Tomuto vztahu se říká Lambertův zákon, a toto je vše co potřebujeme pro spočítání (aspoň přibližného) difúzního osvětlení.
Spekulární odraz je složitější a existuje mnoho způsobů jak ho spočítat. My použijeme Phongův osvětlovací model. Je rychlý a jednoduchý, ale není nijak založený na fyzice světla, je navržen prostě tak, aby vypadal víceméně přirozeně.
Pokud počítáme s tím, že náš zdroj světla je bod někde v prostoru, ještě potřebujeme brát v potaz vzdálenost našeho bodu od zdroje světla. Dejme tomu, že náš zdroj světla vysvítí do prostoru kolem sebe rovnoměrně nějakou energii. Co se stane, když se budeme od zdroje vzdalovat? Pokud si představíme kouli, jejíž střed je náš zdroj světla, vždy na ni dopadne všechna jeho energie. Když se bude poloměr koule (vzdálenost od zdroje) zvětšovat, celková plocha koule poroste s druhou mocninou jejího poloměru (povrch koule je roven 4 pi r2). Tedy „hustota“ energie bude s rostoucí vzdáleností od zdroje kvadraticky klesat.
Intenzita světla v nějakém bodě, jehož vzdálenost od zdroje je r, je tedy rovna 1/r2. Opět to není přesný vztah, protože předpokládá nekonečně malý zdroj světla (takové neexistují) a nebere vůbec v potaz konstanty, ale pro naše účely bohatě stačí.
Phongův osvětlovací model
Ke spočítání osvětlení v daném bodě budeme muset nějak popsat celkovou situaci, k čemuž se používá několik vektorů:
- n, takzvaný normálový vektor či normal vector, je kolmý na povrch a ukazuje směrem ven z objektu – říká nám tedy jak je povrch orientovaný
- l, light vector, ukazuje z aktuálního bodu směrem ke zdroji světla (tedy je rovnoběžný s příchozími paprsky)
- v, view vector, ukazuje z bodu směrem k pozorovateli (oku, kameře)
- r, vektor odrazu, ukazuje z bodu směrem kam by se světlo zrcadlově odrazilo (pokud by byl povrch absolutně hladký)
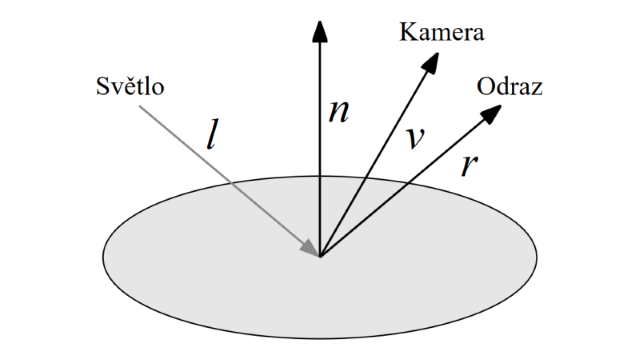
Úhel potřebný pro Lambertův zákon je vlastně úhel mezi vektory n a l.
Připomeňme, že kosinus úhlu mezi dvěma vektory lze snadno spočítat pomocí
skalárního součinu těchto dvou vektorů (v GLSL funkce dot), jen musí mít oba délku jedna, tedy
musí být normalizované (v GLSL funkce normalize).
Předpokládáme, že všechny vstupní vektory těchto rovnic normalizované jsou.
Pokud si nejste úplně jistí, co to je normalizace nebo skalární součin, odpověď najdete v našem krátkém úvodu do vektorů.
Další hodnoty popisující situaci:
- I – příchozí světlo
- Cd – odchozí difúzní světlo
- Cs – odchozí spekulární světlo
- Kd – difúzní barva povrchu
- Ks – spekulární barva povrchu
- a – „lesklost“ povrchu (vyšší hodnoty jsou lesklejší)
Nyní můžeme formulovat rovnice pro oba typy světla. Začneme s difúzním:
Je vidět, že se nejedná o nic jiného než aplikaci Lambertova zákona na příchozí světlo a absorbci části světla materiálem. Tento model není zcela přesný, nicméně pro naše účely bohatě stačí. Zatím.
V praxi je potřeba si pohlídat, že pokud je výraz n ·l záporný, tak místo něj použijeme nulu. To nastane, pokud se světlo nachází za rovinou povrchu (a tedy stejně jej nemůže nikdy osvětlit).
Spekulární světlo:
Druhý skalární součin vyjde blízko k jedné jen tehdy, pokud je pozorovatel
zhruba ve směru, kam se světlo odráží. Vyšší mocniny této hodnoty poté vedou
k ostřejšímu, méně rozptýlenému odrazu. Je třeba ošetřit, aby skalární
součiny nebyly záporné. To by nastalo, jakmile by úhel mezi vektory byl
vyšší než 90°. V takovém případě místo hodnoty skalárního součinu
použijeme nulu, čehož se v praxi docílí pomocí max(dot(...), 0.0).
Odrazový vektor r počítáme pomocí zabudované funkce GLSL reflect.
Parametr a je jakási lesklost povrchu. Stejně jako celá spekulární část Phongova modelu není nijak fyzikálně založený. Má vliv na velikost či ostrost spekulárních odrazů. Na obrázku níže jsou demonstrovány (zleva) hodnoty 4, 32 a 128.
Jak difúzní světlo Cd a spekulární světlo Cs zkombinovat? Stačí je prostě sečíst. Pokud by scéna byla osvětlená více zdroji světla, tak bychom výsledné světlo od každého také posčítali. To stejné uděláme v příštím díle, až potkáme ambientní světlo.

Normály
Nyní potřebujeme najít normálový vektor v libovolném bodě našeho povrchu. K tomu nám poslouží právě výška. Naklonění nějakého bodu můžeme zjistit z rozdílu výšky oproti jeho sousedům (posunutých o konstantu) v obou rozměrech:
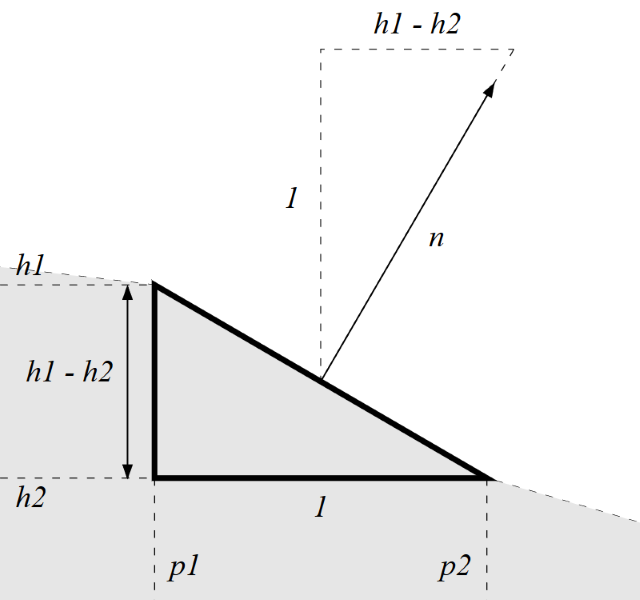
V bodě p1 jsme spočítali výšku h1, v bodě p2 (vzdáleného od p1 o jednu jednotku) výšku h2, známe tedy rozměry tlustě nakresleného trojúhelníku, jehož horní strana reprezentuje povrch v tomto místě. Čárkovaný svislý trojúhelník nad ním, jehož přepona odpovídá hledanému normálovému vektoru, je mu podobný, normálový vektor tedy umíme spočítat. Z toho už vyplývá kód pro spočítání výšky:
float getHeight(vec2 uv) {
return brick(uv).w;
}
vec3 computeNormal(vec2 uv)
{
const float diff = 0.001;
float here = getHeight(uv);
vec3 n = vec3(
here - getHeight(uv + vec2(diff, 0.0)),
here - getHeight(uv + vec2(0.0, diff)),
1.0
);
return normalize(n);
}
Normála ukazuje na našem povrchu směrem k pozorovateli, pro nás je to směrem do kladného z. Všimli jste si, že jsme se potichu přesunuli ze dvou rozměrů do tří? :-)
Zkuste si normály vizualizovat (nezapomeňte je přitom převést z rozsahu -1 až 1 do 0 až 1).
Pokud se zdají být moc „ploché“ a modré, pronásobte něčím hodnoty, které
vrací funkce getHeight.
Normálové mapy či textury se ve hrách často používají pro přidání jemných detailů do povrchů. I když je geometrie povrchu placatá, různé místa s různou normálou budou správně reagovat na světlo a vytvářet dojem výstupků a prohlubní. Níže je výřez normálové mapy, která patří k jedné z textur ze zadání prvního úkolu.

Počítáme světlo
Úkol 2 [8b]
Nasvětlete povrch (ať už cihly nebo váš vlastní) bodovým zdrojem světla, který lze ovládat pomocí kliknutí myši.
Pro získání pozice myši použijte zabudovaný vstup iMouse.xy (viz nápověda
v Shadertoy),
ve kterém jsou uloženy souřadnice posledního pixelu, na který myš
klikla. Nezapomeňte na ně aplikovat stejné korekce jako na souřadnice
současného pixelu.
Světlu nastavte nějakou konstantní výšku nad povrchem (i když potom vizuální poloha světla nebude úplně odpovídat poloze kurzoru). Stejně tak si určete nějakou konstantní výšku kamery, aby bylo z čeho spočítat view vector. Dejte pozor na to, aby různé vektory skutečně ukazovaly, kam mají, a ne opačným směrem.
Výsledek by mohl vypadat nějak takto:

Bodování (celkem 8 bodů):
- 4 body za správnou implementaci funkce osvětlovacího modelu
- 2 body za ovládání světla myší
- 2 body za správné použití výškové mapy pro normály
Už víme, jak nějakým základním způsobem simulovat světlo. Teď by se hodilo nasvětlit něco zajímavějšího, než jen plochu. Právě v příštím díle začneme pracovat s prostorovými útvary a podíváme se na zoubek raytracingu.