Čtvrtá série třicátého třetího ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Už je to tak, 33. ročník KSP pokračuje dál a čtvrtá série KSP-H je tu.

Naleznete zde 4 normální úlohy, bonusovou těžší úlohu a pak také pokračování seriálu o počítačové grafice. Všechny díly seriálu můžete odevzdávat v průběhu celého roku, takže vůbec nevadí, že jste třeba první díl nestihli. Detaily naleznete u zadání seriálu. Připomínáme, že oproti loňskému ročníku se do výsledkové listiny započítávají všechny úlohy mimo bonusové a body se již nepřepočítávají podle počtu vyřešených sérií.

Odměny & na Matfyz bez přijímaček

• Termín série: neděle 11. dubna 2021 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Každému, kdo z bonusové úlohy 33-4-X1 získá alespoň dva body, pošleme sladkou odměnu.

Zadání úloh

• 33-4-1: Ohňostroj
• 33-4-2: Firewall
• 33-4-3: Mraveniště na kopci
• 33-4-4: Prohledávání KSP webu
• 33-4-S: Raytracing
• 33-4-X1: Koření a recepty

33-4-1 Ohňostroj (12 bodů)

V řadě za sebou je N odpalovacích zařízení na ohňostroj. V každém je odpalovací mikropočítač, který je propojený s počítači sousedních odpalovacích zařízení.

Rádi bychom odpálili ohňostroj ze všech stanic současně. To ale není tak jednoduché, protože komunikace mezi sousedními stanicemi je moc pomalá. Kdyby si tedy jen předávali informaci „Odpal!“, tak by nevznikl hezký správně načasovaný ohňostroj, ale vznikla by mexická vlna. Vašim úkolem bude tento problém vyřešit.

Vymyslete program, který se nahraje do každé odpalovací stanice a nechá se běžet. Po nějakém čase obsluha zmáčkne tlačítko na libovolné ze stanic a je na vašich programech, aby poté v jeden moment odpálily všechny stanice.

Je tu ovšem jeden problém. V každé stanici máme jen omezené množství paměti na konečný počet bitů.

Pro potřeby naší úlohy si tedy můžete alokovat bitů libovolný počet, ale tento počet musí být konstantní, tedy nemůže záviset například na N. Díky tomu si ani nemůžete uložit hodnotu čísla N do každé paměti, protože ta zabere log N bitů, což již není konstanta.

Algoritmus se vyhodnocuje v ticích, které nastávají současně na všech odpalovacích stanicích. V každém tiku se na každém zařízení spustí vámi vymyšlená funkce. Ta může upravovat svoji paměť a navíc může komunikovat se sousedními mikroprocesory tím, že čte jejich paměť. Umí poznat levého a pravého souseda a také jestli je soused připojen, nebo jestli se stanice nachází na okraji řady a žádného souseda již nemá. Přesněji řečeno čte paměť sousedů ve stavu, v jakém byla na začátku tiku. Krom toho může požádat o odpálení a také číst stav tlačítka. Máte zaručeno, že tlačítko bude stisknuto pouze na jednom zařízení a to po dobu jednoho tiku.

Formálně vzato, každé zařízení se tedy chová jako konečný automat.

Za časovou složitost algoritmu považujeme počet tiků od zmáčknutí tlačítka po odpálení ohňostroje, přitom nás zajímá jen její asymptotický odhad vzhledem k N.

Část bodů dostanete i za řešení, které fungují jen pro nějaká speciální N, ovšem musí jich být nekonečně mnoho. Tedy například násobky 42, nebo třeba každé druhé prvočíslo.

Řešení

33-4-2 Firewall (10 bodů)

Tato stránka je pro Váš region nedostupná. Tato hra není povolená pro Vaší zemi. Tento kód je platný jen v některých zemích. K tomuto serveru se nemůžeš připojit, protože málo uctíváš hroší bohy …

S některými z těchto hlášek jste se mohli již setkat, např. některé filmy na Netflixu jsou uvedeny jen pro určité trhy, ať to má jakýkoliv důvod, nebo nějaké Steam klíče jsou geograficky zamčené.

Tyto geografické zákazy se dějí z větší míry pomocí IP adres, u kterých se zjišťuje, jestli je to jedna z povolených adres (whitelist), nebo jedna ze zakázaných adres (blacklist). Samozřejmě to nemusí být jediné kritérium.

V této úloze si vyzkoušíte napsat filtr na IP adresy, konkrétně na jejich starší variantu IPv4. Budete dostávat tři typy dotazů:

• A (allow) – povol danou podsíť IP adres
• B (ban) – zakaž danou podsíť IP adres
• Q (query) – dotaz: Je tato IP adresa povolená?

Podsítě budou zadány v CIDR formátu. Pokud tento formát znáte, můžete následujících pět odstavců přeskočit.

Na začátek si ujasníme pohled na IPv4 adresy. IPv4 je v podstatě 32bitové číslo. Zpravidla se zapisuje rozdělené do čtyř osmibitových čísel oddělených pro přehlednost tečkami, například 192.168.255.4 (po přepsání do dvojkové soustavy 11000000.10101000.11111111.00000100).

Počítačové sítě jsou často děleny do podsítí, ve kterých mají všechny adresy stejnou počáteční část (nazývanou prefix sítě). Často se podsítě zapisují v CIDR formátu, který vypadá jako IP adresa s číslem za lomítkem. Toto číslo, označme ho K, udává délku prefixu v bitech. Pro IPv4 je v rozmezí 0 až 32. Před lomítkem je pak IP adresa, jejíž prvních K bitů je prefix sítě a zbytek je doplněn nulami (aby měla délku 32 bitů).

Například zápis 192.168.3.0/24 označuje podsíť s 256 IP adresami ve tvaru 192.168.3.xxx (což ve dvojkové soustavě vypadá jako 11000000.10101000.00000011.xxxxxxxx).

Pro prefixy, které jsou násobky 8, je to celkem intuitivní, ale co značí třeba zápis 192.168.2.128/26? Ten označuje podsíť 64 IP adres začínající adresou 192.168.2.128 a končící adresou 192.168.2.191, neboli prvních 26 bitů adresy je pevně určeno prefixem a variabilita je jen v posledních 6 bitech. Zapsáno ve dvojkové soustavě to vypadá takto: 11000000.10101000.00000010.10xxxxxx.

Abyste si nemuseli vše ručně počítat na papír, tak doporučujeme nástroj ipcalc, existuje i jeho online verze.

Na začátku jsou všechny IP adresy zakázané. Jednotlivé operace (povolení a zakázání podsítě) se navzájem přepisují. Například pokud je povolena podsíť 192.168.0.0/16, ale později je zakázána podsíť 192.168.1.0/24, tak IP adresa 192.168.1.1 je po těchto operacích zakázána.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu dostanete číslo N udávající počet dotazů. Na dalších N řádcích budou následovat jednotlivé dotazy. Dotazy začínají písmenem A, B nebo Q. U dotazů A a B bude následovat rozsah IPv4 adres v CIDR formátu. U dotazu Q bude následovat jen samostatná IP adresa.

Formát výstupu: Pro každý dotaz typu Q vypište na samostatný řádek A, nebo N jako ANO, nebo NE, je-li IP adresa povolena, či ne.

7
Q 192.168.1.1
A 192.168.0.0/16
Q 192.168.1.1
B 192.168.1.0/24
Q 192.168.1.1
A 192.0.0.0/8
Q 192.168.1.1

N
A
N
A

Příklad: Na začátku nejsou povoleny žádné adresy a první dotaz se tak vyhodnotí na N. Potom jsme povolili podsíť 192.168.0.0/16, tudíž IP adresa 192.168.1.1 je povolena. Poté jsme zakázali podsíť 192.168.1.0/24 a IP adresa 192.168.1.1 je znovu zablokována. Nakonec je povolena podsíť 192.0.0.0/8 a IP adresa 192.168.1.1 je povolena.

Řešení

33-4-3 Mraveniště na kopci (11 bodů)

Kevinova babička má za chalupou prazvláštní kopec. Na jeho vrcholu je veliké mraveniště, kde vládne chytrá mravenčí královna. K té se jednoho dne doneslo, že na úpatí kopce se děje něco divného, a tak se rozhodla vyslat své mravenčí dělníky na průzkum.

Vyslat mravenčí dělníky na průzkum ale není tak jednoduché – když nemají vytyčenou pachovou stopu z feromonů, tak chodí docela náhodně. Přesněji když přijde mravenčí dělník na křižovatku, ze které vychází N cest, tak si hodí spravedlivou N-stěnnou kostkou (základní výbava každého mravenčího dělníka) a se stejnou pravděpodobností se vydá po jakékoliv z cest dál.

Mravenčí královna alespoň své dělníky instruovala, aby chodili vždy jen z kopce dolů (a tudíž se nemohou zamotat do žádného cyklu) – když mravenec přijde na křižovatku, tak si náhodně vybere jen z cest vedoucích dolů. Celou situaci si tak můžeme představit jako orientovaný graf, kde každý vrchol má nějakou výšku a každá hrana vede z nějakého vrcholu do vrcholu, který je ostře níž. Ještě dodejme, že když mravenec dojde do listu (vrcholu, ze kterého již nepokračuje žádná cesta dolů), tak se zde zastaví a zůstane tu.

Na vrcholu kopce je vrchol reprezentující mraveniště a někde u úpatí kopce je list, který královnu zajímá a do kterého by chtěla dostat alespoň K průzkumníků. Vaším úkolem je vymyslet algoritmus, který pro zadaný graf kopce a pro číslo K zjistí, kolik nejméně mravenců musí královna z mraveniště vyslat, aby do označeného listu došlo ve střední hodnotě alespoň K z nich.

Pokud nevíte, co znamená „ve střední hodnotě“, tak se začtěte do přiložené kuchařky.

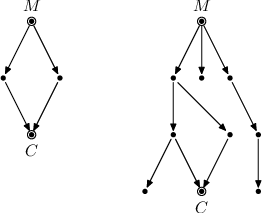
Příklad: Pro graf vlevo dojdou všichni mravenci vyslaní z mraveniště M do cíle C, takže stačí vyslat právě K mravenců. Pro pravý graf je nutné vyslat 4K mravenců, aby jich ve střední hodnotě do cíle došlo K.

Lehčí varianta (za 6 bodů): Vyřešte úlohu pro grafy, které mají podobu stromu s mraveništěm v jeho kořeni.

Řešení

33-4-4 Prohledávání KSP webu (12 bodů)

Petr si chtěl něco vyhledat na webu KSP, když tu zjistil, že jeho oblíbený globální vyhledávač nefunguje. Samotné stránky KSPčka ale fungovaly a když se ani po pár minutách situace s vyhledávačem nezlepšila, tak se rozhodl napsat si pro web KSP vyhledávač vlastní …

Toto bude v této méně tradiční open-datové úloze i váš úkol. Budete pro zadaná slova vracet URL stránek na webu KSP, na kterých se slova nachází. K tomu se bude pravděpodobně hodit znalost, jak si z vašeho programu stáhnout přes HTTP obsah zadaného URL. Níže jsme si pro vás připravili ukázky stažení jedné stránky v několika jazycích.

#!/usr/bin/python3

# Použijeme knihovnu requests, která je doporučována i oficiální dokumentací.
# Může být potřeba doinstalovat, nejsnáze asi přes pip:
#     pip3 install requests
import requests

def get_page(url):
    # Pošleme HTTP GET požadavek na zadanou adresu
    response = requests.get(url)
    # Můžeme zkontrolovat návratový kód, 200 je ok, 404 například znamená, že
    # stránka neexistuje
    if response.status_code != 200:
        print(f"Něco se pokazilo, request na URL '{url}' vrátil {response.status_code}")
        return False
    # Vrátíme tělo odpovědi
    return response.text

print(get_page("https://ksp.mff.cuni.cz/h/ulohy/27/reseni4.html"))

using System.Net;

var client = new WebClient();

// Pošle HTTP GET požadavek na zadanou adresu. Když vše projde, tak rovnou vrátí
// string, pokud stránka neexistuje nebo se pokazí něco jiného, vyhodí výjimku.
string htmlPage = client.DownloadString("https://ksp.mff.cuni.cz/h/ulohy/27/reseni4.html");

Console.WriteLine(htmlPage);

# curl je příkaz dostupný z příkazového řádku většiny Linuxů, dá se instalovat
# i na Windows

# Uložení obsahu stránky do souboru pro další zpracování
curl https://ksp.mff.cuni.cz/h/ulohy/27/reseni4.html > soubor.html

# Nebo také lze poslat stránku přímo na standardní vstup jiného programu/skriptu
curl https://ksp.mff.cuni.cz/h/ulohy/27/reseni4.html | ./program.py

Také se vám bude hodit základní znalost HTML. Ve zbytku zadání budeme předpokládat, že víte, co je to HTML tag a jak se zapisuje.

Vaším úkolem bude hledat v obsahu zadání, řešení a komentářů všech sérií (speciální nultou sérii 24. ročníku neuvažujeme) obou kategorií 0. až 32. ročníku KSP (tedy všechny mimo letošního ročníku). Na webu vás tedy budou zajímat některé části podstromů /h/ulohy/... a /z/ulohy/.... Obsahem vždy myslíme vnitřek elementu <div id='content'> na dané stránce.

Hledat budete celá slova, tedy maximální podřetězce tvořené alfanumerickými znaky (tedy písmeny a čísly, včetně písmen s diakritikou) a podtržítky. Pokud bude hledané slovo jen částí slova na stránce, tak se nejedná o shodu (například při hledání slova nasyta není slovo nenasyta shoda, protože se nejedná o shodu na celém slově). Velká a malá písmena nerozlišujte.

Technické detaily

Při práci s diakritikou si dejte pozor na to, že web KSP servíruje stránky v kódování UTF-8, takže jeden znak nemusí být vždy jeden bajt. Některé programovací jazyky před vámi problém s kódováním skryjí (například Python), v jiných ho budete muset vyřešit ručně.

HTML tagy, komentáře a entity považujeme pro jednoduchost za oddělovače slov. Například řetězec do<b>psat</b> tedy představuje dvě slova do a psat. Podobně řetězec ne…nebo ano obsahuje tři slova ne, nebo a ano.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu dostanete číslo N udávající počet vyhledávacích dotazů. Na dalších N řádcích dostanete slova (alfanumerické řetězce v UTF-8 bez mezer), která máte za úkol nalézt na KSP webu.

Formát výstupu: Pro každé slovo ze vstupu vypište na samostatný řádek cestu ke stránce na KSP webu, na které se dané slovo nachází (jen cestu bez http://ksp.mff.cuni.cz). Při nalezení slova na více stránkách vypište jednu libovolnou z nich. Slibujeme, že každé slovo na vstupu lze na webu nalézt na alespoň jedné stránce.

3
anekdota
cestář
berňák

/h/ulohy/24/zadani3.html
/h/ulohy/20/zadani3.html
/h/ulohy/25/zadani4.html

Pokud byste narazili na nějaké technické problémy při implementaci, ozvěte se nám na našem Discordu, zkusíme vám poradit.

Řešení

33-4-X1 Koření a recepty (10 bodů)

Chtěli byste si otevřít restauraci a přemýšlíte o tom, jaká jídla připravovat. Znáte recepty R₁, … R_n, na jejichž přípravu potřebujete některá z koření K₁, … , K_m. Nákup koření K_i stojí cenu k_i, po pořízení ho máte k dispozici libovolné množství. Recept R_j můžete připravit a utržíte za něj částku r_j, pokud máte všechna potřebná koření.

Vymyslete algoritmus, jenž pro zadané ceny koření, výdělky receptů a bipartitní graf závislostí receptů na koření stanoví, která koření pořídit, abychom na přípravě receptů vydělali co nejvíce. Chceme tedy maximalizovat rozdíl tržeb (součet výdělků receptů, které umíte uvařit) a nákladů (součet ceny koření, která jste koupili).

Řešení

33-4-S Raytracing (15 bodů)

Toto je seriálová úloha, která navazuje na podobné úlohy v minulých sériích. Pokud jste předchozí díly seriálu neřešili, pro pochopení tohoto dílu je dobré si je nejméně přečíst. A pokud si chcete úlohy z minulých dílů také naprogramovat, stále za ně můžete získat polovinu bodů.

Nastal čas vydat se v našich grafických toulkách do hlubokého světa třetí dimenze. Dnešním tématem je raytracing a vykreslování prostorových scén.

Raytracing je způsob vykreslování, ve kterém se sledují trasy nějakých paprsků. Typicky se pro každý pixel obrázku vystřelí do scény jeden parsek (jak, to záleží na kameře, kterou simulujeme), sleduje se jeho dráha a zjistí se, kde dojde ke kolizi se scénou. Poté se v tomto místě spočítá osvětlení, které po tomto paprsku doputovalo k pozorovateli, a podle něj se zabarví pixel obrázku.

Z místa kolize můžeme vystřelit druhý paprsek směrem ke světlu a sledovat, jestli do něj dorazí nebo ne. Pokud nedorazí, mezi bodem kolize a zdrojem světla se nachází nějaká překážka a kolize tedy bude ve stínu. Stejně tak můžeme z bodu kolize vystřelit paprsek směrem, kam by se původní odrazil, a tím spočítat zrcadlové odrazy. Pokud chceme vícenásobné zrcadlové odrazy, můžeme tento postup rekurzivně opakovat.

Napíšeme si vlastní jednoduchý raytracer. Jeho nejdůležitější částí je počítání kolizí paprsků se scénou. Pro klasické scény ze složitých polygonových objektů je to velmi výpočetně náročné, a proto se raytracing ve hrách začíná ve velkém využívat až nyní s příchodem specializovaného hardwaru. My ale tento problém můžeme obejít tím, že použijeme nějakou jednodušší reprezentaci scény.

Protože budeme v tomto dílu hodně pracovat s vektory, připomínáme náš úvod do vektorů.

V tomto díle na sebe hodně úkolů postupně navazuje, takže jestli chcete, můžete odevzdat více úkolů dohromady jako jeden soubor s kódem shaderu. Všechny zdrojáky (jako vždy) zabalte do zip souboru.

Signed distance function

Signed distance function, česky „znaménková vzdálenostní funkce“, zkráceně SDF, je způsob reprezentace scény pomocí funkce, která pro každý bod v prostoru vrátí vzdálenost k nejbližšímu povrchu. Navíc, pokud se bod nachází uvnitř nějakého objektu, tak je tato vzdálenost záporná a její absolutní velikost udává vzdálenost k nejbližšímu bodu mimo objekt.

Jak si takovou funkci pořídit? Například pro kouli nebo kruh je to snadné: spočítáme vzdálenost bodu od středu a odečteme od této hodnoty poloměr. Rozmyslete si, že toto nám opravdu vrátí správnou znaménkovou vzdálenost. Tato funkce by se dala vizualizovat následovně:

Žluté barvy jsou kladné hodnoty vzdálenosti, modré jsou záporné.

Silnou stránkou SDF je, že na nich můžeme snadno provádět množinové operace. Sjednocení dvou SDF uděláme tak, že použijeme menší z jejich hodnot, tedy minimum:

Vnější vzdálenosti jsou v této kombinaci správně, všimněte si ale, že uvnitř jsou sjednocené vzdálenosti špatně. Kolem ostrých rohů, kde kruh splývá se čtvercem, by měly vnitřní vzdálenosti tvořit kruhové vrstvy. Tento problém nemá žádné jednoduché řešení, ale naštěstí jej můžeme ignorovat. Bude nám stačit mít správné vnější vzdálenosti. A dokonce nemusíme mít ani to. Později narazíme na SDF, které vrací jen dolní odhad vzdálenosti a i to bude pro naše účely dostačující.

Průnik dvou SDF provedeme tím, že z obou hodnot vezmeme maximum:

Tento způsob reprezentace scény je u shaderových raytracerů velmi rozšířený – pokud v Shadertoy najdete shader s nějakou prostorovou scénou, velmi pravděpodobně používá právě SDF. Mnoho užitečných SDF primitiv a technik naleznete na tomto odkazu.

Raymarching

Máme reprezentaci scény a nyní potřebujeme spočítat kolizi s paprskem. To se u SDF dělá takzvaným raymarchingem, tedy kráčením po paprsku.

Začneme v počátku paprsku. Pro aktuální pozici zjistíme d – hodnotu vzdálenostní funkce. Jelikož d je vzdálenost k nejbližšímu povrchu (nebo dolní odhad této vzdálenosti), máme zaručeno, že v kouli o poloměru d okolo aktuálního bodu není žádná kolize. Můžeme se tedy pohnout o d po směru paprsku a máme zaručeno, že žádnou potenciální kolizi nepřeskočíme.

Tento postup opakujeme, dokud d neklesne pod nějaké dostatečně malé epsilon, potom prohlásíme, že jsme nalezli kolizi. Pokud naopak uražená vzdálenost překročí nějakou horní hranici, řekneme, že paprsek vyletěl ze scény do nekonečna.

Této variantě raymarchingu, kde v každém bodě známe poloměr koule, ve které se zaručeně nenachází kolize, se někdy říká sphere tracing. Raymarching jako takový je obecnější algoritmus, který lze použít například při vykreslování mlhy, kdy skáčeme po krocích pevné velikosti a pro každou navštívenou pozici přečteme hustotu mlhy z nějaké šumové funkce nebo trojrozměrného pole.

Střílíme paprsky

Ještě potřebujeme dvě věci. První z nich je způsob, jak spočítat ze SDF normálu povrchu v nějakém bodě. To provedeme funkcí computeNormal (viz kód u prvního úkolu), která je odvozená podobným způsobem jako počítání normály z výškové mapy v minulém díle.

Druhou věcí je vygenerování paprsků samotných pro každý pixel obrazovky. Naše kamera bude definovaná svou pozicí, a směrem, kam se dívá. Všechny paprsky budou mít počátek v bodě, kde se nachází kamera. Někde ve směru, kam se kamera dívá, si představíme obdélník obrazovky. Pro každý pixel vygenerujeme paprsek tak, že protne střed daného pixelu na této pomyslné obrazovky. Také si to můžeme představit tak, že kamera se nachází uprostřed vašeho oka a paprsky z něj míří doprostřed každého pixelu monitoru, na který se (pravděpodobně) díváte.

Obdélník obrazovky bude orientovaný tak, že jeho plocha bude vždy kolmá na osu z jeho středu ke kameře (tedy směr, kam se kamera dívá). Jen pozice a směr pro pořádnou definici kamery nestačí, ještě musíme popsat, jak bude obdélník natočený podle osy směru, kam se kamera dívá. My jej vždy natočíme tak, že jeho horní a dolní hrany budou vodorovné.

Tento styl kamery se běžně používá ve hrách. Její střed je definovaný pozicí hráče a směr kamery ovládáme myší.

Na generování paprsků pro přesně tuto kameru dostanete funkci getRayDirection, jejíž kód naleznete u zadání prvního úkolu. Tato funkce umí pro každý pixel obrazu vygenerovat vektor směru paprsku, a to pomocí souřadnic pixelu uv (v rozsahu -1 až 1), vektoru forward (směru, kam se kamera dívá) a horizontálního zorného úhlu (ve hrách se mu říká field of view či fov). Vzdálenost mezi kamerou a pomyslným obdélníkem obrazovky vypočítáme tak, aby úhel mezi kamerou a jeho levým a pravým okrajem byl právě zadaný horizontální zorný úhel hfov. Velikost obdélníku obrazovky si funkce sama zjistí ze zabudovaných vstupů v Shadertoy.

Úkol 1 [2b]

Naprogramujte raymarchovací funkci raymarch do níže uvedené kostry shaderu.

Jelikož to je něco, na čem se dá poměrně snadno spálit, připomínáme adresu zdrojaky@ksp.mff.cuni.cz, kde vám s radostí poradíme. Pokud jste na něčem zaseklí déle než půl hodiny, určitě pište!

Raymarchovací funkce dostane souřadnice počátku paprsku (origin) a normalizovaný vektor směru paprsku (direction) a má vrátit vzdálenost, kterou musí paprsek urazit, než narazí na nejbližší kolizi. Pokud paprsek urazí vzdálenost větší než konstanta FAR a na žádnou kolizi nenarazil, tak předpokládáme, že vystřelil do nekonečna a vrátíme libovolnou hodnotu větší než FAR (abychom mohli později snadno zjistit, jestli paprsek do něčeho narazil nebo ne pomocí porovnání raymarch(...) < FAR).

Ve funkci použijete nějakou smyčku. Je dobrý nápad omezit její maximální počet iterací (třeba na 128). Pokud smyčka skončí kvůli velkému počtu iterací, budeme se tvářit, že paprsek vyletěl do nekonečna a prostě vrátíme vzdálenost FAR.

V kódu se nachází jednoduchá SDF scéna tvořená sjednocením tří koulí a roviny - p.y je vzdálenostní funkce vodorovné roviny ve výšce 0. Scénu klidně rozšiřte o další objekty, jestli chcete (ale není to součást úkolu).

Pokud se vám editor seká, můžete vypnout pravidelné překreslování obrazu pomocí tlačítka „pause“. Když se změní pozice myši nebo překompiluje shader, obraz se stále obnoví.

#define PI 3.1415926535897932384626433832795

// Tuto vzdálenost budeme považovat za nekonečno
#define FAR 50.0

float sdfSphere(vec3 center, float radius, vec3 p)
{
    return length(center - p) - radius;
}

float sceneSdf(vec3 p)
{
    // Podlaha je prostor mezi dvěma rovinami
    float d = max(p.y, -p.y - 0.5);
    d = min(d, sdfSphere(vec3(0.0, 1.0, 0.0), 1.0, p));
    d = min(d, sdfSphere(vec3(-3.0, 0.8, 0.0), 0.8, p));
    d = min(d, sdfSphere(vec3(3.0, 1.2, 0.0), 1.2, p));
    return d;
}

// Raymarchovací funkce
// Vstupy:
// origin - počátek paprsku
// direction - směr paprsku (vektor normalizovaný na velikost 1)
// Výstup: vzdálenost, kterou musí paprsek urazit, než narazí na kolizi
// nebo hodnota větší nebo rovna než FAR, pokud do vzdálenosti FAR na
// žádnou kolizi nenarazil.
// Nezapomeňte smyčku ukončit, pokud hodnota SDF klesne pod nějaké epsilon
// nebo pokud se provede příliš mnoho iterací.
float raymarch(vec3 origin, vec3 direction)
{
    // TODO: sem doprogramujte raymarching
}

vec3 computeNormal(vec3 p)
{
    const float epsilon = 0.001;
    float here = sceneSdf(p);
    return normalize(vec3(
        sceneSdf(p + epsilon * vec3(1.0, 0.0, 0.0)) - here,
        sceneSdf(p + epsilon * vec3(0.0, 1.0, 0.0)) - here,
        sceneSdf(p + epsilon * vec3(0.0, 0.0, 1.0)) - here
    ));
}

// forward: normalizovaný vektor dopředu
// uv: souřadnice pixelu v -1..1
// hfov: horizontální zorný úhel ve stupních
vec3 getRayDirection(vec3 forward, vec2 uv, float hfov)
{
    // Z "forward" vygenerujeme i vektory vpravo a nahoru, vše normalizované
    // a navzájem kolmé
    vec3 right = normalize(cross(forward, vec3(0.0, 1.0, 0.0)));
    vec3 up = normalize(cross(right, forward));
    // Převedeme hfov na radiány
    hfov = hfov / 180.0 * PI;
    // Spočítáme vzdálenost roviny od kamery
    float dist = 1.0 / tan(hfov * 0.5);
    // Přeškálujeme "up" tak, aby byl zachován poměr stran
    up *= iResolution.y / iResolution.x;
    vec3 ray = forward * dist + right * uv.x + up * uv.y;
    return normalize(ray);
}

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    vec2 uv = fragCoord / iResolution.xy;
    // Střed souřadnic chceme uprostřed obrazu
    uv = uv * 2.0 - 1.0;

    vec3 cameraPosition = vec3(0.0, 2.0, 6.0);
    vec3 cameraLookAt = vec3(0.0, 1.0, 0.0);

    vec3 rayDirection = getRayDirection(
        normalize(cameraLookAt - cameraPosition),
        uv, 80.0);

    float depth = raymarch(cameraPosition, rayDirection);

    // Souřadnice dopadu paprsku
    vec3 hit = cameraPosition + rayDirection * depth;
    // Normála povrchu v bodě dopadu
    vec3 normal = computeNormal(hit);

    // Převedeme normálu na barvu
    vec3 color = normal * 0.5 + 0.5;

    // Dolní pravý trojúhelník obrazu
    // vyplníme vizualizací hloubky
    if(uv.x > uv.y)
    {
        color = vec3(1.0 / depth * 2.0);
    }

    if(depth > FAR)
    {
        color = vec3(0.0);
    }

    // Output to screen
    fragColor = vec4(color, 1.0);
}

Tento shader bude zobrazovat zároveň normálu v místě dopadu paprsku (levý horní trojúhelník) a zároveň hloubku (pravý dolní). Pokud je vaše raymarchovací funkce správně, výsledek by měl vypadat takto:

Úkol 2 [3b]

Naprogramujte ovladatelnou kameru pomocí myši, viz zabudovaný vstup iMouse.xy - pozor, že je v pixelech a že složka y roste směrem nahoru.

Hezký styl ovládání je, že se kamera pohybuje na povrchu koule, v jejímž středu je bod cameraLookAt a kamera míří vždy na něj.

Bude se vám hodit tato funkce, která pro zadaný horizontální a vertikální úhel vrátí souřadnice daného místa na jednotkové kouli. (Úhly si můžete představit jako GPS souřadnice.)

// Pro místo na jednotkové kouli zadané
// pomocí úhlů vrátí jeho 3d souřadnice
// Vstup jsou úhly v radiánech
// První úhel je horizontální, druhý vertikální
vec3 anglesToPosition(float hor, float ver)
{
    return vec3(
        cos(ver) * sin(hor),
        sin(ver),
        cos(ver) * cos(hor)
    );
}

Gamma korekce

Ještě než do raytraceru přidáme počítání světla z minulého dílu, je třeba se zamyslet nad tím, co počítáme a co zobrazujeme.

Doteď jsme v shaderu počítali jen s barvou, kterou jsme přímo zobrazovali na monitor. Nějak automaticky jsme předpokládali, že vztah mezi zobrazovanou a vnímanou světlostí je lineární: pokud je jedna hodnota barvy dejme tomu dvakrát větší než jiná, tak ji také budeme vnímat jako dvakrát světlejší. Toto při zobrazování barev na monitor zhruba platí.

Lidské vnímání světla ale lineární není: je citlivější na nízké hodnoty. Nicméně vztah mezi zobrazovanou světlostí na monitoru a vnímanou světlostí je lineární. Důvodem je, že samotné zobrazování barev na monitor též lineární není. Reálné množství světla, které opouští pixel rozsvícený na barvu i, je přímo úměrné asi i^2.2. Tato konstanta vyplývá z vlastností starých CRT obrazovek.

Naštěstí pro lidské vidění platí, že pokud do oka dopadá světlo i, vnímáme přibližně světlost i^(1.0/2.2). Transformace v monitoru se tedy vyruší s transformací v našich očích a barvy jsou tedy lineární.

Pro nás to ale znamená, že pokud chceme zobrazovat konkrétní intenzitu světla a ne „vnímanou“ barvu, musíme onu „automatickou“ korekci z monitoru sami kompenzovat. Proto před zobrazením barvy na monitor provedeme následující umocnění:

fragColor.rgb = pow(color, vec3(1.0/2.2));

Protože odteď v seriálu budeme počítat jen intenzity světla, tuto korekci vždy používejte.

Odbočka: toto ale není jediné místo, kde se dá na nelinearitě vnímání světlostí spálit. Ve hrách se jako zdroj difúzní barvy typicky používají textury, ve kterých je třeba fotka nějakého povrchu. A hodnoty v takové textuře budou nejspíš lineární vzhledem k vnímané světlosti. Pokud je chceme interpretovat jako množství světla, které nějaký povrch odrazí, musíme je převést tak, aby byly lineární vzhledem k intenzitě světla a nikoliv vnímané světlosti. Kód by pak vypadal nějak takto:

float gamma = 2.2;

vec3 diffuseColor = texture(diffuseMap, uv).rgb;

// Nyní je diffuseColor lineární vzhledem
// k vnímané světlosti.

diffuseColor = pow(diffuseColor, vec3(gamma));

// Nyní je diffuseColor lineární vzhledem
// k intenzitě světla a můžeme s ním spočítat
// osvětlení (třeba do proměnné light)

// Nakonec opět převedeme na vnímané světlosti
fragColor.rgb = pow(light, vec3(1.0 / gamma));

Gamma korekce textur není potřeba v rámci seriálu řešit (na rozdíl od gamma korekce u výstupu).

Úkol 3 [3b]

Implementujte do raytraceru Phongův osvětlovací model z minulého dílu seriálu. Implementujte osvětlení od slunce, ambientní světlo a oblohu (viz níže).

Scénu osvětlete pomocí falešného „slunce“. Slunce se implementuje tak, že light vector i intenzita příchozího světla je stejná pro všechny body scény (předpokládáme totiž, že všechny příchozí paprsky jsou rovnoběžné, tudíž že slunce je nekonečně malý bod nekonečně daleko).

Pokud jste minulý díl neřešili, použijte tento jednoduchý model:

// diffuseColor - barva povrchu
// normal - (normalizovaná) normála povrchu
// lightColor - barva světla
// lightDirection - (normalizovaný) směr ke zdroji světla
vec3 computeLight(vec3 diffuseColor, vec3 normal, vec3 lightColor, vec3 lightDirection)
{
    return diffuseColor * max(0.0, dot(normal, lightDirection)) * lightColor;
}

Aby nebyly stíny absolutně temné, použijeme velmi jednoduchou aproximaci globální iluminace: prostě na celou scénu aplikujeme nějaké konstantní „ambientní“ světlo. V praxi k finální hodnotě přičtete toto světlo pronásobené aktuální difúzní barvou povrchu.

Materiál použijte buď konstantní pro celou scénu, nebo jej zkuste udělat různý na základě místa kolize paprsku se scénou. Například takto lze zabarvit rovinu podlahy jinak než objekty na ní ležící.

Pixely, kde paprsek odletěl do nekonečna, zabarvěte nějakým barevným přechodem, který tvoří dojem oblohy (nemusí být nijak složitý, přechod mezi dvěma barvami bohatě stačí).

Úkol 4 [2b]

Implementujte stíny od slunce.

Bod je osvětlen sluncem právě tehdy, když mezi ním a sluncem neleží žádná překážka. Jak to zjistíme? Vystřelíme směrem ke slunci paprsek! Pokud do něčeho narazí, mezi bodem a sluncem je překážka, a osvětlení od slunce nezapočítáme (ale ambientní světlo ano).

Dejte pozor na to, že pokud byste vystřeliti paprsek z místa kolize, funkce raymarch by vám ihned vrátila nulu, protože v místě kolize je vzdálenostní funkce nutně menší než epsilon uvnitř raymarch (protože její předchozí volání se v tomto místě zastavilo). Toto lze obejít tím, že výchozí bod nového paprsku posuneme trochu směrem „ven“ z povrchu pomocí normály v tomto bodě, stačí třeba o 0.02.

Úkol 5 [3b]

Implementujte do raytraceru zrcadlové odrazy.

Zde by se hodila rekurze, ovšem shadery rekurzi neumí, tudíž je nutné obejít se bez ní. Také se vám bude hodit zabudovaná funkce GLSL reflect.

Opět je třeba vystřelit z místa kolize paprsek, tentokrát tam, kam by se původní paprsek odrazil. Též je potřeba jeho výchozí bod trochu posunout, tentokrát je vhodné použít posunutí ve směru nového paprsku.

Na místě kolize nového paprsku spočítejte osvětlení (klidně i včetně stínů, ale bez dalších vnořených odrazů) a výsledek přičtěte k osvětlení ze současné kolize, ale vynásobený nějakou konstantou.

Aby scéna vypadala zajímavě, udělejte zrcadlo pouze z jedné koule. Zda paprsek dopadl právě na ten správný objekt lze zjistit třeba tak, že pro daný objekt spočítáte SDF v místě dopadu, a pokud vyjde menší než nějaké epsilon (třeba 0.03), tak se místo dopadu nachází na daném objektu. Stejným postupem můžete různé objekty různě zabarvit.

Pokud nastavíte směr ke slunci na normalize(vec3(0.9, 0.8, 1.0)), difúzní barvu koulí na vec3(0.5), barvu země na vec3(0.3, 0.5, 0.3) a spekulární barvu všeho na vec3(0.5) a spekulární „lesklost“ a na 8.0, výsledek předchozích tří úkolů by měl vypadat nějak takto:

Fraktály podruhé

Nyní máme hotový jednoduchý renderer SDF scény. Pojďme s ním něco zajímavého udělat!

V prvním díle jsme si hráli s Mandelbrot a Julia fraktály, což byly takové množiny komplexních čísel, kde pro funkci

je posloupnost f_c(0), f_c(f_c(0)), f_c(f_c(f_c(0))), … omezená. Tyto fraktály můžeme kromě komplexních čísel definovat i pro kvaterniony, což je rozšíření komplexních čísel na čtveřici hodnot. Kromě reálné a imaginární složky i je v kvaternionech také j a k.

Důležité je, že i pro kvaterniony tvoří tyto množiny zajímavé obrazce. Tyto obrazce jsou sice čtyřrozměrné, ale můžeme si je promítnout do prostoru tím, že jednu komponentu čtyřrozměrné pozice nastavíme na nulu. Získáme tím jakousi 3D obdobu těchto fraktálů.

K tomu, abychom se na tyto fraktály podívali naším raytracerem, potřebujeme někde získat jejich vzdálenostní funkci. Něco takového naštěstí existuje, nicméně není to pravá vzdálenostní funkce, vrací totiž jen dolní odhad vzdálenosti. To nám ale pro vykreslování stačí. Níže je kód této vzdálenostní funkce, založený na tomto článku.

vec4 quaternionMultiply(vec4 q, vec4 r)
{
    vec4 t;
    t.x = r.x*q.x - r.y*q.y - r.z*q.z - r.w*q.w;
    t.y = r.x*q.y + r.y*q.x - r.z*q.w + r.w*q.z;
    t.z = r.x*q.z + r.y*q.w + r.z*q.x - r.w*q.y;
    t.w = r.x*q.w - r.y*q.z + r.z*q.y + r.w*q.x;
    return t;
}

float lengthSquared(vec4 v)
{
    // dot(v, v) = v.x*v.x + v.y*v.y
    // + v.z*v.z + v.w*v.w = length(v)^2
    return dot(v, v);
}

float sdfMandelbrot(vec4 z, vec4 c)
{
    vec4 dz = vec4(1.0, 0.0, 0.0, 0.0);

    const int iterations = 32;

    for (int i = 0; i < iterations; i++)
    {
        dz = 2.0 * quaternionMultiply(z, dz);
        z = quaternionMultiply(z, z) + c;
        if (lengthSquared(z) > 256.0)
            break;
    }

    float distance = sqrt(
            lengthSquared(z) / lengthSquared(dz)
        ) * 0.5 * log(lengthSquared(z));

    return distance * 0.5;
}

Úkol 6 [2b]

Vykreslete prostorový Julia fraktál. Aby byl dobře vidět fraktálovitý interiér, usekněte horní půlku fraktálu rovinou.

Fraktál rozsekněte pomocí sjednocení nebo průniku s vhodným objektem způsobem popsaným na začátku tohoto dílu.

Parametr z fraktálu nastavíme podle pozice v prostoru. Dobře funguje, když 3D prostor namapujete na 4D kvaterniony prostě tak, že první tři komponenty zkopírujete a poslední komponentu necháte nulovou. Také je třeba nastavit parametr c na něco zajímavého (pro nulu je fraktál jen koule), dobře funguje třeba vec4(-1.5,7,16.5,-6)/22.0, ale pokuste se najít vlastní zajímavý bod.

Aby se fraktál vykresloval spolehlivě, je potřeba mírně modifikovat raymarchovací funkci. Konkrétně je třeba zajistit, že se nikdy neprovede krok delší než 2. Jinak by fraktál mohl být přeskočen (jeho vzdálenostní funkce nefunguje dobře, když jste od fraktálu daleko).

Také epsilon v raymarchovací funkci má velký vliv na vzhled fraktálu. Nižší hodnoty vedou k detailnějšímu povrchu za cenu zhoršeného výkonu. Výkon můžete ladit též pomocí počtu iterací ve funkci fraktálu.

Pro parametry cameraPosition = vec3(0.0, 2.0, 2.0) a cameraLookAt = vec3(0.0, 0.5, 0.0) a fraktál se středem ve výšce 1 by měl výsledek vypadat takto:

Kuba Pelc

Řešení