Třetí série třicátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 36-3-1: Modla pro hroší bohy
- 36-3-2: Paměťově omezený tablet
- 36-3-3: Hromady odpadu
- 36-3-4: Nejlepší programovací jazyk, část III.
- 36-3-X1: Výlet do Japonska
 36-3-1 Modla pro hroší bohy (Zadání)
36-3-1 Modla pro hroší bohy (Zadání)
Stranu, na které je kámen nejvyšší, najdeme tak, že projdeme všechny strany a spočítáme odpovídající výšky. Nejprve si můžeme uvědomit, že nejvyšší bod vždy bude jeden z vrcholů. Žádný vnitřní bod to očividně nebude a body na stranách vždy leží mezi koncovými vrcholy. Můžeme tedy projít všechny vrcholy a spočítat jejich výšky, tedy vzdálenosti od přímky, na které leží daná strana.
Vzdálenost vrcholu v→ od přímky dané vrcholy a→ a b→ se dá spočítat tak, že od vrcholu v→ odečteme jeden z vrcholů na přímce, vezmeme skalární součin s normálovým vektorem m→ = (ay - by, bx - ax), vydělíme jeho velikostí a nakonec vezmeme absolutní hodnotu:
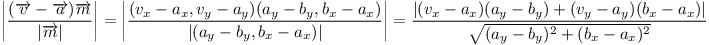
Snadno se dá ukázat, že takto opravdu dostaneme požadovanou vzdálenost. Relativní pozice vrcholu v→ vůči vrcholu a→ se dá rozložit na složky rovnoběžně s přímkou (násobek b→ - a→) a kolmo na přímku (násobek m→):
Když toto dosadíme do skalárního součinu s normálovým vektorem dostaneme:
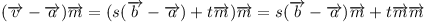
| 2 |
| x |
| 2 |
| y |
Tento algoritmus je sice správný, ale pro každou stranu prochází všechny vrcholy, takže má kvadratickou časovou složitost. Využijeme tedy toho, že je mnohoúhelník konvexní. Uvažme pro každý vrchol směr k tomu následujícímu a označme si to jako směr strany ležící mezi nimi. Pokud jsou vrcholy v pořadí proti směru hodinových ručiček, strana, na které mnohoúhelník leží, má směr přímo doprava. Když projdeme celý obvod, směr se v každém kroku otočí o trochu proti směru hodinových ručiček a dohromady udělá jednu celou otočku.
Nejvyšší vrchol bude právě na rozmezí stran se směrem nahoru a těch se směrem dolů. Pokud tedy začneme s hledáním na spodní straně, můžeme skončit, když narazíme na první vrchol, který je níž než ten předchozí. Když „převalíme“ kámen na následující stranu, odpovídá to tomu, že se mnohoúhelník a směry všech stran otočí o trochu po směru hodinových ručiček. Tím se také posune rozmezí stoupajících a klesajících hran. Když tedy hledáme nový nejvyšší vrchol, můžeme začít na tom předchozím, který teď leží někde vpravo mezi rozmezím a spodní stranou.
Toto nám dává rychlejší algoritmus. Na začátku v lineárním čase najdeme nejvyšší vrchol pro první stranu. V každém dalším kroku ho pak jenom posouváme, dokud nenarazíme na rozmezí. Jelikož nejvyšší vrchol se vždy posouvá jenom jedním směrem a nikdy nepředběhne spodní stranu, obejde celý mnohoúhelník maximálně jednou a dohromady to zabere jenom O(N). Celkově je tedy časová i paměťová složitost O(N).

| a |
| b |
| c |
| d |
 36-3-2 Paměťově omezený tablet (Zadání)
36-3-2 Paměťově omezený tablet (Zadání)
V úloze hledáme takové pořadí vyhodnocování binárního stromu „obrázkového“ výpočtu, které si v jeden okamžik potřebuje pamatovat co nejméně obrázkových mezivýsledků. K nalezení optimální strategie nám pomohou dvě pozorování.
Pozorování první: v libovolném okamžiku při vyhodnocování libovolného podstromu si musíme pamatovat vždy aspoň jeden mezivýsledek. Za mezivýsledek v tomto kontextu považujeme i výsledek celého podstromu.
Proč? Ve stromě máme dva typy vrcholů: listy a vnitřní vrcholy. Podívejme se, co se děje při jejich vyhodnocování. Pro vyhodnocení listu je třeba načíst a zapamatovat si jeho obrázkovou hodnotu, tedy jeden mezivýsledek. Neuvažujeme zde samotný počátek vyhodnocování, kdy není ani nic načteno v listech, není pro nás zajímavý. Pro vyhodnocení vnitřního vrcholu je třeba si v prvním kroku zapamatovat jeden až dva mezivýsledky jeho (jednoho až dvou) potomků a k tomu navíc paměť na výsledek vrcholu samotného, dohromady tedy dva až tři obrázky, a po spočtení výsledku operace toho vrcholu použijeme paměť na jeden výsledný obrázek. (Mimochodem, právě jsme nenápadně použili důkaz indukcí, od listů stromu až ke kořeni.)
Pozorování druhé: Všimněme si, že když chceme vyhodnotit nějaký vrchol, optimální strategie je nejdříve vyhodnotit kompletní podstrom pod jedním jeho potomkem, a poté kompletně vyhodnotit podstrom pod druhým. Tedy nikdy nedává smysl strategie, která vyhodnotí jeden z podstromů částečně, pak „přepne“ výpočet do druhého podstromu, pak se vrátí do prvního, a tak podobně.
Proč? Pokud kompletně vyhodnotíme jeden podstrom pod nějakým vrcholem, při vyhodnocování druhého podstromu si po celou dobu budeme muset pamatovat navíc jeden mezivýsledek, a to výsledek prvního podstromu. Mohli bychom se pokusit vyhodnotit první podstrom jen částečně, z prvního pozorování ale vyplývá, že v žádném bodě výpočtu prvního podstromu situace nemůže být lepší, vždy si aspoň jeden mezivýsledek k prvnímu podstromu stejně budeme muset pamatovat.
Důsledkem tohoto druhého pozorování je, že hledání optimálního pořadí výpočtu stromu je vlastně ekvivalentní průchodu stromem do hloubky, od kořene k listům, kde se v každém vrcholu ptáme, jestli je výhodnější nejdříve vyhodnotit levý podstrom a pak pravý, nebo naopak.
Mějme „magickou krabičku“, která pro daný podstrom výpočtu umí vrátit jeho „náročnost“, tedy kolik nejvýše paměti na mezivýsledky použije optimální pořadí vykonávání tohoto podstromu. Zkusíme pomocí krabičky rozhodnout, jak vyhodnotit optimálně nějaký vrchol, tedy kterého jeho potomka (podstrom pod potomkem) je výhodnější vykonat první.
Označme M (M jako menší) náročnost toho méně náročného potomka a V (V jako větší) náročnost toho náročnějšího potomka. Nyní můžeme zanalyzovat celkovou náročnost výpočtu pro obě varianty, označené CM pokud nejdříve vykonáme méně náročný podstrom, a CV pokud nejdříve vykonáme náročnější podstrom. Náročnost druhého vykonávaného podstromu se vždy větší o mezivýsledek prvního vykonávaného podstromu.
Všimněme si, že pokud M a V jsou stejné, na pořadí výpočtu nezáleží. Pokud jsou ale M a V různé, tedy M je aspoň o jedna menší než V, poté víme, že max(M, V + 1) = V + 1 a max(V, M + 1) = V. Výrazy můžeme tedy upravit následovně:
Nyní je vidět, že je vždy výhodnější vykonat nejdříve potomka s náročnějším podstromem, protože celková náročnost vrcholu poté bude menší.
Teď už máme vše potřebné pro konstrukci algoritmu, který optimální pořadí výpočtu najde. Vyrobíme rekurzivní funkci, která pro daný vrchol rozhodne, kterého jeho potomka je třeba vyhodnotit nejdříve, a zároveň vrátí paměťovou náročnost výpočtu podstromu pod daným vrcholem. Tato funkce nejdříve spustí sebe sama na obou potomcích vrcholu (zanedbejme případ, kdy má vrchol jen jednoho potomka), čímž zjistí jejich paměťové náročnosti, a jako prvního vykonaného označí toho náročnějšího z potomků.
V rekurzivní funkci musíme také dbát na to, že pokud má vrchol, na kterém se spustila, dva syny, jeho paměťová náročnost bude vždy nejméně 3, protože musíme mít v paměti aspoň prostor na výsledek daného vrcholu a mezivýsledek obou jeho synů. Stejně tak pokud má vrchol jen jednoho syna, jeho paměťová náročnost je vždy nejméně 2.
Samotné pořadí vykonávání jednotlivých vrcholů můžeme nyní získat druhým rekurzivním průchodem stromu, který „odsimuluje“ výpočet, tedy nejdříve se zarekurzí do potomka, který by měl být vykonán první. Tato druhá rekurzivní funkce vypíše na výstup daný vrchol v okamžiku, kdy ho opustí.
Toto řešení má časovou složitost lineární s počtem vrcholů stromu.
 36-3-3 Hromady odpadu (Zadání)
36-3-3 Hromady odpadu (Zadání)
Nejprve si všimneme, že kdykoliv v libovolné optimální posloupnosti operací snižujeme nějakou hromadu odpadu a někdy později ji rozdělíme na dvě části, tak nám určitě neuškodí, pokud tyto dvě operace prohodíme. Každou optimální posloupnost operací tedy můžeme přeskládat tak, že nejprve hromady pouze rozdělujeme a nakonec je všechny rozleptáme kyselinou.
Pomalé řešení
Z předchozího pozorování víme, že stačí nalézt libovolné optimální řešení, které nejprve hromady nějak vhodně rozdělí a následně je teprve snižuje. Počet snižování, který bude nutné provést, je pak roven výšce nejvyšší hromady po dělení. Chceme tedy nalézt takovou maximální výšku po dělení, při které je součet minimálního počtu dělení nutného k jejímu dosažení a následný počet použití kyseliny nejnižší možný.
Pojďme si úlohu zjednodušit a zkusme nejprve zjistit, jaký minimální počet operací je nezbytný k úklidu hromad při maximální výšce po dělení právě v.
Protože je při výšce v počet použití kyseliny předem známý, potřebujeme pro každou hromadu jen zjistit, jakým způsobem ji máme na minimální počet operací rozdělit, aby žádná její část nebyla větší než přípustná výška. Nahlédneme, že kdykoliv potřebujeme snížit nějakou hromadu, tak se nám vyplatí z ní oddělit co největší kus, ideálně díl velikosti v. Z toho plyne, že náš program může postupně snižovat hromady o v tak dlouho, dokud nebude každá hromada menší nebo rovna v, a výsledný počet dělení bude určitě nejmenší možný.
| h |
| v |
| h |
| v |
Jakmile známe maximální počet dělení, tak k němu můžeme přičíst velikost nejvyšší hromady a získáme minimální počet operací úklidu při konkrétní výšce v.
Umíme nyní pro libovolnou výšku nalézt minimální počet operací, nicméně stále nevíme, jaká výška je ta správná. Nemusíme však tuto výšku nějak složitě hledat, stačí vyzkoušet všechny a vybrat takovou, která potřebuje nejmenší počet operací.
Pro každou z řádově N výšek jsme prošli N hromad, takže tato část algoritmu má časovou složitost O(N2).
Zrychlujeme
Nyní máme sice funkční řešení, nicméně je poměrně pomalé. Zkusme jej tedy urychlit optimalizací podúlohy hledání minimálního počtu operací dělení pro danou výšku v.
V kvadratickém řešení jsme získali nutný počet kroků postupným vydělením všech hromad výškou v a následným sečtením všech výsledků.
Ke stejnému součtu lze dojít i s trochu odlišným pohledem. Místo toho, abychom hromady přímo dělili, tak budeme postupně zjišťovat, kolik hromad je třeba rozdělit jednou, dvakrát, třikrát apod. Nahlédneme, že výšky hromad, které potřebují k rozdělení k operací, leží nutně v intervalu [vk+1, vk+v]. Minimální počet operací rozdělení u těchto hromad je potom roven jejich počtu vynásobeném k. Pokud se takto postupně zeptáme na všechny validní intervaly, získáme minimální počet operací nutný k rozdělení hromad pro danou výšku v.
Je třeba vyřešit, jak co nejrychleji zjistit počet hromad v nějakém intervalu. Založíme si pomocné pole, kde hodnota na i-té pozici říká, kolik existuje hromad výšky i. Když nás potom zajímá počet jednotlivých hromad v nějakém konkrétním intervalu, můžeme použít jednoduše prefixové součty.
Zbývá vyřešit, jakou bude mít algoritmus s touto úpravou časovou složitost. Na první pohled by se mohlo zdát, že jsme si příliš nepomohli, když například testujeme v=1, potřebujeme až řádově N dotazů na intervaly. Celkový počet dotazů na intervaly lze vyjádřit takto:
| N |
| v=1 |
| N |
| v |
| N |
| v=1 |
| 1 |
| v |
Zbývající suma je harmonická řada. Pro tu platí, že lze její součet shora omezit logaritmem z počtu prvků, které sčítáme. Celkově tak provedeme O(N log(N)) dotazů na intervaly a taková bude i výsledná časová složitost našeho algoritmu. Paměťová složitost bude O(N), protože si musíme pamatovat pole s prefixovými součty.
Lineární algoritmus
Doposud jsme hledali pro každou možnou maximální výšku minimální počet operací dělení nutný k jejímu dosažení. Co kdybychom místo toho zkusili naopak pro každý rozumný počet dělení nalézt nejmenší maximální výšku, které lze s tímto počtem dosáhnout?
Zkusme si na triviálních případech rozmyslet, jak by takový postup mohl vypadat. Pokud máme k dispozici jedno dělení, tak se nám vyplatí rozdělit největší hromadu přesně v polovině.
V případě dvou dělení se poté nabízí v prvním kroku rozdělit největší hromadu na půl a v dalším kroku rozdělit na půl tu hromadu, která je aktuálně největší. To ovšem nemusí být optimální postup. Pokud druhá rozpůlená hromada byla původně částí první hromady, tak to znamená, že někde v posloupnosti zůstala druhá polovina první hromady a maximální výška se po druhé operaci snížila v nejlepším případě o 1.
| v |
| k |
Vraťme se nyní zpět k případu s dvěma děleními. Pokud v druhém kroku zjistíme, že je největší hromada pozůstatkem hromady rozdělené v předchozím kroku a že je tedy nutné rozdělit původní hromadu na více částí, tak již víme, že se vyplatí rozdělit původní hromadu co nejvíce rovnoměrně. Vezmeme tedy původní operaci rozpůlení z prvního kroku zpět a nahradíme ji rozdělením na třetiny.
Tento postup snadno zobecníme, budeme postupně v jednotlivých krocích navyšovat použitý počet dělení. V každém kroku nejprve zjistíme, jaká hromada je aktuálně nejvyšší, z jaké původní hromady pochází a na kolik částí byla tato původní hromada rozdělena. Původní hromadu poté spojíme dohromady a rozdělíme co nejvíce rovnoměrně na o jedna víc částí.
Pro každý rozumný počet dělení takto spočítáme nejnižší možnou maximální výšku. Přičtením výšky pak pro každý počet dělení získáme minimální počet operací nutných k úklidu a počet operací nejkratšího úklidu získáme jako minimum z těchto hodnot.
Jaké hodnoty dělení vlastně budeme zkoušet? Již víme, že nejkratší úklid musí být menší nebo roven nejvyšší hromadě, takže nemá smysl zkoušet jiný počet dělení než 0 až maximální výška.
Zbývá vyřešit, jak tento algoritmus efektivně implementovat.
Náš program by měl být schopen identifikovat původní hromady, aby byl schopen pracovat s jejich částmi, takže každé hromadě přiřadíme číslo odpovídající pořadí, v jakém jsme ji obdrželi na vstupu. Též je stěžejní umět o každé původní hromadě zjistit, na kolik částí již byla rozdělena. K tomu použijeme obyčejné pole, kde i-tý index říká, na kolik částí je rozdělena i-tá hromada.
V průběhu algoritmu potřebujeme mnohokrát rychle nalézt aktuálně největší hromadu a zároveň musíme umět opětovně slučovat a rozdělovat hromady na menší části. Kdybychom operaci slučování a rozdělování prováděli přímo, tak bychom museli provést v některých krocích nemalé množství operací. Pomůže nám však pozorování, že se vyplatí vždy přímo pracovat pouze s aktuálně největšími částmi původních hromad. Víme totiž, že tato část bude prohlášena za maximum dřív než ostatní části téže hromady a zároveň po jejím zpracování stejně všechny části původní hromady nahradíme za nové, takže jejich uložení nedává smysl.
Jako datovou strukturu k nalezení aktuálního maxima lze použít maximovou haldu, jejíž prvky by kromě výšky obsahovaly informaci o tom, k jaké původní hromadě patří. S obyčejnou binární haldou bychom však dosáhli totožné časové složitosti jako v minulém algoritmu. K rychlejšímu řešení můžeme využít skutečnosti, že mají všechny hromady výšky odpovídající celým číslům velké řádově jako N a že nám aktuální maximum v průběhu algoritmu nikdy nevzroste.
Místo haldy proto můžeme použít obyčejné pole indexované podle výšek hromad. Každý prvek pole potom bude odpovídat seznamu čísel jednotlivých původních hromad, jejichž největší díl má výšku odpovídající indexu. Toto pole budeme procházet odzadu, tedy od nejvyšší výšky. V každém kroku algoritmu zpracujeme jedno číslo ze seznamu, zjistíme jaké hromadě odpovídá a na kolik částí již byla rozdělena. Tuto hromadu rozdělíme na více částí a uložíme novou největší část zpět do pole na odpovídající pozici. V momentu, kdy na nějaké pozici čísla dojdou, posuneme ukazatel o jednu pozici doleva.
Celkově tak zpracováváme O(N) hromad a nejvýše tolikrát i posuneme ukazatel v naší struktuře. Časová složitost tohoto algoritmu bude tedy rovna O(N). Paměťová složitost bude O(N).
 36-3-4 Nejlepší programovací jazyk, část III. (Zadání)
36-3-4 Nejlepší programovací jazyk, část III. (Zadání)
Najděte si šálek čaje či jiného vašeho oblíbeného nápoje, a pojďte s námi studovat taje ksplangu, nejlepšího programovacího jazyka.
V této části jsme se zaměřili na úkoly, které využijí control flow instrukcí pro stavbu cyklů a podmínek. Vnořování cyklů i podmínkám se dokonce dalo kompletně vyhnout, v sekcích pro jednotlivé úkoly si ukážeme hned několik technik pro zjednodušení implementace.
Pro tuto úlohu se vyplatilo ksplangové programy generovat programem v jiném programovacím jazyku, to nám umožňuje opakovaně využívat bloky a zapisovat to snáze.
Pro lepší čitelnost a pochopitelnost budeme ukazovat programy v pseudoksplangu.
Mezi instrukce či sekvence instrukcí budeme do „komentáře“ začínajícím znakem
# zapisovat současný stav zásobníku, aby bylo jasné, co se v programu zrovna
děje. Také budeme používat různé zkratky, podobně jako v předchozím řešení.
Tyto zkratky či funkce jsou v pseudoksplangu barevně zvýrazněny. Normální
instrukce zvýrazněny nejsou. Cykly jsou zvýrazněny ještě jinak a jejich obsah
je obalen složenými závorkami.
V tomto popisu nebudeme nijak optimalizovat na délku programu, naopak se budeme snažit o co nejčitelnější popis konstrukcí.
Přehled zkratek
Budeme používat značení jako
v řešení předchozí části, kde
push(N) značí přidání čísla N na vrchol zásobníku a dup značí
zduplikování čísla (univerzální duplikací z řešení předchozí části), kromě toho
ještě přidáváme několik novinek, například prohazování prvků. Je nám jasné, že
každý z vás má jiné pojmenování a značení, proto doufáme, že pro vás naše
značení bude dostatečně srozumitelné. Předem se omlouváme, pokud něco
parametrizujeme v přesně opačném pořadí než vy.
V popisech také občas nazýváme zásobník s a i-tou hodnotu odspodu zásobníku
s[i].
| Zápis | Popis | Implementace |
push(N) | přidá N na zásobník | záleží na N |
dup | zduplikuje horní číslo na zásobníku | viz předchozí řešení |
dup_ab | zduplikuje dvě horní čísla na zásobníku (a b -> a b a b) | vyrobíme níže v sekci Úkol 2 |
roll(len, dist) | orotuje horních len prvků o dist | push(dist) push(len) lroll |
swap2 | prohodí horní dvě čísla na zásobníku (neplést se swap) | push(1) push(2) lroll, tj. roll(2, 1) |
-- | odečte jedničku | push(-1) push(0) u |
negate | x -> -x | viz předchozí řešení |
load | i -> s[i] | vyrobíme níže v sekci Indexování |
store | a i -> nic, s[i] = a | swap pop |
zero_not | a -> pokud a = 0, tak 1, jinak 0 | vyrobíme níže v sekci Cyklus do while nonzero |
is_-2^63 | a -> pokud a = -263, tak 1, jinak 0 | vyrobíme níže v sekci Úkol 2 |
CS pop
V ksplangu neexistuje žádná instrukce, která by zaručeně neměla žádný efekt.
Existuje hned několik možností, jak si vyrobit sekvenci instrukcí, která
nic nedělá, ale kombinace CS pop je pro vytváření cyklů zdaleka
nejzajímavější. Control flow instrukce totiž neodstraňují své parametry, a
většinou se jich potřebujeme nějak zbavit.
CS pop umístěná na začátku cyklu při vstupu do cyklu nic neudělá, ale
poté nám umožňuje skákat v dalších iteracích na instrukci pop pomocí instrukcí
GOTO či j, a to odstraní právě přebývající parametr.
V případě dvouparametrové instrukce BRZ můžeme použít konstrukci CS CS pop pop
a skákat na první pop. Toto odstraní i hodnotu, s kterou se BRZ porovnávalo.
Díky možnosti provést na konci cyklu duplikaci (nebo CS, které zachovává
nulovost) nám to nikdy nevadí.
Cyklus do while zero
Začneme nejvíce přímočarým cyklem, který je ekvivalentem cyklu do while z mnoha programovacích jazyků horších než ksplang (například C). Kód v tomto cyklu se vždy provede alespoň jednou, a opakuje se, dokud je na vrcholu zásobníku nula.
Tento cyklus je založen na jednom podmíněném skoku BRZ na konci bloku kódu, a
ten bude skákat vždy jen dozadu. Díky tomu lze snadno při vytváření programu na
zásobník umístit index, na který se bude skok vracet, už ho v ten moment totiž
známe. Taktéž to umožňuje snadné vnořování těchto cyklů. Nesmíme zapomenout
těsně před BRZ prohodit horní dva prvky, jelikož potřebujeme, aby index
instrukce byl až pod kontrolovanou hodnotou.
CS
CS
pop
pop
[instrukce v cyklu]
push(index prvního popu)
swap2
BRZ
Všimněte si, že toto odstraní hodnotu, kterou porovnáváme s nulou. Můžeme si ji
na konci našeho vnitřku cyklu zduplikovat, a to buď pomocí standardního dup, nebo dokonce postačí instrukce CS, která zachovává nulovost.
Tento nejjednodušší cyklus stačil k vyřešení všech úloh. Jenom ještě potřebujeme umět znegovat kontrolu nuly.
Cyklus do while nonzero
Stejný jako cyklus do while zero, ale přidáme „negaci“ kontrolovaného čísla.
Z nuly vyrobíme nenulu a z nenuly vyrobíme nulu. Podle toho, co víme o našem
čísle, existuje hned celá řada postupů, které fungují, ale tady si ukážeme jeden
pěkný obecný, který funguje pro libovolné číslo. Jelikož nejde o standardní
negaci, nazvěme tuto funkci například zero_not (pojmenovávání je těžké).
Z čísla x pomocí absolutní hodnoty znaménka vyrobíme nulu, když je nulou,
nebo jedničku, pokud není. Pak použijeme instrukci bulkxor, abychom jej
vyxorovali s jedničkou, což je ekvivalentně negace.
# x
push(5) u
# sgn(x) - znaménko x, zachovává nulovost
push(0) push(1) u
# |sgn(x)| - nula nebo jedna
push(1) push(1)
# |sgn(x)| 1 1
bulkxor
# !|sgn(x)|
Tato negace nuly (zero_not) v reálném ksplangu po drobných
optimalizacích pro zmenšení počtu instrukcí:
cs cs lensum ++ cs lensum ++ ++ ++ u
cs cs funkcia cs ++ u cs j ++ cs
bulkxor
Úkol 1 – Sekvence [3b]
Teď když už máme do while nonzero cyklus, můžeme ho naprosto přímočaře použít.
Připomínáme, že -- je náš zápis pro dekrementaci (opak ++).
DoWhileNonZero {
dup -- dup
}
To je vše. Číslo z druhé duplikace akorát zkonzumuje cyklus pro kontrolu, jestli už má skončit. Ještě si to rozepíšeme. Všimněte si, že s každým cyklem jedno číslo zůstane nalevo od našich pracovních hodnot.
CS CS pop pop
# i
dup
# i i
--
# i i-1
dup
# i i-1 i-1
push(2)
# i i-1 i-1 2
# ^ na index 2 skočí BRZ (první pop)
swap2
# i i-1 2 i-1
# ^ příští i
# ^ na toto už nesáhneme
BRZ
Komplexnější cykly a podmínky
Pojďme se krátce zamyslet nad podmínkami a komplexnějšími cykly, ačkoliv se jim díky trikům dá v následující úloze vyhnout.
Skoro každá složitější konstrukce vyžaduje někdy skákat dopředu. To je poněkud
problematické, protože v moment vytváření absolutního skoku (ať už BRZ
nebo GOTO) ještě nevíme, kolik instrukcí vlastně budeme potřebovat na
push cílového indexu, a právě tuto délku potřebujeme pro spočítání, kam
to vlastně skáčeme.
Naštěstí existuje relativně jednoduché (byť mírně neefektivní) řešení, a to naučit
se vyrábět potřebné push na nějaký velký konstantní počet instrukcí,
nazvěme ho P. Pro jednoduchost si pak můžeme pro celý program zvolit nějaké
velké číslo P, a pak každý problematický push indexu doplnit sekvencí
CS ++ pop s vhodným počtem ++, aby to vyšlo na správnou délku.
Všimněte si, že sekvence CS ++ pop při provedení nic nedělá, a že
umožňuje vyrábět výplň, která má lichý počet instrukcí.
Hledat optimální schéma výplní je těžké, proto doporučujeme pro celý program použít nějakou vhodně velkou konstantu P, a když zjistíte, že nestačí, tak ji zvětšit (o jedna, na dvojnásobek...) a zkusit to znovu. Také nezáleží na tom, jak efektivně umíte vyrábět konstanty, stačí zvolit dostatečně velké P.
Nyní sice umíme push(n) nafouknout na konstantní délku, ale ještě si
musíme rozmyslet, jak toho využít. Máme totiž alespoň 2 možnosti, přičemž
v závislosti na konkrétním řešení může být jedna z nich snazší:
- Spočítat si dopředu délku kódu, což už jde díky tomu, že skoky mají konstantní délku.
- Před skokem si nechat místo na P instrukcí a ty dopsat zpětně, až když známe index, kam skáčeme.
Při zapisování zpětně jde vcelku přirozeně rekurzivně do sebe vnořovat cykly a podmínky.
Podmínka if zero
Pojďme si vyrobit podmínku, která používá instrukci BRZ. Postavíme ji
tak, že bude umět i větev else, která se provede, když horní hodnota není nula.
Jde samozřejmě pouze o jednu z mnoha možných implementací. Jak jsme si popsali
v předchozí sekci, můžeme si připravit konstantní počet instrukcí na push
a poté jej tam doplnit, až když známe správný index. Tato konstrukce
kontrolovanou hodnotu nemaže (na rozdíl od cyklů výše).
# na vrcholu zásobníku je kontrolovaná hodnota
push(index_then)
swap2
BRZ
pop2
push(index_else)
GOTO
pop2
# ^ index této instrukce je index_then
[instrukce pokud je to nula]
push(index_konec)
GOTO
pop
# ^ index této instrukce je index_else
[instrukce pokud to není nula]
CS
pop
# ^ index této instrukce je index_konec
Indexování
Pro oba zbývající úkoly se nám bude hodit umět přistupovat k hodnotám, které jsou
někde na zásobníku, když známe jejich index. To nám umožňuje instrukce swap
(neplést s pseudoksplangovou funkcí swap2).
Nejprve chceme vytvořit funkci load, která index i nahradí s[i], ale zachová na s[i] původní hodnotu. Lze vyrobit i jednodušší
destruktivní verzi, a to někdy může stačit, ale tady si vyrobíme tu obecnější
variantu.
# n
dup
# n n
CS
# n n X - X je dočasná hodnota na s[i]
swap2
# n X n
swap
# n s[n]
dup
# n s[n] s[n]
roll(3, 2)
# s[n] s[n] n
swap
# s[n] X
pop
# s[n]
Opačnou funkci, která uloží hodnotu a na index i nazvěme store. Pro prvky v pořadí a i lze implementovat přímočaře pomocí swap pop, a tuto verzi budeme používat.
Úkol 2 – Řazení [4b]
Tento úkol byl ze všech nejpracnější. Pro vyřešení stačilo naprogramovat libovolný algoritmus na řazení čísel, bez problémů prošlo cokoliv, co mělo kvadratickou časovou složitost, a to i pokud to byla kvadratická časová složitost v nejlepším případě. Například tedy bylo v pořádku bublinkové řazení (bubble sort), které neskončí, když už je seřazeno, ale provede N iterací.
My si tady implementujeme následující třídící algoritmus, který se vyznačuje svou jednoduchostí:
ICan'tBelieveItCanSort(zásobník s, délka n)
- Pro i od 0 do n-1:
- Pro j od 0 do n-1:
- Pokud s[i] < s[j]:
- Prohoď s[i] a s[j]
Pokud nevěříte, že tento algoritmus funguje (například kvůli podezřelému směru nerovnosti), doporučujeme nahlédnout do anglického článku Is this the simplest (and most surprising) sorting algorithm ever? od Stanley P. Y. Funga, z kterého pochází.
Abychom mohli přímočaře použít náš do while nonzero cyklus, potřebujeme otočit směr procházení. Poté také musíme otočit nerovnost, jinak algoritmus začne řadit v opačném pořadí.
ICan'tBelieveItCanSortPozadu(zásobník s, délka n)
- Pro i od n-1 do 0:
- Pro j od n-1 do 0:
- Pokud s[i] > s[j]:
- Prohoď s[i] a s[j]
Základ naší implementace tedy budou dva vnořené cykly do while nonzero od n-1 do 0. Alternativně ale také můžeme využít drobného triku a pořídit si cyklus pouze jeden: od čísla n2-1 do čísla 0. Poté si můžeme dva indexy i, j z hlavního indexu vypočítat:
| i | = index / n |
| j | = index mod n |
Výpočet index mod n můžeme pro kladná čísla provádět jak instrukcí %, tak REM. Nesmíme zapomenout, že dělení v univerzální instrukci u nefunguje přímočaře. Je potřeba nejdříve odečíst výsledek REM, a poté
už dělí normálně. My tuto variantu v tomto řešení dál nebudeme popisovat, ale
může být snazší ji naprogramovat, jelikož nevyžaduje vnoření cyklů.
Pro implementaci prohození budeme potřebovat jednu z následujících dvou věcí:
- porovnávací funkci – stačí nám, aby vracela 0/1 podle toho, zda chceme prohazovat, ale porovnávací funkce, která vrací -1/0/1 podle toho, které číslo je větší, se obecně k programování hodí,
- funkci
min(jakožto opak instrukcemax).
V našem řešení použijeme druhou variantu, tedy funkci min. S tou nemusíme
implementovat žádnou další podmínku, stačí nám vždy přiřadit následující:
| s[i] | = min(s[i], s[j]) |
| s[j] | = max(s[i], s[j]) |
Pro implementaci max existuje instrukce se stejným jménem. Bohužel ale
nemůžeme implementovat min prostým -max(-a, -b), jelikož musíme
podporovat i hodnotu -263 a tu nelze znegovat. Můžeme to ale snadno
vyřešit podmínkou:
min(a, b)
- Pokud a ≠ -263 a b ≠ -263:
- Výsledek je -max(-a, -b)
- Jinak:
- Výsledek je -263
Jak zjistit, jestli číslo x je -263? Nejdříve využijeme toho, že můžeme vždy bezpečně odečíst znaménko čísla a místo toho ověřovat, jestli x-sgn(x) je -263-1. Z toho už můžeme bezpečně vzít absolutní hodnotu, a všimněte si, že jenom pro x = -263 vychází, že |x-sgn(x)| = 263-1, tedy maximální hodnota. Poté už můžeme absolutním rozdílem ověřit, jestli jde o naše hledané číslo, x = -263 právě když ||x-sgn(x)|-(263-1)| = 0. Tento výpočet nikdy nepřeteče díky tomu, že děláme absolutní rozdíl dvou kladných čísel (největší rozdíl tedy může být 263-1).
Implementace funkce is_-2^63 v pseudoksplangu:
# a
dup
# a a
push(5) u
# a sgn(a)
push(1) u
# |a-sgn(a)|
push(2^63-1)
# |a-sgn(a)| 2^63-1
push(1) u
# ||a-sgn(a)|-(2^63-1)|
# 0 pro a = -2^63, nenula pro ostatní
zero_not
# 1 pro a = -2^63, jinak 0
Implementace funkce min v pseudoksplangu:
# a b
dup
# a b b
is_-2^63
# a b b==-2^63
zero_not
# a b b!=-2^63
roll(3, 2)
# b b!=-2^63 a
dup
is_-2^63
zero_not
# b b!=-2^63 a a!=-2^63
swap2
# b b!=-2^63 a!=-2^63 a
roll(4, 1)
# a b b!=-2^63 a!=-2^63
And
# a b b!=-2^63&a!=-2^63
IfZero {
# a b 0
pop pop pop push(-2^63)
# -2^63
} else {
# a b 1
pop
# a b
negate
swap2
negate
# -b -a
max2
# max(-b,-a)
negate
# -max(-b,-a)
}
Pokud nemáte program na generování ksplangu, který zvládá vnořování cyklů či podmínek, tak můžete alternativně využít implementaci minu z následující sekce Podmínka podvodem a implementace minu.
Ještě si pořiďme poslední drobnou funkci, která nám ušetří trochu opakování, a
to duplikaci dup_ab, která zduplikuje dvě čísla po sobě:
# a b
dup
# a b b
roll(3, 2)
# b b a
dup
# b b a a
roll(4, 1)
# a b b a
swap2
# a b a b
A teď, když už máme všechny stavební bloky, můžeme to konečně dát dohromady:
# k
dup
# k k
DoWhileNonZero {
# k i+1
--
# k i
swap2
# i k
dup
# i k k
roll(3, 1)
# k i k
DoWhileNonZero {
# k i j+1
--
# k i j
dup_ab
# k i j i j
dup_ab
# k i j i j i j
load
# k i j i j i s[j]
swap2
# k i j i j s[j] i
load
# k i j i j s[j] s[i]
dup_ab
# k i j i j s[j] s[i] s[j] s[i]
min
# k i j i j s[j] s[i] min(s[j], s[i])
roll(3, 1)
# k i j i j min(s[j], s[i]) s[j] s[i]
max
# k i j i j min(s[j], s[i]) max(s[j],s[i])
swap2
# k i j i j greater lesser
roll(4, 1)
# k i j lesser i j greater
swap2
# k i j lesser i greater j
store
# s[j] = greater
# k i j lesser i
store
# s[i] = lesser
# k i j
CS
# k i j CS(j)
}
# k i 0
pop
# k i
CS
# k i CS(i)
}
# k 0
pop
pop
Pozor, pokud jste naimplementovali load destruktivně, tak se vše rozbije pro
případ, kdy i = j.
Úkol máme hotový, pokud vás zajímají další alternativní způsoby implementace (jedním cyklem, s porovnávací funkcí), tak můžete nahlédnout do Pythonového programu, který přikládáme na konec řešení.
Podmínka podvodem a implementace minu
 Tato sekce není potřeba k vyřešení úlohy, ale ukazuje pěknou techniku.
Doporučujeme přečíst alespoň první odstavec.
Tato sekce není potřeba k vyřešení úlohy, ale ukazuje pěknou techniku.
Doporučujeme přečíst alespoň první odstavec.
Co když se nám nechce implementovat podmínku v předchozím úkolu, zvlášť při
nutnosti ji vnořit do jiného cyklu? Řekněme, že chceme vybrat jednu ze dvou
hodnot x a y, a to podle hodnoty flag, která je nula nebo jednička
(můžeme si ji vyrobit z nuly či nenuly pomocí jednoho či dvou zero_not).
Nabízíme následující trik:
Pokud je flag jedničkou, vyjde x. Pokud je flag nulou, vyjde y. Jediný problém je, že musíme obě hodnoty být schopni vypočítat bez toho, aby došlo k chybě. Nemůžeme to tedy použít, pokud v jednom ze dvou výpočtů může dojít k přetečení, například kvůli hodnotě -263.
Jako příklad použití nabízíme další implementaci funkce min, která vybere menší ze dvou čísel a, b. Nejprve spočítáme instrukcí
m medián z pěti hodnot: a, b, -263, -263, 5. Z toho
vychází jedna z dvou možností:
- číslo 5, pokud obojí a > 5 i b > 5,
- menší z a, b, tedy správná odpověď, ve všech ostatních případech.
Poté můžeme spočítat max(medián, 4) instrukcí max, z toho nám
vyjde číslo 4, pokud šlo o správný výsledek, nebo 5, pokud to správný výsledek
nebyl. Můžeme odečíst 4 a najednou jsme získali nula-jedničkový flag.
Už nám chybí jenom výpočet, který zaprvé nikdy nepřeteče, a zadruhé funguje pro případ, že a > 5 i b > 5. Všimněte si, že od libovolného čísla můžeme vždy bezpečně odečíst jeho znaménko, a tím se přiblížíme o jedna k nule. Bohužel to z čísel -1, 0, 1 vyrobí číslo 0, takže to nelze použít přímočaře. Tady nám to ale stačí, jelikož nás zajímají jenom čísla větší než 5. Po tomto přiblížení můžeme bezpečně otočit znaménka, spočítat maximum, znovu otočit znaménko, a nakonec přičíst jedničku abychom se vrátili zpět od nuly správným směrem. Pro shrnutí, jako druhou možnost vypočteme následující:
A konečně můžeme vypočítat finální minimum z a, b spojením našich dvou výpočtů:
Úkol 3 – Počet čísel na zásobníku [4b]
Úkolem bylo určit počet čísel na zásobníku, a to za předpokladu, že na
zásobníku mohou být libovolná čísla. Kdybychom věděli, že se nějaká hodnota
nebude vyskytovat, tak ji můžeme na konec zásobníku přidat jako tzv. sentinel hodnotu. Pak stačí vyrobit jednoduchý cyklus, který pomocí load
ze sekce Indexování hledá od začátku zásobníku naši sentinel hodnotu, a když ji
najde, tak ví, kolik prvků bylo na zásobníku. Alternativně ji lze umístit na
začátek zásobníku pomocí l-swap a hledat ji pomocí lroll se zvětšujícím
se rozsahem.
Pokud jste zkusili ošálit Odevzdávátko a použili jste nějakou obskurní hodnotu, kterou přece nemůžeme kontrolovat, tak jste brzo objevili, že vám to jen tak neprojde. My jsme totiž zlí a nejdříve jsme vyzkoušeli váš program na malém vstupu, zaznamenali si všechny hodnoty, které kdy byly na zásobníku, a pak jsme pro každou z těchto hodnot vyrobili rovnou dva testy. Nazvěme každou testovanou hodnotu x. První test obsahoval pouze několikrát hodnotu x, což odchytilo většinu pokusů. Druhý test měl první i poslední hodnotu stejnou jako ten malý test, z kterého jsme hodnoty x získávali, proto bychom vaši sentinel hodnotu objevili, i kdyby nebyla konstantní, ale byla nějak vypočítaná z prvního nebo posledního čísla vstupu.
Pro vyřešení s libovolnými hodnotami stačilo udělat akorát jednu drobnou změnu. Pro každý kontrolovaný index můžeme číslo na konci zásobníku vyměnit, a ověřit, že se nezměnilo. Pokud se změnilo, tak už se díváme na prvek, co jsme umístili za pole. Shrňme si náš algoritmus:
Stacklen(zásobník s)
- Pro i od 0 do nekonečna:
- Za zásobník umísti nulu jakožto zarážku
- check1 ← s[i] = 0
- Vyměň nulu za jedničku
- check2 ← s[i] ≠ 0
- Pokud platí obojí check1 a check2:
- Našli jsme zarážku, i je délka zásobníku
Všimněte si, že používáme kontrolu nulovosti, která je o trochu jednodušší než
kontrolovat, že libovolné číslo je jedničkou. Můžeme totiž využít jednu nebo
dvě negace nulovosti zero_not, kterou jsme si už postavili v sekci pro
cyklus do while nonzero. V popisech s[i] == 0 uvažujeme logiku podobnou
jazyku C – znamená to jedna, pokud se s[i] rovná nule, a nula pokud se
nule nerovná.
push(0)
# 0
DoWhileZero {
# i
push(0)
# i 0
swap2
# 0 i
dup
# 0 i i
load
# 0 i s[i]
zero_not
# 0 i s[i]==0
roll(3, 2)
# i s[i]==0 0
++
# i s[i]==0 1
roll(3, 1)
# 1 i s[i]==0
swap2
# 1 s[i]==0 i
dup
# 1 s[i]==0 i i
load
# 1 s[i]==0 i s[i]
zero_not
# 1 s[i]==0 i s[i]==0
zero_not
# 1 s[i]==0 i s[i]!=0
roll(3, 2)
# 1 i s[i]!=0 s[i]==0
And
# 1 i (s[i]!=0&s[i]==0)
roll(3, 1)
# (s[i]!=0&s[i]==0) 1 i
++
# (s[i]!=0&s[i]==0) 1 i+1
pop2
# (s[i]!=0&s[i]==0) i+1
swap2
# i+1 (s[i]!=0&s[i]==0)
}
# len+1
--
# len
A co ksplang dál?
Společně jsme prozkoumali a pokořili některé základní úlohy v ksplangu. Pro psaní komplexnějších programů už teď vše dost zásadně závisí na tom, jaké nástroje jsme si vybudovali. Pokud umíte teď snadno vyrábět cykly a používat recyklovatelné bloky, tak se vám mohou zdát další úlohy snadno dosažitelné. Naopak, pokud jste své programy vytvořili ručně a drží pohromady možná spíše silou vůle, tak psát něco komplikovanějšího může být velmi děsivé. Je čas přenechat prostor dalším úlohám, ale to neznamená, že ksplang přestává existovat.
Pokud jste si ksplang zamilovali, tak pro vás nabízíme hned několik věcí:
- Na našem Discordu naleznete
(alespoň dočasně) nový kanál
#ksplang, kde můžete s ostatními o ksplangu diskutovat. Můžete se podělit o své konstrukce, co jste vymysleli, a tak dál. - V brzké době se v Kurzu na webu objeví ksplangová větev s několika bonusovými úlohami (ještě jsme pořádně nepoužili všechny instrukce!).
- V ksplangu můžete řešit opendata úlohy! Pokud nevíte čím začít, nabízíme například 36-Z3-1 (vstup jsou čísla), a 36-Z3-3 je pěkná úloha s textovým vstupem. U obou jsme ověřili, že jsou řešitelné i v ksplangu.
- V další sekci najdete odkaz na zdrojové kódy ksplangu a také lokální interpreter, můžete si tak ksplang spouštět lokálně.
Zdrojový kód ksplangu a lokální interpreter
Zdrojové kódy našeho interpreteru naleznete na GitHubu.
Programy
Jako součást řešení nabízíme Pythonový program, který umí generovat ksplang včetně vnořování cyklů a podmínek.
Pokud ještě máte v plánu experimentovat s ksplangem, tak zvažte, nakolik si chcete prozradit, co vše je možné. Součást zábavy při psaní ksplangu je totiž si něco takového vytvořit, a také objevovat nové techniky. Můžete ho použít, můžete jenom nahlédnout pro inspiraci, a nebo jej vůbec neotevírat, necháváme to na vás.
Generátor ksplangu pro všechny úkoly (Python 3)
 36-3-X1 Výlet do Japonska (Zadání)
36-3-X1 Výlet do Japonska (Zadání)
Uvažme vhodný graf …
Nevíme si se složitou úlohou rady? První medvědí univerzální rada říká: „Tak si ji zjednodušte!“ Přesně to uděláme: Je dána množina známých slabik α1,… ,αQ a slovo σ. Chceme zjistit, zda slovo σ umíme vyslovit – tedy zda ho lze rozkrájet na podřetězce, které patří mezi známé slabiky.
Pořád nevíme, co s tím? Druhá medvědí univerzální rada napovídá: „Sestrojte si vhodný graf!“. Tedy dobrá: Pro slovo σ= x0… xℓ-1 si pořídíme graf s vrcholy 0 až ℓ, které odpovídají místům, kde jde slovo σ rozříznout: vrchol 0 odpovídá začátku slova, vrchol ℓ řezu na konci, obecně vrchol i řezu mezi znaky xi-1 a xi.
Hrany grafu budou orientované: z vrcholu i povede hrana do vrcholu j právě tehdy, když mezi těmito dvěma řezy leží známá slabika.
Například pro slovo kopriva a slabiky ko, op, pri, riv, va
bude graf vypadat takto:

Rozkrájení slova na známé slabiky pak odpovídá cestě z vrcholu 0 do vrcholu ℓ. Cestu najdeme obyčejným prohledáním grafu do hloubky nebo do šířky. (Kdybychom chtěli nejdelší či jinou speciální cestu, mohli bychom využít toho, že graf je acyklický, a použít indukci podle topologického uspořádání, ale tady nám stačí pouhá existence cesty.)
Zbývá ukázat, jak graf efektivně sestrojíme. Všechny známé slabiky uložíme do písmenkového stromu (neboli trie). Připomeneme si, že vrcholy trie odpovídají prefixům (začátkům) slabik a označené jsou ty vrcholy, kde nějaká slabika končí. Jistě bychom mohli pro každé 0≤ i≤ j≤ ℓ vyhledat v trii slovo xixi+1… xj-1 a pokud vede do označeného vrcholu, vytvořit hranu ij.
To je ale zbytečně pomalé: stačí si všimnout, že pro pevné i a postupně zvyšované j hledáme v trii slovo xixi+1… xℓ-1 a každý navštívený vrchol odpovídá jedné hodnotě j. Pro každé i tedy projdeme jednu cestu v trii a kdykoliv navštívíme označený vrchol, přidáme hranu.
Rozebereme časovou složitost. Nechť Q je počet slabik a M omezení na délku slova i všech slabik (tedy ℓ≤ M). Pak konstrukce trie trvá O(QM), vytvoření grafu O(ℓ2)⊆ O(M2) a prohledání grafu O(M2) [zde využíváme toho, že graf nemá víc než (M+1)2 hran]. Celkem je to O(QM + M2). Podle zadání je Q≫M, takže odhad můžeme zjednodušit na O(QM).
Původní úloha
Co je v původní úloze jinak? Především nemáme skládat jedno slovo, ale hned N různých slov. To ale není problém – místo jednoho grafu jich budeme mít víc, každý graf prohledáme nezávisle na ostatních a spočítáme, v kolika z nich existuje cesta.
Ovšem původní úloha je navíc online: slabiky přibývají postupně a pokaždé máme ohlásit, kolik ze zadaných slov z nich už jde složit. V řeči grafů nám tedy postupně přibývají hrany a chceme si umět všimnout, kdykoliv v nějakém grafu začne existovat cesta z počátečního do koncového vrcholu.
Zaměřme se na jeden graf. Budeme si udržovat označené ty vrcholy, které už jsou dosažitelné z počátečního. Na počátku výpočtu graf nemá žádné hrany, takže je označený jen počáteční vrchol. Kdykoliv nám někdo přidá nějakou hranu uv, podíváme se, zda u a v byly označené. Pokud u nebylo, přidání hrany žádné značky nezmění. Pokud u bylo a v bylo, také se nic nezmění. Ale v případech, kdy u bylo a v nebylo, stane se dosažitelným z počátku jak v, tak všechny vrcholy z něj dosažitelné. Ty objevíme prohledáním grafu z v, přičemž nebudeme zacházet do už označených částí grafu.
Všimněte si, že má-li graf n vrcholů a postupně přidáme m hran, zpracujeme je dohromady v čase O(n+m), protože prohledávání grafu každou hranou projde celkem nejvýše jednou. V našich grafech je n∈O(M) a m∈O(M2), takže O(n+m) ⊆ O(M2).
Ještě potřebujeme vyřešit, jak se dozvídat, které hrany přibyly. K tomu nám opět pomůže trie. Na počátku bude obsahovat jenom kořen. Pak pro každé slovo spustíme algoritmus na stavbu grafu, ale místo aby se díval na značky ve vrcholech trie a podle toho vytvářel hrany, bude do vrcholů trie jenom přidávat poznámky typu „až bude tento vrchol trie označený, vytvoř v tomto grafu tuto hranu“. Jestliže algoritmus bude v trii chtít jít po hraně, která ještě neexistuje, tak ji vytvoří spolu s novým vrcholem.
Po zpracování všech slov tedy vznikne N grafů bez hran a jedna trie – její vrcholy budou odpovídat všem podslovům zadaných slov a budou v nich umístěny instrukce na výrobu hran. Stavba trie potrvá O(M2N), jelikož jsme N-krát spustili algoritmus na výrobu grafu – sice upravený, ale složitost má stále stejnou.
Pak začneme přidávat slabiky. Každou slabiku zkusíme najít v trii. Pokud jí neodpovídá žádný vrchol (cesta pokračuje po neexistující hraně), nepřibude žádná hrana. Pokud dojdeme do vrcholu, podíváme se, jaké hrany grafů jsme si k němu poznamenali, a všechny přidáme. Kdykoliv jsme v nějakém grafu nově označili koncový vrchol jako dosažitelný, zvýšíme o 1 celkový počet sestavitelných slov.
Vrchol v trii pokaždé najdeme v čase O(M), za všechny slabiky dohromady to bude O(QM). A jak už víme, všechna přidání hran do jednoho grafu trvají celkově O(M2), ve všech grafech tedy O(M2N).
Zbývá sečíst složitost všech částí algoritmu. Stavba trie trvá O(M2N), nalezení všech slabik O(QM), přidání všech hran O(M2N). To je celkem O(M2N + QM). To už dále nezjednodušíme: z relací v zadání neplyne mezi MN a Q žádná nerovnost.