První série třicátého šestého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Dostává se k vám první číslo hlavní kategorie 36. ročníku KSP.
Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.
Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.
Odměny & na Matfyz bez přijímaček
Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.- Termín série: neděle 5. listopadu 2023 ve 32:00 (tedy další ráno v 8:00)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak sepsat řešení: viz Návod na teoretické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
- Odměna série: Sladkou odměnu si vyslouží ten, kdo odešle originální řešení úlohy Nejlepší programovací jazyk.
Zadání úloh
- 36-1-1: Strom v zrcadle
- 36-1-2: Taneční
- 36-1-3: Výšlap
- 36-1-4: Mediánový filtr
- 36-1-5: Nejlepší programovací jazyk, část I.
- 36-1-S: Seznámení se s lineární regresí
- 36-1-X1: Mezigalaktická kandidátka
 36-1-1 Strom v zrcadle (9 bodů)
36-1-1 Strom v zrcadle (9 bodů)
„Zrcadlo, zrcadlo, řekni mi, kdo je na světě nejsymetričtější?“ nakrucoval se pěkně košatý král binárních stromů před zrcadlem ve své lesní říši. Všemi svými listy i vnitřními vrcholy věřil, že zrcadlo samozřejmě označí jeho jako největšího a zajisté i nejsymetričtějšího vládce stromů.
Problém byl v tom, že zrcadlo bylo pravdomluvné… a vážně si nebylo jisté ani v tom, jestli je král strom vůbec symetrický. Pomůžete zrcadlu?
V zrcadle se odráží obraz zakořeněného binárního stromu a v každém jeho vrcholu se nachází nějaká hodnota. Stromy mohou vypadat třeba jako na následujícím obrázku.
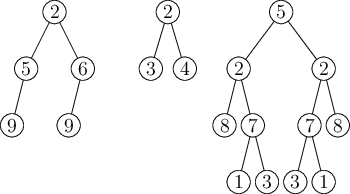
Můžeme si představit, že máme strom uložený v paměti, a to tak, že v každém vrcholu máme ukazatele na levého syna, pravého syna a na otce. Každý z těchto ukazatelů může být i prázdný, pokud vrchol daného syna nemá (prázdný ukazatel na otce pak bude jen v kořeni stromu). Pokud některým pojmům o stromech nerozumíte, můžete nahlédnout do přiložené kuchařky základních algoritmů.
Pro takto zadaný strom by nás zajímalo, jestli můžeme strom ozrcadlit a dostat tak stejný strom – strom se stejným tvarem i stejnými hodnotami ve vrcholech. Ozrcadlení znamená, že pro každý vrchol otočíme pořadí synů (prohodíme levého syna za pravého syna, včetně všeho navázaného pod nimi). Když ozrcadlíme stromy z prvního obrázku, dostaneme následující stromy.
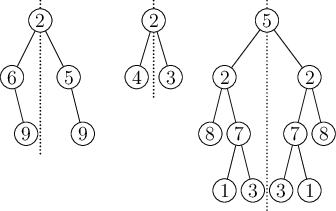
Vidíme, že první strom se po ozrcadlení liší tvarem i hodnotami ve vrcholech, druhý má sice stejný tvar, ale liší se hodnotami ve vrcholech a jen třetí lze ozrcadlit a získat tak stejně vypadající strom. Jen o třetím stromu tedy můžeme prohlásit, že je symetrický.
Zrcadlo bohužel nemá moc velkou výpočetní paměť, umí si pamatovat jen konstantně mnoho údajů. Pozor, zásobník rekurze se také počítá do paměti, takže si určitě nemůžeme dovolit rekurzivní funkci na procházení stromu.
Vymyslete a popište algoritmus, který za těchto paměťových omezení bude umět pro již načtený strom v paměti v co nejrychlejším čase rozhodnout, zdali je symetrický. Porovnání dvou hodnot ve vrcholech zvládneme v čase O(1).
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-1-2 Taneční (11 bodů)
36-1-2 Taneční (11 bodů)
Král pořádá veliký ples, na kterém se sešlo mnoho úžasných tanečníků a tanečnic. Právě probíhá dámská volenka – dámy i pánové stojí naproti sobě ve dvou stejně početných řadách: N dam a N pánů. Pro jednoduchost jsou obě řady očíslované popořadě čísly 1 až N.
Dámy se už před začátkem dámské volenky dohodly na tom, kterého z pánů si každá dáma vybere pro následující tanec – každá si vybrala jiného, takže všechny dámy i všichni pánové jsou pro tento tanec zadaní.
Jak začne hrát hudba, tak se dámy mohou vydat ke svým vybraným partnerům. Problém je ale v tom, že se dráhy dam mohou křížit, například když si první dáma vybere druhého pána a druhá dáma toho prvního. A to by mohlo způsobit faux-pas.
Některé dámy tak budou muset chvíli počkat. Rády by ale věděly, kolik nejvýše dam bude moci vyrazit hned, jak začne hrát hudba, aby se dráhy žádných dvou z nich nekřížily. Pomůžete jim?
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku vstupu bude číslo N udávající počet dam a počet pánů. Na dalších N řádcích pak bude vždy jedno číslo od 1 do N udávající, kterého pána si vybrala i-tá dáma.
Formát výstupu: Na první řádek výstupu vypište jedno číslo K udávající počet dam, které mohou vyrazit bez toho, aniž by se jejich dráhy křížily. Na dalších K řádcích pak uveďte čísla těchto dam. Pokud existuje více způsobů, jak může vyrazit K dam najednou, vyberte libovolný z nich.
10 3 5 2 10 4 1 6 8 9 7
5 1 2 7 8 9
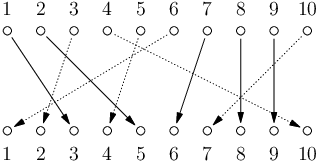
V příkladu výše by ještě stejné dobré řešení bylo vybrat dámy 1, 5, 7, 8 a 9 nebo 3, 5, 7, 8 a 9, všechny ostatní možnosti nedovolí vybrat více než čtyři dámy najednou.
 36-1-3 Výšlap (12 bodů)
36-1-3 Výšlap (12 bodů)
Kristýna se vydala na týdenní turistiku do Jeseníků. Jeseníky si můžeme představit jako 2D mřížku R × S políček, kde na každém políčku je výška terénu.
A jak probíhá Kristýnin den? Nejprve se probudí a vyleze na nějaký kopec, kde si dá oběd (ten má již uvařený a nese si ho s sebou). Po obědě sleze na vyhlídnuté místo, kde si rozloží spacák a bude před spaním sledovat hvězdy.
Dneska má k obědu borůvkové knedlíky, což je do žaludku těžké jídlo, a proto se rozhodla naplánovat dnešní výšlap následujícím způsobem:
- Ráno se probudí na místě, kde včera večer ulehla.
- Poté, plná energie, vyleze na kopec. Bude se opakovaně pohybovat na sousední políčka (políčka v Jeseníkách sousedí stranou, roh nestačí) a vždy se musí pohnout na vyšší, než to na kterém stojí.
- V nejvyšším bodě výšlapu si dá borůvkové knedlíky.
- Poté, plná knedlíků, půjde rovnou dolů. S knedlíky se špatně chodí do kopce, a proto každé další pole musí být nižší než předchozí.
Kristýna by chtěla poznat co nejvíce krás Jeseníků, a proto by její výšlap měl být co nejdelší (co do počtu polí). Políčko je možné navštívit během výšlapu cestou nahoru i dolů, pak se do délky započítává každé jeho navštívení. Pokud je nejdelších výšlapů více, pak vyberte ten s nejvyšší navštívenou výškou (dá se tam fotit pěkné panorama).
Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.
Formát vstupu: Na prvním řádku dostanete dvě čísla R a S – počet řádků a sloupců mapy Jeseníků. Na druhém řádku dostanete čtyři čísla Sx, Sy, Cx, Cy – souřadnice startu a cíle výšlapu (souřadnice x udává sloupec, souřadnice y řádek; indexujeme od nuly s tím, že políčko v levém horním rohu má souřadnice (0, 0)). Následuje R řádků, kde na každém z nich je S čísel popisujících Jeseníky – číslo udává výšku terénu na daném políčku.
Formát výstupu: Na první řádek vypište délku nejdelšího výšlapu L. Potom vypište L řádků, na každém Xi, Yi – souřadnice i-tého políčka výšlapu. První políčko musí být Sx, Sy a poslední Cx, Cy. Pokud je nejdelších výšlapů více, pak vypište ten s nejvyšší navštívenou výškou. Pokud je stále výšlapů více, vypište libovolný z nich. Zaručujeme, že nějaký výšlap vždy existuje.
4 3 1 0 1 3 1 1 1 1 6 1 9 7 1 1 1 1
6 1 0 1 1 1 2 0 2 1 2 1 3
 36-1-4 Mediánový filtr (12 bodů)
36-1-4 Mediánový filtr (12 bodů)
Byl pozdní večer a astronom pracující s výstupy z JWST (James Webb Space Telescope) si po pátém pádu jeho oblíbeného grafického programu uvědomil, že složený obrázek z teleskopu o rozlišení dosahujícím gigapixelové velikosti asi takhle jednoduše neodšumí. Posadil se tedy ke klávesnici a začal přemýšlet o tom, jak napsat vlastní program.
Má čtvercový obrázek o velikosti N×N pixelů a rozhodl se použít mediánový filtr o velikosti K×K na odstranění impulzního šumu. Uvažujme pro jednoduchost, že obrázek je jen ve stupních šedi (v rozsahu od nuly do nějakého vysokého čísla) a K bude vždy liché (aby čtverec K×K měl vždy jasně určený střed).
Mediánový filtr funguje tak, že pro každý pixel obrázku umístí do tohoto pixelu střed čtverce a z až K2 hodnot ve čtverci (méně hodnot tam může být například na okrajích obrázku) vybere tu prostřední, neboli medián, a tu zapíše do výsledného obrázku. Tím dojde třeba k odstranění náhodně „přepálených“ pixelů.
Počítejte s tím, že 1 ≪ K ≪ N (K je řádově větší než malá konstanta a zároveň řádově menší než N). Počítat mediánový filtr pro každý pixel obrázku tak nedává moc smysl, protože by výpočet běžel moc dlouho. Tato úloha cílí na řešení v čase určitě lepším než Θ(N2K2).
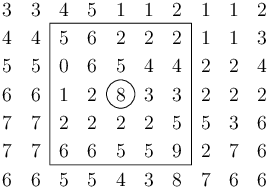
V příkladu výše vidíte mediánový filtr pro K=5, který právě počítá, co bude v novém obrázku na pozici zakroužkovaného pixelu. Má okénko s 25 hodnotami, které když si seřadíme, tak to jsou: 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 8, 9. Medián (a tedy výsledná hodnota) je číslo 4.
Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.
 36-1-5 Nejlepší programovací jazyk, část I. (1 bod)
36-1-5 Nejlepší programovací jazyk, část I. (1 bod)
Jak bylo vyzkoumáno už dávno [1], dobrý programovací jazyk lze vytvořit přidáním samých dobrých instrukcí. Pojďme tedy spolu uvařit ten nejlepší programovací jazyk.
Upozornění: Toto není kuchařková úloha.
Náš programovací jazyk počítá s celými čísly (jak je už z názvu zřejmé, jsou lepší než čísla necelá). Jediná paměť, kterou má k dispozici, je zásobník. Ten si můžete představit jako posloupnost čísel uspořádanou shora dolů. Nová čísla přidáváme na vrchol zásobníku, odebíráme opět z vrcholu.
Celá čísla jsou 64-bitové znaménkové integery (tedy rozsah od -263 až po 263-1). Přetečení způsobí ukončení programu chybou. Zásobník má prozatím přesně nespecifikovaný maximální počet prvků (alespoň 100 000), při přeplnění dojde k ukončení programu chybou. Taktéž existuje prozatím blíže nespecifikovaný limit na čas výpočtu.
Program se skládá z konečné sekvence instrukcí zapsaných do souboru. Kromě zásobníku ještě máme instrukční ukazatel IP, což je číslo příští vykonávané instrukce. Začíná na 0, tedy na první instrukci, a když přesáhne číslo poslední instrukce, tak program skončí. Ale než se dostaneme k programování, musíme nejdřív sehnat ty nejlepší instrukce.
Úkolem každého z vás bude odevzdat popis jedné vámi vymyšlené instrukce a její očekávaný zápis. Pokud nespecifikujete jinak, instrukce přičte k IP jedničku. Také nám dejte vědět, jestli chcete svou instrukci zadat anonymně, nebo jestli se chcete podepsat – v takovém případě vás u ní pak uvedeme jako autora.
Příklad: instrukce + sečte dvě čísla na vrcholu zásobníku a nahradí je
jejich součtem.
Instrukce rozhodně nemusí být tak přímočaré jako sčítání, nebojte se popustit uzdu fantazii. Požadujeme pouze, aby bylo chování instrukce jednoznačné a šlo ji rozumně implementovat. Pokud si nejste jistí, napište nám. Instrukce může být netriviální, ale upozorňujeme, že výpočetně příliš náročné instrukce mohou zabrat příliš času vykonávání programu, který je omezený.
Pro inspiraci se můžete také podívat na úlohu 35-4-1 Golfový turnaj.
Druhou část úlohy očekávejte v druhé sérii. A také prosím o této úloze nediskutujte na Discordu ani jinde (ať nezkazíte ostatním vymýšlení originálních instrukcí).
Zdroje
[1] ČAPEK, Josef. Povídání o pejskovi a kočičce. 16. vyd., Praha: Albatros, 2003. 118 s. Strana 79.
 36-1-X1 Mezigalaktická kandidátka (10 bodů)
36-1-X1 Mezigalaktická kandidátka (10 bodů)
Toto je bonusová úloha pro zkušenější řešitele, těžší než ostatní úlohy v této sérii. Nezískáte za ni klasické body, nýbrž dobrý pocit, že jste zdolali něco výjimečného. Kromě toho za správné řešení dostanete speciální odměnu a body se vám započítají do samostatných výsledků KSP-X.
Galaktickou říši čekají další volby! Jednotlivé členské rasy mezigalaktické unie už předložily císařskému úřadu své seznamy kandidátů, ale císař se teď rozhodl, že v nadcházejících volbách chce, aby na kandidátních listinách jednotlivých ras byla zastoupena všechna pohlaví dané rasy rovnoměrně (což je triviální u ras s jedním pohlavím, ale některé rasy s desítkami různých pohlaví způsobily úředníkům císařského úřadu pořádné vrásky).
Aby to nebylo tak jednoduché, tak úředníci nesmějí nijak přehazovat pořadí navržených kandidátů, jen mohou ze začátku a z konce kandidátních listin nějaký počet kandidátů vyškrtnout tak, aby zůstal co nejdelší úsek kandidátů, ve kterém jsou všechna pohlaví dané rasy zastoupena stejným počtem.
Vaším úkolem je tedy vymyslet algoritmus, který pro zadaný počet pohlaví K a pro posloupnost délky N sestávající se z pohlaví kandidátů 1 až K odstraní co nejméně kandidátů ze začátku a konce tak, aby úsek, který zbude, byl vyrovnaný.
Nápověda
Protože se nikomu nepodařilo tuto úlohu vyřešit, rozhodli jsme se, že prodloužíme její deadline do konce 2. série. Navíc vydáváme následující nápovědu, která vám snad pomůže k řešení.
Očekávaná časová složitost je
Toho lze dosáhnout třeba metodou Rozděl a panuj s podproblémy o menším počtu pohlaví.
 36-1-S Seznámení se s lineární regresí (15 bodů)
36-1-S Seznámení se s lineární regresí (15 bodů)
Letošním ročníkem vás bude provázet seriál. V každé sérii se objeví jeden díl, který bude obsahovat nějaké povídání a navíc úkoly. Za úkoly budete moci získávat body podobně jako za klasické úlohy série. Některé úkoly budou programovací, nicméně pokud nebude řečeno jinak, tak se nebudou vyhodnocovat přes odevzdávátko. Všechny soubory nahrávejte v jednom zazipovaném souboru. Všechny programovací úlohy prosíme řešte v programovacím jazyce Python 3. Abyste se mohli zapojit i během ročníku, seriál bude možné odevzdávat i po termínu za snížený počet bodů. Vzorové řešení seriálu proto před koncem celého ročníku KSP uvidí jen ti, kdo už seriál odevzdali.
V letošním seriálu se zaměříme na praktické téma, které využívá znalosti z pravděpodobnosti, matematické analýzy a lineární algebry. Tento rok se budeme věnovat strojovému učení (anglicky machine learningu). Buzzwordy jako machine learning, neural networks, ChatGPT či jen AI se v průběhu posledních let dostaly do popředí a spoustu lidí o tomto tématu mluví, i když většina o něm neví téměř nic.
V tomto seriálu se nestihneme dostat tak daleko, abychom si pověděli, jak funguje ChatGPT či jiní chatovací boti, ale ukážeme základní stavební bloky, od kterých se současné nejpokročilejší techniky v umělé inteligenci odvíjejí.
Než se dostaneme k samotnému strojovému učení, tak si nejdříve povíme, co si pod tímto pojmem vůbec představujeme. O nějakém programu (ve strojovém učení programům říkáme modely) můžeme říct, že se učí, pokud se s přibývajícím množstvím dat, kterými jej krmíme, zlepšuje v nějaké metrice. Je důležité poznamenat, že úspěšnost strojového učení měříme nikoliv na těch datech, kterými model krmíme, ale na dosud neviděných datech. Tím se strojové učení zásadně liší od databází či optimalizačních úloh jako třeba problém obchodního cestujícího.
Typy úloh
Úloh, které bychom strojovým učením chtěli řešit, je spoustu. Například odšumění obrázku, generování obrázku dle zadání či odpověď na položenou otázku. To jsou už celkem náročné úlohy, takže začneme s něčím jednodušším – regresí a klasifikací. Slovo regrese může znít učeně, ale prakticky to znamená, že budeme odhadovat nějaké číslo. Můžeme si představit, že jsme majitel obchodu s koloběžkami a chceme odhadnout kolik koloběžek půjčíme daný den, když víme, že to bude sobota v lednu a bude 10 °C přes den. Nebo manažer callcentra a chceme vypredikovat kolik lidí zavolá na naši linku.
V úlohách na klasifikaci předpovídáme skupinu. Například před sebou máme obrázek zvířete a chceme určit, o které zvíře z daného seznamu se jedná.
Výkonnost
Pro měření výkonnosti (či chybovosti) potřebujeme nějakou metriku (chybovou funkci), která bude říkat, jak moc dobré či špatné řešení jsme vyprodukovali. Jedna z takových metrik může být průměr čtverců (anglicky mean squared error – MSE). Tato metrika je jednoduchá: pro sadu vstupů (dat) jsme vyprodukovali predikce. Pro každý vstup pak vypočítáme chybovost pomocí formule (p - t)2, kde p je naše predikovaná hodnota a t je ta správná hodnota, kterou chceme odpovědět. Tyto chyby poté zprůměrujeme a to je naše výsledná metrika MSE.
Když však chceme klasifikovat do tříd, typicky budeme chtít používat jinou metriku na měření výkonosti než průměr čtverců. Standardním způsobem, jak měřit správnost modelu při klasifikaci do dvou či více tříd, je přesnost (accuracy). Ta nám říká, jaký podíl dat jsme zařadili do té správné kategorie.
Dále existuje mnoho dalších metrik. Při trénování klasifikačních modelů se ještě potkáme s NLL (negative log likelihood), dále se čast používá f1-skóre, nebo preciznost (precision) či senzitivita (recall), které se mimo strojové učení používají například u lékařských testů, a mnoho dalších.
V dnešním dílu seriálu budeme ale používat jen metriku MSE.
Zkušenosti
V reálném životě se můžeme učit (dostávat zkušenosti) různými cestami. Když jsme byli malí, tak nás rodiče učili jména různých předmětů a zároveň nás opravovali, když jsme řekli nějakou blbost. Tomuto typu učení se říká učení s učitelem (supervised learning). Neboli máme sadu dat a ke každému datu známe správnou odpověď, kde jedno dato je jeden příklad (vzorek) ze vstupních dat.
Druhý typ učení je zpětnovazební (reinforcement learning). To známe také z reálného života – naučíme se na test z nějakého předmětu, napíšeme ho a to, zda jsme se naučili dostatečně, zjistíme ze známky. Neboli máme nějakého agenta v nějakém prostředí a ten může dělat nějaké akce a po jedné či více akcí dostaneme zpětnou vazbu (feedback), jak si agent vede.
Poslední typ učení je nejvíce zvláštní, říká se mu učení bez učitele (unsupervised learning). Tento typ učení funguje tak, že programu dáme data a ten má vydat nějaký výsledek. V praxi se tento typ učení používá, když máme data a chceme z nich něco „vykoukat“ (neboli analyzovat data). Tento přístup se používá např. na clusterizaci – máme data a program má vydat nějaké shluky dat, které jsou si podobné. Je očividné, že v závislosti na tom, jakou máme metriku na porovnávání dat, se výstupy můžou razantně lišit.
Další možné využití je např. detekce anomálií. Uvažte, že máte data síťové komunikace ze své sítě a chcete v reálném čase zjišťovat, jestli se ve vaší síti neděje něco nekalého.
Pro začátek začneme s učením s učitelem, ale později v seriálu si ukážeme i nějaký algoritmus, který používá učení bez učitele.
Lineární regrese
Řekli jsme si trochu obecných informací o strojovém učení a nyní si zkusme vyřešit první úlohu. Máme data, kde každé dato má jednu známou hodnotu (featuru). Uvažte, že jste realitní makléř a jediné, co víte o domu, je celková obyvatelná plocha. Chcete znát orientační cenu domu, kterou vám nikdo neřekne. Každý přece chce nakoupit za levno a prodat za draho.
Máte pár dat, kde znáte celkovou obyvatelnou plochu a cenu nemovitosti v inzerátu. Tato data jsou zakreslena jako modré body. Na x-ové ose je celková obyvatelná plocha a na y-ové ose je cena nemovitosti. Cíl je vygenerovat pro každou x-ovou hodnotu predikci – y-ovou hodnotu.
Očekáváme, že body jsou lehce zašuměné, protože všechna měření v reálném světě jsou nějak zašuměná. Zde si to můžete představit tak, že cena v inzerátu není fixní a pokud je dlouhodobě jen jeden zájemce, může kupující snížit cenu. Naopak pokud je hodně zájemců, mohou se předhánět, kdo nabídne více.
Naším cílem je vyprodukovat zelenou čáru, která předpovídá y-ové hodnoty (cenu nemovistosti) pro libovolnou x-ovou hodnotu (celkovou obyvatelnou plochu).
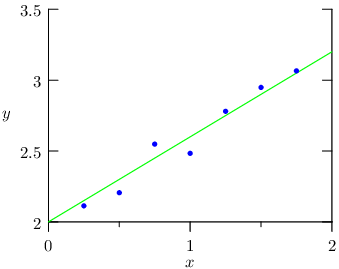
Tento graf je specifický pro jednu hodnotu. Kdybychom měli dvě featury, pak výsledná predikce odpovídá nějaké rovině v trojrozměrném grafu. Tedy by nám někdo o domu řekl další informaci, např. kolik záchodů se v něm nachází. Obecně, predikce je nějaká nadrovina v n-rozměrném prostoru.
Náš první model, který se bude jmenovat lineární regrese, funguje následovně. Mějme vstupní data a každé dato bude mít f featur x1, x2, …, xf.
Když si vezmeme předchozí příklad s realitním makléřem, první featura bude celková obyvatelná plocha, další featury můžou být den v týdnu, kdy se nemovitost prodávala a poslední počet místností v domě. Dále každé dato bude mít i další hodnotu s odpovědí, kterou chceme vypredikovat. Asi nejjednodušší způsob predikování výsledných dat, který by nás mohl napadnout, je vynásobit vstupní hodnoty vhodnými konstantami a sečíst je. A přesně tohle dělá i lineární regrese.
kde w1, w2, …, wf jsou ony konstanty (váhy), které se budeme snažit naučit, aby predikce byla co nejlepší. Tedy chceme váhy minimalizující naší chybovou funkci. Takto uvedená predikce má však jeden problém. Na dato, které má všechny hodnoty x1, x2, …, xf nulové, vypredikujeme vždycky také nulu. Abychom vyřešili tento problém, budeme přičítat ještě jednu hodnotu b, kterému říkáme bias. S biasem vypadá predikce následovně:
Většinou se dělá malý trik: aby se bias nemusel explicitně zapisovat, tak se do vstupních dat přidá ještě jedna featura, která bude mít vždy hodnotu 1. Tím pádem se bias může zahrnout do vah a predikce vypadá skoro stejně jako výše (jen přibyla jedna váha):
kde xf+1 = 1 a wf+1 = b.
Když budeme znát hodnoty w1, w2, …, wf+1, bude již možné predikovat vysněné hodnoty, jak si můžete sami vyzkoušet v následující úloze.
Úkol 1 – Predikce lineární regrese [3b]
Naprogramujte v Pythonu predikci lineární regrese.
Na prvním řádku vstupu dostanete dvě čísla N a F, kde N je počet dat a F je počet featur. Na následujícím řádku naleznete F+1 desetinných čísel reprezentujících váhy modelu, kde poslední z nich je bias. Poté na dalších N řádcích dostanete na každém řádku F desetinných čísel, kde každý řádek reprezentuje jedno vstupní dato.
Vypište N řádků, kde na každém řádku bude jedno číslo (predikce pro dané vstupní dato).
2 3 0.1 1.2 -0.5 3.0 17.0 1.0 0.4 27.0 2.0 0.8
5.7 7.7
Nyní máme vypredikovaná data a nabízí se otázka – jak dobrá jsou?
Jak už víme z předchozí části, k tomu máme chybovou funkci – metriku, která nám říká, jak moc špatná data jsme vypredikovali. Tedy čím větší hodnota chybové funkce, tím hůře. Pro lineární regresi tou chybovou funkcí, kterou budeme používat, bude MSE.
Úkol 2 – Měření chyby [3b]
Napište Pythoní program, který pro zadané váhy a vstupní i výstupní data zjistí, jaká je hodnota chybové funkce MSE pro data vypredikovaná s danými váhami.
Formát vstupu je velmi podobný tomu předchozímu. Na prvním řádku vstupu dostanete dvě čísla N a F, kde N je počet dat a F je počet featur. Na následujícím řádku naleznete F+1 desetinných čísel reprezentující váhy modelu, kde poslední z nich je bias. Poté na dalších N řádcích dostanete na každém řádku F+1 desetinných čísel. Každý z řádku odpovídá jednomu datu – prvních F hodnot na řádku jsou hodnoty jednotlivých vstupních featur a (F+1)-ní hodnota odpovídá správné výstupní hodnotě pro dané dato. Tedy oproti předchozímu případu dostáváme na každém řádku ještě správnou vstupní hodnotu.
Na výstup vypište jediné číslo – hodnotu MSE.
Doporučujeme při implementaci využívat kusů kódu z předchozího úkolu.
2 3 0.1 1.2 -0.5 3.0 17.0 1.0 0.4 4.7 27.0 2.0 0.8 8.2
0.625
Derivace jako blackbox
V běžném světě ale typicky váhy lineární regrese neznáme a potřebujeme je nejprve spočítat. K tomu ale nejdříve potřebujeme znát jeden pojem z matematické analýzy, totiž derivaci.
Derivace je operace na funkcích a říká nám, jak se změní hodnota funkce, když velmi málo změníme jednu vstupní hodnotu (parametr). Je-li hodnota derivace v nějakém bodě kladná, pak původní funkce v daném bodě roste a roste tím strměji, čím větší je hodnota derivace. Je-li naopak záporná, pak v daném bodě klesá. A pokud je derivace nulová, pak funkce na nějakém velmi malém okolí bodu téměř nemění svoji hodnotu.
Vezměme kupříkladu funkci y = x2 a zadívejme se na její derivaci podle x. Její derivace je rovna 2x (což zatím nevíme, kde se vzalo). Pro kladná x je hodnota derivace kladná, což odpovídá tomu, že kvadratická funkce na kladných hodnotách roste. Dokonce čím větší vezmeme x, tím větší je hodnota derivace, což zase odpovídá tomu, že kvadratická funkce je s většími x čím dál strmější. Obdobně pro záporná čísla je derivace záporná, jelikož zde hodnota funkce klesá. A pro x=0 vychází derivace nulová, což zase odpovídá tomu, že kolem nuly kvadratická funkce svoji hodnotu nemění. Toto všechno ilustruje následující obrázek.
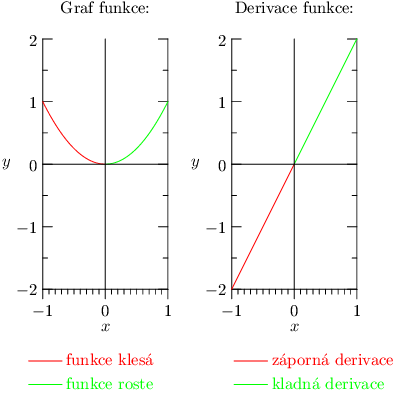
Derivujeme-li podle nějaké proměnné, ostatní parametry se vůči derivaci tváří jako konstanty (správně se těmto derivacím říká parciální derivace a vždy, když budeme zmiňovat derivace, budeme mít na mysli právě ty parciální).
Teď si můžete říct, k čemu nám to je? Když budeme mít nějakou funkci, kterou chceme minimalizovat, prostě vypočítáme derivaci a budeme hledat body, kde je derivace nulová. Proč nulová? Protože když je derivace kladná, tak zvětšení parametru zvětší i funkční hodnotu – tudíž zde určitě není lokální extrém (minimum ani maximum). To, že se jedná o minimum (nebo maximum) lokální, znamená, že se jedná o bod, který má nejmenší (či největší) hodnotu ze všech bodů v nějakém svém velmi blízkém okolí. Podobně to bude pro zápornou hodnotu derivace.
Když je hodnota derivace nulová, pak v tomto bodě může být lokální extrém, ale nemusí. Např. můžeme mít funkci, která je klesající až na nějaký úsek, v němž je konstantní. V konstantním úseku je derivace nulová, ale není zde nutně lokální extrém.
K lokálnímu extrému se váže ještě termín – globální minimum či maximum. Globální minimum znamená, že funkce z celého definičního oboru nabývá v daném bodě nejmenší hodnoty.
Globálního minima nemusí funkce nabývat jen v jednom bodě, např. funkce sinus má globální minimum hodnotu -1 a nabývá této hodnoty v nekonečně mnoha bodech. Nebo konstantní funkce y = 2: ta nabývá globálního minima na celém definičním oboru. Obdobně definujeme i globální maximum. Každé globální minimum (či maximum) je i minimem lokálním, ale naopak to neplatí – můžeme mít lokální extrém, který ale vůbec není celkově nejmenší hodnotou.
Máme-li nějaký bod s nulovou derivací, existují analytické způsoby, jak ověřit, zda se jedná o lokální minimum či nikoliv. Obzvláště ve více rozměrech však tyto metody začínají být poměrně komplikované. Co hůře, analyticky už nedokážeme poznat, zda se jedná o minimum globální. To může znít jako zásadní problém, ale prozatím se spokojíme s tím, že budeme používat samé pěkně vychované chybové funkce, o kterých lze ukázat, že mají právě jeden bod s nulovou derivací, a tím je globální minimum.
Ve skutečnosti je situace ještě o maličko zamotanější. Existují funkce, které nemají derivaci v některých bodech definovanou. A právě v těchto bodech se mohou také nacházet extrémy. S takovými funkcemi se nicméně v seriálu nesetkáme, takže pro nás bude platit, že kde je lokální či globální extrém, tam je derivace nulová.
| ∂ |
| ∂x1 |
- derivace konstanty:
c = 0, kde c je konstanta (nebo výraz ve kterém se nevyskytuje proměnná x)∂ ∂x - derivace mocniny:
xn = n ·xn-1∂ ∂x - derivace součtu je součet derivací:
(f(x) + g(x)) =∂ ∂x
+∂f ∂x ∂g ∂x - derivace složené funkce:
f(g(x)) =∂ ∂x
·∂f ∂g
. Když budeme derivovat funkci jedné proměnné, tak se zápis zjednoduší na∂g ∂x
f(g(x)) = f'(g(x)) ·g'(x), ale význam je stejný. Zderivujeme vnější funkci a vynásobíme ji derivací vnitřní funkce. Například pro funkci f(x) = (x - t)2 je derivace vnější funkce f'(y) = 2 ·y a derivace vnitřní funkce y = x - t je 1. Tedy f'(x) = (2 ·(x - t) ) ·1 .∂ ∂x
Pravidel je více, ale s těmito si vystačíme.
Optimální váhy v lineární regresi
Vraťme se k lineární regresi. Už umíme se zadanými váhami pomocí lineární regrese vytvářet predikce a už i víme, jakým způsobem můžeme pomocí MSE zjišťovat, zda váhy jsou pro nějaká data lepší nebo horší než jiné.
Co ale zatím vůbec neumíme, je pořídit si nějaké dobré váhy nebo ještě lépe ty optimální. Ba co hůř, my ani nedokážeme u zadaných vah poznat, zda jsou optimální, či nikoliv. Na to, jak hledat optimální váhy, si sice ještě budeme muset počkat do příštího dílu, ale nyní se alespoň naučíme, jak vlastně zjistit, jestli váhy optimální jsou.
Co pro takové optimální váhy musí platit? Musí to být váhy takové, že hodnota chybové funkce je nejmenší ze všech možných vah. Jinými slovy se jedná o váhy, které se nacházejí v globálním minimu. Aby se jednalo o globální (a tedy i lokální) minimum, musí být derivace podle všech proměnných rovna nule (tedy se nám nesmí stát, že by hodnota ještě někam klesala).
Sice obecně neplatí, že by nulová derivace znamenala globální minimum, ale zrovna v případě lineární regrese a MSE lze ukázat, že jediný bod s nulovou derivací vůči všem vahám je právě globální minimum.
Zbývá nám tak jediné. Zderivovat chybovou funkci podle vah a ověřit, že pro zadané hodnoty vah je vždy nulová.
Na rozdíl od predikce již nemůžeme postupovat dato po datu, protože optimalita závisí na všech datech, která máme. Speciálně již nebudeme mít jen jednu predikci p, ale několik různých predikcí p1, p2, …, pn pro jednotlivá data, stejně tak budeme mít n správných odpovědí t1, t2, …tn. Pro každé dato budeme mít opět f vstupních featur a značení xi,j nám bude říkat hodnotu j-té featury pro i-té testovací dato.
 Nyní se již můžeme vrhnout na derivaci chybové funkce.
Tato část je o něco techničtější, proto se nebojte přeskočit odvozování, pokud by
vám nepřišlo srozumitelné.
Nyní se již můžeme vrhnout na derivaci chybové funkce.
Tato část je o něco techničtější, proto se nebojte přeskočit odvozování, pokud by
vám nepřišlo srozumitelné.
Jako chybovou funkci máme MSE a chceme najít derivace podle vah w1, w2, …, wf+1:
| ||||||
| ||||||
| ⋮ |
Jelikož víme, že derivace součtu je součet derivací, tak si zkusíme zkusíme zderivovat chybovou funkci pro první predikci p1. Predikce se počítá pomocí formule p1 = x1,1 ·w1 + x1,2 ·w2 + ...+ x1,f+1 ·wf+1. Derivace chyby predikce p1 podle jednotlivých vah vyjde následovně:
| ||
| ||
| ⋮ |
Všimněte si, že derivace podle vah w1, w2, …, wf+1 jsou dost podobné, prakticky se mění jen to, jakou hodnotou x1,i vynásobíme, a tyto derivace vyjdou stejně pro všechny predikce. Tedy můžeme napsat derivaci chyby pro všechny predikce jako:
| ||||
| ||||
| ⋮ |
Zpět k původní úvaze…
Chceme, aby se výsledné derivace rovnaly nule. Po pár dalších úpravách se dostaneme k následujícím rovnicím:
| p1 ·x1,1 + …+ pn ·xn,1 = t1 ·x1,1 + …+ tn ·xn,1 |
| p1 ·x1,2 + …+ pn ·xn,2 = t1 ·x1,2 + …+ tn ·xn,2 |
| ⋮ |
Úkol 3 – Optimalita vah lineární regrese [4b]
Napište v Pythonu program, který na vstupu dostane data a váhy lineární regrese a rozhodne, jestli dané váhy jsou optimální vůči MSE metrice.
Formát
vstupu je stejný jako v druhém úkolu. Na prvním řádku vstupu dostanete dvě čísla N a F,
kde N je počet dat a F je počet featur. Na následujícím řádku naleznete F+1
desetinných čísel reprezentující váhy modelu a poslední váha reprezentuje bias.
Poté na dalších N řádcích dostanete na každém řádku F+1 desetinných
čísel. Každý z řádku odpovídá jednomu datu – prvních F hodnot na řádku jsou hodnoty
jednotlivých vstupních featur a (F+1)-ní hodnota odpovídá správné výstupní hodnotě pro dané dato.
Rozhodněte, jestli váhy jsou na daných datech optimální vůči MSE metrice.
Váhy považujeme za optimální, pokud hodnota derivace vůči žádné z vah není v absolutní hodnotě
větší než 10-6.
Pokud jsou váhy optimální, tak vypište ANO, jinak vypište NE.
3 1 1.0 4.33333333 1.0 5.0 5.0 9.0 3.0 8.0
ANO
 V typické implementaci derivací chybové funkce
a obecně všeho,
co jsme doposud dělali, se derivace a predikce nepočítají
pro jednotlivá data a jednotlivé váhy odděleně, ale
všechny najednou pomocí vektorů, matic a maticových násobení.
To proto, že tyto operace běží velmi rychle na grafických
kartách.
V typické implementaci derivací chybové funkce
a obecně všeho,
co jsme doposud dělali, se derivace a predikce nepočítají
pro jednotlivá data a jednotlivé váhy odděleně, ale
všechny najednou pomocí vektorů, matic a maticových násobení.
To proto, že tyto operace běží velmi rychle na grafických
kartách.
V seriálu matice potřebovat nebudeme, aby nebyla potřeba žádná předchozí znalost lineární algebry, ale je dobré vědět, že typicky by všechny předchozí operace byly implementovány pomocí matic.
Matice mají ještě jednu výhodu, a to tu, že se pomocí nich dají některé operace snadno zapisovat. Např. se jimi dá elegantně vyjádřit explicitní vzorec pro nalezení optimálních vah. Pokud máte odvahu, můžete si tento vzorec zkusit v následující bonusové úloze najít; pokud ne, tak si v příštím dílu ukážeme mnohem používanější a zároveň jednodušší způsob, jak optimální váhy hledat.
Pokud jste se s lineární algebrou ještě nesetkali, ale i tak by vás to zajímalo, můžete se podívat na náš seriál z minulého roku, který se lineární algebře věnuje.
Úkol 4 – Těžký bonusový úkol: Explicitní výpočet vah [0b]
Najděte maticový zápis toho, jak vypočítat všechny optimální váhy najednou. Tento úkol je zcela dobrovolný a za jeho vyřešení nedostanete žádné body.
Scikit-learn
Naprogramovat si model není nikdy na škodu, protože si většinou ujasníte, jak model funguje, a občas zjistíte, že jste si něco neuvědomili během pouhého čtení. Když už ale chcete trénovat opravdový model, tak je lepší sáhnout po nějaké knihovně, kde je daný model již implementovaný, protože knihovny jsou optimalizované na rychlost, řeší problémy s desetinnými čísly, zaokrouhlováním a spoustu dalších věcí.
V tomto seriále budeme používat jazyk Python a knihovnu scikit-learn. Knihovny na machine learning existují i pro jiné jazyky, ale v machine learningu je Python nejrozšířenější. Není se čemu divit, protože Python se používá hlavně jako rozhraní, kde zapíšete, jak má model vypadat, ale už samotný tréning modelu již neběží v Pythonu, jinak by to bylo pomalé.
Pro instalaci knihovny stačí napsat do příkazové řádky pip install
scikit-learn. Pokud nevíte jak na to, tak se podívejte na
tento návod.
Pokud budete mít problém s instalací, tak se nebojte zeptat na Discordu nebo přes email.
Nyní pojďme prozkoumávat knihovnu scikit-learn! Jedna z prvních věcí, které se hodí, je načíst si nějaká data. Scikit-learn má již nějaké datasety (kolekce/sady dat) předpřipravené, takže si je můžeme jednoduše načíst. Například dataset diabetes, který obsahuje data o pacientech s cukrovkou. V tomto datasetu máme 442 dat pacientů a každé dato má 10 hodnot (feature). Pojďme si vypsat prvních 5 dat:
import sklearn.datasets
# načtení datasetu
diabetes = sklearn.datasets.load_diabetes()
print(diabetes.data[:5])
print(diabetes.target[:5])
load_diabetes vrací objekt, který se chová jako slovník a
obsahuje data pacientů, cílové hodnoty pro predikci a pár dalších atributů.
Data o jednotlivých pacientech dostaneme z atributu data a cílové
hodnoty z atributu target. Samotná data nejsou uložená v pythoním poli,
ale v numpy poli. Numpy je matematická knihovna, která se používá pro vědecké
výpočty a najdeme tam implementované spoustu funkcí z lineární algebry (práce
s maticemi, inverze maticí, maticové rozklady, …), ze statistiky, atd.
Hlavní, co je důležité vědět, že u normálního pole v Pythonu, kde když uděláme
[:5] (slicing), tak se vytvoří nové pole. Numpy je optimalizované na
rychlost, takže se nové pole nevytvoří, ale vytvoří se jen pohled na původní
pole. Když změníme hodnotu v původním poli, změní se i v novém poli a
naopak.
Tuto vlastnost si můžeme vyzkoušet na načteném datasetu:
dato = diabetes.data[0]
dato[0] = 1
print(diabetes.data[0])
Použití numpy se budeme kvůli jednoduchosti co nejvíce vyhýbat, ale scikit-learn nám přímo vrací numpy pole, případně z numpy něco příležitostně využijeme.
Nyní máme načtená data, tak pojďme vytvořit model lineární regrese. Pro vytvoření modelu potřebujeme
naimportovat sklearn.linear_model a vytvořit model pomocí sklearn.linear_model.LinearRegression().
Konstruktor má pár parametrů, ale všechny vychozí hodnoty jsou pro nás vyhovující.
Například parametr fit_intercept říká, jestli se bude trénovat bias.
Když jsme psali výše o skrývání biasu do vstupních dat, tak toto je implementační
detail daného modelu, tedy když budete předávat vstupní data do modelu z knihovny scikit-learn,
tak není potřeba do dat přidávat jedničkovou featuru. Ale nic tím nezkazíte, když ji tam přidáte.
V daném případě by bylo dobré vypnout fit_intercept, protože poté by se v modelu
nacházely 2 biasy, což je zbytečné.
Poté model natrénujeme pomocí funkce fit(data, target), kde data jsou vstupní data
a target jsou cílové hodnoty. Nakonec máme natrénovaný model a můžeme predikovat pomocí funkce
predict(data), kde data jsou data, které chceme predikovat.
import sklearn.linear_model as lm
estimator = lm.LinearRegression()
# učíme se na všech datech kromě posledního
estimator.fit(diabetes.data[:-1],
diabetes.target[:-1])
# predikujeme poslední dato
prediction = estimator.predict(diabetes.data[-1:])
print(f"Predikce: {prediction}")
print(f"Reálná hodnota: {diabetes.target[-1:]}")
print(f"MSE: {(prediction-diabetes.target[-1:])**2}")
Úkol 5 – Prozkoumáváme scikit-learn [5b]
Scikit-learn v sobě obsahuje spoustu implementovaných modelů, užitečných funkcí a různých transformací na datech. My vás necháme prozkoumat dokumentaci scikit-learn a najít si pár užitečných funkcí.
Rozdělte diabetes dataset na trénovací a testovací množinu. Tento krok se dělá z toho důvodu, protože když trénujeme model a trénujeme ho na všech datech, tak nedokážeme otestovat, jak model funguje. Proto si část dat z trénovací množiny odebereme, aby jsme mohli na těchto datech otestovat, jak model funguje.
Následně natrénujte model lineární regrese na trénovací množině. Poté si nechte vypredikovat hodnoty pro testovací množinu a spočítejte chybovou funkci MSE. Nakonec prozkoumejte další metriky implementované v knihovně scikit-learn na měření výkonnosti modelu a zvolte si jednu vhodnou metriku pro daný typ úlohy, která vám přijde užitečná. Svůj výběr metriky krátce zdůvodněte (stačí jedna věta).
Nic nedělejte ručně, na všechno použijte knihovnu scikit-learn.
Všechny úlohy z tohoto seriálu odevzdávejte dohromady v jednom zazipovaném archivu. Všechny úlohy můžete odevzdat i v jednom souboru či Jupyter notebooku, ale tento soubor pořád musí být zazipovaný. Pokud úlohy odevzdáváte v jednom souboru, tak jednotlivé úlohy oddělte do samostatných funkcí. Termín odevzdání je 26. listopadu ve 32:00 (tedy další ráno v 8:00). Poté lze odevzdávat za snížený počet bodů až do konce ročníku.
Když budete mít jakýkoliv problém, tak se nebojte zeptat na našem Discordu či pomocí emailu. Mějte se famfárově a v příštím dílu si natrénujeme ručně lineární regresi!