První série začátečnické kategorie dvacátého šestého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 26-Z1-1: Kevin a magnety
- 26-Z1-2: Piškvorky
- 26-Z1-3: Zamilovaný dopis
- 26-Z1-4: Hroch v jezeře
- 26-Z1-5: Úkol z geometrie
- 26-Z1-6: Nezbední skřítci
26-Z1-1 Kevin a magnety (Zadání)
Magnety se přitahují tehdy, když mají naproti sobě opačné póly, a naopak se odpuzují, jsou-li umístěné stejnými póly k sobě. Částem, do kterých se magnety spojily, říkejme třeba komponenty.
Každé dva po sobě následující magnety v jedné komponentě se přitahují. Komponenta začíná buď prvním magnetem, nebo místem, kde se magnety odpuzují. Obdobně končí posledním magnetem, nebo místem, kde se magnety odpuzují, čili tam, kde začíná jiná komponenta.
Každá hranice mezi komponentami se skládá z dvojice po sobě následujících odpuzujících se magnetů. Dají se tedy jednoduše spočítat, ale z toho nedostaneme hned počet komponent. K jeho získání musíme k počtu hranic ještě přičíst jedničku: máme-li k sobě stlučených 10 prken, je mezi nimi 9 mezer.
Mohli bychom nejdříve do pole načíst orientace všech magnetů, a pak spočítat, kolik po sobě následujících dvojic se odpuzuje. Načítání a počítání odpuzujících se dvojic ale můžeme dokonce spojit do sebe: budeme si pamatovat pravou stranu posledního načteného magnetu, a když načteme další, podíváme se, jestli se s ní jeho levá strana přitahuje, nebo odpuzuje. Jestli narazíme na magnety, které jsou stejnými póly k sobě, prostě přidáme jedničku k počtu nalezených hranic mezi komponentami.
Nakonec stačí vypsat počet hranic plus jedna a dostaneme funkční řešení. Jeho časová složitost je O(N), protože načteme celý vstup a každý magnet porovnáme s jeho předchůdcem, což pro každý trvá konstantní čas. Paměti spotřebujeme jen konstantně mnoho.
26-Z1-2 Piškvorky (Zadání)
K vyřešení této úlohy nebyl potřeba žádný „trik“, stejně jsme se museli na každou pětici v programu podívat. Nejjednodušší způsob, jak s piškvorkovou hrací plochou pracovat, je použít dvourozměrné pole, „pole polí“. Do něj načteme celý vstup.
K samotnému počítání můžeme zvolit dva přístupy. První je velmi jednoduchý na napsání, ačkoli o trochu pomalejší, než ten druhý. V praxi na tom ale nezáleží, protože vzhledem k velikosti hrací plochy bude doba jejich běhu růst stejně rychle – jsou asymptoticky stejně složité.
Nejprve se podíváme na první způsob. Všimněme si, že přestože je 8 směrů pohybu z jednoho políčka, z dvou protilehlých musíme kontrolovat vždy jen jeden, jinak každou pětici započítáme dvakrát – jednou popředu a jednou pozadu.
Abychom nemuseli psát každý směr zvlášť (představte si, že kontrolujete 42-tice
místo pětic), napíšeme si na to funkci zkontroluj. Ta přijme čtyři
parametry: souřadnice startovního políčka x a y a směr zadaný jako
vx a vy – směr pohybu v obou osách s hodnotami -1/0/1.
Například pro kontrolu směrem doleva dolů z políčka [5, 6] zavoláme
funkci jako zkontroluj(5, 6, -1, 1).
Tato funkce v cyklu projde všechna políčka počínaje původním a v každém kroku provede odpovídající posun. Jakmile narazí na jiný symbol než na začátku, skončí. Pokud budou všechny stejné, zvýší odpovídající počítadlo pětic.
Tuto funkci zavoláme pro každé možné počáteční políčko pro všechny směry. Jenom
si musíme ověřit, že hledaná pětice celá leží na hrací ploše. Protože je to
snazší dělat pro konkrétní směry než obecně, nebudeme to dělat uvnitř funkce
zkontroluj, ale ještě předtím, než ji zavoláme.
Takto se ale na každé políčko podíváme 5× z každého směru (celkově tedy 20×), což je zbytečně mnohokrát. Pokud bychom chtěli tento počet snížit, můžeme zkusit druhý přístup. Pro každý sloupec hrací plochy půjdeme shora dolů a budeme počítat délku souvislého úseku. V každém kroku ji zkontrolujeme, a pokud bude větší rovna 5, víme, že přibyla další pětice. Toto provedeme i pro řádky a diagonální směry, tam to už ale začne být trochu divoké. Takto se na každé políčko podíváme pouze 4×, jednou z každého směru.
Asymptotická časová složitost obou algoritmů je lineární k velikosti vstupu, tj. O(RS).
26-Z1-3 Zamilovaný dopis (Zadání)
Kevinův problém okolo zamilovaných dopisů si nejprve zavedeme o něco formálněji, popíšeme si přirozený hladový algoritmus a na závěr dokážeme jeho správnost.
Označme si posloupnost znaků milostného dopisu jako sekvenci m0,…,mM-1. Poslopnost znaků zmoklého dopisu, o kterém chceme zjistit, zda by mohl být oním zamilovaným dopisem, si označme jako z0,…,zZ-1. Naším cílem je zjistit, zda existuje posloupnost indexů i0 < i1 < …< iZ-1 taková, že pro každé k < Z platí zk = mik.
Hladový algoritmus
Jako hladové označujeme takové algoritmy, které se ve svém rozhodování neohlíží na budoucnost, nýbrž si volí možnost, která se v danou chvíli jeví býti tou nejlepší možnou. Takový algoritmus bývá snadné vymyslet, u úloh obtížnějších než ta naše však obvykle nefunguje, či nebývá snadné jeho správnost dokázat.
Jako příklad pravděpodobně nejznámějšího hladového algoritmu jmenujme Kruskalův algoritmus pro hledání nejmenší kostry grafu. Nyní už se zabývejme naším hladovým algoritmem, který je o něco jednodušší.

Budeme postupně procházet znaky zmoklého dopisu a hledat pro každý znak jemu odpovídající znak v původním zamilovaném dopisu.
Hlavní trik, díky kterému bude algoritmus efektivní, spočine v tom, že do posloupnosti znaků zamilovaného dopisu umístíme jakousi zarážku. Ta bude oddělovat zpracované a nezpracované znaky. Pozici zarážky budeme značit jako α. Na začátku položíme α = 0.
Pozici ve zmoklém dopise bude reprezentovat proměnná k, na počátku ji nastavíme na nulu a po každém kroku algoritmu ji navýšíme o jedna. Skončíme, když k přesáhne délku zmoklého dopisu. V průběhu algoritmu budeme chtít zachovat následující invariant: Pro znaky z0,…,zk-1 jsme již našli požadované indexy i0,…,ik-1 a znaky před zarážkou jsou již „použité“, tedy ik hledáme mezi znaky zamilovaného dopisu na pozicích α,α+1,….
V jednom kroku algoritmu pak pro aktuální k hledáme index ik takto: Posunujeme zarážku doprava (navyšováním o jedna) tak dlouho, dokud znak za ní není totožný se znakem zk. Pokud takový znak existuje (nechť je na pozici p v zamilovaném dopise) nastavíme index ik roven p. Dále zvýšíme k o jedna a zarážku posuneme o ještě jednu pozici doprava (to, aby znak mp nemohl býti znovu použit).
Pokud znak nalezen není, můžeme rovnou prohlásit, že tento zmoklý dopis nemůže
odpovídat původnímu dopisu. Algoritmus tedy skončí buď zamítnutím z důvodu toho,
že se zarážkou dojel až na konec zamilovaného dopisu, či zkonstruuje celou
posloupnost indexů a pak odpoví ANO.
Jak dokážeme, že náš algoritmus funguje? Pokud odpoví ANO, pak
i zkonstruoval korektní posloupnost indexů, která dokazuje správnost odpovědi.
Pokud však odpoví NE, víme zatím pouze to, že náš algoritmus neumí
posloupnost indexů zkonstruovat. Nevíme ještě, že taková posloupnost vůbec
neexistuje.
Důkaz správnosti
Pro ověření správnosti algoritmu postačí dokázat toto tvrzení: Existuje-li posloupnost indexů j0 < …< jZ-1 taková, že pro každé k < Z platí zk = mjk, pak i náš algoritmus nějakou takovou posloupnost nalezne.
Předpokládejme pro spor, že taková posloupnost j0 < …< jZ-1 existuje,
ale náš algoritmus odpověděl NE. Označme jako k krok, ve kterém tak
algoritmus učinil. Algoritmus tedy zkonstruoval pouze posloupnost
i0,…,ik-1.
Všimněme si, že pro každé ℓ < k platí iℓ ≤ jℓ. To vyplývá z povahy našeho algoritmu – vždy volí nejmenší možný index.
Protože jk-1 < jk a ik-1 ≤ jk-1, platí ik-1 < jk. Tady tvrdíme něco strašného – algoritmus se zastavil, protože za pozicí ik-1 nenalezl znak zk, přitom však tento znak se vyskytuje na pozici jk, kde jk > ik-1, tedy leží až za ik-1.
To je spor. Popsaný případ nemůže nastat, a tedy platí naše tvrzení. Správnost algoritmu byla dokázána.
Analýza efektivity
Náš algoritmus opakuje nejvýše Z-krát hlavní cyklus. Krom posouvání zarážky proběhnou všechny operace pouze jednou v rámci jedné iterace cyklu. Zarážka se sice může posunout daleko během jedné iterace, za celý běh algoritmu se však zarážka posune o nejvýše M pozic. Proto časová složitost algoritmu je O(M+Z), kde M je délka milostného dopisu a Z délka zmoklého dopisu. Paměťová složitost je rovněž O(M+Z).
Všech K dopisů pak zvládneme otestovat s časovou složitostí O(KM+Y), kde Y je součet délek všech zmoklých dopisů. To je pro případy, kdy je délka zmoklých dopisů zhruba stejně velká jako délka milostného dopisu, optimální. Rozmyslete si, jaké řešení zvolit v případě, že místo relativně malého počtu dlouhých zmoklých dopisů, obdržíte spoustu krátkých. Kde v tomto případě algoritmus mrhá časem?
26-Z1-4 Hroch v jezeře (Zadání)
Nejdříve si přeformulujme, co po nás vlastně chce zadání. Máme určit, kolik
nejvíc znaků J obsahuje některý z ostrovů sousedící s vodní plochou, ve
které se nachází hroch. Abychom se dostali k této informaci, tak ve výpočtu
určitě musíme provést tyto kroky.
- Odhalit vodní plochu, ve které se nachází hroch.
- Identifikovat ostrovy, které s touto vodní plochou sousedí.
- Spočítat počet znaků
Jna jednotlivých ostrovech.
Na bod 1 použijeme algoritmus, kterému se říká prohledávání do šířky. Algoritmus funguje tak, že na začátku dáme do fronty (Fronta je datová struktura, do které můžeme přidávat prvky a zase je odebírat. Prvky jsou odebírány ve stejném pořadí, v jakém jsme je do fronty přidali.) startovní políčko – to, kde začíná hroch.
Pak opakujeme následující: vyndáme první políčko z fronty, podíváme se na všechna jeho sousední políčka a z nich vybereme všechna políčka vody, která jsme ještě nenavštívili, označíme je jako navštívené a přidáme je na konec fronty. Až nám políčka ve frontě dojdou, tak máme označenou celou vodní plochu, ve které se hroch nachází, a skončíme.
Řešení bodu 2 a 3 spojíme. Budeme postupně procházet všechna políčka. Když
narazíme na nějaké neoznačené políčko pevniny sousedící s označeným políčkem
vody, tak z něj opět pustíme prohledávání do šířky – tentokrát na pevninu –
a označíme tak jeden souvislý ostrov. Během odhalování ostrova budeme počítat,
na kolik znaků J jsme narazili, a budeme si pamatovat maximum, kterého
jsme dosáhli.
Celý algoritmus má časovou složitost O(SR), protože každé políčko maximálně jednou přidáme do fronty a maximálně ze čtyř různých směrů se na něj podíváme. Pak v algoritmu procházíme všechna políčka a ověřujeme, zda se nejedná o pevninu vedle označené vody – to nám také pro každé políčko zabere pouze konstantní čas.
Paměťová složitost algoritmu je rovněž O(SR). Pro každé políčko si musíme pamatovat, jakého je typu (pevnina, jídlo, voda, hroch) a jestli je či není označené.
Na závěr si ukážeme ještě alternativní možnost, jak prohledat souvislou plochu. Jedná se o algoritmus prohledávání do hloubky. Tento algoritmus se od prohledání do šířky liší pouze v tom, že políčka neukládá do fronty, ale na zásobník. (Zásobník je datová struktura, která vydává prvky v opačném pořadí, než jsme je do ní přidávali. Tedy první jde ven ten, co jako poslední přišel.)
Postup s prohledáváním do hloubky můžete vidět ve vzorovém programu. Tam jsou
dokonce všechny tři body spojeny. Prohledáváme do hloubky vodní plochu, hned jak
narazíme na ostrov, tak spustíme další prohledávání na ostrov, při kterém
spočítáme počet J, a pak zas pokračujeme v prohledávání vodní plochy.
Algoritmus s prohledáváním do hloubky má také časovou i paměťovou složitost O(RS).

26-Z1-5 Úkol z geometrie (Zadání)
Ze zadání úlohy nebylo jasné, jestli se čísla v posloupnosti mohou opakovat. Stalo se tak kvůli naší chybě, a tak jsme přijímali řešení pro obě varianty. Zamýšlena byla posloupnost bez opakovaných čísel a řešení tohoto problému jsme oceňovali až 12 body. Varianta s opakováním neměla tak pěkné řešení, bylo na ní možné aplikovat pouze jednodušší a pomalejší postup, proto jsme za taková řešení rozdělovali jen po 10 bodech.
Pomalejší řešení pro opakované body
Příklad posloupnosti: 1, 10, 5, 10, 15
Postupně čtu body posloupnosti ze vstupu a zapamatovávám si je. Řekněme, že jsem
zrovna přečetl k-tý bod – Bk. Pro každý takový bod počínaje čtvrtým
zkontroluji následující: Půlkružnice mezi bodem Bk-1 a Bk nesmí protínat
jinou půlkružnici mezi už přečtenými body. Proto pro každé ℓ mezi
0 a k-2 ověřím, jestli kružnice mezi body Bℓ a Bℓ+1 nekříží
kružnici mezi Bk-1 a Bk (všimněte si, že první číslo z posloupnosti má
index 0 a ne 1 – tak už to mají programátoři ve zvyku). To zjistíme rychle
– jeden (ale ne oba) z okrajových bodů první kružnice leží mezi dvěma body
druhé. Pokud tato podmínka platí, vypíšeme ANO a skončíme. Jinak po
takovémto zpracování všech bodů vypíšeme NE.
Tento algoritmus má pro N bodů časovou složitost O(N2), neboť pro každý z nich projde až N předchozích kružnic a pro každou z nich provede několik (konstantně mnoho) porovnání. Pamatuje si maximálně N bodů, takže má paměťovou složitost O(N).
Řešení pro posloupnost bez opakování
Tento případ se od předchozího liší několika věcmi. Například pokud se posledním bodem dostaneme pod nějakou půlkružnici, už z ní nemůžeme „ven“. Proto nám stačí vědět, pod jakou nejmenší půlkružnicí zrovna jsme, a okolní body mimo ni už nás nemusí zajímat. Podobně pokud jsou v posloupnosti body seřazené za sebou (např. 2, 3, 4, 5), žádný další bod už nesmí padnout do intervalu 2 až 5. Proto nám stačí znát jeho okraje a vnitřek nás opět nemusí zajímat. Původní algoritmus pro posloupnost bez opakování tedy sice funguje, ale díky těmto pozorováním ho můžeme výrazně zrychlit.
V následujícím algoritmu si budeme pamatovat krajní body poslední
půlkružnice (označíme levý Pℓ a pravý Pr) a až dva „zakázané“
intervaly, do kterých už žádný bod nelze umístit, jinak by došlo k překřížení
kružnic. První dva body můžeme umístit kamkoli. Pro každý další bod nejdříve
zkontrolujeme, jestli neleží v zakázaném intervalu. Pokud ano, vypíšeme ANO a skončíme.
Dále budeme rozlišovat, jestli je přidávaný bod uvnitř nebo vně poslední
kružnice. Pokud je uvnitř, přidáme k intervalům (-∞;Pℓ>
a <Pr;∞). Pokud je venku, přidáme k intervalům
<Pℓ;Pr>. Takto budeme pokračovat, dokud nepřidáme všechny body
posloupnosti. Pokud během toho nenarazíme na problém, vypíšeme NE.
Je důležité si uvědomit, že přidáním intervalu k zakázaným intervalům nám vždy opravdu vzniknou jen dva intervaly. To je dáno tím, že kružnice na sebe navazují a hraničními body intervalů jsou vždy okrajové body poslední kružnice. A jelikož jeden z hraničních bodů poslední kružnice bude vždy jedním z hraničních bodů předposlední kružnice, nikdy nám nevznikne „díra“, která by intervaly „rozpojila“ na tři nebo více.
Analýza efektivity
Díky tomu, že jsou intervaly jen dva, umíme v konstantním čase zkontrolovat, jestli bod leží v zakázaném intervalu, nebo intervaly v konstantním čase rozšířit. Přidáním každého z N bodů tedy strávíme jen konstantní čas a celková časová složitost tedy bude O(N). Pamatujeme si dva intervaly (tj. čtyři čísla, která je ohraničují) a předposlední půlkružnici (dvě čísla), takže paměťová složitost je O(1).
26-Z1-6 Nezbední skřítci (Zadání)
Poslední úloha první série KSP-Z byla trochu záludnější. Hlavním cílem bylo minimalizovat počet prohazování skřítků. Jakmile máme algoritmus, který provede nejmenší možný počet prohození, měli bychom se snažit urychlit i ostatní operace.
Zadání však neříkalo úplně přesně, jak vypadá vstup. Příklad naznačoval, že dostaneme jednotlivé skřítky očíslované podle velikosti. Pokud bychom však měli pouze jejich velikosti, tak se celá úloha trochu komplikuje.
Očíslovaní skřítci
Pokud máme skřítky očíslované, můžeme celou úlohu vyřešit poměrně elegantním způsobem. O každém skřítkovi totiž okamžitě víme, kolikátý je v pořadí, a tedy i do jaké klícky patří.
Stačí nám projít postupně všechny klícky. Pokud narazíme na skřítka, který je špatně umístěný, umístíme jej do správné klícky. Tím jsme jej však vyměnili za nějakého jiného skřítka, který nemusí patřit do aktuálně zpracovávané klece. Proto budeme tento krok opakovat, dokud nenajdeme toho správného skřítka.

Nyní by vás mohly napadat různé otázky. Podaří se nám tímto způsobem skřítky seřadit? Nemůže se algoritmus zacyklit? Provede nejmenší možný počet prohození?
Snadno si všimneme, že nikdy nepřemisťujeme skřítky, kteří jsou již ve své klícce. Pokud tedy algortimus skončí, tak předtím musel projít postupně všechny klece. Na další se přesunul pouze tehdy, když v dané kleci byl správný skřítek.
Každou výměnou umístíme vždy alespoň jednoho skřítka do své klece. Proto nemůžeme provést více než N prohození. Algoritmus tedy musí nutně skončit, a to dokonce v čase přímo úměrném počtu skřítků O(N).
Rozdělme si skřítky do jednotlivých cyklů. Cyklus pro nás bude minimální skupina skřítků, kteří jsou promícháni pouze mezi sebou. Skřítek umístěný ve správné klícce tedy sám tvoří nejmenší možný cyklus. Názornější bude obrázek:
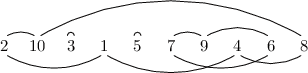
Co se s cykly stane, když prohodíme dva skřítky? Pokud byli ve stejném cyklu, tak tento cyklus rozdělíme na dva. Pokud naopak byli v různých cyklech, tak jejich prohozením cykly spojíme do jednoho.
Seřazení skřítkové tvoří N cyklů. Skřítky tedy lze seřadit nejlépe pomocí N - K prohození, kde K je počáteční počet cyklů.
Toho však dosáhne i náš algoritmus. Vždy totiž prohazuje pouze skřítky ve stejném cyklu. Provede tedy nejmenší možný počet prohození.
Známe pouze výšky skřítků
Úloha se mírně komplikuje, pokud bychom měli na vstupu pouze velikosti jednotlivých skřítků (tedy třeba čísla z velkého rozsahu, i když samotných skřítků bude málo). Nejjednodušší bude si skřítky očíslovat a převést tím úlohu na předchozí případ.
Načteme si tedy do pole jejich výšky, a ty seřadíme libovolným rychlým algoritmem v čase O(N log N). O třídicích algortimech se dočtete v tematicky zaměřené kuchařce.
Tím jsme si vytvořili pomocné pole, ve kterém binárním vyhledáváním rychle najdeme pořadí skřítka podle jeho výšky. Stačí tedy použít předchozí algoritmus s tím rozdílem, že ke skřítkovi klícku najdeme pomocí tohoto pole. Hledání nás sice trochu zbrzdí, ale celé to stihneme opět v čase O(N log N).
Důležité je ještě poznamenat, že klasickými třídicími algoritmy nemůžeme třídit přímo skřítky v klíckách, protože bychom je mezi klíckami moc často prohazovali. Použitelné by ještě trochu mohlo být třídění výběrem – SelectSort. Tento algoritmus je však pomalejší, třídí v čase O(N2).