Čtvrtá série začátečnické kategorie dvacátého devátého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 12. června 2017 v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 29-Z4-1: Šíření viru
- 29-Z4-2: Vybírání atrakcí
- 29-Z4-3: Želva v akváriu
- 29-Z4-4: Hledání součtu
- 29-Z4-5: Hanojské věže jinak
- 29-Z4-6: Tajná síť taháků
29-Z4-1 Šíření viru (8 bodů)
Kevin dostal od svého učitele informatiky domácí úkol, ve kterém si měl vybrat nějaký počítačový virus a popsat jeho chování. Při vybírání Kevina zaujal jeden zvlášť speciální kousek.
Ten se umí šířit počítačovou sítí tak, že každou minutu se nakazí každý počítač, který má alespoň polovinu svých sousedních počítačů nakaženou. Kevina napadlo, že by v rámci domácího úkolu prozkoumal, jak rychle se umí tento virus šířit v určitých počítačových sítích.
Pomozte Kevinovi zjistit, jak dlouho potrvá nakažení celé počítačové sítě, když vybere, které počítače budou nakažené zpočátku.
Tvar vstupu: Na prvním řádku jsou čísla N a K, kde N značí počet počítačů číslovaných 0 … N-1, z toho K z nich je nakažených v první minutě. Následuje řádek s K čísly nakažených počítačů. Poté následuje N řádků, každý ve tvaru p, d, s1, s2, …, sd; kde p je index počítače, d je počet jeho sousedů a si jsou jeho sousedé. Vše je odděleno mezerami.
Tvar výstupu: Na výstup vypište minutu, ve které se nakazí poslední počítač. Máte jistotu, že nikdy nenastane situace, že zůstanou nenakažené počítače.
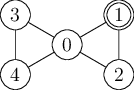
5 1 1 0 4 1 2 3 4 1 2 0 2 2 2 0 1 3 2 0 4 4 2 0 3
4
V první minutě je nakažený pouze počítač 1, ve druhé se nakazí 2, ve třetí 0 a ve čtvrté 3 a 4.
29-Z4-2 Vybírání atrakcí (10 bodů)
Skončila škola a Kevin se velmi radoval, že ze svého informatického domácího úkolu dostal nejlepší známku. Proto pozval své kamarády, že se spolu zajdou pobavit do zábavního parku.
Nezbývalo však mnoho času a navíc zábavní park byl ten den velmi vytížen. Na každé atrakci mohl tudíž ten den být jen jeden člověk. Naštěstí atrakcí bylo v tomto parku K-krát více, než byla velikost Kevinovy skupinky.
Kevin ví, že každý ze skupinky snese jinak rychlé atrakce. Někteří mají rádi rychlé a šílené jízdy, někdo jiný zase zvládne nejvýše pomaloučké houpání. Pomozte Kevinovi přidělit každému kamarádovi jeho K atrakcí tak, aby každá atrakce pro něj byla zvládnutelná a každá atrakce byla celkově použita právě jednou.
Tvar vstupu: Na prvním řádku jsou čísla N a K, kde N je počet lidí ve skupince a K · N je počet atrakcí. Na dalších N řádcích následuje dvojice čísel: nejmenší a největší rychlost atrakce, kterou daný člověk snese. Následuje řádek se seznamem rychlostí jednotlivých atrakcí.
Tvar výstupu: Na jednom řádku bude pro každou atrakci index člověka (indexujeme od nuly), kterému byla daná atrakce přidělená. Atrakce jsou v původním pořadí, jako na vstupu. Máte zaručeno, že řešení vždy existuje, nemusí však být jednoznačné.
3 3 1 9 4 6 8 12 7 5 10 3 9 4 11 6 5
0 0 2 0 2 1 2 1 1
29-Z4-3 Želva v akváriu (10 bodů)
Další den měl Kevin ve škole biologii, kde zrovna paní učitelka pustila pořad o vodních želvách. Kevin si okamžitě vzpomněl na svou vycvičenou Želvu a věděl, jaký další výcvik ji bude následovat.
Hned po škole se domluvil se Sárou, že si od Petra půjčí akvárium. Po jeho přinesení a naplnění vodou si rozmysleli, že v takovém akváriu plném vody může Želva plavat i nahoru nebo dolů. Tím ale informace, kterým směrem se Želva dívá, přestává být dostatečná na přesný popis polohy Želvy.
Když se Želva dívá na sever a otočí se nahoru o pravý úhel, už se nedívá na žádnou světovou stranu. Stejně tak, pokud se Želva dívá na sever a nakloní se, sice se stále dívá na sever, ale směr „vpravo“ již není na východ. Sára tudíž vymyslela Želvě další čtyři pokyny k otáčení: „Otoč se nahoru“, „Otoč se dolů“, „Nakloň se doleva“ a „Nakloň se doprava“.
Pro akvárium dále Kevin zavedl pomyslné souřadnice, kde [1,0,0] míří na sever, [0,0,1] směřuje na východ a [0,1,0] ukazuje nahoru. Na začátku vždy položí želvu do vody na souřadnice [0,0,0] tak, aby se dívala směrem na sever a její pravý bok míříl na východ. Poté je zajímá, na jakých souřadnicích Želva skončí. Předpokládejte, že akvárium je nekonečné do všech šesti směrů.
Když vám Kevin se Sárou postupně poví jednotlivé příkazy, dokážete říct, na jaké souřadnice Želva doplave?
Tvar vstupu: Na prvním řádku je jedno číslo, a to celkový počet příkazů.
Na dalším řádku budou samotné příkazy, kde D značí „Posuň se dopředu“
a příkazy <, >, ^, v, \ a / značí
otočení vlevo, vpravo, nahoru, dolů a naklonění vlevo a vpravo.
Tvar výstupu: Od vás budeme potřebovat na jednom řádku tři čísla oddělená mezerou, jenž značí souřadnice, kde želva skončí.
11 DD>D^D\DDvD
1 3 1
29-Z4-4 Hledání součtu (12 bodů)
Kevin a Sára si bohužel nerozmysleli, že i vycvičená suchozemská želva odmítne plavat pod vodou. Petrovi tudíž následující den po škole akvárium vrátili.
Po navracení akvária nalezli doma u Petra jednu starou deskovou hru, o které dlouho nikdo nevěděl. Jelikož měli domácí úkoly hotové, Kevin, Sára i Petr se rozhodli si hru zahrát.
Hra se skládá z kartiček s kladnými čísly. Na začátku kola se vedle sebe vyloží kartičky s čísly. Dále si každý z hráčů vylosuje své číslo.
Každý z hráčů dále hledá souvislý úsek kartiček tak, aby součet čísel na nich napsaných co nejvíce blížil jejích vylosovanému číslu. Pak vyhrává ten, kdo se svému vylosovanému číslu ve vybraném úseku přiblížil nejlépe. Je jedno, zda je tento součet menší nebo větší, než vylosované číslo. Pomozte Kevinovi tento součet najít.
Na vstupu dostanete na prvním řádku počet kartiček a vylosované číslo. Na druhém řádku následují mezerou oddělená čísla z kartiček, jak jdou vedle sebe.
Na výstup vypište tři čísla oddělená mezerou – index první a poslední karty, které jsou součástí vybraného úseku, a jejich součet. Jako obvykle, indexujeme od nuly. Pokud takových úseků existuje více, vyberte libovolný z nich.
5 30 28 44 2 21 8
2 4 31
29-Z4-5 Hanojské věže jinak (12 bodů)
Kevin pověděl své sestře Zuzce svůj zážitek se starou deskovou hrou. Zuzce se příběh líbil, hned sama začala prohledávat staré krabice s hračkami, jestli nenajde podobný poklad.
Po půl hodince našla starý dřevěný hlavolam podobný Hanojským věžím. Jde o tři tyče, přičemž na tyčích jsou rozmístěny tři disky, každý jiné velikosti. Hlavolam má základní pravidlo, a to že na disku mohou být položeny pouze menší disky. Od skutečných Hanojských věží se liší tím, že počáteční poloha není sestavená věž.
Cílem v této verzi hlavolamu je sestavit věž z disků na libovolnou tyč jejich přesouváním. Jedno přesunutí probíhá tak, že se vždy vezme jeden disk z vrchu jedné tyče a ten se přesune na vršek jiné. Při přesunu se samozřejmě nesmí porušit základní pravidlo.
Na obrázku si můžete prohlédnout možný počáteční a konečný stav hlavolamu.
Po několika málo pokusech se Zuzce podařilo hlavolam vyřešit. Přišlo jí, že to není velmi těžký hlavolam. Rozhodla se jej proto rozšířit tím, že přidala další disky. I po tomto rozšíření Zuzku pokaždé napadlo řešení. Nevěděla však, zda je nejrychlejší.
Vaším úkolem je najít způsob, jak pro dané počáteční rozmístění J disků, splňující základní pravidlo, sestavit na libovolnou tyč celou věž a přitom použít co nejméně přesunů. Součástí úkolu je i ukázat, že je váš způsob ten nejlepší.
29-Z4-6 Tajná síť taháků (14 bodů)
Nastal čas pololetních písemek a v Kevinově třídě začala vznikat tajná síť taháků. Podvádění se Kevinovi ale nelíbilo. Už jen z toho důvodu, že kdyby byl kdokoliv chycen, odskáče si to celá třída.
Kevin zjistil, že pokud kdokoliv odešle tahák jednomu kamarádovi, nemůže mu tahák přijít zpět od jiného kamaráda, tedy síť neobsahuje cykly. To znamená, že pokud by někdo ze sítě odešel, síť by se rozpadla na několik menších. A co víc, když nějaká část sítě bude moct posílat taháky mezi méně než polovinu všech původních účastníků sítě, tato část se stane příliš riskantní vzhledem k zisku a všichni účastníci skončí.
Přesvědčit spolužáka, aby ze sítě odešel, je však velmi pracné a zdlouhavé. Navíc je co se učit na písemky. Kevin tudíž ví, že má čas přesvědčit nejvýše jednoho ze svých spolužáků.
Kevin sežene popis sítě. Vaším úkolem bude vybrat spolužáka tak, aby se po jeho přesvědčení síť rozpadla na tak malé části, že celá síť skončí.