První série začátečnické kategorie třicátého prvního ročníku KSP
Celý leták v PDF.
Řešení úloh
- 31-Z1-1: Zuzka a poník
- 31-Z1-2: Ukradený jezdec
- 31-Z1-3: Průnik kvádrů
- 31-Z1-4: Piškvorky naslepo
- 31-Z1-5: Fotka zastupitelů
- 31-Z1-6: Trasa demonstrací
 31-Z1-1 Zuzka a poník (Zadání)
31-Z1-1 Zuzka a poník (Zadání)
Měli jste za úkol vypsat v sekundách délku každého kola, které Zuzka oběhla s poníkem. Délka jednoho kola je čas, který uplyne mezi dvěma stisknutími stopek: časy stisknutí v digitálním formátu dostal Váš program na vstupu. Nejjednodušším přístupem k řešení bylo si převést digitální formát na počet sekund od začátku měření: v takovémto formátu už je možné dva časy stisknutí stopek od sebe odečíst a získat čas kola.
O něco komplikovanější bylo přijít na to, jak správně (a jednoduše) převést formát stopek na počet sekund. To se může lišit v závislosti na programovacím jazyku, který používáte.
V oblíbeném Pythonu je třeba použít funkci input pro čtení řádku a
získaný řetězec rozdělit podle dvojteček zavoláním funkce split(':').
Například pokud je na vstupu řádek 00:03:13, tak zavolání input().split(':') vrátí tříprvkové pole ['00', '03', '13']. Prvky pole
jsou ale zatím řetězce, proto je třeba každý z nich převést na číslo pomocí
funkce int. Teprve potom získáme počet hodin, minut a sekund na stopkách,
s nímž můžeme pracovat dál.
V jazyce C a podobných nízkoúrovňových jazycích se s řetězci většinou nepracuje
snadno. V Céčku nás ale zachrání funkce scanf, díky které můžeme ze
vstupu přímo dostat konkrétní počty hodin, minut a sekund. Pokud si například
zadefinujeme celočíselné proměnné hod, min a sec, můžeme
voláním scanf("%d:%d:%d", &hod, &min, &sec) do nich přímo načíst
správná čísla. Všimněte si, že první parametr funkce popisuje formát řádku
(%d vyjadřuje, že na jeho místě se nachází celé číslo).
Ať už správná čísla získáme jakkoliv, získat počet sekund od začátku měření je snadné. Stačí sečíst počet sekund na stopkách, počet minut vynásobený šedesáti a počet hodin vynásobený 3 600.
Celý program pak probíhá následovně. Nejprve si načteme počet kol N. Potom provádíme N cyklů, kdy v každé iteraci načteme čas stopek, převedeme ho na počet sekund od počátku měření, odečteme od počtu sekund v předešlém cyklu a rozdíl vypíšeme. Jenom v první iteraci použijeme jako předchozí čas nulu, protože první kolo začalo na počátku měření (na stopkách byl nulový čas).
Zbývá určit časovou a paměťovou složitost celého algoritmu. Časová složitost je O(N), protože provádíme N cyklů a čas na zpracování jednoho řádku je konstantní (všechny řádky na vstupu mají omezenou délku). Paměťová složitost programu je ale konstantní – uvědomte si, že vstup čteme postupně, nemáme důvod uchovávat všechny časy kol v paměti.
Přikládáme dva zdrojové kódy v Pythonu. První program je delší a podrobnější, druhý využívá různých vlastností Pythonu ke zkrácení kódu.
 31-Z1-2 Ukradený jezdec (Zadání)
31-Z1-2 Ukradený jezdec (Zadání)
Hledání nejkratší cesty figurky na šachovnici je ve skutečnosti hledání nejkratší cesty v grafu. Pokud jste se s grafy ještě nepotkali, doporučujeme se s nimi seznámit v naší kuchařce, určitě se vám ještě někdy budou hodit.
Můžeme si představit, že každé políčko šachovnice je vrcholem a z každého vrcholu vede až T hran do jiných – každý povolený tah je jedna hrana z každého vrcholu. Pozor, tyto hrany jsou orientované, tedy pokud vede hrana z jednoho políčka do druhého, nemusí nutně vést i opačným směrem! Příkladem jsou třeba povolené tahy pěšáka, který se smí pohybovat pouze dopředu, nikdy se nevrací.
Pro řešení úlohy se hodí použít prohledávání do šířky. Algoritmus bude obsahovat frontu políček, které má zpracovat, a tu budeme pomocí smyčky procházet. Na počátku bude ve frontě pouze startovní políčko. V každé iteraci smyčky odebereme první políčko z fronty a z něj zkusíme skočit na jiné políčka pomocí každého povoleného tahu. Pokud nějaký skok, který jsme vyzkoušeli, vede na políčko, které jsme ještě nikdy nenavštívili, tak toto výsledné políčko přidáme na konec fronty.
Abychom z běhu funkce získali potřebnou cestu, vytvoříme si také pole velikosti N × N, kde budou pro každé políčko uloženy souřadnice políčka, z kterého jsme na něj skočili. Toto pole si také bude pro každé políčko pamatovat, zda jsme ho už navštívili: pokud ne, tak pro toto políčko bude v poli uložena nějaká speciální hodnota, pokud ano, tak zde budou souřadnice výchozího políčka skoku.
Pokaždé, když provedeme nějaký skok a přidáme ho do fronty, tak také zapíšeme do tohoto pole souřadnice počátečního políčka skoku na index koncového políčka skoku. Po nalezení nějaké cesty ji pomocí tohoto pole umíme rekonstruovat prostě tak, že se podíváme na výchozí místo tahu, z kterého jsme se dostali na cíl, pak na výchozí místo tohoto tahu a tak dále, dokud takto nedojdeme na počáteční místo figurky.
Toto řešení bude vracet nejkratší cesty, bude ovšem i rychlé? Pojďme se zamyslet nad obsahem fronty: na začátku bude obsahovat jediné políčko (start), na které známe nejkratší cestu délky 0. Z tohoto políčka skočíme a přidáme do fronty nějaký počet dalších políček, na která nyní známe cestu délky 1. Rychlejší cesta na ně pochopitelně existovat nebude a taky nebudou existovat žádná jiná políčka, na která by se dalo dostat cestou délky 1. Nyní zpracujeme všechna tato políčka s cestou délky 1 a vygenerujeme nová s cestou délky 2. Opět můžeme nahlédnout, že na tato políčka rychlejší cesta neexistuje, protože bychom na ně museli skočit z políčka, na které se umíme dostat pomocí cesty délky nejhůře 0 (aby byla cesta skutečně rychlejší, musí mít délku nejvýše 1), a všechny možné skoky z políček s cestou délky 0 už jsme prošli. Obecně, kdykoliv skočíme na ještě nenavštívené políčko, doskákali jsme na něj nejkratší možnou cestou délky D, protože v předchozím kroku jsme už doskákali na všechna možná políčka, na které se lze dostat nejkratší cestou délky D - 1.
Toto řešení tedy bude vracet nejkratší cestu a bude i rychlé. Každé políčko totiž navštívíme pouze jednou, tudíž zpracujeme nejhůře N × N políček.
Proč nepoužít prohledávání do hloubky?
Kromě prohledávání do šířky můžeme procházet grafem také pomocí prohledávání do hloubky, neboli užitím rekurze. Pro tuto úlohu rekurze k dostatečně rychlému řešení nepovede. Pojďme se podívat proč.
Vyjdeme z implementace z kuchařky, která navštívené vrcholy označuje a už se na ně nikdy nevrací. Tento algoritmus prostě zastavíme, jakmile narazíme na políčko cíle, a vrcholy ze zásobníku ve správném pořadí vypíšeme. Toto sice bude validní cesta, nicméně nebude to vždy cesta nejkratší, ale prostě ta první cesta, na kterou algoritmus narazí.
Řešení nyní upravíme takto: místo binární informace, jestli jsme už políčko navštívili, si budeme pamatovat pro každé políčko délku nejkratší cesty ze startu na toto políčko. V algoritmu si budeme pamatovat délku cesty na aktuální vrchol (třeba spolu s každým vrcholem v zásobníku). Vždy, když chceme zkusit do zásobníku přidat nějaký vrchol, tak se podíváme na tuto informaci a vrchol přidáme jen tehdy, pokud je současná nejkratší cesta na tento vrchol delší než cesta, kterou bychom nyní vytvořili.
Toto řešení bude správně vracet nejkratší cestu, ale bude příšerně pomalé. Má povoleno každý vrchol navštívit vícekrát, takže když bude mít obzvláště smůlu, může projít až exponenciálně mnoho (v závislosti na počtu vrcholů) různých cest, než nalezne tu nejkratší cestu do cíle. Toto rekurzivní řešení je tedy mnohem pomalejší než naše lineární řešení používající prohledávání do šířky.
 31-Z1-3 Průnik kvádrů (Zadání)
31-Z1-3 Průnik kvádrů (Zadání)
V této úloze jsme dostali za úkol spočítat obsah průniku kvádrů. Pro začátek si zjednodušme zadání a pojďme si nejprve rozmyslet, jak spočítat průnik dvou uzavřených intervalů. Označíme si proto první interval [a1, b1] a druhý [a2, b2].
Průnik těchto intervalů, pokud se protínají, bude jistě opět interval, jejž označíme [a, b]. Jaká bude hodnota a? Aby mohl průnik začít, musí taktéž začít oba základní intervaly. To znamená, že jistě a ≥ a1, a ≥ a2. Navíc tento interval začne v jednom z těchto bodů. Podobně pro konec průniku b. Ale co když se intervaly nijak neprotínají? To může nastat jen v případě, když jeden z intervalů skončí dříve, než druhý začne.
Tento způsob můžeme jednoduše rozšířit na zjištění průniku n intervalů. Pokud máme intervaly [a1, b1], [a2, b2], …, [an, bn], stejnou úvahou jistě bude pro jejich průnik platit a ≥ ai pro 1 ≤ i ≤ n. Stejně pro b. Taktéž bude fungovat i situace, když je průnik prázdný.
Dostali jsme tak způsob, jak spočítat průnik n intervalů. Nejprve spočítáme a = min(a1, a2, …, an), stejně tak b = max(b1, b2, …, bn). Pokud zjistíme, že a > b, prohlásíme průnik za prázdný.
Nyní využijme toho, že umíme spočítat průnik intervalů k tomu, abychom spočítali průnik kvádrů. Tak, jak máme kvádry zadané, jsou všechny rovnoběžné vůči sobě a jejich průnik je zase kvádr rovnoběžný s ostatními. Dále si vyzkoušejme, že „stlačením“ kvádru na přímku rovnoběžnou s jednou jeho hranou dostaneme úsečku shodnou s tou hranou. Když toto uděláme pro všechny kvádry, jejich průnikem bude úsečka – hrana průniku. Díky tomu můžeme průnik kvádru najít pro každou stranu zvlášť a výsledky zkombinovat zpět do kvádru.
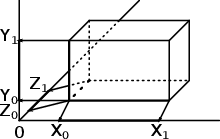
To umíme vyřešit právě přes průnik intervalů – každá hrana je určena intervalem! Po spočítání tak dostaneme trojici intervalů [X0, X1], [Y0, Y1], [Z0, Z1]. Ta nám určuje kvádr, jenž má levý spodní přední bod na souřadnicích (X0, Y0, Z0) a pravý horní zadní bod na souřadnicích (X1, Y1, Z1).
Zbývá spočítat objem tohoto kvádru. To je ale jednoduché – intervaly nám prozrazují jednotlivé délky stran, což je rozdíl koncového a počátečního bodu. Tudíž V = (X1 - X0) · (Y1 - Y0) · (Z1 - Z0). Vše zkombinujeme a dostáváme správný algoritmus, který běží v čase O(n), kde n je počet všech kvádrů.
 31-Z1-4 Piškvorky naslepo (Zadání)
31-Z1-4 Piškvorky naslepo (Zadání)
Jako první by nás mohlo napadnout udržovat si hrací plochu jako dvojrozměrné pole T, kde na každé pozici T[i][j] je znak, který se právě vyskytuje na odpovídajícím políčku v hrací ploše; pro značení prázdného políčka můžeme používat třeba znak mezery. Každý tah pak jednoduše odsimulujeme: zapíšeme na příslušnou pozici příslušný znak a pak zkontrolujeme, zda náhodou hráč, který je právě na tahu, nevyhrál.
Jak ale pole T sestrojit, když je plocha, na jaké hráči hru hrají, neomezená? Plocha sice neomezená je, ale určitě se nic nestane, když budeme uvažovat jen nejmenší obdélníkovou oblast, do které někdo zahrál. Můžeme si tedy všechny dotazy uložit někam do pole a předtím, než je zpracujeme, si nejdřív spočítat největší řádek R a sloupec S, na které jeden z hráčů zahraje, a vytvořit pole odpovídající velikosti a vyplnit ho mezerami.
Zbývá umět kontrolovat, že jeden z hráčů vyhrál. Nejjednodušší je projít celou tabulku ve všech čtyřech směrech (tj. po řádcích, sloupcích, a obou diagonálách) a průběžně si počítat, kolik stejných symbolů za sebou jsme v daném směru viděli. Řečeno kódem (pro řádky, ostatní směry by se psaly podobně):
for r in range(R):
znak = " "
pocet = 0
for s in range(S):
if T[r][s] != znak:
pocet = 0
znak = T[r][s]
pocet += 1
if pocet >= 5 and znak in "XO":
# výhra
Takové řešení má časovou složitost O(NRS), kde N je počet tahů, a paměťovou složitost O(RS), neboť pro každý tah projdeme celou tabulku.
Šetříme čas i paměť
V předchozím řešení stačilo, aby zlomyslní organizátoři přidali na vstup jeden tah na políčko [1 000 000,1 000 000], a náš program by v lepším případě spadl, v horším případě by předtím ještě zabral veškerou volnou paměť našeho počítače. Obecně se snažíme stranit algoritmů, jejichž časová a paměťová složitost závisí na hodnotě čísel na vstupu, a upřednostňujeme algoritmy, jejichž složitost závisí pouze na velikosti vstupu.
Pojďme se tedy zbavit závislosti na R a S. Brzdí nás dvě věci: na začátku vytváříme pole velikosti R × S, přestože z něj pak použijeme jen O(N) políček, a po každém tahu znovu procházíme celé pole, přestože je jasné, že pokud někdo teď vyhrál, muselo to být díky nově přikreslenému symbolu.
Místo pole T tedy použijeme nějakou „děravou“ strukturu, třeba hešovací tabulku. Ta navenek funguje podobně jako pole, ale namísto čísla ji můžeme indexovat třeba i dvojicí čísel nebo řetězcem. Pro nás je však důležitější, že obsahuje-li hešovací tabulka právě N položek, zabírá jen O(N) paměti, nezávisle na tom, jaké jsou hodnoty, kterými ji indexujeme. Za toto celé však platíme tím, že doba přístupu k jednomu prvku je O(1) pouze v průměrném případě – máme-li smůlu, může přístup trvat i O(N) času.
Pouhým nahrazením pole za hešovací tabulku si zlepšíme paměťovou složitost z O(RS) na O(N) – nesmíme už ovšem hešovací tabulku na začátku vyplňovat mezerami, namísto toho se v celém algoritmu při přístupu k nějakému políčku hešovací tabulky budeme vždy ptát, zda se v ní dané políčko vůbec nachází, a pokud ne, chápeme ho jako prázdné.
Zlepšit časovou složitost je také snadné: namísto, abychom procházeli celou tabulku [0, 0]… [R - 1, S - 1], stačí, když projdeme čtvercovou oblast [i - 4, j - 4]… [i + 4, j + 4], kde [i, j] je souřadnice políčka, na které právě někdo zahrál. Tak bude jedno zkontrolování výhry trvat čas O(92) = O(1). (Samozřejmě, kdybychom chtěli být ještě o něco rychlejší, můžeme výhru kontrolovat chytřeji a neprocházet zbytečně všechna políčka v oblasti, ale pomohli bychom si jenom o konstantu.)
Takto upravené řešení má v průměrném případě časovou složitost O(N) a paměťovou taktéž a můžeme si rozmyslet, že lépe to jít nemůže.
 31-Z1-5 Fotka zastupitelů (Zadání)
31-Z1-5 Fotka zastupitelů (Zadání)
Chceme najít v posloupnosti celých čísel nejdelší souvislý úsek, v němž se žádné číslo nevyskytuje dvakrát. Nejjednodušší řešení, které se nabízí, je projít všechny takové úseky. Pro každý možný začátek budeme zkoušet přidávat další čísla a před přidáním každého čísla vždy celý úsek projdeme a zkontrolujeme, jestli se číslo v daném úseku už nenachází. Tento algoritmus je správný, ale pomalý. Pro každý začátek provedeme až O(n2) kroků, celkem tedy O(n3).
Jde to rychleji
Všimneme si, že pokud zrovna procházíme úsek mezi i a j a zprava přidáme číslo, které už v tomto úseku je (řekněme na pozici k), žádný platný úsek, který začíná mezi i a k, nebude delší než j - i. Nemůžeme totiž přidat číslo na pozici j+1, dokud máme to samé číslo i na pozici k. Musíme tedy nejdříve vyhodit číslo na pozici k, abychom mohli získat dalšího kandidáta na nejdelší úsek.
Pořídíme si tedy dva ukazatele. Pravý ukazatel bude vždy značit pravý konec právě prohlížené posloupnosti, levý ukazatel bude značit levý konec. Nejprve budeme posouvat pravý ukazatel. Po každém posunutí zkontrolujeme, zda se nové číslo už jednou mezi levým a pravým ukazatelem nachází, nebo ještě ne. Pokud ne, můžeme posouvat pravý ukazatel dále. Pokud tam číslo již jednou je, budeme posouvat levý ukazatel, dokud na dané číslo nenarazíme a nevyhodíme ho z posloupnosti.
Tímto způsobem určitě jednou narazíme na nejdelší úsek, v němž se žádné číslo nevyskytuje dvakrát. Jistě totiž jednou pravým ukazatelem dojdeme na pravý konec hledaného úseku. Protože jsme levým ukazatelem hýbali jen v případě, že se v posloupnosti vyskytovalo nějaké číslo dvakrát, určitě nyní levý ukazatel ukazuje na začátek hledané posloupnosti. Pokud bychom se ho pokusili posunout doleva a úsek prodloužit, narazili bychom na číslo, které se v daném úseku už jednou vyskytuje (případně na začátek posloupnosti).
Tento algoritmus je o něco rychlejší než ten první. Pravý i levý ukazatel projdou celou posloupnost pouze jednou, ovšem při každém posunu pravého ukazatele procházíme celý již vybraný úsek, abychom zjistili, jestli se v něm nové číslo vyskytuje. Celkový čas tedy bude O(n2).
Trik s polem
Ukážeme, že úloha jde vyřešit i v lineárním čase. Protože máme politické strany očíslované od 0 do n - 1, můžeme si vyrobit pole délky n, do kterého si budeme ukládat, kde jsme dané číslo naposledy viděli.
Tedy pokaždé, když posuneme pravý ukazatel, podíváme se na nové číslo
a přistoupíme na pole[nové číslo]. Pokud na tomto indexu v poli nenalezneme
žádný záznam, znamená to, že v aktuálně vybrané posloupnosti mezi levým
a pravým ukazatelem toto číslo ještě není, a zapíšeme tam pozici pravého
ukazatele. Pokud však nějaký záznam nalezneme, číslo v posloupnosti už jednou
máme. Budeme tedy posouvat levý ukazatel a pokaždé, když z posloupnosti nějaké
číslo vyhodíme, vymažeme jeho záznam v poli.
Takto tedy umíme zjistit, jestli se v posloupnosti nějaké číslo nachází, v konstantním čase. Celkem nám tedy stačí O(n) času na projití celé posloupnosti a nalezení nejdelšího souvislého úseku, ve kterém se žádná čísla neopakují.
A co kdyby bylo číslování jiné?
Na závěr se můžeme zamyslet ještě nad jedním případem: co kdyby nebyly politické strany očíslovány takhle pěknými přirozenými čísly, ale nějakými ošklivými, velkými nebo zápornými?
Jedna možnost je si čísla v čase O(n log n) seřadit a přečíslovat. Algoritmus tak už nepoběží v lineárním čase, ale stále rychleji než předchozí algoritmy.
Druhá možnost je pomoct si hešovací tabulkou. V ideálním případě to bude fungovat úplně stejně jako s polem s přirozenými indexy. Občas se nám může stát, že se dvě čísla zahešují na stejnou hodnotu a budeme muset projít celé pole stejně jako u druhého algoritmu, u dobrých hešovacích funkcí se to ale neděje často a průměrná časová složitost tedy bude stále lineární.
 31-Z1-6 Trasa demonstrací (Zadání)
31-Z1-6 Trasa demonstrací (Zadání)
Jak bylo řečeno v zadání úlohy, město tvoří grafovou strukturu zvanou strom. Každá křižovatka je vrcholem a každá ulice je hranou. Pokud jste na stromy ještě nenarazili, doporučujeme přečíst si o nich v naší grafové kuchařce.
Chceme významné vrcholy stromu rozdělit do párů takovým způsobem, aby se cesta mezi vrcholy v jednom páru nepřekrývala s žádnou jinou cestou mezi vrcholy jiného páru. Okrajové křižovatky, které nejsou označené jako významné, výsledek nijak neovlivní (kdyby na ně některý průvod zašel, ocitl by se ve slepé uličce a nezbývalo by mu nic jiného, než se vrátit zpět na nějaké rozcestí).
Nejdříve nazveme nějaký libovolný vrchol stromu jeho kořenem. V tomto nově zakořeněném stromě platí, že všechny významné okrajové křižovatky jsou listy, tedy s výjimkou kořene v případě, že jsme za kořen vybrali nějakou významnou okrajovou křižovatku.
Pojďme se podívat, jak se v tomto nově zakořeněném stromě budou chovat podstromy zavěšené pod některým z jeho vrcholů. O libovolném takovém podstromě můžeme říct, že je se zbytkem stromu spojen právě jednou hranou. Z toho vyplývá, že nejvýše jedna významná křižovatka z tohoto podstromu může být spárována s jinou, která se nachází mimo tento podstrom. (Kdyby bylo s vrcholy zbytku stromu spárováno více křižovatek v tomto podstromě, znamenalo by to, že cesty mezi nimi by se nutně potkávaly právě na této hraně.)
Také z toho vyplývá, že nějaká cesta průvodu půjde přes tuto hranu právě tehdy, když má podstrom lichý počet významných křižovatek. Když jich je lichý počet, jedna z nich určitě musí být spárována s nějakou mimo tento podstrom. Pokud se v něm nachází sudý počet významných křižovatek, tak budou všechny spárované jen s křižovatkami tohoto podstromu. Kdyby tomu bylo jinak a jedna křižovatka by byla spárována s nějakou mimo tento podstrom, tak by nám v podstromě zbyla jedna nespárovaná křižovatka, a více křižovatek se zbytkem stromu spárovat nemůžeme, jak jsme již ukázali.
Nyní se podíváme na nějaký vrchol stromu a na podstromy, které mají kořen v jeho synech.
- Pokud mají všechny tyto podstromy sudý počet významných křižovatek, tak budou všechny spárovány uvnitř těchto podstromů, přes náš vrchol nepůjde žádný průvod a podstrom pod tímto vrcholem má také sudý počet významných křižovatek.
- Pokud má právě jeden z podstromů synů lichý počet významných křižovatek a ostatní sudý, tak tato přebývající křižovatka bude spárována s nějakou mimo podstrom pod tímto vrcholem a její průvod bude procházet přes tento vrchol.
- Pokud mají právě dva podstromy lichý počet významných křižovatek, tak přebývající křižovatky z obou těchto podstromů budou spárovány navzájem a cesta mezi nimi půjde přes tento vrchol.
- Pokud je lichých podstromů více než dva, tak úloha nemá řešení. Přes tento vrchol by totiž musely procházet nejméně dva průvody.
Na řešení úlohy se také dá dívat z jiného úhlu. Strom si opět někde zakořeníme. Budeme postupně obarvovat jeho hrany, které se stanou součástí cesty nějakého průvodu. Pro každý vrchol kromě kořene se musíme rozhodnout, zda hranu vedoucí do jeho otce obarvíme, nebo ne. Také pro každý vrchol musíme nejdříve počkat, než skončí obarvování v podstromě pod tímto vrcholem. Poté nám opět mohou nastat čtyři různé situace:
- Pokud není obarvená žádná hrana ze syna do tohoto vrcholu, tak hranu do otce neobarvíme
- Pokud je obarvená právě jedna, tak hranu do otce také obarvíme (pokračujeme v budování cesty z nějaké významné křižovatky)
- Pokud jsou obarvené právě dvě, tak se v tomto vrcholu právě spojily cesty mezi dvěma významnými křižovatkami a tím se spárovaly. Hranu do otce neobarvíme.
- Pokud se zde setkají více než dvě obarvené hrany, řešení neexistuje, v tomto vrcholu se nutně musejí průvody potkat.
Obarvování začneme významnými křižovatkami, nyní listy zakořeněného stromu. U těch nám nezbývá nic jiného, než hranu obarvit. Poté se přesuneme do jejich otců a provedeme obarvování, poté opět do jejich otců a tak dále.
Samotný algoritmus pro nalezení párování je stejný, ať už se na problém díváme jako na postupné dělení stromu na menší a menší podstromy nebo na obarvování hran. Jedná se o prohledávání do hloubky.
Implementace
Vytvoříme si rekurzivní funkci, která se bude spouštět na nějakém podstromě a bude vracet číslo nespárovaného listu v tomto podstromě, pokud nějaký takový list existuje. Když nějaké číslo vrátíme, je to jako bychom hranu do otce obarvili a zároveň to znamená, že tento podstrom měl lichý počet významných křižovatek. Když žádné číslo nevracíme, hranu neobarvujeme a podstrom má sudý počet významných křižovatek.
Pokud je funkce spuštěna na listě, který je významnou křižovatkou, vrátí číslo tohoto listu. Ve všech ostatních případech funkce nejdříve spustí sama sebe na všech synech aktuálního vrcholu. Pokud ze synů dostala právě dvě čísla nespárovaných listů, tak je spáruje a číslo nespárovaného vrcholu nevrací. Pokud dostala číslo jedno nebo žádné, tak tento výsledek funkce vrátí. Pokud dostala čísel více než dvě, tak řešení neexistuje.
Pro nalezení spárovaní nám stačí tuto funkci spustit na kořenu stromu, což může být zcela libovolný vrchol. Pokud jako kořen vybereme významnou okrajovou křižovatku, tak nám funkce nutně musí vrátit číslo nějakého nespárovaného vrcholu (nebo říct, že řešení neexistuje), protože podstrom pod takovým kořenem jich z pohledu naší funkce obsahuje lichý počet (samotný kořen totiž neuvažuje). Tento přebývající vrchol prostě spárujeme s kořenem.
Časová složitost tohoto řešení bude lineární vzhledem k počtu vrcholů v, protože každý vrchol navštívíme právě jednou. Paměťová bude také lineární, protože si potřebujeme pamatovat, jak vypadá náš strom, a pro stromy platí, že počet hran je roven počtu vrcholů mínus jedna; také si ale musíme pamatovat zásobník rekurze, který může mít až řádově v položek v nejhorším případě.