Druhá série začátečnické kategorie třicátého prvního ročníku KSP
Celý leták v PDF.
- Termín série: 25. února v 8:00 (praktické úlohy za třetinu bodů až do 4. března)
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 31-Z2-1: Objednávka pizzy
- 31-Z2-2: Tetris bez dozoru
- 31-Z2-3: Spousta figurek
- 31-Z2-4: Zmatematika
- 31-Z2-5: Černobílá paní
- 31-Z2-6: Dlaždice v koupelně
 31-Z2-1 Objednávka pizzy (8 bodů)
31-Z2-1 Objednávka pizzy (8 bodů)
„Jestlipak jsem se nezbláznil?“ povzdychl si Kevin, když pomáhal přenášet těžkou dřevěnou skříň, celou obrostlou pavučinami. Majitele polorozpadlého zámku za městem na podzim nenapadlo nic lepšího, než začít vyklízet harampádí v jednom z pater. Kevin se svými kamarády se přihlásili na pomoc, ale nezdálo se, že by v nějakém rozumném čase měli tohle zvládnout.
Po několika hodinách namáhavé dřiny jim majitel řekl, aby si dali pauzu, a nechal jim z města dovézt pizzu podle jejich přání. To nebylo tak snadné, protože Kevin a jeho kamarádi mají rádi různé druhy pizzy. Chtěli by ji objednávat po nakrájených osminách. V pizzerii ale umí péct jen celé pizzy, takže možná bude přivezených osminek více, než jak bylo určeno v objednávce.
Tvar vstupu: Na prvním řádku je číslo N, které určuje počet požadavků na pizzu, a na každém z dalších N řádků najdete popis požadavku. Ten se skládá z řetězce označujícího druh pizy, a počtu osminek, které bychom chtěli dovézt.
Tvar výstupu: Vypište číslo M, počet různých druhů pizz v objednávce. Na M řádcích poté vypište vždy jméno druhu a počet celých pizz, které je třeba dovézt, aby bylo dostatek osminek (ale ne zbytečně víc). Na pořadí druhů nezáleží.
5 syrova 4 hawai 5 sunkova 10 syrova 6 hawai 3
3 hawai 1 syrova 2 sunkova 2
 31-Z2-2 Tetris bez dozoru (10 bodů)
31-Z2-2 Tetris bez dozoru (10 bodů)
Na konci dne bylo jasné, že vyklízení prostorů není zdaleka u konce. Kevin a ostatní s tím ale dopředu počítali a rozhodli se, že na zámku přespí.
Kevinovi se ale nějak nedařilo usnout. Po chvíli si vzal do ruky mobil a začal hrát Tetris. Nějakou dobu se mu dařilo správně umisťovat bloky, jenže pak se polekal. Za dveřmi místnosti, kde spali, zasvítilo světlo a Kevin uslyšel nějaké kroky! Kromě jeho kamarádů, kteří spali vedle něj, teď v zámku nikdo nemohl být. Že by zloději? A co když tady straší?! Kevin probudil kamarády a vydali se na průzkum. Tetris ale zůstal nedohraný, nepozastavený, takže bloky teď padají přímo dolů, aniž by je někdo ovládal.
Pojďme se blíže podívat na skladbu tetrisových bloků. Těm se správně říká tetromina, protože každý se skládá ze čtyř kostek. Podle tvaru rozlišujeme sedm různých tetromin – až na otáčení žádné další neexistuje. Jsou pojmenovány podle písmene, které připomínají:
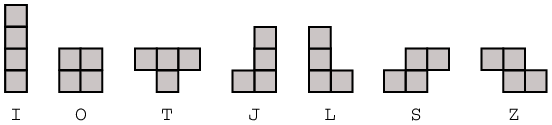
Představte si, že máme tetrisové hrací pole šířky N. Do pole nám postupně spadne K různých tetromin, pro každé víme, v jakém sloupci bude padat, nijak se ho nesnažíme posunout nebo otáčet. Jak vysoko bude sahat výsledný útvar? Pro zjednodušení nám nebudou mizet zaplněné řady kostiček a hrací pole nebude omezené výškou.
Tvar vstupu: Na prvním řádku jsou vedle sebe čísla N a K. Pak
následuje K řádků, odpovídající postupně padajícím tetrominům. Na každém
řádku je nejprve tvar – I, O, T, J, L, S
nebo Z. Následuje číslo od 0 do 3 označující otočení bloku po směru
hodinových ručiček – 0 odpovídá základnímu tvaru na předchozím obrázku, příklad
pro tvar T si můžete prohlédnout na následujícím obrázku. Posledním údajem
na řádku je pak číslo sloupce v poli, kam bude padat nejlevější kostka v bloku
(rozsahu 0 až N-1).
Jako vždy se můžete spolehnout, že vstup je korektní. Například se nestane, že bychom číslo sloupce zadali tak velké, že nějaký širší blok bude „vyčnívat“ mimo hrací pole.
Tvar výstupu: Vypište výšku výsledného útvaru.
6 4 S 0 0 Z 1 2 T 1 4 I 0 4
6

 31-Z2-3 Spousta figurek (10 bodů)
31-Z2-3 Spousta figurek (10 bodů)
Kevin s přáteli prošli celý zámek, ale nenarazili na nic, co by vysvětlovalo hluk za dveřmi. Jeden z kamarádů dokonce pojal podezření, že si z nich Kevin vystřelil. Aby noční výprava nepřišla vniveč, alespoň si z jednoho pokoje vzal starou oprýskanou šachovnici s figurkami.
Nacházela se na ní spousta černých věží a střelců a pouze jediný bílý pěšec. Kevin začal zkoumat, jestli ten pěšec je ohrožený, pokud by černý byl právě na tahu. Všechny figurky se pohybují podle standardních pravidel šachů.
Tvar vstupu: První řádek obsahuje čtyři čísla. Popořadě to je N – počet
řádků a sloupců šachovnice, C – počet černých figurek, a nakonec dvě čísla –
řádek a sloupec, kde se nachází bílý pěšák. Na dalších C řádcích se vždy
vyskytuje znak V nebo S, určující druh figurky (věž nebo střelec),
a znovu dvě čísla, řádek a sloupec s umístěním. Řádky i sloupce počítáme od
nuly.
Tvar výstupu: Zjistěte, zda některá černá figurka může vyhodit bílého
pěšáka v jediném tahu (černý je na řadě). Pokud ano, vypište pořadové číslo
černé figurky, která ho ohrožuje, v rozsahu 0 až C-1. Je-li více takových figurek, můžete si vybrat libovolnou. Pokud žádná figurka
pěšce neohrožuje, vypište NE.
Obrázek odpovídá příkladu vstupu a výstupu.
4 3 0 1 V 3 1 V 3 3 S 1 1
NE

 31-Z2-4 Zmatematika (12 bodů)
31-Z2-4 Zmatematika (12 bodů)
Víkend strávený stěhováním skončil a Kevin už zase seděl ve škole. Pořád musel myslet na noční příhodu na zámku. Že by se mu to skutečně jenom zdálo? Byl z toho tak zmatený, že když začala matematika, měl problém i s jednoduchými výpočty. Třeba s vypsáním zlomku v desetinném tvaru.
Tvar vstupu: Dostanete číslo N. Na dalších N řádcích je vždy dvojice čísel A a B, kde A je čitatel a B jmenovatel.
Tvar výstupu: Pro každou dvojici vypište na samostatný řádek zlomek
v desetinném tvaru s vyznačenou periodou.
Korektní formát má tvar xx,xxx(yy), kde yy je perioda. Ta musí
být nejkratší možná, aby byl výsledek korektní. Pokud číslo nemá periodu, tak
se část se závorkami neobjeví.
2 1 3 5251 700
0,(3) 7,50(142857)
 31-Z2-5 Černobílá paní (12 bodů)
31-Z2-5 Černobílá paní (12 bodů)
Kevin si vzpomněl, že ve městě existuje klub záhadologů. Tato skupinka lidí vždycky tvrdila, že na zámku straší. Když jim Kevin vysvětlil, co se jim stalo, vydali se na zámek s kamerami. Za pár dní zveřejnili na svých stránkách zajímavou nahrávku. Na zámku se jim podařilo natočit nějakého ducha! Protože měnil barvy mezi černou a bílou, jistě šlo o speciálního ducha, kterému se říká černobílá paní.
Místnosti zámku a chodby mezi nimi tvoří neorientovaný graf. Každá místnost má buď černé, nebo bílé energetické nabití. Černobílá paní se může po zámku přesunovat pouze po chodbách a vždy má na sobě buď černé, nebo bílé šaty. Platí, že pokud chce vstoupit do nějaké místnosti, musí mít na sobě šaty se stejnou barvou, jakou má energetické nabití místnosti. Duch si může šaty kdykoliv změnit, ale dělá to nerad, protože ho to stojí hodně energie.
Černobílá paní chce najít nejvýhodnější cestu z jedné místnosti na zámku do jiné. Nejvýhodnější znamená, že si co nejméněkrát musí po cestě změnit barvu šatů. Pokud je takto výhodných cest více, máme z nich vybrat tu nejkratší (ve které duch projde co nejméně pokojů).
Máte k dispozici graf místností na zámku, informaci o nabití místností, počáteční a cílovou místnost. Najděte nejvýhodnější cestu.
Příklad: Protože přímá cesta by znamenala tři změny šatů, musíme použít delší okliku, kde šaty měníme jen jednou. Nejvýhodnější cesta je tučně vyznačena.

 31-Z2-6 Dlaždice v koupelně (14 bodů)
31-Z2-6 Dlaždice v koupelně (14 bodů)
Zveřejněná nahrávka strašidla přinesla zámku nečekanou popularitu. Majitel otevřel jeho brány veřejnosti a brzy si vydělal dostatek peněz, aby začal stavbu rekonstruovat.
Právě teď opravuje koupelnu a přemýšlí, jak na stěny naskládá dlaždičky. Všechny budou bílé až na jednu řadu, která se bude skládat z barevných dlaždic. Chce ale, aby barvy na sebe navazovaly, tak poprosil Kevina, aby mu pomohl.
Kevin musí vedle sebe naskládat N dlaždic. K dispozici má několik druhů dlaždic, přičemž každý druh je definovaný barvou levého a pravého okraje dlaždice. Od každého druhu má Kevin k dispozici neomezeně dlaždic. Zároveň stěny nalevo a napravo od celé řady dlaždic jsou také obarvené.
Kevin musí naskládat dlaždice takovým způsobem, aby každé dvě dlaždice vedle sebe k sobě seděly barevně; zároveň levá strana první a pravá strana poslední dlaždice musí mít identickou barvu se sousední stěnou. Dlaždice není možné otáčet. Příklad správného vydlaždičkování:
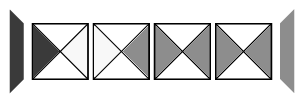
Znáte číslo N, druhy dlaždic – jejich barvy a také barvy levé a pravé stěny. Zjistěte, zda lze (nějakým způsobem) řada vydlaždičkovat, aby byla zachována pravidla.