První série začátečnické kategorie dvacátého osmého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
Řešení úloh
- 28-Z1-1: Kevinův leták
- 28-Z1-2: Sářina hra
- 28-Z1-3: Petrovy stromy
- 28-Z1-4: Zuzčina zvědavost
- 28-Z1-5: Dvě fronty na oběd
- 28-Z1-6: Osm čipů
 28-Z1-1 Kevinův leták (Zadání)
28-Z1-1 Kevinův leták (Zadání)
Nejprve si vyřešme jednodušší úlohu: jak o nějaké posloupnosti závorek poznáme, jestli je (celá) správně uzávorkovaná? Určitě musí obsahovat stejný počet levých a pravých závorek – jinak těžko mohou tvořit páry.
Ovšem to nestačí. Uvažte třeba posloupnost ())(. Ta obsahuje dvě
levé a dvě pravé závorky, ale korektním uzávorkováním určitě není.
Na třetí pozici se pokoušíme ukončit závorku „dřív, než začala“.
Jak takovou situaci poznáme? Podíváme-li se na první tři znaky naší posloupnosti, vidíme, že obsahují jednu levou závorku a dvě pravé. Obecně problém nastane, pokud existuje v posloupnosti nějaké místo takové, že v úseku od začátku po toto místo je více pravých závorek než levých. Pak alespoň jedna z těch pravých nemá před sebou žádnou levou, se kterou bychom ji mohli spárovat.
Pokud posloupnost obsahuje stejně levých a pravých závorek a nenastane problém popsaný výše, pak už si snadno rozmyslíte, že je vždy jde správně spárovat, a tedy uzávorkování je korektní.
Nyní k původní úloze. Představme si, že si chceme označit všechna
místa v posloupnosti, kde může končit korektní uzávorkování (začínající
na začátku). Třeba pro příklad ze zadání to budou následující místa
(označena hvězdičkou): (()())*()*)().
Jak je najdeme? Budeme postupně procházet posloupnost od začátku a průběžně si počítat, kolik levých a pravých závorek už jsme viděli. Pokud narazíme na místo, kde jsme napočítali víc pravých než levých, můžeme rovnou skončit. Už víme, že takové uzávorkování korektní není, a přidáním libovolných dalších závorek na konec už nemůžeme napravit chybějící závorky nalevo od aktuální pozice.
Pokud tato situace ještě nenastala a objevíme místo, před kterým je počet levých a pravých závorek stejný, označíme si jej. Podle toho, co jsme si řekli výše, uzávorkování končící na tomto místě je korektní.
Ukažme si průběh algoritmu na předchozím příkladu:
| ( | ( | ) | ( | ) | ) | ( | ) | ) | ( | ) | |
| Pozice | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Počet levých | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | - | - |
| Počet pravých | 0 | 0 | 1 | 1 | 2 | 3 | 3 | 4 | 5 | - | - |
| Rozdíl | 1 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | -1 | - | - |
| Akce | * | * | X |
Hvězdička znamená označení místa s korektním uzávorkováním
a X konec prohledávání, když žádné další uzávorkování korektní být
nemůže.
Na konci jen vypíšeme nejpravější označené místo. Všimněme si, že si nemusíme ukládat všechna označená místa, stačí si vždy pamatovat poslední dosud nalezené. Další drobné zjednodušení je místo dvou počítadel použít jen jedno, uchovávající rozdíl počtu dosud načtených levých a pravých závorek (řádek „rozdíl“ v tabulce výše). Pak označujeme, když je toto počítadlo rovné nule, a končíme, pokud klesne pod nulu.
Program (Python 3) – počítání obou druhů závorek
Program (Python 3) – stačí nám počítat jen levé
Pokud máte pocit, že jste zde dříve viděli něco jiného, nemýlíte se. Věříme, že toto řešení pro vás bude stravitelnější.
 28-Z1-2 Sářina hra (Zadání)
28-Z1-2 Sářina hra (Zadání)
Na vstupu dostaneme čísla N a M a máme zjistit, jestli po hraní M - 2 kol hry bude zastávka číslo N zakroužkovaná (kol je M - 2, protože Sára začne kroužkovat až ve druhé zastávce – v prvním kole kroužkuje zastávky dělitelné 2 a v posledním zastávky dělitelné M - 1).
Pomalé řešení
Nejjednodušší řešení by bylo vyrobit si pole zakrouzkovano s N příznaky,
kde příznak zakrouzkovano[i] značí, je-li i-tá zastávka zakroužkovaná.
V tomhle poli (M - 2)-krát nasimulujeme kolo Sářiny hry a nakonec přečteme
příznak u N-té zastávky, čímž zjistíme, jestli skončila zakroužkovaná,
nebo ne.
V Pythonu to jde napsat třeba takhle:
# N + 1, protože Python čísluje pole od nuly
zakrouzkovano = [False for _ in range(N + 1)]
for kolo in range(2, M):
# Zakroužkuj každou k-tou zastávku.
for zas in range(kolo, N + 1, kolo):
zakrouzkovano[zas] = not zakrouzkovano[zas]
print("ANO" if zakrouzkovano[N] else "NE")
Jak dlouho to poběží? Určitě aspoň Ω(N) – první kolo Sářiny hry zakroužkuje aspoň ⌊N / 2⌋ zastávek, kterým potřebujeme upravit příznaky. (Ω je příbuzná známějšího O. Když řekneme, že nějaká funkce g je v O(f(x)), znamená to, že se stoupajícím x neroste rychleji, než nějaký násobek f(x), čili „g se dá shora odhadnout f“. Ω oproti tomu značí dolní odhady: když g je v Ω(f(x)), tak g roste se stoupajícím x aspoň tak rychle, jako f.)
Kol je ale víc: první kolo potřebuje N / 2 kroků, druhé N / 3, třetí N / 4, a tak dále. Kol je celkem M a každé potřebuje nejvýš N kroků, proto nebude naše řešení potřebovat více než O(N · M) kroků. Pomalé řešení tedy poběží něco mezi Ω(N) a O(N · M). (Přesná časová složitost je O(N log M), ale na ní teď příliš nezáleží. Chcete-li zjistit, kde se vzalo N log M, podívejte se do sekce o Eratosthenově sítě v kuchařce o teorii čísel.)
Tímhle zvládneme první dva malé vstupy, ale větší nestíháme spočítat.
Druhý pokus
Zakroužkování žádné zastávky kromě N-té nás ale vlastně vůbec nezajímá,
výsledek programu na nich nezáleží. Udržování příznaků, jestli jsou
zastávky 2, … N - 1 zakroužkované, je plýtvání časem a pamětí.
Místo toho tedy projdeme kola 2, … , M - 1 a pro každé
z nich se podíváme, jestli změní zakroužkovanost N-té zastávky.
Kroužkování každé k-té zastávky změní zakroužkovanost
zastávky N právě tehdy, když je N dělitelné beze zbytku k, neboli
(v Pythonu) N % k == 0.
# Je N-tá zastávka zakroužkovaná?
zakrouzkovana = False
for kolo in range(2, M):
if N \% kolo == 0:
zakrouzkovana = not zakrouzkovana
print("ANO" if zakrouzkovano[N] else "NE")
Tohle řešení poběží v čase O(M), a to je určitě zlepšení proti prvnímu pokusu. Na plný počet bodů ale ještě nestačí.
Řešení za všechny body
Každá změna zakroužkovanosti N-té zastávky odpovídá tomu, že číslo kola k dělí N. Zastávka N je na konci zakroužkovaná, pokud počet změn zakroužkovanosti byl lichý, jinak zakroužkovaná není. Úloha se nás tedy vlastně ptá, jestli má N sudé, nebo liché množství dělitelů, kteří jsou menší než M a velcí aspoň 2.
K dalšímu zrychlení si všimneme, že dělitelé se vyskytují v párech: ke každému k1, které je dělitelem N, existuje nějaké k2 takové, že N = k1 · k2. Tohle k2 je taky dělitelem N. Dále v každém páru (k1, k2) je aspoň jedno k menší nebo rovné √N: kdyby byly obě větší, tak k1 · k2 by muselo být víc než N, ale dohodli jsme se, že to bude přesně N.
| 2 |
| 1 |
 28-Z1-3 Petrovy stromy (Zadání)
28-Z1-3 Petrovy stromy (Zadání)
Zadání sice mohlo vypadat děsivě kvůli množství proměnných, které se v něm vyskytují, ve skutečnosti je ale prosté. Podél cesty se nám pravidelně střídají stromy a nás zajímá, kolik stromů se stihne prostřídat, než uvidíme K-tý strom konkrétního druhu. V řešení budeme mluvit o topolech, ale myslíme tím prostě strom druhu J.
Připomeňme ještě označení B pro délku bloku, který se nám pravidelně opakuje.
Přímočaré řešení je uložit si celý opakující se blok do pole. Následně můžeme toto pole procházet a pamatovat si, kolik topolů a kolik stromů celkem jsme už viděli. Až potkáme K-tý topol, zahlásíme výsledek.
Takové řešení má ale složitost až O(BK), to když bude v celém bloku jeden jediný topol. Jelikož vstup má velikost O(B) a K může být mnohem větší než B, můžeme pojmout podezření, že to musí jít rychleji.
Jde, a rychlejší řešení není nijak těžké, pojďme na něj. Nejprve uvidíme nějaký počet opakujících se bloků, pak ještě část stromů z dalšího bloku a pak ten očekávaný K-tý topol.
Kolik bude bloků, které uvidíme celé? Tolik, aby se do nich spolehlivě vešlo K-1 topolů, takže (K / S) - 1, kde lomítko představuje celočíselné dělení (zbytek zahodíme) a S je počet topolů v bloku.
A kolik stromů uvidíme z dalšího bloku? Nejprve jiná otázka: kolik topolů ještě uvidíme? Tolik, kolik jich chybí do K. To většinou bude K mod S, kde „mod“ označuje zbytek po dělení. Ono slovo „většinou“ je v předochozí větě pro případ, kdy K je násobkem S, pak nám topolů chybí nikoliv 0, ale S.
Dejme tomu, že nám tedy do K chybí ještě T topolů. To ale znamená, že uvidíme tolik stromů, na kolikáté pozici je v bloku T-tý topol. Řečeno příkladem, pokud jsou třeba topoly na pozicích 2, 4 a 9 a chybí nám 2 topoly, uvidíme ještě 4 stromy, protože druhý topol je na pozici 4.
Zpočátku samozřejmě neznáme ani S, ani pozice jednotlivých topolů. Obojí ale můžeme jednoduše zjistit při načítání vstupu. Pamatujeme si, kolikátý strom právě načítáme, a taky si udržujeme informaci o počtu už načtených topolů. Když máme na vstupu topol, zvýšíme počet topolů a zároveň si uložíme jeho pozici do pole.

Na konci pak jen využijeme tyto informace k dosazení a máme výsledek. Zbývá poslední věc, a to je složitost řešení. Musíme načíst vstup, to zvládneme v O(B) (i když načítáme topol, provádíme jen konstantně mnoho operací). Závěrečné spočtení výsledku stihneme v konstantním čase, máme tedy celkovou časovou složitost O(B). Paměťová složitost je O(S), protože si musíme pamatovat pozice pro jednotlivé topoly.
 28-Z1-4 Zuzčina zvědavost (Zadání)
28-Z1-4 Zuzčina zvědavost (Zadání)
Zadání trochu krkolomně popisovalo graf, ve kterém hrany tvoří dvojice žáků, kteří se seznamovali. V tomto grafu jste měli najít počet komponent souvislosti. Pokud předchozí větě rozumíte, asi se zde nic nového nedozvíte. Jinak velmi doporučuji přečíst si naši kuchařku o grafech.

Pokud se grafových zvířátek zatím bojíte, zkusím popsat řešení v jazyce zadání. Nejprve si celé zadání načteme do paměti. Nejlépe tak, že si pro každého žáka pořídíme seznam ostatních žáků, se kterými se seznámil. Nezapomeňte, že pro každou dvojici musíte přidat dva záznamy – lidé se seznamují vzájemně.
Nyní budeme postupně procházet všechny žáky a pokud někoho ještě nemáme zařazeného v žádné třídě, vytvoříme pro něj novou (zvýšíme počítadlo tříd). Potom budeme procházet žáky, se kterými se seznámil, a u všech si označíme, že už jsme je zařadili. Tuhle operaci musíme provádět rekurzivně, tj. označit si i sousedy sousedů, sousedy sousedů sousedů a tak dále.
Prakticky si pořídíme funkci označ(Ž), která označí žáka Ž, a zavolá
sama sebe na všechny spolužáky Ž. Volání sebe sama se říká rekurze. Důležité
ale je, aby někdy přestala – pokud už je žák označený, funkce ihned skončí
a nic nedělá.
Popsanému algoritmu se říká prohledávání do hloubky, více o něm a jeho aplikacích najdete v kuchařkách.
Nejprve si pojďme uvědomit, kolik potřebujeme paměti. Pro uložení seznamů spolužáků potřebujeme N seznamů velkých nejvýše N – ale budou mít dohromady 2M prvků. Protože ale nevíme, které z čísel je větší, řekneme, že na tuto část potřebujeme O(N + M) paměti. Při dodržení podmínek ze zadání bude M < N2, ale může být i řádově menší.
Na uložení příznaků označení nám stačí N proměnných, pak už potřebujeme jen pár počítadel. Dohromady se tedy vejdeme do O(N + M) paměti.
Časová složitost vyjde stejně. Při procházení si stačí uvědomit, že po každé dvojici projdeme jen dvakrát (jednou z každé strany), a jakmile třídu uzavřeme, už se na žádného žáka z ní nepodíváme. Třída s jedním žákem je ale také třída a prohledávání, které hned skončí, musíme také započítat. Všechna prohledávání dohromady spotřebují O(N + M) času – O(N) za žaky, O(M) za dvojice.
Dodejme jen, že v některých jazycích může být volání funkce zbytečně náročná operace a může chtít příliš mnoho paměti. Potom se hodí rekurzi nahradit cyklem a žáky si ukládat do zásobníku „ručně“. Co je to zásobník a jak ho použít se dočtete ve výše zmíněné kuchařce.
Pokud místo zásobníku použijeme frontu, dostaneme prohledávání do šířky, které používá vzorové řešení v Pythonu. Jinak jsou obě možnosti ekvivalentní.
 28-Z1-5 Dvě fronty na oběd (Zadání)
28-Z1-5 Dvě fronty na oběd (Zadání)
Jsme v jídelně a máme tu dvě fronty hladových studentů seřazených podle výšky. Potřebujeme, aby se spojili v jednu frontu (také seřazenou). Jak se ale mají žáci co nejrychleji srovnat?
Někteří z vás možná poznali, že se vlastně jedná o „slévací“ funkci
merge z algoritmu MergeSort, o kterém si můžete více přečíst v naší
kuchařce o třídění. A pokud je to pro vás nové,
pojďme si ukázat, jak na to.
První žák v nové frontě musí být nejmenší ze všech. To znamená, že to bude buď první žák první fronty, nebo první žák druhé fronty. Tito dva jsou nejmenší ve své skupince (která je seřazená), tudíž určitě nikdo za nimi není menší.
Porovnáme jejich výšku a menšího pošleme do nové fronty. Možná by vás mohlo napadnout poslat do nové fronty oba, ale to udělat nemůžeme. Žák druhý v pořadí může být klidně menší než první žák z jiné fronty. Posíláme tedy vždy jen jednoho.
U jedné skupinky se tak druhý nejmenší stal nejmenším a toho opět porovnáme s nejmenším z druhé fronty. Pokud by porovnávaní žáci byli stejně vysocí, můžeme poslat libovolného, nebo dokonce oba dva (ani v jedné frontě není nikdo menší než oni).
Vždy tedy porovnáme dva aktuálně nejmenší žáky a menšího z nich pošleme na konec nové fronty. Když už bude jedna fronta prázdná, můžeme zbytek té druhé poslat do nové fronty tak, jak je (žáci jsou už seřazení).
Než vám prozradíme časovou a paměťovou složitost, je tu jeden implementační detail. Poslat žáka na konec nové fronty znamená, že informaci pouze překopírujeme. „Odebraného“ žáka nemažeme, jenom se ve frontě podíváme na dalšího. Mazat data (a tím všechna ostatní posouvat) by bylo zbytečné a neefektivní.
Každým porovnáním vybereme jednoho žáka, kterého pak pošleme na konec nové fronty. Pokud bylo v první skupince A žáků a ve druhé B, potom bude v nové frontě A + B žáků. Takže provedeme maximálně A + B - 1 porovnání, méně to bude, pokud po vyprázdnění jedné fronty zbude ve druhé více než jeden žák či pokud jsou porovnávaní žáci stejně vysocí a my je pošleme do fronty oba. Ale nás zajímá nejhorší případ, takže časová složitost bude O(A + B).
 28-Z1-6 Osm čipů (Zadání)
28-Z1-6 Osm čipů (Zadání)
Kevin si zvolí tři čísla: a, b a c. Když máme spočítat číslo k uložení
do i-tého čipu, použijeme vzorec a · xi-3 + b · xi-2 + c
· xi-1 a spočítáme, kolik vyjde po vydělení výsledku číslem N (Obecně se operaci „spočítat zbytek po dělení“ říká „modulo“
a často se dá v programovacích jazycích provést operátorem %.) Dostaneme
zadaná čísla prvních tří čipů x1, x2 a x3 a nějaké hodně velké K
a snažíme se co nejrychleji spočítat xK.
 Nejjednodušší by bylo vyrobit si pole o K prvcích, ve kterém budeme držet
hodnotu každého čipu. První tři hodnoty do něj uložíme rovnou a zbytek
dopočítáme.
Nejjednodušší by bylo vyrobit si pole o K prvcích, ve kterém budeme držet
hodnotu každého čipu. První tři hodnoty do něj uložíme rovnou a zbytek
dopočítáme.
Takové řešení potřebuje O(K) paměti na uložení pole a bude trvat čas O(K). My ale vlastně nepotřebujeme znát všech K čísel ve všech čipech: zajímá nás jenom to poslední.
A když počítáme číslo K-tého čipu, stačí nám k tomu čísla čipů (K - 1), (K - 2) a (K - 3). Podobně když počítáme číslo v čipu (K - 1), potřebujeme znát jenom čísla čipů (K - 2), (K - 3) a (K - 4).
Obecně si stačí pamatovat čísla jenom tři kroky dozadu – díky tomu naše spotřeba paměti bude konstantní, nezávisle na K. (Program navíc v praxi nejspíš i poběží rychleji: přístupy do paměti jsou rychlejší, když zapisujeme a čteme pořád do stejného místa. Zatímco první program popíše K různých míst v paměti, druhý program jenom tři.) Proměnné, ve kterých budeme držet poslední tři čísla čipů, si označíme jako x, y a z. Můžeme třeba ve for-cyklu (K - 1)-krát upravit hodnoty proměnných (x, y, z) na (y, z, (a · x + b · y + c · z) mod N).
# V x, y, z si teď budeme držet čísla
# posledních 3 čipů.
x, y, z = X1, X2, X3
for i in range(K - 1):
x, y, z = y, z, (a * x + b * y + c * z) % N
print(x)
V zadání bylo napsáno, že do K nestihnete napočítat po jedné – to znamená, že cyklus provádějící K kroků bude příliš pomalý. Ukážeme si dva způsoby, které jsou rychlejší.
Když se pozorně podíváte na zadání, všimnete si, že se čísla po nějaké době opakují. V zadání je předěl mezi opakováními zvýrazněn větší mezerou. Pokud bychom znali délku opakujícího se úseku p, můžeme skoro s jistotou říci, že K-tý čip má stejné číslo, jako (K mod p)-tý. Číslo K mod p bude určitě menší než p, takže bychom to stihnout mohli.
Nejprve učiníme pozorování: přestože zadání neslibovalo, jak velká budou x1, x2 a x3, můžeme místo nich vzít rovnou jejich zbytek po dělení N. Pokud a mod N = j, pak existuje i takové, že a = i · N + j. Potom (a · x) mod N = (i · N · x) mod N + (j · x) mod N = 0 + (j · x) mod N. Cokoliv, co násobíme N, bude N dělitelné, tedy bude mít zbytek po dělení N nula.
Další důležitá myšlenka plyne už z odstavce výše. K určení čísla i-tého čipu nám stačí čísla třech čipů dozadu. Pokud je tedy trojice čísel před čipem i stejná jako před čipem j, musí být xj stejné číslo jako xi. A díky tomu se rovnají i xi+1 s xj+1. A tak dále. Jakmile tedy najdeme stejnou trojici podruhé, nutně už musíme být v opakujícím se bloku, v periodě.
Hledání periody trochu komplikuje to, že posloupnost čísel může mít předperiodu – opakující se úsek nemusí začínat na začátku posloupnosti.
Například pro (a, b, c) = (0, 1, 1), N = 2 posloupnost může vypadat takto:
Všimněte si, že kromě prvních se tři jedničky za sebou v posloupnosti už neobjeví. Jak se tedy s předperiodou vypořádat? Pořídíme si trojrozměrné pole čísel, v každém rozměru velké N. Do něj si budeme označovat trojice po sobě jdoucích čísel čipů a číslo kroku i, ve kterém jsme danou trojici potkali. Jakmile narazíme na stejnou trojici podruhé v kroku j, našli jsme periodu dlouhou j - i s předperiodou délky i.
Když známe délku periody p a předperiody q, číslo K-tého čipu spočítáme hloupějším algoritmem výše, který spustíme pro K' = q + (K - q) mod p.
Zbývá si uvědomit, že K', tedy ani počet kroků výpočtu předperiody, nemůže přesáhnout N3 už jen díky tomu, že více různých trojic se nemůže objevit. To zároveň slouží jako důkaz, že perioda se v posloupnosti vždy objeví.
Algoritmus, který najde periodu tedy poběží v čase O(N3) a spotřebuje O(N3) paměti. Může se to zdát hodně, ale při rozumně velkém N, které slibovalo zadání, je to velké zrychlení oproti O(K). Takové řešení mohlo být za plný počet bodů.
Stále to jde ale rychleji.
 Upozorňujeme čtenáře, že následující text obsahuje zvýšené množství
matematiky. Doporučujeme!
Upozorňujeme čtenáře, že následující text obsahuje zvýšené množství
matematiky. Doporučujeme!
Podívejme se, jak se hodnoty proměnných x, y a z změní během prvního kroku (staré hodnoty označíme indexem 1 a nové indexem 2):
Rozepíšeme si tyto rovnice do tvaru, ve kterém výsledné proměnné jsou vážený součet vstupních:
| x2 | = (0 · x1 | + | 1 · y1 | + | 0 · z1) | mod N |
| y2 | = (0 · x1 | + | 0 · y1 | + | 1 · z1) | mod N |
| z2 | = (a · x1 | + | b · y1 | + | c · z1) | mod N |
Tyto lineární rovnice, které z (x1, y1, z1) počítají (x2, y2, z2), se dají taky vyjádřit jako maticové násobení těchto vektorů zleva. Pokud vám matice a vektory nejsou známé, můžete si pro naše účely představit vektory jako skupinky čísel, se kterými budeme pracovat najednou (třeba (x1, y1, z1)).
Matice jsou jenom zkratka za postup tohoto typu: z jednoho vektoru udělám jiný vektor, a složky nového vektoru jsou nějaké vážené součty složek prvního, kde váhy jsou konstanty. Právě tyhle konstanty v pořadí jako ve vzorečcích výše tvoří matici. Náš případ se dá maticově zapsat jako takovéto násobení:
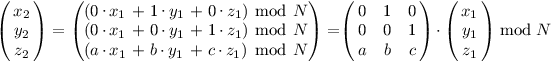
Tato matice se ještě bude hodit, tak si ji označíme:
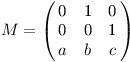
Když potom z (x2, y2, z2) počítáme (x3, y3, z3), provádíme stejné operace: x3 = y2, y3 = z2, z3 = (a · y2 + b · y2 + c · z2), neboli zapsáno maticově:
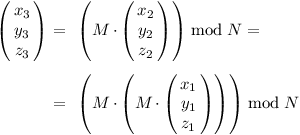
A podobně to vypadá i dál: posunutí proměnných x, y, z o jedno místo znamená jejich vynásobení zleva maticí M.
Obecně pro hodnoty x, y, z po K krocích platí:
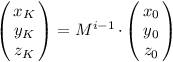
Co to ale vlastně znamená násobit matice? Násobení matic je trochu divná operace. Je vymyšlené tak, aby bylo asociativní, tedy aby pro libovolné čtvercové matice A a B a každý vektor x platilo A · (B · x) = (A · B) · x. Matice (A · B) tedy reprezentují stejnou operaci, jako nejdřív vektor „prohnat“ maticí B a pak maticí A.
Na vektorech o dvou dimenzích a maticích velkých 2 ×2 si z toho snadno můžeme odvodit, jak se musí násobit. Mějme pár matic a libovolný vektor:
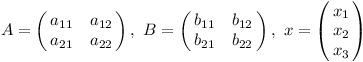
Potom:
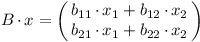
Po vynásobení A dostaneme:
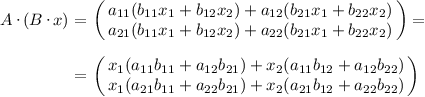
Odsud si můžeme hned přečíst, jak musí matice A · B obecně vypadat. Pro rozměr 3 je koeficientů víc, ale dají se odvodit stejným způsobem.
Teď už víme, co dělá a jak se dělá násobení matic a že je asociativní. Proto (K - 1)-násobné vynásobení x1 zleva maticí M se dá napsat jako MK-1 · x1 – nezáleží na uzávorkování.
Naše první řešení se dá popsat jako „vezmi x1, (K - 1)-krát ho zleva vynásob M a pak vrať xK“. Tohle znamená i-krát pronásobit třísložkový vektor maticí 3 ×3 (a promodulit výsledek N).
Rychlejší řešení to obejde tím, že rychle spočítá MK (modulo N) a potom vynásobí x zleva MK (a zase vymodulí). Bude nám na to stačit O(log K) násobení matic 3 ×3 a jedno násobení vektoru. Násobení matice maticí sice potřebuje více operací než násobení matice vektorem, ale obě operace trvají konstantní čas: jenom násobíme a sčítáme konstantní počet čísel na vstupu.
Díky asociativitě násobení matic se můžeme spolehnout na to, že pro libovolná g a h platí Mg+h = Mg · Mh. Číslo (K - 1) si vyjádříme jako součet mocnin dvojky (neboli ho převedeme do dvojkové soustavy) a příslušně si přeuspořádáme výpočet MK-1. Například pro K = 44 tak dostaneme M43 = M32 · M8 · M2 · M1. Takhle si rozložíme MK-1 na nejvýše ⌈ log2 i⌉ násobení matic, které jsou „dvojkové mocniny M“.
Tyhle „dvojkové mocniny M“ budeme efektivně generovat: v prvním kroku budeme držet M = M1. Jejím vynásobením samy se sebou dostaneme M2, ze které po dalším umocnění dostaneme M4, a tak dále.
V matici M' si budeme postupně stavět potřebnou matici MK-1. Počáteční hodnota M' bude maticový ekvivalent jedničky. Takové matici se říká jednotková, značí se ve třech rozměrech I3, a je to ta jediná, která se chová v násobení matic jako jednička v násobení čísel: když je T libovolná matice 3×3, potom I3 · T = T · I3 = T. Z vlastností násobení se dá uhodnout, jak I3 vypadá. Má nuly všude kromě diagonály, kde má jedničky:
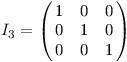
Budeme se posouvat v binárním zápisu čísla (K - 1) zprava doleva. Na začátku kroku číslo i budeme mít uloženou prozatímní matici M' a matici M2i. Podíváme se na i-té číslo zprava v binárním zápisu, a jestli tam uvidíme jedničku, přenásobíme M' maticí M2i.
Ať vidíme jedničku nebo nulu, umocníme M2i na druhou, čímž si spočítáme pro další krok M2i+1. Po každém kroku taky vymodulíme obsah M2i+1 i M' číslem N. Tohle modulení musíme provádět, abychom zajistili, že všechny použité proměnné budou omezeně velké, konkrétně mezi 0 a N-1. Bez modulení by totiž mohly růst hodně rychle a ukládat velká čísla nestojí konstantně mnoho paměti.
Z výsledku nás zajímá jenom xi mod N a to vyjde stejně ať počítáme přesně, nebo modulo N. (To platí, protože (a + b) mod N = [(a mod N) + (b mod N)] mod N a (a · b) mod N = [(a mod N) · (b mod N)] mod N. xi vznikne z (x0, y0, z0) jenom jejich posloupností, proto můžeme všechny mezivýsledky včetně matic ukládat modulo N.)
Na konci bude M' součin těch mocnin M, které odpovídají vahám jedniček v binárním zápisu (K - 1), tedy bude M' přesně rovna MK. Za každou číslici v binárním zápisu (K - 1) provedeme jedno nebo dvě násobení matic, což trvá konstantní čas, a protože číslic je logaritmicky mnoho, trvá náš algoritmus jenom O(log K). Dá se navíc naimplementovat tak, že mu stačí jenom konstantní množství paměti.