Druhá série začátečnické kategorie dvacátého osmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 28-Z2-1: Před muzeem
- 28-Z2-2: Práce pro Sáru
- 28-Z2-3: Byli jsme tři
- 28-Z2-4: Rozsypaná turbína
- 28-Z2-5: Příkop u Tří soutěsek
- 28-Z2-6: Kalamita
 28-Z2-1 Před muzeem (Zadání)
28-Z2-1 Před muzeem (Zadání)
U úloh tohoto typu, kde je na první pohled spousta různých správných výsledků, se často vyplatí hledat nějaké konkrétní, třeba v nějakém smyslu nejmenší nebo první. Lépe pak vyplyne, že pokud jsme řešení nenašli, tak neexistuje.
Ukážeme si jednoduché řešení, které nám nezabere více času než vůbec přečíst vstup. Pořídíme si dvě ukazovátka a pojmenujeme si je jehla a seno. Jehla bude ukazovat na prvního žáka v hledané skupince (první znak na druhém řádku) a seno na prvního žáka v řadě (první znak v řádku třetím).
Nyní budeme hledat jehlu v kupce sena. První žák, kterého vybereme do skupinky, musí začínat písmenem, které nám určuje jehla. Pokud do skupinky dáme prvního takového, určitě nic nezkazíme!
Budeme tedy posouvat ukazovátko seno, a jakmile se bude znak pod jehlou a senem shodovat, vypíšeme pozici sena na výstup. Pak posuneme jehlu doprava a opakujeme úvahu. Další vybraný žák může být bez újmy na obecnosti ten první, na kterého narazíme. Jakmile vybereme všechny žáky ze skupinky (dojedeme jehlou na konec řádky), končíme.
Pokud bychom vyjeli senem za konec třetího řádku, víme jistě, že žádná taková skupinka mezi žáky není. To ale zadání zakazovalo a vstupní data tento případ neobsahovala.
Všimněte si, že ukazovátka posouváme jen doprava a přes každé písmenko přejede ukazovátko jen jednou. Algoritmus běží v čase lineárním se součtem čísel na prvním řádku, tedy s velikostí vstupu.
Program je opravdu jednoduchý, proto si v tom Céčkovém dovolíme trochu magie. Zkuste si rozmyslet, co se tam děje.
 28-Z2-2 Práce pro Sáru (Zadání)
28-Z2-2 Práce pro Sáru (Zadání)
Ještě než si ukážeme samotné správné řešení, zodpovíme otázku, která vám jistě vrtá hlavou: kde se tato jednoduchá hříčka s násobením a dělením čísel vlastně vzala? Ve skutečnosti je to matematický problém známý jako Collatzova domněnka (Collatz conjecture).
Ta říká, že pokud vezmeme jakékoliv přirozené číslo a stále dokola na něj aplikujeme pravidla ze zadání (pokud je sudé, vydělíme jej dvěma; pokud je liché, vynásobíme jej třemi a přičteme jedničku), tak se vždy nakonec dostaneme do jedničky.
Problém byl poprvé formulován v roce 1937 matematikem Lotharem Collatzem a doposud zůstává nevyřešený – tedy nikdo ještě nenašel důkaz, že domněnka platí pro jakékoliv číslo.
Počítačovou simulací se ověřila správnost pro všechny hodnoty menší než cca 260 (v naší úloze jste dostávali daleko menší). To však neznamená, že se protipříklad, tedy nějaké číslo, které do jedničky nedojde, nemůže vyskytovat mezi ještě většími hodnotami.
A jak tedy vyřešit zadanou úlohu? Přímočarým řešením je na každé číslo z intervalu aplikovat pravidla a přitom počítat, kolik kroků potřebujeme pro dosažení jedničky. Následně vypíšeme číslo, které má tento počet nejvyšší. Takový postup stačil na vyřešení menších testovacích vstupů.
Pokud máme zájem o rychlejší řešení, musíme uvažovat, zda nepočítáme něco víckrát, než je nutné. Při počítání kroků se často dostaneme do čísla, v němž jsme se předtím již vyskytli, a postup zbytečně opakujeme. Například pro interval 4… 8 je počet kroků pro osmičku roven počtu kroků pro čtyřku plus jedna – toho ale při počítání osmičky využít nemůžeme, jelikož si počty nikde nepamatujeme.
Optimálním řešením je si vytvořit pole, indexované všemi možnými hodnotami, do kterých se při počítání kroků můžeme dostat. Typicky budeme vycházet z maximálního možného čísla na vstupu.
Hodnoty, které nám vyjdou při počítání, ale mohou být ještě větší, takže musíme udělat rozumný odhad. Na indexu I bude zapsán počet kroků, než se z čísla I dostaneme do jedničky, nebo -1, pokud jej zatím neznáme. Na začátku budou všechny hodnoty v poli nastavené na -1.
Pro každé číslo z intervalu pak aplikujeme pravidla jako předtím, ale pamatujeme si hodnoty, přes které jsme prošli. Jakmile narazíme na číslo, jehož počet kroků již známe (a je tedy uložený v poli), vrátíme se přes zapamatované hodnoty zpět až do původního čísla a přitom každému nastavíme správný počet kroků. Zbytek probíhá stejně jako u původního řešení.
Protože si nejsme jisti, že algoritmus skončí, nebudeme ani obecně určovat časovou složitost.
 28-Z2-3 Byli jsme tři (Zadání)
28-Z2-3 Byli jsme tři (Zadání)
Jak můžeme mezi všemi lidmi ve škole najít ty trojice, které tvoří dobří přátelé? Připomeňme ještě, co dostaneme na vstupu: počet lidí N, počet dvojic lidí, kteří spolu kamarádí K, a následně K dvojic typu (a, b) říkajících, že osoba a a b jsou kamarádi.
Pokud jste už někdy slyšeli o teorii grafů, asi pro vás nebylo těžké si úlohu představit a pochopit správně zadání. Pokud jste o grafech ještě neslyšeli, velmi doporučujeme přečíst si základní kuchařku. Pro pochopení tohoto textu sice není nezbytná, ale může vám pomoci při řešení dalších podobných úloh.
Ale zpět k úloze. Jak ji řešit? Může nás napadnout přímočaré řešení. Vyzkoušíme všechny trojice lidí a ověříme, zda se každá ze tří dvojic zná. Přímou implementací dostaneme sice funkční, ale velmi pomalé řešení. Vyzkoušení všech možných trojic zařídíme snadno pomocí tří vnořených cyklů. Všech možných trojic je řádově O(N3). A pro každou z nich projdeme vždy celý vstup, abychom mezi všemi přátelstvími našli tři dvojice lidí (a, b), (b, c) a (c, a).
Musíme si dát pozor, kolikrát trojici započítáme. Na každou totiž narazíme
postupně šestkrát, například jako na trojice 012, 021, 102, 120, 201,
210. Tento problém můžeme vyřešit dvěma způsoby: buď výsledek před vypsáním
vydělíme šesti, nebo trojici započítáme pouze v případě, že čísla jednotlivých
lidí budou v rostoucím pořadí. Na to nesmíme zapomenout ani v následujících
řešeních, v popisu to však již znovu rozebírat nebudeme.
Celková časová složitost popsaného algoritmu je O(N3K). Za takovéto řešení ale moc bodů získat nešlo.
Zrychlujeme
Čím trávíme drahocenný čas zbytečně? Hledáním. Řešení výše pořád dokola hledá v celém seznamu přátelství jednotlivé dvojice. Co kdybychom o každé dvojici dokázali říct okamžitě, zda se dotyční přátelí, či nikoli? Rázem bychom dostali řešení s časovou složitostí O(N3).
Jak to tedy zařídit? Pořídíme si tabulku N×N – dvourozměrné pole, kde na pozici (i, j) bude jednička, pokud jsou lidé i a j přátelé, v opačném případě nechápe políčko nulové. V řeči grafů bychom této tabulce říkali matice sousednosti.
Asi vám nemusíme složitě popisovat, jak takovou tabulku získat. Na začátku si jednoduše přečteme řádek po řádku celý vstup a vždy si do matice sousednosti zapíšeme na odpovídající pozice jedničku. Jen nezapomeňte, že přátelství jsou vzájemná, takže si chceme zapsat jedničku jak na pozici (i, j), tak zároveň na (j, i).
Sestavení tabulky nám zabere čas O(N2 + K). Pokud totiž chceme nějakou paměť používat, musíme si ji nejprve připravit. A to zabere řádově tolik času, kolik paměti chceme. (Toto se nemusí vždy projevit, protože paměť za nás může připravit operační systém. Často to dokonce udělá těsně před samotným zápisem do paměti.) I tak je však příprava rychlejší, než samotné zkoušení všech trojúhelníků. Časová složitost je tedy O(N3) a paměťová O(N2).
| N ·(N - 1) ·(N - 2) |
| 6 |
Máme tedy vyhráno? Ještě ne. V zadání byla společná horní hranice pro počet lidí i přátelství: N, K ≤ 105. Rozhodně tedy nemůže nastat případ, kdy N = 105 a každý zná každého, protože pak by všech přátelství bylo téměř 1010. Zajímáme se zkrátka o případy, ve kterých je řádově stejně lidí jako dvojic přátel. Můžeme tedy hovořit o takzvaném řídkém grafu – grafu, který neobsahuje mnoho hran.
Husté řešení pro řídké grafy
Z čeho se taková trojice přátel skládá? Ze tří lidí a tří přátelství. Zatím jsme zkoušeli brát postupně všechny trojice lidí a k nim dohledávali přátelství. Mohli bychom to také celé otočit. Vezmeme-li jedno konkrétní přátelství (řádek vstupu, čili jednu informaci, kterou si Sára zapsala), určuje nám jednoznačně hned dvě konkrétní osoby a a b. K nim už stačí jen vzít všechny přátele b a zjistit, zda jsou také přáteli a; pokud ano, našli jsme trojici.
Technicky zlepšení dosáhneme i jen díky tomu, že budeme existenci přátelství kontrolovat průběžně a ne až pro celou trojici dohromady.
Tím dostaneme řešení s celkovou časovou složitostí O(K·N), pro každý vztah vyzkoušíme N lidí na doplnění trojice. Abychom omezili i paměťovou náročnost, musíme se ještě zbavit matice sousednosti (a nerozbít si u toho složitost časovou).
Pro každého si budeme pamatovat seznam lidí, se kterými se přátelí. Pořídíme si
k tomu N-prvkové pole (pojmenujme si je třeba P) obsahující spojové
seznamy. Následně budeme pole procházet – tím získáme prvního z trojice, a.
Procházením seznamu přátel a budeme dostávat b, takto tedy iterujeme přes
všechna přátelství.
Nyní stačí projít všechny přátele b a zkontrolovat u nich pouze to, že se také přátelí s a. Ke kontrole přátelství s a jsme dříve používali právě matici sousednosti. Tu teď sice k dispozici nemáme, ale nic nám nebrání si vždy vytvořit jeden její řádek – ten s kamarády a.
Celé řešení proto bude vypadat takto: projdeme postupně naše pole P
a pro každého člověka uděláme následující tři kroky. Nejprve vytvoříme jemu
odpovídající řádek z matice sousednosti (projitím jeho seznamu přátel).
V druhém kroku budeme trojúhelníky počítat, postupně pro každého z již projitého seznamu kamarádů a. A to tak, že ověříme, kteří přátelé b jsou i přáteli a. Za každého společného přičteme jedničku k celkovému počítadlu trojic.
Na závěr projdeme seznam ještě jednou a řádek matice po sobě zase uklidíme (vynulujeme místa s jedničkou), tím si ho připravíme pro dalšího člověka.
Paměťová složitost je tedy O(K + N) a časová slíbených O(K·N). A co říci závěrem? Nezapomeňte výsledek vydělit šesti.
 28-Z2-4 Rozsypaná turbína (Zadání)
28-Z2-4 Rozsypaná turbína (Zadání)
Jako první si všimneme jedné zajímavé vlastnosti. Každé písmeno se objeví na horní straně lopatky právě tolikrát, kolikrát se objeví na spodní straně.
Proč tohle platí? Představme si třeba, že v poskládané turbíně nebudeme koukat na lopatky samotné, ale na jejich spojení – to vždy obsahuje stejné písmenko, jednou nahoře, jednou dole.
Zkusme teď lopatky poskládat. Jako první nás asi napadne nejprve vzít náhodnou lopatku, pod ní připojit libovolnou z těch, které pod ní připojit smíme, a tak dále.
Jestliže už mezi nezapojenými lopatkami není žádná, kterou bychom mohli přidat, musí být možné spojit poslední a první lopatku. To plyne právě z toho, že všechna písmenka se vyskytují stejněkrát nahoře i dole. Pokud má poslední lopatka dole písmeno A a žádná nezapojená lopatka nemá A nahoře, někde nám jedno volné „horní A“ chybí. Na spoji zapojených lopatek to být nemůže, tam jsou písmenka „obsazená“, musí to tedy být na první lopatce.
Skvělé, sestavili jsme turbínu. Ta ale nemusí být stejně velká jako ta původní, klidně nám mohly zbýt nepoužité lopatky. Co s nimi uděláme? Někam je vložíme.
Když se budeme postupně dívat na jednotlivé lopatky hotové turbíny, dříve nebo později potkáme takovou, na kterou bychom (kdyby nebyla obsazená) mohli napojit nějakou z nezapojených lopatek.
Turbínu tedy rozpojíme. Označme si rozpojené lopatky třeba 1 a 2. Teď k lopatce 1 připojíme nezapojenou lopatku a k ní budeme opět přikládat libovolnou lopatku z těch, které přidat smíme (jsou nezapojené a mají stejné písmeno). Podobným argumentem jako prve dojdeme k tomu, že až nebudeme mít co připojit, musí být možné poslední přidanou lopatku spojit s lopatkou 2.
Stejně můžeme pokračovat a zapojit další zbývající lopatky. Jen pozor, při zkoumání lopatek v turbíně musíme pokračovat z lopatky 1, nikoliv 2, může se nám totiž stát něco podobného jako na obrázku:
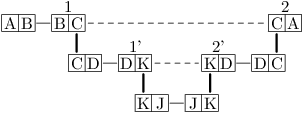
Na začátku máme nalezený cyklus AB BC CA. Do něj se nám podaří vložit
lopatky CD DK KD DC, takže dostáváme AB BC CD DK KD DC CA. Ve
vkládání pokračujeme od lopatky 1 (BC). Přímo k ní už nic dalšího
nenajdeme, tak pokračujeme lopatkou CD. Turbínu ovšem rozpojíme až za
DK.
Rozmysleme si, že takto můžeme postupně přidat opravdu všechny lopatky. Kdyby to možné nebylo, musí nám zůstat alespoň jedna lopatka označená písmenkem, které se vyskytuje v hotové turbíně. Jinak by vůbec nebylo možné všechny lopatky spojit, ale my víme, že to jít musí (předtím spojené byly).
Jenže my lopatku v hotové turbíně neopustíme, dokud na ni můžeme něco napojit, tedy bychom naši zbylou lopatku bývali zapojili. Takže nám žádná taková lopatka zbýt nemůže.
Dobře, teď musíme takový postup efektivně naimplementovat. K implementaci můžeme dojít dvěma úvahami, buď do nich zahrneme klasické grafy, nebo ne.
Úvahy bez grafů
 Hotovou turbínu budeme reprezentovat jako obousměrný spojový seznam,
abychom do ní uměli rychle vkládat nové lopatky.
Hotovou turbínu budeme reprezentovat jako obousměrný spojový seznam,
abychom do ní uměli rychle vkládat nové lopatky.
Horší je to s nezapojenými lopatkami, ty si potřebujeme pamatovat a zároveň v nich chceme umět rychle najít libovolnou vhodnou lopatku, tedy lopatku označenou konkrétním písmenem.
Tady trochu zneužijeme, že písmenek je málo. (Podotkněme, že kdyby jich málo nebylo, můžeme udělat něco podobného, ale bude to technicky komplikovanější.) Pořídíme si pole indexované písmenky (resp. třeba jejich pořadím v abecedě). Prvky tohoto pole budou spojové seznamy lopatek, které mají na horní straně dané písmenko.
Když budeme potřebovat lopatku označenou daným písmenkem, jednoduše vezmeme první z příslušného spojového seznamu.
Jakou bude mít náš algoritmus složitost? Začněme od přidání lopatky do hotového kusu turbíny. To je konstantní, O(1), protože smazat první prvek ze spojového seznamu i vložit za konkrétní prvek zvládneme v konstantním čase.
Malá zrada přichází, když si rozmyslíme složitost projití celé turbíny. Mohlo by se zdát, že ke každé lopatce můžeme přinejhorším připojit všechny lopatky, tedy při N lopatkách by byla složitost O(N2). Ale během celého algoritmu můžeme přidat jen N lopatek, takže celé napojování trvá O(N).
Načtení vstupu i výpis výstupu nám trvá lineárně, celý algoritmus má tedy časovou složitost O(N). Lineární je i paměťová složitost, celou dobu máme někde uložené informace o N lopatkách (byť se lopatky přesouvají mezi jednotlivými spojovými seznamy).
Úvahy s grafy
Jestli se grafů nebojíme, můžeme úlohu jednoduše převést na grafový problém. Pokud jste někdy slyšeli o hledání eulerovského tahu, měl by vám ho popsaný postup nápadně připomínat. V opačném případě vřele doporučujeme přečíst si kuchařku o procházkách v grafu.
Jak ale převést lopatky na graf? Vcelku jednoduše, z písmenek uděláme vrcholy, z lopatek pak hrany (za každou lopatku povedeme hranu z písmene na její horní straně do písmene na dolní straně). Jenom pozor, že mezi dvěma vrcholy může vést více hran (můžeme mít dvě stejné lopatky). Grafu s takto násobnými hranami se říká multigraf.
Použití všech hran teď odpovídá použití všech lopatek. Průchod přes vrchol pak zajišťuje, že lopatky na sebe budou správně napojené, tj. že první lopatka končí stejným písmenem, jakým začíná druhá lopatka.
Tím, že se písmeno musí vždy vyskytovat stejněkrát na horní i dolní straně, budou mít všechny vrcholy sudý stupeň, eulerovský tah tedy existuje. Stačí nám tak pustit na grafu klasický algoritmus.
Zbývá nám určit složitost. Jak slibuje kuchařka, algoritmus na hledání eulerovského tahu je lineární v počtu vrcholů a hran. Protože písmenek máme „málo“, můžeme jejich počet prohlásit za konstantní, do složitosti se nám tedy promítne jen počet hran, což je vlastně počet lopatek.
Pro úplnost dodejme, že vytvoření grafu zvládneme také v lineárním čase – pro každou lopatku v konstantním čase přidáme do grafu hranu (tj. prvek do spojového seznamu sousedů příslušného písmena). Celý algoritmus bude mít tedy pro N lopatek složitost O(N).
Poznámka na okraj
Snadno si můžeme rozmyslet, že obě úvahy vedou na velmi podobný program, liší se opravdu jen způsob uvažování a pojmy, které používáme. Kouzlo informatiky je, že v takovýchto případech si každý může vybrat ten přístup, který mu vyhovuje, a přesto máme všichni stejně dobré řešení.
 28-Z2-5 Příkop u Tří soutěsek (Zadání)
28-Z2-5 Příkop u Tří soutěsek (Zadání)
Způsobů, jak vyřešit tuto úlohu, bylo více. My zde ukážeme několik variant řešení, které jsou lineární s délkou příkopu. Předpokládáme, že vstupem je řada čísel, kde každé vyjadřuje výšku příkopu na jednom decimetru délky.
Jedno z možných řešení mohlo vypadat následovně – pro každý úsek (každý decimetr) zjistíme, jakou největší výšku má příkop od něj nalevo a napravo. Voda se na dané části může udržet do menší z nich, protože jinak odteče.
Spočítat to můžeme tak, že projdeme příkop zleva i zprava a při jednom průchodu si pro každou část zapisujeme doposud největší výšku. Nakonec si z hodnot na stejných pozicích zapamatujeme tu nižší.
Podívejme se na příklad:
| Vstup: | 1, 3, 2, 5, 4, 1, 3, 2 |
| Maxima průchodu zleva: | 1, 3, 3, 5, 5, 5, 5, 5 |
| Maxima průchodu zprava: | 5, 5, 5, 5, 4, 3, 3, 2 |
| Výsledné max. výšky: | 1, 3, 3, 5, 4, 3, 3, 2 |
Výsledek už dostaneme snadno – od čísla na i-té pozici v poli maximálních výšek odečteme výšku i-tého decimetru příkopu a tento rozdíl přičteme do výsledného objemu zadržené vody.
Pro příklad výše bychom postupně sečetli hodnoty 0, 0, 1, 0, 0, 2, 0, 0,
takže se zadrží 3 litry vody.
A proč to celé funguje? V každém sloupečku se udrží právě tolik litrů vody, kolik jsme za něj přičetli, tj. rozdíl mezi výškou hladiny a dnem příkopu. Zbývá tedy ukázat, že v poli maximálních výšek máme opravdu uloženou výšku vodní hladiny na dané části. Výška hladiny nemůže být větší, protože jinak by vodě nic nebránilo v odtečení na stranu s nižším maximem. A zároveň se zde voda udrží do této výšky, protože nalevo i napravo je překážka, která sahá alespoň takto vysoko.
Řekněme, že N je délka příkopu, tj. počet čísel na vstupu. Časová složitost je lineární. Při počítání maximálních výšek projdeme vstup třikrát a každé číslo pouze porovnáme s jedním jiným číslem. Při počítání objemu zadržené vody opět projdeme dvě pole o velikosti N a pro každý prvek provedeme konstantně operací. Paměťová složitost je také lineární, neboť si pamatujeme tři pole stejně velká jako vstup.
Tento postup lze ještě vylepšit. Můžeme si všimnout, že při počítání výšek zleva a zprava se hodnoty po přejití globálního maxima (nejvyššího místa příkopu) už nemění, takže do pole s maximálními výškami nikdy nevybereme hodnotu z levé, resp. pravé části. Pojďme se tedy podívat, jak výpočet trošku zrychlit a jak ušetřit paměť.
Nejprve najdeme místo, kde je příkop nejvyšší, a označíme si ho M, tj. M bude označovat pozici, nikoliv výšku. Také se nám bude hodit pomocná proměnná max, ve které budeme počítat maximum z doposud projitých hodnot výšek.
Algoritmus postupně projde jednotlivé části příkopu zleva, dokud nenarazí na nejvyšší místo M. Poté projde příkop zprava, opět do M. Před druhým průchodem je nutné proměnnou max vynulovat.
Pro každou část zaktualizuje proměnnou max (je-li aktuální část vyšší než max, uloží do max současnou výšku) a spočítá, kolik litrů vody se na ní drží. To znamená, že do výsledného objemu přičte rozdíl max a aktuální výšky, takže pokud se nacházíme na doposud nejvyšším bodě, všechna voda odsud odteče, ale pokud ne, nějaká voda se zde zadrží.
Připomeňme, že N je délka příkopu. Hledání nejvyššího místa M zvládneme v čase O(N), protože při jednom průchodu vstupu porovnáme každé dvě sousední výšky a uložíme si větší z nich. Samotný algoritmus vstup projde také pouze jednou a pro každou část vykoná konstantně operací, takže celková časová složitost je O(N). Co se paměti týče, kromě samotného vstupu si pamatujeme pouze pár proměnných.
Na závěr dodáme, že i toto řešení se dá ještě vylepšit tak, abychom celý vstup prošli jen jednou. Na začátku bychom nehledali žádné maximum, ale místo toho bychom si pořídili dvě proměnné pro počítání maxima a dva ukazatele na pozici – jednu dvojici pro procházení zleva a jednu pro průchod zprava.
Na další úsek bychom posunuli ukazatel na té straně, kde je hodnota maxima menší. Do výsledného objemu přičteme to samé jako v předchozím algoritmu – rozdíl maxima a aktuální výšky. Tím spojíme všechny tři fáze (nalezení globálního maxima, počítání průběžných maxim zleva a zprava a počítání výsledku) dohromady.
Ohledně paměti platí to samé, co v předchozím případě. Toto poslední řešení by v realitě vyhrálo v rychlosti, alespoň pokud byste data četli z obrovského souboru na (pomalém) disku. Dva průchody by trvaly dvakrát tak dlouho, tři třikrát, atd.
 28-Z2-6 Kalamita (Zadání)
28-Z2-6 Kalamita (Zadání)
Jako první si uvědomíme jedno velmi důležité pozorování, nikdy se nevyplatí zrušit zastávku, která není listem (tj. není konečná). Proč tomu tak je? Inu, zrušení ne-konečné zastávky zruší i všechny zastávky za ní (viz zadání), tedy i alespoň jednu další (konečnou) zastávku.
To máme jisté kvůli faktu, že graf stanic je strom, tedy neobsahuje žádné kružnice. Přeci jen když nemáme kružnice a vydáme se po nějaké cestě z centrální stanice, třeba přes tu naši rušenou, tak jednou určitě dojedeme na konec, tj. na konečnou stanici. Koneckonců, naše město není nekonečné a absence kružnic zaručuje, že neprojedeme nic dvakrát.
Zrušení zastávky, která není konečná, tedy znamená, že odřízneme od světa lidi jak z té naší zastávky, tak i její odpovídající konečné. A to je určitě víc lidí, než by odřízlo zrušení jen konečné.
Tím jsme přišli na to, že určitě budeme vždycky rušit jen konečné zastávky a zastávky, které se staly konečnými zrušením nějakých předchozích.
Pro jednodušší přemýšlení o zastávkách si ještě uvědomíme, že s centrální zastávkou můžeme počítat jako s úplně normální zastávkou, která má počet lidí nějaké extrémně velké číslo. To nám zajistí, že ji vždycky zrušíme jako poslední. To chceme, jelikož její zrušení automaticky zruší všechny ostatní zbývající zastávky, a tedy je, dle argumentu výše, nevýhodné.
Nyní už si stačí rozmyslet, v jakém pořadí to budeme dělat. I to je ovšem vcelku jasné, zadání nám totiž přikazuje, abychom vždy zrušili tu nejméně zaplněnou zastávku, tedy takovou, která má nejnižší číslo. V tuto chvíli by nás mohlo napadnout najít všechny konečné zastávky, v nich určit tu nejmenší, zrušit ji, znovu najít všechny konečné zastávky, a takhle dokud nám nezbyde jen centrální zastávka.
To by samozřejmě fungovalo, není to ovšem ani zdaleka efektivní řešení. Předně, konečné zastávky není třeba vždy hledat úplně od začátku. Zřejmě nám totiž platí, že jednou konečné zastávky budou konečné i poté, co nějakou odstraníme. A přibýt do klubu konečných může odstraněním nějaké konečné zastávky vždy jen jedna nová, a to konkrétně ta, která se zrušenou zastávkou sousedila.
Dále si také uvědomíme, že z množiny aktuálně konečných zastávek v každé fázi programu jen odstraňujeme minimum a přidáváme jeden prvek, tedy operace, které až nápadně volají po tom, abychom použili minimovou haldu. Pokud náhodou nevíte, co je minimová halda, pak si určitě přečtěte naši kuchařku. Ve zkratce jde ale o datovou strukturu, která po vybudování (trvajícím lineární čas) dokáže v logaritmickém čase vracet nejmenší prvek a jejíž oprava po přidání libovolného prvku trvá taktéž nejhůř logaritmický čas.
Když si dáme tyto dvě úvahy dohromady, tak se konečně dostaneme na ideální řešení. Předně si najdeme všechny konečné zastávky a vytvoříme si z nich minimovou haldu. Jak hledání (stačí prostě projít graf a vedle si pamatovat zastávky, ze kterých už dál jít nelze), tak tvorba haldy nám zabere lineární čas, tedy O(N), kde N je počet zastávek.
Následně vždy z haldy odstraníme minimum za O(log(N)), podíváme se na jejího předchůdce, jestli nám vznikla nová konečná zastávka, a pokud ano, tak jej přidáme do haldy v čase O(log(N))).
Takovýchto kroků, nebo fází chcete-li, provedeme nejhůř tolik, kolik je zastávek. Pokaždé totiž zrušíme jednu zastávku a každou zastávku zrušíme maximálně jednou. Výsledná časová složitost je tedy O(N + N · log(N)), což je stejné jako O(N · log(N)).