Třetí série začátečnické kategorie dvacátého osmého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 14. března v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 28-Z3-1: Místo oslavy
- 28-Z3-2: Zlomkovník
- 28-Z3-3: Posloupnost za trest
- 28-Z3-4: Zbývající úkoly
- 28-Z3-5: Ukotvení stromu
- 28-Z3-6: Šíření drbů
28-Z3-1 Místo oslavy (8 bodů)
Střední škola, na kterou chodí Kevin, slaví tento rok významné výročí: celých 500 let od svého založení. Její vedení proto plánuje uspořádat náležitě velkou oslavu, spojenou s výstavou o historii školy a ukázkami prací studentů.
Než se pustí do dalších příprav, musí se vyřešit jedna důležitá věc. Samotná škola totiž nemá žádné velké prostory, ve kterých by mohla takhle velkou akci uspořádat. Proto si chce někde ve městě pronajmout sál. Ale kde? Ne všechny obyvatele budou oslavy zajímat, a tak by bylo pěkné najít nějaké místo blízké těm, kteří určitě přijdou.
Město tvoří jedna dlouhá rovná ulice, okolo které se nacházejí domy. Pro určení pozice ve městě tedy stačí jediné číslo – vzdálenost od začátku města. Máme k dispozici pozice domů, kde bydlí lidé zajímající se o školní oslavu. Naším úkolem je najít takové místo, které má co nejmenší vzdálenost k tomu, kdo to má nejdále.
Tvar vstupu a výstupu: Na prvním řádku je číslo N, na druhém je N čísel, každé představuje dům zájemce, resp. jeho pozici ve městě. Vypište celé číslo označující nejlepší možnou pozici sálu. Pokud je možných odpovědí více, vypište libovolnou z nich.
5 3 5 17 24 25
14
28-Z3-2 Zlomkovník (10 bodů)
Po nalezení vhodného místa se přípravy rozjely naplno. Kevina nechávalo výročí své školy dlouho chladným (a rýpavě se ostatních ptal, zda 512 let není významnějším výročím než 500), ale pak jeho třída dostala zajímavý úkol. Měli vyrobit nějaké umělecké dílo připomínající Kevinův nejoblíbenější předmět – matematiku.
Jak by taková věc ale mohla vypadat? Kevin dlouho nemohl na nic přijít, ale pak si vzpomněl, jak se Zuzkou po Vánocích odstrojovali stromeček. Co si znovu pořídit strom, ale tentokrát pořádný, matematicky popsatelný? Po chvíli hledání na internetu skutečně našel web, kde prodávali pěkné modely binárních stromů (Nevíte-li, co je binární strom, nahlédněte do naší základní kuchařky.).
| A |
| B |
| A |
| A+B |
| A+B |
| B |
| 1 |
| 1 |
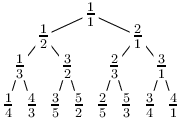
Kevin si nakreslil ještě několik dalších úrovní a došlo mu, že se tímto postupem může dostat k jakémukoliv zlomku v základním tvaru. Jak to ale co nejrychleji provést?
| A |
| B |
R a L, kde R je přechod do pravého a L do levého
syna.
2 5
RLL
28-Z3-3 Posloupnost za trest (10 bodů)
Ajaj! prolétlo Kevinovi hlavou, když uviděl balík se stromem, který nechal poslat na adresu školy. Mělo mu dojít, že ten internetový obchod sídlící na druhém konci planety možná používá jiné jednotky. Očekával výšku okolo dvou metrů, ale tenhle kolos se snad nevejde ani do tělocvičny…
Stěhování obřího zlomkovníku na místo výstavy zabralo půl dne a vystřídal se na něm celý personál školy. Když se ukázalo, že strom je přece jen o něco nižší než výška stropu, všichni si oddechli. A hned poté požádali Kevinova učitele matematiky, aby dal svému nepozornému studentovi nějaký exemplární trest.
Teď je Kevin po škole a zabývá se touto posloupností čísel:
Jak jsme na ni přišli? Začali jsme jednou jedničkou. Pak jsme ji přečetli: „jedna jednička“, takže píšeme jedničku a jedničku. To jsme opět přečetli: „dvě jedničky“, tedy 21. Pak „jedna dvojka, jedna jednička“, čili 1211. A tak dále.
Kevinovým úkolem je zapsat N-tý člen posloupnosti. Ale členy rostou rychle a kdyby byl poctivý, zůstal by ve škole až do večera. Chce si proto pomoci malým podvodem: vypočte jen několik prvních číslic N-tého členu a bude doufat, že matikář delší část kontrolovat nebude.
Pro zadané N a K spočítejte prvních K číslic N-tého členu. Slibujeme, že N,K ≤ 300 000.
8 10
1113213211
28-Z3-4 Zbývající úkoly (12 bodů)
Korejské přísloví říká, že při odložení práce o jeden den uplyne ve skutečnosti dní deset. Kvůli stěhování zlomkovníku a podobným komplikacím čas ubýval a ubýval a s přibližujícím se dnem oslavy zůstávalo mnoho důležitých úkolů nesplněných. Ředitel proto svolal učitele a zástupce žáků k poradě do školní auly.
Když tam Kevin dorazil, schůze už začala a vládl tam zmatek. Učitelé na tabuli vypsali seznam úkolů, které bude třeba před oslavami splnit, a jejich časovou náročnost. Teď se ale nemohli shodnout na tom, zda je vůbec možné všechno stihnout. Problémem je mimo jiné to, že některé úkoly mohou být splněny až po dokončení jiných (např. není možné, aby se instalovala výstava o historii školy, pokud nejsou sepsané texty).
Tvar vstupu: Na prvním řádku dostanete celkový počet úkolů N ≤ 100 000 a počet závislostí K. Na dalším řádku je N čísel, kolik hodin bude splnění jakého úkolu trvat. Na dalších K řádcích se vyskytují dvojice čísel A a B: úkol s číslem B je možné začít až po dokončení úkolu A. Číslujeme od nuly.
Na úkolu může pracovat jen jeden člověk, ale více úkolů lze zpracovávat paralelně (předpokládejte, že dobrovolníků máme k dispozici nekonečně mnoho). Práce na úkolu začne v momentě, kdy všechny úkoly, na kterých závisí, jsou splněné.
Tvar výstupu: Vypište číslo označující počet hodin potřebných k dokončení všech úkolů.
4 4 5 6 8 5 0 1 0 2 1 3 2 3
18
Nejprve je třeba splnit úkol 0, na 1 a 2 se může pracovat současně, teprve po dokončení obou můžeme začít 3.
28-Z3-5 Ukotvení stromu (12 bodů)
Oslava výročí se povedla. Zvláště Kevinův obří zlomkovník vzbudil takovou pozornost, že se na výstavu došlo podívat takřka celé město. Proto se ředitel školy a jeho zástupci jednomyslně shodli na tom, že umělecká díla by se měla vystavit trvale na pozemku před školou.
Nejvíce práce samozřejmě zabralo převezení zlomkovníku. A protože se čekalo, že na novém místě nějaký čas setrvá, bylo nutné jej pořádně ukotvit. To se dělá tak, že se okolo stromu zatluče několik kolíků a od každého vedeme lano až ke kmeni, kde se připevní.
Aby celá konstrukce byla skutečně stabilní, chceme kolíky rozdělit do dvojic, kde oba body a kmen stromu leží v jedné přímce, vzdálenost obou bodů od kmenu je stejná a kmen se nachází mezi kolíky. Můžeme tedy říci, že všechny kotvící body jsou středově souměrné podle bodu označujícího kmen.
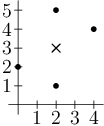
Kevin na místo přišel ve chvíli, kdy pracovníci už zatloukli všechny kolíky a čekali na přivezení stromu. Zapsal si souřadnice jednotlivých kolíků a rád by našel bod, podle kterého jsou všechny středově souměrné – nebo zjistil, že takové místo neexistuje.
Např. pro body [4,4], [2,5], [0,2] a [2,1] je správný střed [2,3], viz obrázek.
28-Z3-6 Šíření drbů (14 bodů)
„Víš, co jsem zjistila? To tvoje veledílo se stejně bude muset brzy přesunout, protože město chce na pozemku dělat archeologické vykopávky!“ řekla Kevinovi Sára. „Vážně? A to jsi zjistila kde?“ zajímal se Kevin. „Od jedné kamarádky,“ odpověděla vyhýbavě.
Sářiny kamarádky ze třídy tvoří nerozlučnou partu a jejich společnou zálibou je drbání o všem možném i nemožném. Každá spolužačka přijde ráno do školy se svým jedinečným drbem. O přestávce se každá z nich zapovídá s kamarádkou dle svého výběru a v těchto dvojicích si povyměňují všechny drby, které v daný okamžik znají.
Znáte celkový počet spolužaček v partě, N. Pro jednoduchost předpokládejte, že N je mocnina dvojky (1, 2, 4, 8, 16, …). Navrhněte, o které přestávce se má setkat kdo s kým tak, aby se co nejrychleji všechny kamarádky dozvěděly všechny drby.
Např. pro čtyři spolužačky A, B, C, D si mohou o první přestávce vyměnit drby dvojice A–B a C–D, o druhé pak A–C, B–D. Takto bude po dvou přestávkách znát každá všechny drby.