Maximální párování v bipartitním grafu

Článek si můžete také prohlédnout vysázený v PDF.

Všichni jistě znáte základní axiom laciných romantických příběhů: každý člověk, bez ohledu na to, jak usilovně se (vědomě či nevědomě) pokouší o opak, nakonec vždy nějakým řízením osudu potká „toho pravého/tu pravou“. Upřímně, Osud je z tohoto nově přiřknutého úkolu trochu nešťastný. Vůbec netuší, jak by takovou věc měl udělat. Naštěstí se v nudných chvílích bavil řešením KSP (osobně žádné neposlal, ale kdo ví za kolika nápady stojí v pozadí...) a ví, že s trochou šikovné manipulace se celý svět dá použít jako opravdu výkonný počítač.

Pro začátek by Osud rád věděl, koho vůbec s kým dohromady dávat. Předpokládejme, že má pro každou dvojici lidí k dispozici informaci o tom, zda jsou k sobě kompatibilní (jedna osoba může být kompatibilní s více různými lidmi). To si můžeme znázornit grafem: vrcholy jsou všichni lidé na Zemi a hrany spojují kompatibilní dvojice. Případné menšiny mezi řešiteli jistě odpustí, budeme-li pro jednoduchost přepokládat, že je tento graf bipartitní. (Tento text vyžaduje znalost pojmů jako graf, bipartitní graf či prohledávání do (šířky / hloubky). Pokud je slyšíte poprvé, doporučujeme nejprve nahlédnout do naší grafové kuchařky.)

Osud by rád z lidí vytvořil páry takové, že každý pár je tvořen dvojicí kompatibilních lidí a žádná osoba nepatří do víc než jednoho páru. Tomu odpovídá pojem párování v grafu, což je podmnožina jeho hran taková, že žádné dvě nesdílí společný vrchol. Pochopitelně nepůjde spárovat všechny: třeba už protože partity nejspíš nebudou stejně velké. Místo toho budeme chtít najít párování maximální, tedy tvořené největším možným počtem hran (spokojených párů).

Následující obrázek zobrazuje graf a jedno jeho možné maximální párování (mající, stejně jako všechna ostatní maximální párování v tomto grafu, velikost 5):

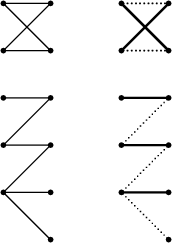
Zlepšující cesty

Budeme postupovat tak, že začneme s prázdným párováním (spárován není nikdo) a budeme ho postupně zlepšovat, dokud nebude maximální. Jednoduché je párování zlepšit, pokud existuje dvojice kompatibilních nespárovaných jedinců. Takovou hranu můžmeme do párování prostě přidat, čímž ho zvětšíme a neporušíme při tom žádnou z podmínek. Pokud taková dvojice neexistuje, znamená to, že párování zlepšit nejde? Rozhnodně ne. Uvažte následující graf (plné čáry značí páry, tečkované kompatibilitu):

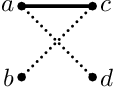
Pokud bychom a spárovali s d, uvolní se nám c ke spárování s b. Jak takovou myšlenku zobecnit? Zavedeme několik pojmů: (ne)párovací hrana je hrana původního grafu (ne)patřící do aktuálního párování, volný vrchol je takový, který není spárován (všechny hrany s ním incidentní jsou nepárovací), střídavá cesta je cesta v grafu, na které se střídají párovací a nepárovací hrany, a nakonec zlepšující cesta (též volná střídavá cesta) je střídavá cesta začínající a končící volným vrcholem (a tedy nutně i nepárovací hranou).

Například v grafu výše existuje jediná zlepšující cesta, b - c - a - d. Není těžké si všimnout, že pokud na nějaké zlepšující cestě prohodíme hrany (z nepárovacích hran uděláme párovací a naopak; též se na to dá dívat tak, že původní párování „přexorujeme“ touto cestou), výsledek bude stále párování, ale o jedna větší.

Teď bychom rádi dokázali, že takovéto zlepšování už stačí: tedy že kdykoli máme párování, které není maximální, existuje v něm zlepšující cesta. Mějme nějaké párování P, které není maximální a nějaké jiné párování M, které maximální je. Představme si, že obě párování položíme „přes sebe“. Zahodíme všechny hrany, které nepatří ani do jednoho párování, nebo patří do obou. Zbude nám graf mající řekněme modré (patřící jen do párování M) a purpurové (patřící jen do párování P) hrany. Tedy vlastně jakýsi rozdílový graf: modře jsou označeny hrany, které má M navíc oproti P, a purpurově ty, jež má P navíc oproti M.

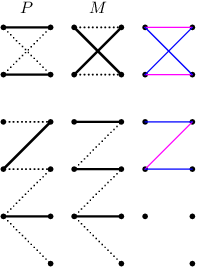
Všimněme si, že tento graf se nemůže nikde větvit (všechny jeho vrcholy mají stupeň nejvýše 2). Kdyby existoval nějaký vrchol stupně ≥ 3, povedou z něj dvě hrany stejné barvy, což by znamenalo, že příslušné párování obsahuje dvě hrany sdílející vrchol. Tedy všechny komponenty souvislosti tohoto grafu jsou cesty nebo kružnice, navíc se na nich vždy střídají barvy (ze stejného důvodu). To automaticky znamená, že všechny kružnice mají sudou délku a obsahují stejný počet hran z obou párování. Protože předpokládáme, že M je větší než P, musí být v grafu více modrých hran než purpurových. Tedy musí existovat alespoň jedna komponenta mající převahu modrých hran a už víme, že to bude cesta. Jelikož se barvy střídají, aby bylo modrých více, musí cesta začínat i končit modrou hranou.

Taková cesta odpovídá zlepšující cestě v P: střídají se na ní hrany obsažené v P (purpurové) a neobsažené v P (modré) a oba koncové vrcholy jsou volné (snadné cvičení). A tím je dokázáno.

Algoritmus

Z výše řečeného už přímo plyne triviální algoritmus na hledání maximálního párování:

  1. P ← prázdné párování
  2. Opakuj:
  3.         Zkus najít zlepšující cestu (jednoduchá aplikace DFS).
  4.         Pokud existuje, přexoruj s ní P.
  5.         Pokud ne, vrať P jako maximální párování.

Jedno hledání zlepšující cesty trvá O(|E|) a provedeme jich |M|, kde |E| je počet hran grafu a |M| velikost maximálního párování. Maximální párování tedy umíme najít v čase O(|M||E|), a jelikož |M| ≤ |V| (počet vrcholů grafu), můžeme jej shora odhadnout O(|V||E|).

Tento jednoduchý algoritmus pochopitelně není nejrychlejší. Použitím jen o málo složitějšího Hopcroftova-Karpova algoritmu můžeme dosáhnout složitosti O(|E|√|M|), resp. O(|E|√|V|).

Závěrem ještě jedna poznámka pro ty z vás, kdož znáte toky v sítích: popsaný algoritmus je naprosto ekvivalentní Ford-Fulkersonovu algoritmu spuštěnému na párovací síť. Zlepšující cesty, jak jsme si je zde definovali, přesně odpovídají tokovým zlepšujícím (někdy též nenasyceným) cestám.

Článek pro vás sepsal

Filip Štědronský