Druhá série třináctého ročníku KSP

Zadání úloh

13-2-1 Sirky (10 bodů)

Pat a Mat hrají spolu následující hru (kupodivu nemá se šachy nic společného): Na stole leží hromádka s N sirkami. Hráči se střídají v tazích. V každém tahu může hráč odebrat z hromádky libovolný počet sirek ve tvaru 2i*3j*5k, kde i, j a k jsou nezáporná celá čísla. Hráč, který odebere poslední sirku vyhrává.

Mat pořád prohrával, a tak vás požádal, abyste mu napsali program, který by mu poradil, jak na Pata vyzrát. Váš program tedy dostane na vstupu počet sirek na hromádce. Po jeho načtení vypíše, jak má Mat táhnout a zeptá se, jak táhl Pat. Pak opět poradí tak Matovi…

Příklad: Na hromádce je 8 sirek.

Rada Matovi: 1
Pat: 4
Rada Matovi: 3
Mat vyhral!

Řešení

13-2-2 Přetlačovaná (12 bodů)

Při studiu starých knih narazil pan Filogam na hru Přetlačovaná. Ta se hraje na herním plánu ve tvaru čtvercové sítě. Hráči střídavě kladou své kameny (první hráč červené, druhý zelené) na dosud neobsazená křížení. Situace na hracím plánu se nazývá vyrovnaná, pokud v každém řádku a každém sloupci má jeden hráč nejvýše o jeden kámen více než hráč druhý. Pan Filogam nalezl v knize zakreslenou jednu pozici hry, o které je v knize napsáno, že je vyrovnaná. Pan Filogam tomu ovšem nevěří, a protože za dlouhá léta už barvy vybledly, není možné jednoduše přepočítat počty kamenů v jednotlivých řádcích a sloupcích. Obrátil se proto na vás, abyste mu pomohli.

Vaším úkolem je napsat program, který na vstupu dostane počet kamenů na herním plánu a jejich souřadnice a vypíše, zda pozice skutečně mohla být vyrovnaná – tzn. zda exituje obarvení kamenů takové, že v každém řádku a každém sloupci se bude počet červených a zelených kamenů lišit nejvýše o jedna. Pokud takové obarvení kamenů existuje, má ho váš program vypsat.

Příklad: Na herním plánu jsou 4 kameny na pozicích (0, 0), (0, 1), (1, 1) a (2, 1). Řešením je třeba obarvit kameny 1 a 3 zelenou a kameny 2 a 4 červenou.

Řešení

13-2-3 Kamiony (10 bodů)

Firma Doleva & Doprava se zabývá kamionovou přepravou na větší vzdálenosti. Délku trasy kamionu budeme značit D. Kamion ujede na nádrž plnou nafty K kilometrů. Na trase je N čerpacích stanic. Pro každou stanici i je dána její vzdálenost od počátku trasy ai a cena ci nafty na jeden kilometr v této stanici (kamion může samozřejmě načerpat pouze část nádrže). Vaším úkolem je navrhnout zastávky u čerpacích stanic a množství načerpané nafty tak, aby cesta vyšla firmu co nejlevněji. Předpokládáme, že na počátku kamion vyjíždí s plnou nádrží.

Příklad: Trasa má délku 800 km. Kamion ujede na plnou nádrž 300 km. Na trase jsou 4 čerpadla ve vzdálenostech 200, 300, 500 a 600 km od počátku trasy. Ceny nafty na čerpadlech jsou po řadě 10, 40, 20 a 10.

Kamion pojede k čerpadlu 1, kde načepuje na 200 km. Pak k čerpadlu 3, kde načepuje na 100 km a nakonec k čerpadlu 4, kde načepuje na 200 km.

Řešení

13-2-4 Mraveniště (10 bodů)

V jednom mravenčím království u Jáchymova se dostala k moci osvícená mravenčí královna. Tato královna se rozhodla poněkud vylepšit dopravní situaci ve svém mraveništi.

V mraveništi jsou jednotlivé komůrky (očíslujeme si je od 1 do N), které jsou propojené chodbičkami. Každá chodbička je jednoznačně určena dvojicí komůrek, mezi kterými vede (předpokládáme, že chodbičky se protínají pouze v komůrkách). Královnu by pro začátek zajímalo, jak dlouhá je nejkratší cesta mezi dvěma komůrkami. Má to ovšem jeden háček. Mravenčí počítač má velmi omezenou paměť a mraveniště je veliké. Nemůžete si tedy pamatovat všechny komůrky, natož pak všechny chodbičky (tzn. paměťová složitost vašeho algoritmu by měla být lepší než lineární vzhledem k počtu komůrek). Abyste vůbec mohli zjistit, jak vlastně mraveniště vypadá, můžete se vždy obsluhujícího mravence zeptat, zda mezi danými dvěma komůrkami vede chodbička či nikoliv.

Příklad: Počet komůrek je 4, zajímá nás délka nejkratší cesty mezi komůrkami 1 a 3.

Dotazy:
1 3: Ne
1 2: Ano
2 3: Ano

Nejkratší cesta mezi komůrkami 1 a 3 má délku 2.

Řešení

13-2-5 LISP (10 bodů)

Vaším úkolem v druhém pokračování našeho seriálu bude napsat funkci cut, která dostane na vstupu vyhledávací strom a dvojici čísel určujících interval. Vaše funkce by měla vrátit vyhledávací strom, ze kterého budou vypuštěna všechna čísla mimo zadaný interval.

Binární strom je datová struktura složená z uzlů. V každém uzlu jsou uloženy odkazy na dva uzly – levého a pravého syna (jeden z odkazů odkaz či oba odkazy mohou být nastavené na Nil, pokud příslušný syn neexistuje). Binární strom pak můžeme nadefinovat následovně:

Vyhledávací stromy mají navíc v každém uzlu číslo. Pro toto číslo platí, že čísla ve všech uzlech v levém podstromu jsou menší a čísla ve všech uzlech v pravém podstromu jsou větší.

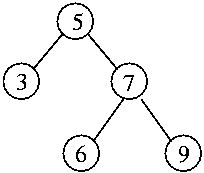
V LISPu budeme uzel vyhledávacího stromu reprezentovat ve tvaru (číslo.(levý syn.pravý syn)).

Příklad: (cut (5 . ((3 . (nil . nil)) . (7 . ((6 . (nil . nil)) . (9 . (nil . nil)))))) 4 6) má vrátit (5 . (nil . (6 . (nil . nil)))).

Vyhledávací strom z příkladu
Vyhledávací strom z příkladu

Pokud si své programy chcete vyzkoušet, můžete si stáhnout interpret Ksp-Lispu (tar, ZIP).

Řešení