Pátá série začátečnické kategorie třicátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
 37-Z5-1 Tramvaj (Zadání)
37-Z5-1 Tramvaj (Zadání)

Pro řešení nám stačí celou situaci krokově odsimulovat. Budeme si hlídat tři proměnné: aktuálně kontrolovanou zastávku, čas pohybu tramvaje a čas pohybu Kevina.
Začneme tím, že spočítáme dobu přesunu tramvaje z depa do Kevinovy počáteční zastávky Z – na těchto místech Kevin určitě nemůže nastoupit, takže nemá cenu tyto případy kontrolovat.
Poté ve smyčce pro každou hodnotu od zastávky Z vypočítáme, ve kterém čase by do příští zastávky dorazila tramvaj (pouhým přičtením hodnoty ze seznamu) a kdy Kevin (přičtením téže hodnoty vynásobené zpomalovacím faktorem). Jakmile je čas příjezdu tramvaje větší než čas příchodu Kevina, smyčku ukončíme a vypíšeme číslo zastávky, kde jsme zrovna skončili. Pokud má Kevin ještě náskok, opakujeme tento postup pro další zastávku s aktualizovanými hodnotami trvání pohybů.
Tímto způsobem docílíme lineární časové složitosti; v nejhorším případě budeme muset zkontrolovat téměř celý seznam až do předposlední zastávky, kde máme slíbeno, že se Kevin sveze. Pokud jsme si na začátku programu načetli celý vstup, bude i paměťová složitost lineární, šlo by však dosáhnout konstantní: Celou dobu si v paměti musíme držet pouze hlídané proměnné a konstantu pro zpomalování Kevina. Protože nás v daný moment zajímá pouze jedna doba přesunu, šlo by tyto hodnoty načítat dynamicky ve smyčce.
 37-Z5-2 Závorky (Zadání)
37-Z5-2 Závorky (Zadání)
Jako první se hodí zamyslet se nad tím, jak vlastně budeme doplňovat závorky do původního řetězce.
Třeba když máme na vstupu )())(((, nabízí se nám hned několik způsobů, třeba ()()()()()(),
()(())(())(), nebo i (()())((())).
První možnost vypadá nejlépe, ale není příliš praktická, protože při vkládání závorky doprostřed řetězce se musí posunout všechny ostatní prvky, což znamená, že jedno vkládání může trvat až O(N) času. Tomuto problému se můžeme částečně vyhnout tím, že začneme prázdným řetězcem a budeme postupně přidávat na konci vhodnou závorku, podle toho, co je na vstupu, ale nabízí se ještě jednodušší řešení.
Koukneme se na poslední možnost a všimneme si, že se skládá ze dvou přidaných levých závorek, poté celého původního vstupu za sebou a na konci jsou přidané pravé závorky. Přeci když správné uzávorkování je definované tak, že má levé závorky nalevo od svých příslušných pravých závorek, tak můžeme všechny nové levé závorky připlácnout na začátek vstupu a všechny pravé závorky na konci vstupu.
Teď už jen zbývá otázka, kolik přesně těch závorek musíme přidat. Toto zvládneme tak, že si budeme pamatovat rozdíl počtu levých a pravých závorek při čtení vstupu. Tedy budeme postupně číst vstup, a když narazíme na levou závorku, přičteme jedničku, a když narazíme na pravou závorku, odečteme jedničku.
Pokud bychom narazili na případ, kde po odečtení jedničky bude rozdíl záporný, znamená to, že jsme narazili na pravou závorku bez příslušné levé závorky. Z toho vyplývá, že musíme přidat nalevo levou závorku, a protože tu závorku plánujeme přidat, rovnou ji do rozdílu započítáme a zůstane nezáporné.
Poté co dočteme vstup, výsledný rozdíl v počtu závorek nám řekne kolik levých závorek ještě nemají příslušnou pravou, tedy kolik pravých závorek musíme přidat, aby bylo uzávorkování správné. Výsledné uzávorkování jednoduše získáme sloučením příslušného počtu levých závorek, původního vstupu a příslušného počtu pravých závorek.
Všimněme si, že levé závorky přidáváme pouze když narazíme na pravou závorku bez příslušné levé závorky, a taktéž pravé závorky přidáváme pouze pro zbývající levé závorku bez příslušné pravé závorky. Zjevně tyto závorky jsou potřeba přidat, aby bylo uzávorkování správné, a protože nepřidáváme žádné další závorky, uzávorkování bude co nejkratší.
Celý algoritmus prochází vstup délky N jednou a u každé závorky provádíme pouze konstantní počet kroků (buď odečítání nebo přičítání k uložených hodnot). Tedy celé běží v čase O(N).
 37-Z5-3 Krabice na pásech (Zadání)
37-Z5-3 Krabice na pásech (Zadání)
Podle zadání máme souřadnice jedné krabice a chceme zjistit, kde se bude nacházet v čase T. Přímočarý přístup k řešení je simulace pohybu krabice, protože krabice má jenom jednu možnost, kam se může nedobrovolně vydat. Začneme na startovní pozici a v každém z T časových kroků (sekund) aktualizujeme pozici krabice podle směru pásu na jejím aktuálním políčku a pokračujeme, dokud nám nedojde čas.
Zadání nás ale varuje, že T může být hodně veliké, takže nemůžeme simulovat celý pohyb krabice krok po kroku. Naštěstí je ale velikost továrny omezená, a tedy někde musí vzniknout cyklus. Navíc si musíme uvědomit, že krabice nemusí začínat v cyklické části pásů, jak ilustruje obrázek. Když zjistíme délku cyklu, tak nám stačí odečíst délku cesty k cyklu od T a pak spočítat zbytek po dělení T délkou cyklu a dokončit simulaci pouze na tento zbytek.
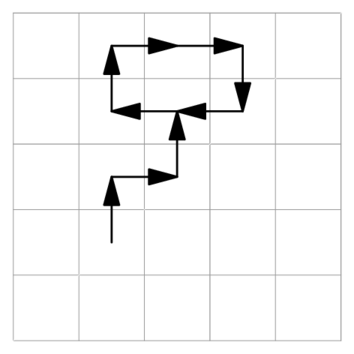
Ale jak najít délku cyklu? Nejjednodušší je pamatovat si, která políčka na mapě jsme již navštívili a kdy. Pokud se dostaneme do již navštíveného políčka, tak víme, že jsme v cyklu. Teď už jen zjistíme, jak dlouhý cyklus je, a to tak, že odečteme čas, kdy jsme na daném políčku byli poprvé, od aktuálního času. Protože krabice se pohybuje jenom jedním směrem, tak jsme cyklus určili jednoznačně. Teď už jen provedeme operaci modulo pro získání zbývajícího času a dokončíme simulaci s tímto zbytkem.
Tímto způsobem jsme schopni najít pozici krabice i pro velké T v nejhorším čase O(R ·S). Nejhorší případ nastane, pokud je celá továrna jeden cyklus a detekujeme ho až po celém průchodu.
Upozorňujeme, že se svět neshodne v implementaci modula. V některých jazycích (třeba C, C++, …) se liší pro záporné operandy. Operace a % b vrací zbytek po dělení, jehož znaménko se řídí znaménkem dělence a. Pokud potřebujete, aby zbytek byl vždy nezáporný, můžete použít ((a % b) + b) % b. Naopak třeba v Pythonu operace % funguje tak, že vrací nezáporný zbytek.
 37-Z5-4 Vedení elektřiny (Zadání)
37-Z5-4 Vedení elektřiny (Zadání)
Naše úloha mluví o grafech, a tedy grafovou terminologii budeme hojně používat. Pokud se s grafy ještě neznáte, doporučujeme nahlédnout do příslušné kuchařky.
V naší úloze máme neorientovaný graf, kde města odpovídají vrcholům a vedení hranám. Poté chceme, aby z každého města existovala cesta do libovolné elektrárny. Když se podíváme na jednotlivé komponenty souvislosti našeho grafu, tak je můžeme rozdělit na ty, které elektrárnu mají a ty, které ne. V komponentách s elektrárnou jsou všechna města propojena, takže zbývá vyřešit jen komponenty bez elektrárny.
Tam budeme určitě potřebovat postavit další vedení. Uděláme to, že si vybereme libovolný vrchol z každé komponenty bez elektrárny, a propojíme ho s vrcholem s první elektrárnou. Tím pádem budeme potřebovat tolik vedení, kolik je komponent bez elektrárny.
A proč je tohle optimální? Představme si libovolné řešení a všimněme si, že každé přidané vedení sníží počet komponent bez elektrárny nejvýš o jedna:
- Buď vede v rámci jedné komponenty. Pak se komponenty nemění.
- Pokud vede mezi komponentou s elektrárnou a komponentou bez, tak jednu bez zrušíme a počet se sníží o jedna.
- Anebo vede mezi dvěma komponentami bez elektráren. Potom počet opět klesne o jedna.
- A na závěr, pokud vede mezi dvěma komponentami s elektrárnou, tak se počet komponent bez elektráren nezmění.

Nyní pojďme dát dohromady algoritmus:
- Použijme rozdělení na komponenty souvislosti popsané ve výše zmíněné kuchařce (viz kapitola Prohledávání do hloubky).
- Projdeme vrcholy v každé komponentě a buď mezi nimi najdeme elektrárnu, nebo si uložíme libovolný vrchol z této komponenty.
- Na závěr postavíme vedení mezi každým uloženým vrcholem a první elektrárnou.