Čtvrtá série šestnáctého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 16-4-1: Mnichova posedlost
- 16-4-2: Technologické trable
- 16-4-3: Stávka programátorů
- 16-4-4: Dlouhoprstova zapeklitá hra
- 16-4-5: Obchodníci s deštěm
- 16-4-6: Šikmá věž v Kocourkově
16-4-1 Mnichova posedlost (Zadání)
Řádění Askejťáka mnichy zmátlo natolik, že nechali nápravu pouze na Vás. Ovšem často jenom čekali a čekali a spali a čekali…Nakonec se na nekonečné posouvání disků nemohl dívat ani sám Bůhdha a rozhodl se přispět svou troškou k nápravě toho, co jeho příbuzný Kazisvět napáchal.
Začněme jednoduchým pozorováním: věž je vždy nejlepší postavit na tom kolíku, kde leží největší disk. Kdybychom ji chtěli postavit na jiném kolíku, museli bychom všech N-1 disků přesunout na nějaký volný kolík, pak přesunout největší disk na cílový kolík a pak na něj přesunout zbytek disků. Nicméně v tom stavu, kdy bylo všech N-1 disků na nějakém volném kolíku a největší disk nebyl dosud přesunutý, jsme mohli rovnou přesunout N-1 disků na ten největší a ušetřit tak jedno přesunutí (největšího disku).
Dále bychom potřebovali vědět, na kolik přesunutí dokážeme přemístit věž o m discích na jiný kolík. Označme tento počet T(m) (evidentně T(1)=1). Když tedy chceme přesunout věž o m discích na jiný kolík, musíme nejprve m-1 disků přesunout na volný kolík, největší disk přesunout na cílový a zbylých m-1 disků vrátit zpátky na největší disk. Toto jednoduché pozorování se dá vyjádřit takto: T(m) = T(m-1) + 1 + T(m-1) = 2T(m-1) + 1. Po chvilce počítání zjistíme, že T(m) = 2m-1.
Vyzbrojení (Bůhdhou) těmito dvěma pozorováními můžeme se směle pustiti do našeho původního problému. Budeme si pro každý disk i počítat, kolik přesunů by nám zabralo postavit věž s disky i,… ,N na každý z kolíků 1,2,3. Tuto hodnotu můžeme značit Tahy(i,k), kde k je číslo kolíku. Ještě si K(i) označme, na jakém kolíku je i-tý disk.
Je jasné, že hledaná hodnota je Tahy(1,K(1)). Jak ale tyto hodnoty počítat? Pro jediný disk určitě platí, že na nějakém kolíku už je, nebo ho tam mohu přesunout jediným tahem, tedy Tahy(N,k=K(N))=1 a Tahy(N,k≠ K(N))=0.
Pokud chceme přesunout disky od i-tého až po nejmenší (N-tý) na kolík k, můžou nastat dva případy. Buď je i-tý disk na kolíku k a pak je nutné přesunout zbylé disky na kolík k, čili Tahy(i,k=K(i))=Tahy(i+1,k). Nebo disk i na tomto kolíku neleží a pak je nutné přesunout disky od (i+1)-ního na volný kolík pom (ani k ani K(i)), disk i přesunout na kolík k a pak všechny disky od (i+1)-ního vrátit na kolík k, čili Tahy(i,k≠ K(i))=Tahy(i+1,pom) + 1 + T(N-i)=Tahy(i+1,pom)+2N-i.
Z toho plyne řešení s lineární časovou složitostí. Budeme počítat jednotlivé hodnoty Tahy(i,k) pro i=N,… ,1 a nakonec vypíšeme hodnotu Tahy(1,K(1)). Takto by byla paměťová složitost také lineární. Nicméně můžeme si všimnout toho, že hodnotu Tahy(i,k) potřebujeme jen k výpočtu hodnot Tahy(i-1,k) – čili není nutné si pole Tahy pamatovat celé, ale stačí nám aktuální dva řádky. Pokud by vstupní data byla čísla kolíků, na kterém leží disky N,… ,1, bude paměťová složitost konstantní.
Ještě poznámka k došlým řešením – málokdo vzal v úvahu, že počet přesunů může být až 264-1 a že se tedy nejspíš nevejde do běžného 32-bitového čísla. Nicméně většina dnešních jazyků 64-bitové čísla podporuje a tak stačilo použít příslušný 64-bitový typ.
Navíc mnozí řešitelé používali při výpočtu mocniny dvojky a tak si je
předpočítali do pole. To ale není vůbec třeba, protože jak v Pascalu tak v Céčku
existují operace bitového posunu, který se dá použít přesně k tomuto výpočtu:
2i=1 << i=1 shl i.
 Ve zkratce: víme, kde má skončit největší disk. Končíme tedy tím, že přesuneme druhý
největší disk (evidentně také z místa, kde byl na začátku) na první a ze zbylého
kolíku pak přestěhujeme všechny zbylé disky nad druhý disk. Jinými slovy
potřebujeme 2N-2 tahů + tahy na složení zbylých disků na zbylý kolík, což
je ale ta samá úloha (oba velké disky nám v tom nemohou nijak překážet). Takže
můžeme všechny disky zpracovat pozpátku v konstantním prostoru, lineárním čase a
jednom řádku programu (viz). –M.M.
Ve zkratce: víme, kde má skončit největší disk. Končíme tedy tím, že přesuneme druhý
největší disk (evidentně také z místa, kde byl na začátku) na první a ze zbylého
kolíku pak přestěhujeme všechny zbylé disky nad druhý disk. Jinými slovy
potřebujeme 2N-2 tahů + tahy na složení zbylých disků na zbylý kolík, což
je ale ta samá úloha (oba velké disky nám v tom nemohou nijak překážet). Takže
můžeme všechny disky zpracovat pozpátku v konstantním prostoru, lineárním čase a
jednom řádku programu (viz). –M.M.
16-4-2 Technologické trable (Zadání)
Kuchařka a počet bodů svádí k tomu, abychom na naše pole prostě napasovali binární vyhledávání a hotovo. Jenže základní problém se světem je ten, že krokodýla štěkat nenaučíš a půlením nekonečna se ke konstantě nedobereš (a tedy ani k hledané hodnotě).
Proto budeme muset nejprve vyřešit tři problémy:
- Vzhledem k čemu měřit časovou složitost, jestliže pole ve kterém hledáme je nekonečné.
- Když se standardně uvažuje o časové složitosti operací na poli (orání), bere se vzhledem k jeho velikosti – to v našem případě zřejmě není použitelná cesta, navíc přímo v zadání je dáno, že pole nemáme považovat za vstup.
- Další možnost by byla měřit ji vzhledem k hodnotě hledaného čísla, které je skutečným vstupem, o což se někteří z vás pokusili. Žel bohu, čísla se mohou v poli opakovat, takže pro libovolně rychlý algoritmus hledání stejného nebo vyššího čísla vymyslím takové pole, že místo výsledku dostanete kopřivku.
- Zbývá tedy použít index N hledaného čísla x v poli, byť ze zadání nejsme schopní o jeho velikosti nic říci.
- Žádný algoritmus v principu nemůže být konečný, neboť u nekonečného pole plného jedniček nemáme šanci zjistit, že se v něm hledaná dvojka nevyskytuje. Proto naše odhady budou platit pouze pro případ, kdy algoritmus skončí.
- Jak naučit krokodýla štěkat. (Haf!)
A jak tedy hledat?
Jediné co o posloupnosti čísel v poli vím, je, že je neklesající. Dále mohu dotazem zjistit konkrétní hodnotu v určité buňce. Z toho však nemohu nic usoudit o rychlosti růstu v neprobádaných oblastech – z tohoto důvodu byly všechny vaše snahy o nástřel pozice hledaného čísla na základě hodnot buněk marné (vzhledem k nejhoršímu možnému odhadu, a o ten nám jde). Zbývá nám využít monotonii – každý dotaz na buňku nám dává pouze informaci, ve které polovině pole vůči buňce se hodnota nalézá – zabývat se druhou částí pole je čiré plýtvání, neb se nic nového nedovíme.
Podtrženo sečteno, jde o to, jak se pomocí půlení intervalu co nejrychleji dostat k hledané hodnotě. Každý dotaz nám řekne, v které polovině pole hledat, což nás dovede k tomu, že první fáze algoritmu se týká nalezení stejné nebo vyšší hodnoty než je hledaná. Všimněte si, že pokud by se jednalo pouze o tuto úlohu, je otázka optimality neřešitelná – ke každému algoritmu najdu ještě rychlejší. Jenomže nám se bude stávat, že najdeme číslo, které je vyšší, a tak nastane druhá fáze – klasické binární vyhledávání v intervalu I ohraničeném posledními dvěma dotazy. Následuje další pozorování – čím rychlejší bude první fáze, tím větší budou intervaly mezi jednotlivými dotazy, a tedy i poslední interval pro druhou fázi (BÚNO předpokládám, že poslední interval není kratší než intervaly předchozí). S pomocí půlení intervalů – a nic víc dotazem na buňku nezjistím – jsem v i-tém kroku schopen zúžit prohledávaný interval I na I/2i, což dává složitost log2 I pro druhou fázi.
Nyní rozeberme složitosti pro vybrané strategie v první fázi:
- Pokud budu hledat pravý konec intervalu přičítáním konstanty k ku indexu, bude nám první fáze trvat O(N), druhá fáze O(log k)=O(1); celkově O(N).
- Pokud budu hledat pravý konec násobením indexu konstantou k, bude první fáze trvat ⌈ logk N⌉ a druhá fáze dostane interval délky ≤ (k-1)·N, na kterém bude hledání trvat O(log2 (k-1) + log2 N); celkově tedy O(log N).
- Pokud budu hledat pravý konec v čase O(F(N)), kde F je asymptoticky pomalejší než log N, dostane druhá fáze interval IF a bude trvat O(log IF), což se bude rovnat O(log N) pouze v případě, že IF není větší než mocnina N. Příkladem strategie, kdy se interval ještě vejde do mocniny, je násobení indexu sebou samým místo konstanty (O(log N2)=O(log N)). Příkladem strategie, kdy se do mocniny nevejdeme, budiž výpočet dalšího indexu pomocí Ackermannovy funkce – v takovém případě se nám druhá fáze obecně dostane nad logaritmus.
Z hlediska asymptotického chování je optimum na složitosti O(log N), šťourové zajímající se o optimalitu počtu dotazů do pole bez zanedbávání multiplikativních konstant mohou začít zkoumat vzájemnou závislost F a IF.
Někteří z vás řešili, jak je to s paměťovou složitostí, jestliže budu chtít ukládat velké indexy nekonečného pole. Uvědomte si, že tento problém nastává i za normální situace, kdy je velikost pole n – zjevně s velikostí n bude muset růst i rozsah hodnot, které jsme schopni uložit v registru. Na to jsou dvě možné odpovědi:
- Standardní: předpokládáme nezáludnost programátora a do každého registru mu dovolíme uložit libovolně velké číslo. Nezáludnost spočívá v tom, že ho nenapadne do tohoto registru začít nějak kódovat další informaci – každý program bychom pak mohli spočítat pomocí konstantní paměťové složitosti.
- Pro záludné přestaneme počítat paměťové buňky na čísla a začneme počítat bity. Každý registr pak dostane paměťovou složitost log n; zvedne se také dosud konstantní složitost na atomické operace s registry atd. Celkově se proto zvýší odhady složitostí jednotlivých algoritmů, nicméně stále nám zůstane schopnost porovnávat rychlosti jednotlivých algoritmů mezi sebou.
V implementaci je použito přímo pole; považuji-li přístupy do něj za dotaz na uživatele, je paměťová složitost konstantní; nenechte se mýlit céčkem, pole začíná od indexu 1.
 Šťoura se hlásí o slovo. Nejprve si uvědomme, že Šandíkův dvojfázový algoritmus je vlastně
jediný možný: položíme-li první dotaz a zjistíme, že číslo v poli je menší než
hledaná hodnota, nemá se smysl dále ptát na cokoliv před ní, analogicky pro
další dotazy, takže musíme jít doprava, dokud nedostaneme větší hodnotu. Ale
jakmile ji dostaneme, zase víme, že hledané číslo je mezi touto hodnotou a
předchozím dotazem, a tady už je optimální binární vyhledávání.
Šťoura se hlásí o slovo. Nejprve si uvědomme, že Šandíkův dvojfázový algoritmus je vlastně
jediný možný: položíme-li první dotaz a zjistíme, že číslo v poli je menší než
hledaná hodnota, nemá se smysl dále ptát na cokoliv před ní, analogicky pro
další dotazy, takže musíme jít doprava, dokud nedostaneme větší hodnotu. Ale
jakmile ji dostaneme, zase víme, že hledané číslo je mezi touto hodnotou a
předchozím dotazem, a tady už je optimální binární vyhledávání.
Co se optimálního počtu dotazů týče: co to vlastně znamená optimální? Libovolný algoritmus můžeme přeci pro prvních n hodnot zlepšit až na ⌊ log2 (n-1) ⌋+ 2 tím, že první dotaz bude na n-tý prvek a pokud je hledaná hodnota menší, spustíme půlení intervalu, jinak přepneme na původní algoritmus, který jsme tím na ostatních prvcích o konstantu zlepšili. Naopak pokud v uvedeném algoritmu s k-násobením zvolíme větší k, bude nám první fáze trvat log2 k-krát rychleji a druhou si tím zpomalíme jen o konstantu log2 (k-1), čili jsme algoritmus zrychlili všude až na prvních několik hodnot. Analogicky místo libovolné funkce F můžeme použít funkci o konstantu pomalejší. Docházíme tak k překvapivému závěru, že ke každému algoritmu můžeme najít takový, který pro vybrané hodnoty bude o něco rychlejší. Ale na druhou stranu, alespoň log2 n je určitě potřeba, takže dokud nás nezajímají multiplikativní konstanty, je O(log n) dozajista optimální. Haf! –M.M.
16-4-3 Stávka programátorů (Zadání)
Stávková reportáž televize CNN nedopadla úplně tak, jak její majitel čekal. Byla to vlastně docela katastrofa. Jedni dali řidičovi filmového vozu radu, ať chvíli počká, že to hned v momentě vyřeší (a jestli neumřeli, řeší dodnes). Jiní ho instruovali, aby si vybral vždy cestu, která je nejkratší, takže ho všichni ostatní (lépe instruovaní) řidiči předjeli a reportáž televize CNN byla odvysílání s velkým zpožděním. Je tedy nutno říci, že stávka programátorů neměla náležitý dopad (když ji televize CNN nestihla během týdne okomentovat) a tak budou muset brát programátoři dál obrovské sumy peněz za tak lehkou práci.
Většina řešení radila řidiči, aby si mezi dvěma stávkami vybral cestu buď přímo vodorovně nebo přímo svisle. A z těchto dvou tu, která je kratší. To je bohužel řešení chybné a dostalo nula bodů. Můžeme si to ukázat na následujícím protipříkladě:
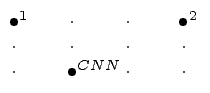
Pokud si vyberete nejkratší cestu na stávku 1, pojedete o jednu ulici doleva. Pak na stávku druhou pojedete o dvě nahoru a pak o tři zpět do CNN, čili celkem šest. Ovšem pokud byste se ovšem vydali na začátku nahoru o dvě ulice, nafilmovali byste obě stávky a stačilo by se vrátit – celkem tedy pouze 4 ulice.
Úloha se dala řešit několika způsoby. Jeden z nich je prohledávání do šířky. Představme si ne jedno, ale M měst přesně nad sebou, přičemž v prvním je jen CNN a první stávka, v druhém je jen druhá stávka, … , v M-tém městě je M-tá stávka a opět CNN. Pokud si představíme, že z města i se do (i+1)-ního dá dostat jen z ulic v městě i, ze kterých je vidět i-tá stávka, tak hledáme nejkratší cestu z CNN v prvním městě do CNN v městě M-tém. Tato nalezená cesta bude nejkratší a vzhledem k tomu, jak přecházíme mezi městy, bude u každé stávky. Toto řešení má časovou i paměťovou složitost úměrnou velikosti prohledávaného prostoru, čili O(M·N2).
Jiný pohled na řešení může být tento: pro města i od M-tého k prvnímu si spočteme matici Ci, ve které budeme mít pro každou křižovatku v daném městě nejkratší vzdálenost cesty, která nafilmuje stávky i,… ,M a vrátí se do CNN. Pokud tyto matice vzdáleností budeme počítat v popsaném pořadí od M-té k první, můžeme spočítat délku jedné nejkratší cestu (jeden prvek matice) v konstantním čase: v i-tém městě na křižovatce (x,y) vede hledaná nejkratší cesta buď horizontálně nebo vertikálně na ulici, ze které je možné nafilmovat i-tou stávku a a pak pokračuje dále (přičemž délku tohoto pokračování už známe). Čili délka této cesty (pokud i-tá stávka je na křižovatce (i,j)) je min(abs(x-i)+Ci+1(i,y),abs(y-j)+Ci+1(x,j)).
Tímto máme další řešení, které musí počítat M·N2 čísel, každé v konstantním čase. To není o nic lepší. Ale můžeme si všimnout jedné věci – hodnoty matice Ci+1, které při výpočtu skutečně použijeme, leží vždy jen na ulicích, ze kterých je vidět i-tá stávka. Takže vlastně nepotřebujeme počítat hodnoty v celé matici Ci+1, stačí pouze ty, ze kterých je vidět i-tou stávku. Těch je ale docela málo – přesněji 2N-1.
Z toho plyne následující řešení: pro každou stávku od M-té k první si spočteme délku nejkratší cesty, která nafilmuje stávky i,… ,M a skončí v CNN. Tyto délky budeme ale počítat jen ve křižovatkách, ze kterých můžeme i-tou stávku nafilmovat. K výpočtu těchto délek nám poslouží již popsaný vzoreček.
Navíc pokud si u každé křižovatky budeme pamatovat, kudy z ní nejkratší cesta vede, můžeme nakonec i vypsat cestu vozu (a popředu – proto jsme hledali nejkratší cesty od poslední stávky). Celkem má naše řešení časovou i paměťovou složitost O(M·N). Paměťová by šla snížit na O(N), ovšem jen pokud bychom nechtěli znát cestu, ale jen její délku.

 Další možnost, i když poněkud zběsilá: Jak víme, hodnoty, které potřebujeme,
leží na „kříži“ † aktuální stávky (tak budeme říkat křižovatkám,
ze kterých je tato stávka vidět) a počítáme je z hodnot na kříži †'
následující stávky. Každý kříž si ale můžeme rozdělit na svislou a vodorovnou
část. Pak hodnoty na vodorovné části † budou hodnoty z vodorovné
části †', pouze zvýšené o vzdálenost obou přímek, a navíc ještě průmět
všech hodnot ze svislé části kříže †' do průsečíku příslušné svislé přímky
s naši vodorovnou, který ohodnotíme minimem z (vzdálenost bodu od vodorovné
přímky + ohodnocení bodu). To není o mnoho lepší řešení, ale jen do okamžiku,
kdy si uvědomíme, že by se celá situace dala udržovat ve dvou vyhledávacích
stromech – jednom pro svislý směr a jednom pro vodorovný –, přičemž podobně
jako si v úloze 16-4-5 udržujeme minimální rozdíl, bychom si udržovali minimum
z (souřadnice ve směru přímky + ohodnocení bodu), a tak bychom dokázali
od jednoho kříže k druhému přejít v čase O(log N), dosahujíce tak celkové
časové složitosti O(M· log N). –M.M.
Další možnost, i když poněkud zběsilá: Jak víme, hodnoty, které potřebujeme,
leží na „kříži“ † aktuální stávky (tak budeme říkat křižovatkám,
ze kterých je tato stávka vidět) a počítáme je z hodnot na kříži †'
následující stávky. Každý kříž si ale můžeme rozdělit na svislou a vodorovnou
část. Pak hodnoty na vodorovné části † budou hodnoty z vodorovné
části †', pouze zvýšené o vzdálenost obou přímek, a navíc ještě průmět
všech hodnot ze svislé části kříže †' do průsečíku příslušné svislé přímky
s naši vodorovnou, který ohodnotíme minimem z (vzdálenost bodu od vodorovné
přímky + ohodnocení bodu). To není o mnoho lepší řešení, ale jen do okamžiku,
kdy si uvědomíme, že by se celá situace dala udržovat ve dvou vyhledávacích
stromech – jednom pro svislý směr a jednom pro vodorovný –, přičemž podobně
jako si v úloze 16-4-5 udržujeme minimální rozdíl, bychom si udržovali minimum
z (souřadnice ve směru přímky + ohodnocení bodu), a tak bychom dokázali
od jednoho kříže k druhému přejít v čase O(log N), dosahujíce tak celkové
časové složitosti O(M· log N). –M.M.
16-4-4 Dlouhoprstova zapeklitá hra (Zadání)
Většina z vás, zdá se, přála Dlouhoprstovi buďto předlouhý život nebo z pekla štěstí, jelikož většina řešení byla buďto ďábelsky pomalá (pracovala v exponenciálním nebo dokonce faktoriálovém čase) nebo to byly po čertech podivné heuristiky fungující pouze pro některé vstupy a pro jiné se chovající značně démonicky. Ale přeci jen někteří dokázali našemu hrdinovi (neříkám, že kladnému) s dlouhými prsty a krátkýma nohama pomoci. Jde to třeba takto:
Označme si D(α,β) nejkratší možnou posloupnost Dlouhoprstových karet (Dlouhoprstova posloupnost, zkráceně DP), která odpovídá Satanovým posloupnostem (SP) α a β. Podle toho, jak α a β začínají, můžeme rozlišit následující případy:
- D(xα, xβ) = xD(α,β) – pokud začínají obě SP stejným písmenem, musí DP začínat také tímto písmenem a za ním bude následovat DP pro původní SP bez tohoto písmena.
- D(xα, yβ) = Ψ – pokud SP začínají různými písmeny, evidentně příslušná DP neexistuje, takže vrátíme chybu, a tu budeme značit Ψ.
- D(ε, ε) = ε – pokud jsou obě SP prázdné, je DP také (ε budeme značit prázdný řetězec).
- D(xα,
*β) = min(D(xα, β), D(α,*β) ) – pokud se objeví hvězdička, můžeme ji buďto splnit prázdným řetězcem a nebo ji nechat „spolknout“ první písmenko druhého řetězce (případně i nějaká další, protože*v řetězci ponecháme). Vybereme si samozřejmě kratší z obou variant (jako min značíme minimum řetězcové, které z dvou řetězců vrátí ten kratší a pokud mají stejnou délku, tak libovolný z nich; navíc Ψ je delší než všechny řetězce). - D(ε,
*β) = D(ε, β) – pokud je levá strana prázdná, musí hvězdičce vyhovovat prázdný řetězec, ale ještě musíme pokračovat, protože napravo může být hvězdiček více. - D(
*α, xβ), D(*α, ε) – analogicky. - D(
*α,*β) = min(D(α,*β), D(*α, β) ) – pokud obě SP začínají na*, nemá smysl do DP přidávat znaky, které by měly vyhovovat oběma hvězdičkám – ty by byly zbytečné. Takže chceme jednu z hvězdiček vypustit a druhou ponechat, jen si musíme vybrat tu správnou, pročež zkusíme obě. - pokud se někde vyskytne otazník, můžeme ho chápat jako písmeno, které se rovná libovolnému jinému písmenu a pokud bychom ho chtěli vypsat do výstupu, vypíšeme místo něj libovolné jedno písmeno.
- D(xα, ε) a ostatní zbylé případy (jedna SP došla a druhá ještě ne) jsou neřešitelné, a tak odpovíme Ψ.
Rekursivním použitím těchto pravidel už můžeme spočítat D pro libovolnou dvojici Satanových posloupností, ale má to jeden háček: rekurse se nám na hvězdičkách větví, takže může trvat exponenciálně dlouho. Jak z toho ven?
Všimneme si, že všechny řetězce, pro které D počítáme, jsou vždy suffixy původních SP (suffix je část řetězce od nějakého místa až do konce) a rekurse je exponenciální jen proto, že se pro mnohé dvojice suffixů počítá totéž vícekrát. Budeme si proto již spočtené hodnoty pamatovat v pomocném poli a kdykoliv by po nás někdo chtěl hodnotu spočítat znovu, prostě ji jen vytáhneme z pole jako králíka z klobouku a hned se vrátíme bez dalšího rekursivního volání. Možných dvojic suffixů je jenom (M+1)·(N+1), takže netriviálních volání funkce D může být jen O(M·N).
Již z toho by plynul pěkný algoritmus se složitostí (M·N·(M+N)), ale ten by většinu času trávil předáváním řetězců mezi funkcemi. Tak se ho ještě zkusíme zbavit: Všimneme si, že každé D(α,β) vždy získáme z nějakého D(α′, β′) (kde α′ je nějaký suffix řetězce α a obdobně β′) přidáním jednoho nebo žádného znaku na začátek. Naše funkce tedy místo toho, aby vrátila řetězec, jen poznamená do nějakého pomocného pole, jak má hodnota vzniknout a jak bude dlouhá (to zvládneme na konstantní počet operací), a po ukončení výpočtu ten správný řetězec podle těchto poznámek zrekonstruujeme (v lineárním čase).
Celkově má tedy náš algoritmus časovou i paměťovou složitost O(M·N).
16-4-5 Obchodníci s deštěm (Zadání)
Velkou část našich řešitelů O. Š .Kubal, věren svému jménu, žel Bůhdhovi, o.š.kubal. Svými pomalými programy totiž nedokázali zjistit, jaký zmetek jim chtějí Kubalovi prodat.
První věci, které si všimneme, je to, že čas potřebný na jednu odpověď (vypsání aktuálního rozdílu po přečtení jednoho čísla) by neměl být závislý na N, ale jenom na K.
Nejjednodušší řešení je, po načtení další hodnoty, spočítat všechny vzdálenosti dvojic posledních K vrcholů a z nich si vybrat tu nejmenší. To určitě zvládneme v O(N·K2).
Vylepšit to můžeme například tak, že si všimneme, že pokud bychom měli posledních K hodnot setříděných, nemusíme zkoumat O(K2) vzdáleností, stačí nám spočítat vzdálenosti mezi dvěma sousedními prvky (sousedí v setříděném poli). Těch už je jenom K-1, nicméně třídění nás stojí zase O(K log K). Celkem vylepšení na O(N·K log K).
Další pozorování je, že po načtení jednoho čísla se pole posledních K čísel moc nezmění – určitě nemá cenu ho třídit vždy znova. Pokud máme setříděné pole posledních K čísel a načítáme další, stačí to nejstarší z pole vyhodit (O(K)) a nové přidat (O(K)) tak, aby pole zůstalo uspořádané. Pak stačí v jednom průchodu nad polem spočítat vzdálenosti sousedních prvků a vypsat nejmenší. Tím jsme na O(N·K).
Vylepšovat ale jde dále. Ukážeme si dvě možná řešení se složitostí O(N· log K). První z nich je založeno na tomto pozorování: pokud uvažujeme o postupu s lineárním časem, tak počet dvojic, jejichž vzdálenost počítáme, se při načtení jednoho čísla mění velmi málo. Můžeme tedy mít všechny vzdálenosti sousedních prvků (sousedních v setříděném poli) v haldě. Při načtení nového čísla ho zatřídíme do nějaké struktury (použijeme např. AVL stromy z minulé kuchařky), která nám řekne jeho sousedy (většího a menšího) v setříděném poli. Pokud už je máme, z haldy odebereme vzdálenost těchto dvou sousedů a naopak do ní vložíme vzdálenost aktuálního prvku od menšího a vzdálenost aktuálního prvku od většího souseda. Při mazání čísla uděláme podobnou úpravu (zase si najdeme sousedy mazaného prvku, z haldy odebereme dvě hodnoty a dáme tam místo nich jednu [vzdálenost sousedů mazaného prvku]).
Pokud použijeme ke zjišťování sousedů nějaký druh vyvážených stromů (třeba AVL :–), můžeme hledání sousedů, vkládání a mazání provádět v čase O(log K). Stejnou složitost mají i operace s haldou – a protože všeho tohoto děláme konstantní počet, máme řešení se složitostí O(N· log K).
To bylo jedno řešení, slíbili jsme ještě druhé: opět použijeme nějaký vyvážený binární strom. Každý jeho vrchol bude odpovídat jednomu z posledních K čísel, nicméně ve vrcholu si kromě hodnoty budeme pamatovat ještě tyto údaje:
- min – minimum hodnot v tomto podstromě.
- max – maximum hodnot v tomto podstromě.
- delta – nejmenší vzdálenost hodnot v tomto podstromě.
Pokud máme vrchol a známe tyto hodnoty u obou jeho synů, můžeme si spočítat i jeho hodnoty v konstantním čase:
- min – vezmeme minimum od levého syna.
- max – vezmeme maximum od pravého syna.
- delta – vezmeme minimum z delt levého a pravého syna, dále ze vzdálenosti hodnoty aktuálního vrcholu od maxima levého syna a ještě rozdíl hodnoty aktuálního vrcholu a minima pravého syna.
Můžeme tedy načtené hodnoty vložit do stromu, přepočítat popsané hodnoty a vypsat deltu kořene. Přepočítání hodnot můžeme provádět tak, že po vložení/smazání prvku budeme stromem procházet od vloženého/smazaného prvku směrem ke kořeni a po cestě upravovat popsané hodnoty. Pokud bude strom opravdu vyvážený, bude mít logaritmickou hloubku a tedy popsané operace budou mít složitost O(log K) a celé řešení tedy O(N· log K).
Ve vzorovém řešení jsme schválně nepoužili AVL stromy, ty už znáte. Použili jsme tzv. BB-α stromy, které mají logaritmickou složitost pouze amortizovaně. To nám ale vůbec nevadí, protože nás zajímá složitost N operací a ne jedné.
 BB-α strom je normální binární vyhledávací strom takový, že v každém vrcholu
platí podmínka, že počet vrcholů v levém a pravém podstromě se liší nanejvíc
α-krát. Takový strom má vždy logaritmickou hloubku, protože podstrom nějakého
stromu má nanejvýš α/(α+1) vrcholů – počet vrcholů v podstromu tak klesá
geometrickou řadou a maximální možná výška stromu je tak log(α+1)/αN.
BB-α strom je normální binární vyhledávací strom takový, že v každém vrcholu
platí podmínka, že počet vrcholů v levém a pravém podstromě se liší nanejvíc
α-krát. Takový strom má vždy logaritmickou hloubku, protože podstrom nějakého
stromu má nanejvýš α/(α+1) vrcholů – počet vrcholů v podstromu tak klesá
geometrickou řadou a maximální možná výška stromu je tak log(α+1)/αN.
A jak takovou podmínku dodržet? U každého vrcholu si budeme udržovat počet vrcholů v levém a pravém podstromu. Pokud kdykoliv zjistíme, že se liší více než α-krát, celý podstrom odpojíme, vytvoříme z něj vyvážený strom a vrátíme zpátky. Takové „vybalancování“ určitě trvá lineárně vzhledem k počtu vrcholů ve vybalancovávaném stromečku.
Předpokládejme nyní, že α=2, stejně jako ve vzorovém programu. Kolik stojí jedno vkládání či mazání? Na to, aby se nějaké vybalancování spustilo, se musí lišit hodnoty v levém a pravém podstromu dvakrát, čili od minulého rebalancování muselo dojít k řádově tolika vkládáním a mazáním, kolik je vrcholů ve zkoumaném stromečku. Čili stačilo, aby každé vkládání a mazání přispělo aktuálnímu vrcholu konstantním časem (jedním penízkem), ze kterého se pak vybalancování „uplatí“. Každé vkládání a mazání musí přispět na rebalancování všem vrcholům, přes které projde. Těch je ale nanejvíc tolik, jaká je výška stromu – a ta je logaritmická. Čili amortizovaná složitost vkládání nebo mazání prvku je O(log K) (amortizovaná znamená, že i když nevíme, jak dlouho bude jedna operace doopravdy trvat, N operací bude trvat nejvýš O(N·K)).
16-4-6 Šikmá věž v Kocourkově (Zadání)
Řešení potíží našich věžechtivých Kocourkovanů v kostce: Klíčové úkony leží na nejdelší cestě v závislostním grafu (acyklickém!) a všechny takové cesty můžeme najít projitím grafu v topologickém pořadí.
Připusťme ale poněkud pomalejší chápání kocourkovských buřtipánů a zkusme tento nápad poněkud rozvést:
Nejdříve si sestrojíme závislostní graf: to bude orientovaný graf, jehož vrcholy budou odpovídat úkonům a z u do v povede hrana právě tehdy, když je nutné úkon u dokončit před započetím úkonu v; navíc si každý vrchol ohodnotíme číslem, které bude udávat, jak dlouho příslušný úkon trvá. Ještě přidáme počáteční úkon α odpovídající položení základního kamene stavby (ohodnocena nulou a vedou z ní hrany do všech ostatních úkonů) a úkon ω odpovídající kolaudaci (opět nula [naivní, vím], hrany ze všech ostatních úkonů). Délkou cesty budeme nazývat součet ohodnocení vrcholů, které na ni leží, bez počátečního a koncového vrcholu, což je sice trochu nesystematické, ale usnadní nám to počítání. Odlehlostí z vrcholu (úkonu) u do v pak nazveme délku nejdelší cesty z u do v (to je svým způsobem opak vzdálenosti, která je délkou cesty nejkratší).
Pokud je v závislostním grafu cyklus, věž evidentně postavit nelze. Budeme tedy předpokládat, že graf je acyklický a ukážeme, že věž postavit půjde, a to v čase rovném odlehlosti L z α do ω. Ještě trocha značení: pro každý úkon u bude l(u) délka tohoto úkonu, a(u) odlehlost z α do u a z(u) odlehlost z u do ω.
Teď ale na chvíli odbočíme od tématu a zavedeme si topologické pořadí vrcholů grafu. Tak budeme říkat takovému pořadí v1,v2,…,vn všech vrcholů, pro které platí, že pokud vede hrana z vi do vj, je vždy i<j. V libovolném acyklickém grafu takové pořadí existuje, což si dokážeme tak, že si rovnou předvedeme lineární algoritmus, který ho najde.
Pokud je graf acyklický, musí v něm existovat vrchol v1, kam nevede žádná hrana: stačí vyjít z libovolného vrcholu a stále jít proti směru hran – jelikož graf je konečný, nemůžeme přicházet do stále nových vrcholů, takže časem narazíme buďto na vrchol, do kterého nic nevede, nebo na vrchol, ve kterém jsme už byli, což ovšem není možné, protože bychom tím uzavřeli cyklus. Nalezený vrchol v1 očíslujeme jedničkou (to je určitě správně, nevede do něj přeci žádná hrana) a z grafu ho odebereme včetně všech hran, které z něj vedou. Tím získáme opět acyklický graf a v něm pokračujeme stejně od dvojky. Až nezbude žádný vrchol, budeme mít hotové topologické pořadí; pokud by nějaký zbyl, znamená to, že se v grafu nacházely cykly. Abychom ale dosáhli lineární časové složitosti, potřebujeme umět takové vrcholy nacházet v konstantním čase. K tomu stačí zapamatovat si pro každý vrchol počet hran, které do něj vedou, při odebírání hran tyto počty aktualizovat a udržovat si frontu vrcholů, které už mají nulu, ale ještě jsme je neodebrali.
[Ve vzorovém programu nepřiřazujeme čísla explicitně, ale využíváme toho, že ve frontě jsou vrcholy uloženy také v topologickém pořadí. Ještě jiný způsob, jak topologické pořadí najít, by byl prohledat graf do hloubky a všimnout si, že pořadí, ve kterém se z vrcholů vracíme, je obrácené topologické pořadí. Zkuste si rozmyslet, proč to platí, v některé z kuchařek v příštím ročníku se na to podíváme podrobněji.]
Hodnoty a(u) pak můžeme spočítat velice snadno indukcí: bereme vrcholy v topologickém pořadí, začínáme s a(α)=0. Pro každý další vrchol využijeme toho, že již známe a(v) pro všechny předchůdce v vrcholu u, čili vrcholy, z nichž vede do u hrana, a položíme a(u)=maxv (a(v) + l(v)) (nejdelší cesta z α do u musí být nutně nejdelší cestou do některého z předchůdců u prodloužená o hranu do u). To zvládneme v lineárním čase a stejně tak můžeme spočítat i b(u) pomocí opačného topologického pořadí a L jako a(ω) nebo z(α).
(Konec odbočky.) Nyní si všimněme, že žádný úkon nelze začít provádět dříve než v čase a(u): víme totiž, že existuje posloupnost úkonů, které musí být všechny provedeny po sobě a před u a dohromady trvají a(u). Z toho také plyne, že celou věž nemůžeme dostavět dříve než za L=a(ω). Teď už stačí ukázat, že si můžeme úkony rozvrhnout tak, abychom u dokončili v čase a(u)+l(u), a tedy celou stavbu v čase L. To je snadné: každý úkon u začneme provádět v čase a(u) a vzorec pro a(u) z minulého odstavce vlastně říká přesně to, že všechny předchozí úkoly jsou nejpozději v tomto okamžiku hotové.
Zbývá ještě zjistit, které úkoly jsou klíčové: jsou to ty, které leží na některé z nejdelších cest (tedy ty, pro které je Lu=L, kde Lu=a(u)+b(u)+l(u) je délka nejdelší cesty z α do ω, která obsahuje u). Pokud úkon u na nejdelší cestě leží, je nutně klíčový, protože na úkonech na nejdelší cestě pracujeme po celou dobu L bez přestávek, takže pokud libovolný úkon prodloužíme, prodloužíme i celou dobu stavby. Naopak pokud úkon u neleží na nejdelší cestě, můžeme ho prodloužit až o L-Lu a celkovou dobu tím nezměníme.
Program je toliko formálním zápisem našich úvah a má lineární časovou složitost a kvadratickou paměťovou (ale jen proto, že jsme si ušetřili práci s načitáním hran; jinak by byla také lineární).
[Všchn thle b s smzřjm dlo smrsknt d jdnh prchdu grfm, le bl b t čtlné as jko thl vta. –M.M.]