První série šestnáctého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Zadání úloh

16-1-1 Telefonní seznam (5 bodů)

Vytrvalejším řešitelům našeho semináře již dobře známá společnost Shumm & Brumm rozšiřuje své podnikání v oblasti telekomunikací a jejím nejnovějším počinem má být všeobsahující telefonní seznam. Oddělení pro shromažďování údajů již získalo všechna jména a telefonní čísla a předalo je Oddělení pro třídění údajů, které začalo jména třídit. Třídění je nicméně práce značně vyčerpávající a pracovníci oddělení si to postupně srovnávali v hlavě a odcházeli za lepším výdělkem. A tak se jednoho dne stalo, že nezbyl nikdo, kdo by třídil. Vedení společnosti se v zoufalství obrátilo na vás, abyste pomohli dotřídit onen seznam.

Vaším úkolem je navrhnout algoritmus a napsat program, který dostane na vstupu počet jmen v seznamu N a dále předtříděný seznam jmen (háčky a čárky ve jménech či českou specialitu s tříděním „ch“ nebudeme uvažovat). Seznam je předtříděný tak, že libovolné jméno se v něm nachází nejvýše ve vzdálenosti k od místa, kde bude v setříděném seznamu. Toto číslo k též dostane váš program na vstupu. Na výstup má váš program vypsat setříděný seznam jmen.

Příklad: Pro seznam sedmi jmen Pycha, Kopyto, Pytel, Netopyr, Pysk, Spytihnev, Slepys je setříděný seznam Kopyto, Netopyr, Pycha, Pysk, Pytel, Slepys, Spytihnev. Jako k by mohl váš program dostat 2, protože nejvzdálenější od svých správných pozic byla slova Netopyr, Pycha a Pytel a ta se posunula o dvě místa.

Řešení

16-1-2 Lokální minimum (6 bodů)

Mějme pole A s N celými čísly. Řekneme, že na pozici i je lokální minimum pokud A[i-1]≥ A[i]≤ A[i+1] (pro jednoduchost předpokládáme, že A[0]=A[N+1]=∞). Vaším úkolem v této úloze nebude nic těžšího, než nalézt v daném poli pozici libovolného lokálního minima. Problém ale spočívá v tom, že byste to měli udělat skutečně rychle – asymptotická časová složitost vašeho algoritmu (nepočítáme načítání pole) by měla být menší než O(N).

Příklad: V poli 1,3,2,1,4,2,5 se lokální minima nachází na pozicích 1, 4 a 6 a váš program tedy může vrátit libovolnou z těchto pozic.

Řešení

16-1-3 Důl (7 bodů)

Těžařská společnost Coppermine získala povolení k těžbě mědi v Kaputánii. Patřičný geologický průzkum již byl proveden, stroje nakoupeny, jediný problém, který ještě zbývá vyřešit, je doprava vytěžené měděné rudy ke zpracování. Společnost sice disponuje velkými nákladními auty, nicméně silnice v Kaputánii jsou poměrně nízké kvality a plně naložené nákladní auto by nemusely unést. Plánovače společnosti Coppermine by přirozeně zajímalo, jaké nejtěžší auto může projet z dolu do továrny na zpracování rudy, a proto se obrátili na vás.

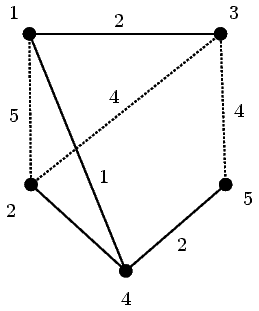
Vaším úkolem je navrhnout algoritmus a napsat program, který dostane na vstupu počet měst v Kaputánii N, počet silnic M a dále popis oněch silnic. Každá silnice vede mezi dvěma městy a předpokládáme, že mimo města se silnice nekříží. Silnici proto popisují jednoznačně čísla dvou měst (města si očíslujeme od jedné do N), mezi kterými vede. Dále je u každé silnice udána její nosnost. Na výstup má váš program vypsat cestu z dolu do továrny (důl je ve městě s číslem 1 a továrna ve městě s číslem N), po které může projet co nejtěžší auto – mezi všemi cestami z dolu do továrny to je taková cesta, na které je minimum z nosností jednotlivých úseků co největší. Můžete předpokládat, že mezi dolem a továrnou vždy vede nějaká cesta. Pokud je cest se stejnou nosností více, můžete vrátit libovolnou z nich.

Příklad: Pro situaci jako na obrázku by měl váš program nalézt cestu 1,2,3,5, po které může projet auto s váhou 4.

Graf cest

Řešení

16-1-4 Neruš mé trojúhelníky! (8 bodů)

V průběhu věků lidé vymysleli mnoho různých více či méně šílených šifrovacích metod. Jednu z nich vymysleli kryptografičtí odborníci z Artustánu. Zašifrovaná zpráva vypadala jako několik nevinně vyhlížejících kružnic s vyznačenými některými body na obvodu. Výzvědná služba ze sousedního Bosstánu dlouho nemohla šifru rozluštit, až se jednomu z jejích špiónů podařilo vypátrat, že pro šifru je podstatný počet trojúhelníků s vrcholy ve vyznačených bodech, které obsahují střed kružnice. Zjistit toto číslo ručně je ovšem pracné, a tak jste byli požádáni o pomoc.

Vaším úkolem je navrhnout algoritmus a napsat program, který dostane na vstupu počet vyznačených bodů na obvodu kružnice N a dále N reálných čísel udávajících úhly, pod kterými jednotlivé body leží (0° je bod „na sever“ od středu, úhel roste proti směru hodinových ručiček). Na výstup pak vypíše počet trojúhelníků s vrcholy v zadaných bodech, které obsahují střed kružnice.

Obrázek kružnice

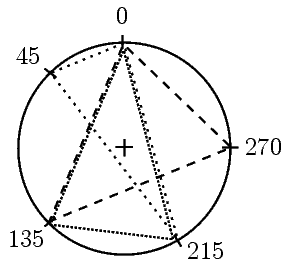
Příklad: Pro kružnici s pěti vyznačenými body na pozicích 0°,45°,135°,215°,270° (viz obrázek) existuje pět trojúhelníků obsahujících střed.

Řešení

16-1-5 Pravděpodobnostní algoritmy (9 bodů)

V letošním ročníku jsme se rozhodli, že v rámci obvyklého seriálu uvedeme několik úloh zaměřených na pravděpodobnostní algoritmy. Co to takový pravděpodobnostní algoritmus je? Inu je to vlastně obyčejný algoritmus, který ale navíc při svém běhu využívá náhodná čísla. Asi si řeknete: „K čemu nám jsou náhodná čísla dobrá?“ Ač to je možná na první pohled překvapivé, náhodná čísla mohou pomoci výrazně urychlit běh našeho algoritmu.

Protože náhodná čísla se budou táhnout celým naším seriálem, měli bychom si nejdříve ujasnit, co si pod tímto pojmem představujeme. Obvykle budeme potřebovat generovat náhodná celá čísla z nějakého intervalu 0… N-1 tak, aby všechna čísla měla stejnou pravděpodobnost (tedy abychom každé číslo vygenerovali s pravděpodobností 1/N). Získat takové náhodné číslo ale není tak jednoduché, jak by se mohlo zdát a my toho využijeme v naší první úloze.

Představte si, že máte k dispozici generátor náhodných bitů – tedy nějakou funkci randbit, která vám s pravděpodobností 1/2 vrátí 0 a s pravděpodobností 1/2 vrátí 1 – a chcete s její pomocí vytvořit funkci random(N), která vrací náhodné číslo z intervalu 0… N-1 (takové, jaké jsme popsali v předchozím odstavci). Navíc bychom chtěli, aby vaše funkce random potřebovala na vygenerování jednoho náhodného čísla co nejméně volání funkce randbit. Součástí vašeho řešení by mělo být jednak zdůvodnění, proč váš generátor vygeneruje každé číslo z daného intervalu se stejnou pravděpodobností a jednak odhad počtu volání funkce randbit.

Řešení