Třetí série devatenáctého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

• 19-3-1: Jezírka
• 19-3-2: Inventura ve spíži
• 19-3-3: Nevěrné ženy
• 19-3-4: Nejbližší rostoucí posloupnost
• 19-3-5: Pevné vztahy
• 19-3-6: Prolog

19-3-1 Jezírka (Zadání)

Sice se proslýchá, že lesní duchové umí tuto úlohu řešit ještě rychleji (a to v O(log N), nám smrtelníkům bude stačit řešení lineární v čase i paměti. Jak tedy na to?

Napřed si všimněme, že ve struktuře jezírek nejsou cykly. Kdyby tam nějaký byl, dá se z něj některá hrana odebrat a tím cenu snížit. Dále si všimněme, že jednou odmítnutá cesta se již nikdy nepoužije (jednak by ji museli bobři zrekonstruovat, jednak je delší než něco co tam je místo ní).

Nyní za námi přijde předák kanců a nahlásí nám cestu mezi jezírky J a K dlouhou d. Co se může stát? Buď spojuje oblasti, mezi kterými zatím bobři běhali po souši, a v takovém případě ji s radostí přijmou, čímž celkovou délku cest zvýší o d. Druhým případem je, když se i předtím dalo z J do K dostat. Nyní tedy jsou 2 cesty mezi nimi, což je zbytečné a jednu lze nechat chátrat (samozřejmě tu nejdelší) a upravit aktuální celkovou délku (snížit o rozdíl nejdelší a nové).

Nyní, jak tedy rozhodnout? Mezi prvním a druhým případem by se dalo rozlišit pomocí DFU z kuchařky, ale protože si tím stejně časovou složitost nevylepšíme, je to zbytečná práce. Tak tedy rovnou zkusíme najít cestu z J do K. Protože nemáme cykly, existuje nejvýše jedna. Pokud taková cesta neexistuje, tak se jedná o první případ a hranu přidáme. Když cestu najdeme, tak vezmeme její nejdelší hranu (kterou můžeme zjistit při hledání) a porovnáme s novou, v případě že se nám to hodí, je vyměníme.

Nalezení cesty můžeme provést kupříkladu prohledáním do hloubky (je jednodušší na napsání).

Protože graf nemá kružnice, je to les. A les může mít maximálně N-1 hran a v takovém případě je souvislý (tedy je to strom). Počítání hran lze využít k určení, jestli už jsou všechna jezírka propojená.

Protože si stačí pamatovat jen aktuální cesty, tak nám stačí paměť lineární s počtem jezírek. Stejně tak, při průchodu do hloubky se každá hrana a každé jezírko navštíví nejvýše jednou a tedy i časová složitost je lineární. Pokud si vybereme správnou reprezentaci v paměti. (Ve vzorovém programu je použit spojový seznam sousedů v každém vrcholu).

Program

Michal "vorner" Vaner

19-3-2 Inventura ve spíži (Zadání)

Ač řešení této úlohy přišlo mnoho, bylo je možné rozdělit do pouhých tří skupin. Nejprostším řešením bylo pro každou ještě nezpracovanou potravinu projít všechny zbývající potraviny a počítat kolikrát se mezi nimi vyskytla. Časová složitost O(N²) však byla příliš vysokou daní jednoduchosti.

Druhá skupina si potraviny seřadila podle velikosti některým z rychlých třídících algoritmů a pak jedním průchodem vypsala hledané potraviny. Časová složitost se tak zlepšila na O(N log N).

A konečně poslední skupina použila hashování, s jehož pomocí získáme v průměrném případě lineární časovou složitost.

My si ukážeme řešení, které je rovněž lineární k délce vstupu, ale na rozdíl od hashování i v nejhorším případě a navíc není omezené předpokladem, že se nám čísla potravin vejdou do proměnné. Řešení využívá triviálního pozorování - desítkové číslo je posloupnost znaků 0-9. A vhodnou datovou strukturou pro vyhledávání posloupností znaků (neboli řetězců) jsou trie (nebo také slovníkové/prefixové stromy).

Trie je vícecestný strom, z jehož libovolného uzlu může vést až N hran. Oproti obyčejným vyhledávacím stromům, kde každá hrana odpovídá nějakému intervalu, si můžeme u trií dovolit (díky omezené abecedě) odkazovat se na hranu přímo pomocí znaků použité abecedy.

Přidání slova do trie je pak jednoduché. Postupně beru znaky slova a jdu v trii od kořene po hranách příslušných aktuálnímu znaku nebo, pokud takové hrany neexistují, tak je vytvářím.

Zjevně pak platí, že posloupnost hran z kořene do libovolného uzlu odpovídá předponě nějakého slova, které je v trii uloženo, což nám umožňuje jednoduše všechna slova z trie vypsat.

Pokud tedy v tomto případě zvolíme za N číslo 10, tj. počet desítkových číslic, a jako slova slovníku použijeme čísla potravin, můžeme v čase lineárním vzhledem k délce čísla potraviny zjistit, jestli se taková již vyskytla, resp. ji můžeme v lineárním čase do trie přidat. Abychom mohli počítat, kolikrát se jednotlivé potraviny ve spíži vyskytují, přidáme si do každého uzlu proměnnou, ve které si budeme pamatovat, kolik čísel potravin v tomto uzlu končí.

Hledané potraviny nakonec najdeme jednoduchým průchodem trií do hloubky. Časová složitost celého algoritmu je O(N), paměťová je rovněž O(N).

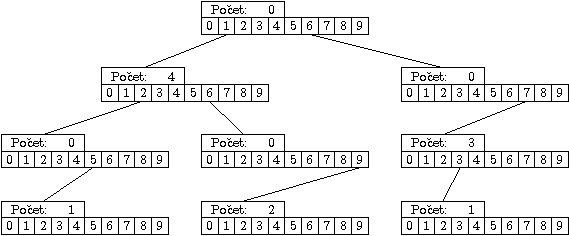
Pro lepší představu, jak takové trie vypadají, se můžete podívat na obrázek, kde je zachycená pro vstup 1, 125, 1, 169, 67, 1, 67, 673, 169, 67, 1.

Program

Zbyněk Falt

19-3-3 Nevěrné ženy (Zadání)

Většina z vás vyřešila tuto úlohu perfektně. Pokud nemáte plný počet bodů, bylo to zřejmě proto, že jste dostatečně neodůvodnili vaše řešení. Nebylo důležité napsat formální důkaz správnosti, ale rozumně vysvětlit, proč je vaše řešení správné. Důležitý byl zejména zobecňující krok, kterým jste ukázali, že vaše tvrzení platí pro obecně k manželek. Tzn. nestačilo pouze říci, že když to platí pro čísla 1, 2 a 3, tak to určitě platí i pro k. Nebudu vás déle napínat a ukážu vám, jak mělo řešení vypadat.

Budeme krůček po krůčku rozebírat možnosti, kolik mohlo být nevěrných žen, až se dostaneme ke kýženému číslu. Nultého dne se na večírku dozvídáme (patrně pravdivou informaci), že alespoň jedna žena je nevěrná. Tak se zamysleme, jak by vypadalo chování mafiánů, kdyby byla právě jedna žena nevěrná. Všichni mafiáni, až na jejího manžela, by věděli, která to je. Manžel této ženy by nevěděl o žádné jiné nevěrné ženě (všechny ostatní jsou věrné), a tak by mu došlo, že nevěrná musí být jeho žena. Tím pádem by ji zabil hned následujícího dne (tzn. k vraždě by došlo již první den).

Zkusme se podívat o krok dál – kdyby byly právě dvě ženy nevěrné. Manželé obou žen (označme je A, B) jsou první den v klidu. Oba totiž znají jednu ženu, která podvádí manžela (A ví nevěře manželky B a naopak). Jenže když A zjistí, že první den B svoji ženu nezabil, dojde mu, že B zná ještě jednu nevěrnici a protože A zná jen jednu, je jasné, že to musí být jeho žena. Oba tedy zabijí své manželky druhý den.

Analogicky můžeme tento postup iterovat. Obecně můžeme říci, že pokud je právě k žen nevěrných, dovtípí se to jejich manželé právě za k dní. Každý podváděný manžel ví o k-1 jiných nevěrnicích, a tak teprve když se k-1 dne dozví, že ženy jsou stále naživu, nezbývá jiná možnost, než že nevěrnic je o jednu víc (a ta jedna nemůže být žádná jiná, než jeho žena).

Nebylo to zase tak těžké, ne? Ale kdyby se i přesto našel někdo, kdo se do předchozího vysvětlení zamotal, nechť se ozve na diskusním fóru a já se pokusím ho rozmotat.

A rada na závěr: Nepodvádějte (ať jste jakéhokoli pohlaví) a když už musíte, dejte si pozor na mafiány!

Martin "Bobřík" Kruliš

19-3-4 Nejbližší rostoucí posloupnost (Zadání)

„Posloupnost čísel? Ty se přeci řeší pomocí dynamiky.“ Zdá se, že dynamické programování by měl být ten správný prostředek na vyřešení této úlohy. Když se ale na problém podíváme ze správného úhlu, zjistíme, že ho dokážeme vyřešit ještě rychleji. Popíši zde řešení, které nám přišlo od Marka Nečady.

Nejprve si zadání trochu upravíme. Od i-tého prvku vstupní posloupnosti odečteme i. Nyní hledáme nejbližší posloupnost k takto upravené posloupnosti, která je neklesající. Dva sousední prvky se tedy již mohou rovnat.

Speciální posloupností je nerostoucí posloupnost, kde je každý prvek menší nebo roven předchozímu. Všimněme si, že nejbližší neklesající posloupnost k nerostoucí posloupnosti je konstantní posloupnost. Všechny prvky konstantní posloupnosti se rovnají jednomu číslu, které bude v případě nejbližší konstantní posloupnosti medián posloupnosti (medián je takové číslo m posloupnosti, že maximálně polovina čísel posloupnosti je ostře větší než m a maximálně polovina čísel je ostře menší než m). Proč je to právě medián?

Ukážeme, že nejbližší konstantní posloupnost k libovolné posloupnosti je složena z mediánu posloupnosti. Nechť je nejbližší konstantní posloupnost složena z čísel a. Rozdělme si posloupnost na čísla větší než a, rovna a a menší než a. Jejich počty označme po řadě a₊, a₌ a a_-. Označme Δ_a vzdálenost této posloupnosti od upravené posloupnosti. Pokud je a₊ větší než polovina délky posloupnosti, pak konstantní posloupnost složena z čísel a + 1 má vzdálenost Δ_a+1 = Δ_a - a₊ + a₌ + a_- < Δ_a. Podobně, pokud a_- je větší než polovina délky posloupnosti, pak konstantní posloupnost složena z čísel a-1 má menší vzdálenost. Proto a₊ a a_- jsou menší nebo rovny polovině délky posloupnosti a tedy a je medián.

To nás vede k definici tzv. mediální posloupnosti. Mediální posloupnost je taková posloupnost, že k ní nejbližší neklesající posloupnost je konstantní posloupnost rovna jejímu mediánu. Již jsme ukázali, že nerostoucí posloupnost je mediální. Naším cílem je ukázat, že posloupnost skládající se ze dvou po sobě jdoucích mediálních posloupností je také mediální posloupnost, pokud medián první posloupnosti je větší nebo roven mediánu druhé posloupnosti.

Bude následovat ošklivý technický důkaz. Nejprve dokažme pomocné tvrzení: Posloupnost je mediální právě tehdy když každý její prefix (souvislá podposloupnost obsahující první prvek), resp. sufix (souvislá podposloupnost obsahující poslední prvek), má medián větší nebo roven, resp. menší nebo roven, mediánu celkové posloupnosti.

Nejprve dokažme implikaci zleva doprava. Pokud by některý prefix měl medián menší než je medián posloupnosti, pak vytvoříme bližší posloupnost tak, že prefix nahradíme konstantní posloupností rovnou mediánu prefixu a zbytek posloupnosti bude konstantní posloupnost rovna mediánu celkové posloupnosti. Posloupnost tedy není mediální, což je spor. Podobně bychom postupovali pro sufix. Ještě ukážeme implikaci zprava doleva. Mějme libovolnou nejbližší neklesající posloupnost, která není rovna konstantní posloupnosti rovnou mediánu. Pak určitě existuje maximální konstantní prefix menší než medián nebo maximální konstantní sufix větší než medián. V obou případech můžeme tento prefix, resp. sufix, zvětšit, resp. zmenšit, o jedna a dostat tak bližší posloupnost. Tím je tvrzení dokázáno.

Mějme dvě po sobě jdoucí mediální posloupnosti s mediány m₁ ≥ m₂. Všimněme si, že potom pro medián m celkové posloupnosti platí m₁ ≥ m ≥ m₂. Vezměme libovolný prefix celkové posloupnosti. Pokud obsahuje pouze prvky z první posloupnosti, pak má prefix medián větší nebo roven m₁ a tedy i větší nebo roven m. Nechť prefix obsahuje celou první posloupnost a část druhé posloupnosti a pro spor předpokládejme, že má tento prefix medián k menší než m. Pak ale i část prefixu zasahující do druhé posloupnosti má medián menší nebo roven k a zároveň, protože je druhá posloupnost mediální, větší nebo roven m₂. Sufix druhé posloupnosti daný jako doplněk prefixu má medián menší nebo roven m₂. Medián celkové posloupnosti je menší nebo roven k, které je menší než m, a to je spor.

Po dlouhé odbočce se vraťme zpět k algoritmu. Ten bude nyní přímočarý. Rozdělme si upravenou posloupnost na souvislé nerostoucí podposloupnosti. Nyní máme posloupnost složenou z mediálních podposloupností. Potřebujeme rychle zjistit medián mediální posloupnosti a medián spojení dvou mediálních posloupností. Protože mediální posloupnost nahradíme vždy konstantní posloupností, nepotřebujeme si pamatovat pořadí jednotlivých prvků a můžeme si je setřídit podle velikosti. Tak dokážeme rychle najít medián a spojení dvou mediálních podposloupností přechází na slití dvou setříděných posloupností, což dokážeme v čase lineárním s délkou podposloupností. Algoritmus tedy vezme dvě po sobě jdoucí mediální posloupnosti, kde první má medián větší nebo roven mediánu druhé posloupnosti, a tyto dvě posloupnosti sloučí do jedné. Protože je posloupnost konečná algoritmus skončí a dostaneme posloupnost mediálních podposloupností s rostoucími mediány. Každou z nich nahradíme nejbližší konstantní posloupností a provedeme zpětný převod na ostře rostoucí posloupnost.

Každým spojením se nám sníží počet mediálních podposloupností o jedna. Na začátku jich je maximálně n, kde n je délka vstupní posloupnosti. Každé spojení je slití dvou setříděných posloupností, které trvá O(n) a proto celková časová složitost je O(n²). Paměťová složitost je O(n).

Program

Petr Škoda

19-3-5 Pevné vztahy (Zadání)

Ačkoli se v zadání slovo graf nevyskytovalo, úloha byla, jak mnozí správně poznamenali, v podstatě grafová. Mafiáni představovali vrcholy a vztahy mezi nimi byly hrany grafu. Cílem bylo ověřovat, zda zadané vrcholy (známí určitého mafiána) tvoří úplný indukovaný podgraf, neboli kliku, ve stávajícím grafu mafie.

Toto pozorování ovšem při řešení úlohy nebylo důležité, a proto se neděste, neznáte-li některé výše uvedené pojmy a bez obav čtěte dál, už je nebudu používat.

Úloha měla svůdně jednoduché řešení, na které přišla většina z vás. Stačilo načítat vztahy například do "matice známostí" (v grafové terminologii zvané matice sousednosti). Je to tabulka (tedy dvourozměrné pole), která má v i-tém řádku a j-tém sloupci 1, pokud se i-tý a j-tý mafián znají, 0 pokud se neznají.

Toto řešení se dá vylepšit. Když si totiž uvědomíme, že ověřujeme-li pevnost vztahů pro některého mafiána, víme, že všichni předchozí, tudíž i všichni mafiáni s nimiž navazuje vztahy, jsou pevnými články. Označme zkoumaného mafiána M_x a jeho známé M₁ až M_k v pořadí, v jakém se přidali k mafii. Mafián M_k je tedy "služebně nejmladší" ze známých M_x a víme o něm, že je pevným článkem, tedy zná-li se mafián M_k se všemi mafiány M₁,… ,M_k-1, určitě se znají libovolní dva z nich (jinak by M_k nebyl pevným článkem). V takovém případě se vzájemně znají všichni M₁,… ,M_k, a M_x je tedy podle naší definice pevným článkem. Naopak, pokud M_k nezná některého z M₁,… ,M_k-1, existují dva známí M_x, kteří se neznají, a on je tudíž slabým článkem.

Abychom zjistili, zda je M_x pevným článkem, stačí ověřit, jestli M_k zná všechny M₁,… ,M_k-1, stejným způsobem, jako v minulém řešení. Jelikož nám tentokrát stačí zkontrolovat pouze k vztahů, přijmout jednoho mafiána dokážeme v lineárním čase. Paměti budeme opět potřebovat kvadraticky, jelikož si opět pamatujeme matici známostí. To bychom mohli vylepšit tak, že nahradíme tabulku polem spojových seznamů kde bude pro každého mafiána uložen seznam jeho známých. Tím bychom docílili lineární paměťové složitosti v závislosti na počtu vztahů.

Tolik moje řešení. A teď ta vaše … většinou jste přišli na tu jednodušší variantu, ačkoli jste se dost rozcházeli v názorech na její časovou složitost - jedni psali O(N³), druzí O(N²), což je obojí správně, ale mnozí nenapsali co za tu dobu udělají - jestli prověří jednoho mafiána, nebo všechny. Pokud taková řešení neměla nějaké evidentní nedostatky (například absolutní nedostatek zdrojového kódu), byla oceněna pěti body. Za nedostatečné zdůvodnění správnosti jsem strhla body pouze u rychlejší varianty řešení.

Program

Tereza Klimošová

19-3-6 Prolog (Zadání)

1. Kozel zahradníkem

Pojďme se podívat, jakým způsobem můžeme osázet našich N záhonků. Označme si počet možností osázení N záhonků jako p_N. Stojíme tedy na zahrádce a přemýšlíme, co vysadíme na první záhonek. Když vysadíme na první záhonek mrkev, můžeme si na zbylý druhý, třetí a všechny zbylé vysadit libovolné plodiny. Vysazením mrkve ztratíme jeden záhonek a na zbylém se problém s počtem kombinací opakuje, můžeme si tedy poznačit, že vysazením mrkve způsobíme, že budeme mít p_N-1 kombinací výsadby. A co když vysadíme na první záhonek petržel? Potom na druhý záhonek musíme zákonitě vysadit mrkev, takže přijdeme o 2 záhonky a na zbylých N-2 záhoncích se problém opakuje. Pro N záhonků tedy dostáváme vzoreček p_N = p_N-1 + p_N-2. Startovní podmínky si spočítáme ručně a máme krásnou rovnici přímo si říkající o rekurzivní řešení.

Mimochodem, tato posloupnost je ve skutečnosti veleznámá Fibonacciho posloupnost. Tato posloupnost je v matematice jedna z nejzajímavějších a existuje spousta jevů, které se takto chovají. Tak například si představte, že stoupáte na schodišti, které má N schodů a smíte udělat buď krok na následující schod, nebo krok ob dva schody. Počet možných výstupů na schodiště je (překvapivě) N-té Fibonacciho číslo. Úplně původní je úloha Fibonacciho králíci: Máte dva nově narozené králíky, samečka a samičku. Králičí samička má od věku 1 měsíce jeden pár malých králíčat (samečka a samičku) každý měsíc a nikdy neumírá. Mezitím samozřejmě dorůstají další páry a od věku jednoho měsíce mají další pár králíků, a tak dál. Kolik králičích párů budete mít za rok? Pokud vás zajímají další úlohy na Fibonacciho čísla, nebo jak třeba Fibonacciho čísla souvisí s tzv. zlatým řezem, podívejte se na stránky https://r-knott.surrey.ac.uk/Fibonacci/fib.html a http://en.wikipedia.org/wiki/Fibonacci_number.

Ale vraťme se zpět k výpočtu N-tého Fibonacciho čísla. Jako první nápad jsme měli počítat je přímo podle definice, tedy

fib(N,F) :- N1 is N-1, fib(N1,F1), 
            N2 is N-2, fib(N2,F2), 
            F is F1 + F2.

To je samozřejmě strašlivě pomalé, protože počítáme stále dokola čísla, která už jsme dávno spočítali.

Budeme si tedy čísla budovat odspodu. Začneme se startovními hodnotami 0 a 1 a budeme vždy postupně sčítat poslední dvě čísla, přesně tak, jako bychom vytvářeli řadu na papíře, kdybychom si ji sami počítali. Důležité je pozorování, že v každém okamžiku si stačí pamatovat poslední dvě čísla F1, F2, ta sečíst F3 is F1 + F2 a do dalšího kroku si zapamatovat F2 a F3. Kroky opakujeme, dokud nenasčítáme N-té číslo. Vidíme, že tento postup je lineární vzhledem k N.

Spočítat N-té Fibonacciho číslo jde i v logaritmickém čase pomocí násobení matic. Programovat tento výpočet v Prologu je odvážný počin, který jsme ohodnotili bonusovými body.

2. Stromeček

Mírně přeformulujeme zadání úlohy: V zadaném setříděném vstupním seznamu máme najít prostřední prvek, ten dát do kořene vytvářeného binárního vyváženého stromu, do levého podstromu dát prvky, které byly vlevo od prostředního prvku (tedy první polovinu seznamu) a do pravého podstromu dát prvky, které byly vpravo od prostředního prvku (tedy pravou polovinu seznamu). No a protože levý a pravý podstrom jsou také binární vyvážené stromy, můžeme se na levou a pravou půlku pustit rekurzivně. Rekurze nám vrátí vyrobený správný levý a pravý podstrom, které připojíme pod kořen. Protože seznam byl už na začátku setříděný, zachováme i vlastnost binárního vyhledávacího stromu, tedy prvky vlevo od kořene budou menší a prvky vpravo od kořene budou větší. Podle tohoto návodu je snadné napsat jednoduchý program v Prologu. Měli bychom si ale uvědomit, jak dlouho tento postup bude trvat.

Na každé úrovni musíme vždy hledat prostřední prvek seznamu a seznam dělit na levou a pravou část - to trvá lineárně vzhledem k délce seznamu. A kolik těch úrovní je? Tolik, kolikrát můžu vydělit délku seznamu číslem 2, což je matematicky vyjádřeno číslo log₂N. Tedy dohromady je časová složitost takového postupu O(N log N).

Jistě už tušíte, že míříme k rychlejšímu, lineárnímu řešení. Ve skutečnosti je překvapivě jednoduché.

Základem řešení bude rekurzivní procedura, která dostane seznam a k němu zadaný počet prvků K. Tato procedura bude mít za úkol ukousnout ze začátku seznamu K prvků a z nich vyrobit binární vyvážený strom, který vrátí zpátky jako výsledek. Zároveň procedura vrátí zbytek seznamu, který pro výrobu stromu nepoužila, tedy prvky za K-tým prvkem.

Seznam tedy nebudeme v průběhu výpočtu vůbec dělit na levou a pravou část. Na začátku výpočtu si spočítáme, jak dlouhý je seznam a vypočítanou délku seznamu N vydělíme dvěma K1 is N // 2. Pak se rekurzivně pustíme „sami na sebe“, předáme si celý seznam (žádné dělení na levou a pravou část) a předáme si číslo K1. Jinými slovy, požádáme rekurzivní proceduru, aby si ze vstupního seznamu ukousla potřebných K1 prvků, z nich vyrobila vyvážený binární podstrom, ten nám vrátila a ještě nám vrátila nepoužitý zbytek seznamu. Vrácený vyrobený podstrom použijeme samozřejmě jako levý podstrom vytvářeného binárního stromu. Ze zbylého seznamu, který se nám vrátil z rekurze, utrhneme hlavu a ta bude kořenem vytvářeného binárního stromu (protože K1 jsme zvolili jako polovinu z délky původního vstupního seznamu). Po utrhnutí hlavy nám, jak už jistě vidíte, zůstane právě pravá půlka seznamu, kterou opět rekurzivně zpracujeme s číslem K2 is N - K1 - 1.

Program

Jana Kravalová