Třetí série devatenáctého ročníku KSP
Celý leták v PDF.
- Termín série: 29. leden 2007
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 19-3-1: Jezírka
- 19-3-2: Inventura ve spíži
- 19-3-3: Nevěrné ženy
- 19-3-4: Nejbližší rostoucí posloupnost
- 19-3-5: Pevné vztahy
- 19-3-6: Prolog
Zadání třetí série devatenáctého ročníku KSP
Probudil jsem se a zamžoural do denního světla. Zlověstné ticho rušil jen můj
dech a vzdálené šumění stromů. Rozhlédl jsem se kolem sebe. Postel vedle mě byla
prázdná, ale vyležený důlek naznačoval, že společný útěk s mojí novou známou
nebyl jen sen. Ale kam se poděla? Rychle jsem se oblékl a vyběhl z chaty ven.
Stála na verandě s hrnkem ranní kávy a zírala do mlhy, která obklopovala chatu
jako rozlité mléko.
„Ehm, brý ráno,“ vymáčkl jsem ze sebe a podrbal se v týlu.
„Dobré ráno,“ odvětila a stále hleděla do mlhy. „Máme tu malý problém…“
Upřel jsem pohled přibližně stejným směrem, kterým se dívala ona, a opravdu.
„To jsou ty tvoje křišťálové studánky,“ ušklíbla se jízlivě.
Všude, kam až mé oko v té mlze dohlédlo, se rozprostírala jezírka. A aby toho
nebylo málo, stavěli mezi nimi bobři své vodní cesty.
19-3-1 Jezírka (10 bodů)
Bobři ve svém teritoriu udržují N jezírek. Mezi jezírky mohou vést obousměrné vodní cesty, které umožňují bobrům rychlé přesouvání z jezírka do jezírka. Každá taková cesta má nějakou kladnou délku (což je přirozené číslo, protože bobři s reálnými čísly pracovat neumějí).
Na počátku žádné cesty nevedou. Každou noc vyrobí kanci, jejichž zemních prací bobři hojně využívají, novou vodní cestu mezi dvěma jezírky. Každé ráno se sejde Bobří rada a ta se rozhodne, zda nově vytvořenou cestu přijmou bobři k udržování, či nikoliv. Aby se mohli bobři rozhodnout, potřebují vědět, zda po přijmutí této cesty budou propojena všechna jezírka, a jaký je součet délek udržovaných cest. Nezapomeňte, že udržování cesty něco stojí a bobři chtějí udržovat co nejméně cest (resp. co nejkratší součet délek těchto cest).
Máte tedy dán počet jezírek N, přičemž jezírka jsou číslována od 1 do N. Každé ráno za vámi bobři přijdou a řeknou vám, jaká cesta byla vytvořena (tzn. čísla jezírek odkud kam vede a její délku). Vy aktualizujete vaše data a ihned (tj. před načtením dalšího vstupu, tj. před načtením cesty vytvořené další den) jim oznámíte, zda už jsou všechna jezírka propojena a vypíšete minimální délku udržovaných cest. Cílem je, aby všechna jezírka byla propojena co nejdříve, a v každém kroku byl součet délek udržovaných cest co nejmenší.
Příklad: Buď N=4 a na vstupu cesty z tabulky:
| Denní cesty | Okamžitý výstup |
| 1↔2 délky 5 | Jezírka nespojena, délka udrž. cest 5 |
| 2↔3 délky 6 | Jezírka nespojena, délka udrž. cest 11 |
| 1↔3 délky 4 | Jezírka nespojena, délka udrž. cest 9 |
| 2↔3 délky 8 | Jezírka nespojena, délka udrž. cest 9 |
| 2↔4 délky 3 | Jezírka spojena, délka udrž. cest 12 |
| 1↔4 délky 1 | Jezírka spojena, délka udrž. cest 8 |
„Měli bychom se vydat co nejdříve na cestu,“ pronesla má společnice, když
dopila svou kávu. „Podívej, támhle hloubí další cestu a támhle ještě dvě!“
„To ano, ale nejdřív bych rád něco snědl. Není tu něco … jedlého?“
Přikývla. „Vzadu jsou celkem slušné zásoby konzerv, sucharů a jiných věcí, které
vypadají jedle.“
Sebral jsem odvahu a vydal se proslídit spíž. Ať ta chata patřila
komukoli, musel to být podivín. Od každé potraviny měl přesně sedm kousků.
Sedm konzerv lančmítu, sedm konzerv párků, sedm balíků sucharů …Zajímalo by mě, jestli až se sem dotyčný vrátí, pozná, že mu něco schází.
19-3-2 Inventura ve spíži (6 bodů)
Je dáno pole Spíž velikosti N, ve kterém jsou uloženy potraviny ve spíži. Na každé pozici i se nachází nějaká potravina Spíž[i]. Potraviny jsou označeny čísly, avšak nemusejí být číslovány souvisle a max(Spíž[i]) může být klidně mnohem větší než N.
Dále dostanete číslo k a máte vypsat, které potraviny se v poli Spíž vyskytují právě k-krát.
Příklad: Pro k=2 a potraviny 1234, 654321, 1234, 5 máte vypsat, že dvakrát se vyskytuje jenom potravina s číslem 1234.
Po krátké ale výživné snídani jsme se vydali na cestu. Po slalomu mezi jezírky
se před námi objevila lesní pěšina.
„Bezva. Tahle pěšina vede přímo k hlavní silnici, tam nám stačí zastavit
nějaké auto a máme vyhráno,“ prohlásila sebejistě a vydala se napřed.
„Jak to můžeš vědět?“
„Znám to tu. Tahle chata totiž patří Angelu Criminallisovi. To je jeden
z Carlových právníků.“
Chvíli jsme pokračovali mlčky a můj mozek pracoval na plné obrátky. Jak je to
možné? Že by se tak dobře znala s nějakým poskokem samotného Carla Assassina?
Jedině že by …
„Předpokládám, že tvůj manžel o téhle chatě neví,“ pronesl jsem jen tak
polohlasem.
„Ne, neví,“ odpověděla stroze. Otočila se na mě a pozvedla obočí.
„Ale, potom … jak to!? Vždyť by tě zabil!“
Vzpomněl jsem si na jeden případ, který se stal asi před rokem. Bylo to ve všech
novinách. Několik mafiánů zavraždilo svoje manželky v jeden den. A pochopitelně
jim to prošlo. Tehdy se říkalo, že je zabili, protože jim byly ženy nevěrné, ale
copak může něco takového ospravedlnit vraždu?
19-3-3 Nevěrné ženy (7 bodů)
Mafiáni jsou mocní lidé. Každý mafián ví o všech ostatních mafiánech téměř všechno. Také ví, kterého mafiána podvádí žena a kterého ne. Bohužel to ale žádný mafián neví o své ženě, a tak ji zkrátka věří. V okamžiku, kdy mafián zjistí že ho žena podvádí, tak ji přesně v poledne následujícího dne veřejně zabije (tzn. dozví se to všichni ostatní mafiáni).
Všichni spokojeně žili až do chvíle, kdy se na jednom večírku jeden mafián strašně opil a nechtěně před všemi přítomnými prohlásil: „Alespoň jedna žena tady podvádí svého muže.“ Devatenáct dní nato byly všechny nevěrné ženy nalezeny krátce po poledni mrtvé. Kolik těchto žen bylo a jak na to podvedení mafiáni přišli?
Abychom předešli častým dotazům, shrneme zde zadání a upřesníme některá fakta:
- každý mafián ví o všech ostatních mafiánech zda je podvádí ženy,
- žádný mafián neví o své ženě, zda ho podvádí a nemůže se to nijak přímo dozvědět (nikdo mu to neprozradí – ani nedobrovolně, nikde to nevyčte atp.),
- podvádění je binární – každá žena buď podvádí, nebo ne (jiné stavy nejsou),
- pokud mafián přijde (logickou úvahou) na to, že ho žena podvádí, zabije ji následující den přesně v poledne (tzn. čas je diskrétní, kvantovaný na dny),
- mafiánů je mnoho (pro vaše úvahy můžete předpokládat, že je jich více, než libovolná konečná konstanta),
- všechny vraždy se odehrály najednou v poledne 19. dne (večírek se konal 0. dne) a předtím ani potom se žádné jiné vraždy neudály.
Chceme po vás, abyste zjistili, kolik žen bylo zavražděno. Zároveň popište deduktivní postup mafiánů, jak přišli na to, že jsou jim ženy nevěrné.
„Ale ne,“ usmála se. „S Angelem jsem se seznámila až po tomhle incidentu.“
Mlčky jsme pokračovali dál. Po pár hodinách nám zvuk projíždějících aut a
řídnoucí les napověděl, že se blížíme k silnici. Mávnutí rukou a její
okouzlující úsměv zastavil první kolemjedoucí auto. Řidič byl lehce nevrlý, když
zjistil, že stopujeme dva, ale nakonec se nechal přesvědčit, aby nás odvezl
k nejbližšímu motorestu.
Motorest nepatřil zrovna k nejnovějším, nebo snad dokonce nejluxusnějším.
Sebejistým krokem vešla dovnitř a kývnutí číšníka na pozdrav dávalo tušit, že ji
tu nevidí poprvé. Prošla celým lokálem a sebejistě vkročila do kuchyně.
V tichosti jsem ji následoval a čekal, co se bude dít.
„Jak jdou kšefty, Marconi?“ usmála se na kuchaře a zřejmě i majitele v jedné
osobě. Kuchař jí úsměv oplatil: „Znáš to, bývalo líp.“
„Mohl bych si zavolat?“ vnořil jsem se do jejich uvítacího rozhovoru.
„A koho chceš prosím tě volat?“ podívala se na mě skoro pobaveně.
„No přece policii.“
Kuchařů úsměv zamrzl a v jeho ruce se s neuvěřitelnou rychlostí objevil velký
kuchyňský nůž. Snad by ho i použil, ale ona ho zadržela.
„Policii? Proboha proč? Poldové jsou buď zkorumpovaní nebo si hledí svých
problémů, aby si to náhodou u někoho nerozlili.“
„Mám tam známého … jmenuje se detektiv Zamříž a několikrát už mi pomohl.
I z horších malérů,“ vypravil jsem ze sebe skoro ublíženě. Na chvíli se
zamyslela.
„Když nad tím tak přemýšlím, stejně nemáme co ztratit.“
Kývla na Marconiho a ten mě nevrle zavedl k telefonu. Vytáhl jsem z kapsy
papírek s telefonním číslem, ale ouha. Papírek byl celý zmačkaný a některé
číslice byly špatně čitelné. Naštěstí jsem si pamatoval, že posloupnost čísel
tvořících telefonní číslo je ostře rostoucí.
19-3-4 Nejbližší rostoucí posloupnost (13 bodů)
Máme posloupnost čísel a1,a2, …, an. Chceme najít takovou ostře rostoucí posloupnost b1,b2, …, bn, aby byla „co nejpodobnější“ posloupnosti a1,…, an. (Slovy ostře rostoucí posloupnost myslíme to, že každý prvek je větší než předchozí.)
| n |
| i=1 |
Příklad: Pro posloupnost 9,4,8,20,14,15,18 je nejlepší například 6,7,8,13,14,15,18. Vzdálenost této posloupnosti od původní je |6-9|+|7-4|+|8-8|+|13-20|+|14-14 |+|15-15 |+|18-18 |=3+3+0+7+0+0+0=13.
Po několika nesprávných pokusech jsem se konečně dovolal. Zamříž si vyslechl můj
problém a slíbil, že se pro nás zajede svým vozem.
Netrvalo dlouho a ocitli jsme se na policejní stanici v Zamřížově kanceláři.
Zamříž se pečlivě probíral papíry ukořistěnými v Assassinově trezoru. Napadlo
mě, že po všem, co jsem s Assassinovou manželkou prožil, neznám ani její křestní
jméno. Není nic jednoduššího, než se zeptat, ale tehdy mě to stálo chvilku
přemáhání.
„Isabela,“ odpověděla a obdařila mě jedním z těch úsměvů, po kterém se
chlapům podlamují kolena. I mně by se podlomila, kdybych neseděl na židli.
„Nerad vám ruším romantickou chvilku,“ přerušil nastalé ticho Zamříž,
„ale tohle nebude tak jednoduché. Mafiánské vztahy jsou příliš komplikované
na to, abychom teď mohli libovolného mafiána zavřít.“ Opřel se v křesle a
zapálil si doutník. „Kdybychom tak našli slabý článek v jeho organizaci…“
19-3-5 Pevné vztahy (10 bodů)
Abychom zjistili, jak pevné vztahy jsou mezi jednotlivými členy mafiánské organizace, musíme sledovat, jak tyto vztahy vznikly. Když přijde nový mafián X do organizace, naváže vztahy s několika dalšími mafiány M1,…, Mk. Aby vztahy byly pevné, musí v tu chvíli být mezi každými dvěma mafiány Mi, Mj už nějaký vztah.
Na počátku je mafián pouze jeden a ten si začíná budovat organizaci. V každém kroku dostane váš algoritmus nového mafiána a neprázdný seznam již existujících mafiánů, se kterými navazuje vztahy při přijetí do organizace. Algoritmus prověří, zda jsou všichni stávající mafiáni, ke kterým se chce nováček připojit, vzájemně propojeni (mezi každými dvěma jsou nějaké vztahy). Pokud je vše v pořádku, algoritmus začlení nového mafiána do organizace a pokračuje příjímáním dalšího mafiána. V opačném případě ohlásí, že tento nový mafián by byl slabým článkem, a skončí. Algoritmus buď nalezne první slabý článek v mafiánské organizaci a hned skončí, nebo oznámí, že organizace má pevné vztahy.
Příklad: Na začátku je jediný mafián. K mafii se připojují následující mafiáni:
| Nový mafián | Navazuje vztahy s mafiány |
| 2 | 1 |
| 3 | 1,2 |
| 4 | 2,3 |
| 5 | 1,2,4 |
| 6 | 4 |
Program by měl vypsat, že mafián 5 byl slabým článkem. (Mafiáni 1 a 4 nemají mezi sebou žádný vztah.)
Seděl jsem v Zamřížově kanceláři, poslouchal jeho výklad o vztazích mafiánů a má nálada rychle klesala. Byla policie opravdu tak zbabělá, nebo měl Zamříž pravdu a svržení jednoho mafiána by vyústilo v obrovské nepokoje a vlnu násilností? Moji mysl zaplavovala beznaděj. Co teď, když nám ani policie nepomůže? Nebo pomůže? Tázavě jsem se zahleděl na mého kamaráda…
To be continued…
19-3-6 Prolog (12 bodů)
Milí pokročilí programátoři v Prologu,
vítáme vás u třetího kurzu programovacího jazyka Prolog. Z mnoha došlých řešení a hojných bodových zisků 1. série je vidět, že jste úvodní díl dobře pochopili. Přesto vám doporučujeme přečíst pozorně povídání k vzorovému řešení 1.série. Pokusili jsem se do něj propašovat několik zajímavých informací, které by se vám při dalším řešení mohly hodit.
Ale teď už se pojďme podívat na další zajímavou pasáž z jazyka Prolog.
Aritmetika
Počítání s čísly je v Prologu, jako všechno ostatní,
trošku… jiné. Prolog samozřejmě umí sčítat, odčítat, porovnávat,
přiřazovat, atd., ale musíme u toho být opatrní. Na začátek jeden
příklad. Chceme sečíst 1 + 2 a přiřadit výsledek do proměnné X
(tedy, chceme výsledek zunifikovat s proměnnou X). Snad každý by
intuitivně napsal něco jako
To ale nefunguje tak, jak bychom chtěli, totiž nedostaneme kýžený
výsledek 3. Jak jsme si říkali v minulém díle, operátor = vyvolává
unifikaci na své argumenty, takže místo sčítání se dočkáme toho, že do
proměnné X se zunifikuje výraz 1+2 tak, jak je. Pokud chceme
opravdu vyvolat aritmetickou operaci, musíme tam, kde bychom
v matematice použili =, použít is.
V tomto případě se skutečně vyhodnotí aritmetický výraz 1 + 2 a do X se zunifikuje číslo 3.
Použití operátoru is má ale svá úskalí. Jak si jistě pamatujete,
jednou zunifikovanou proměnnou už nesmíme znovu unifikovat za něco
jiného. Nová unifikace se provádí jen a pouze, pokud zkoušíme novou
větev rekurzivního výpočtu. To platí i pro operátor is. Pokud
napíšeme
tak pokud X ještě nebyla zunifikovaná, zunifikuje se na 3. Pokud
už ale zunifikovaná byla, například na 4, místo přiřazení se
porovnají hodnoty 3 a 4 a výsledkem bude samozřejmě No. Toto má
pro nás trošku nepříjemné důsledky – pokud potřebujeme do proměnné
uložit novou hodnotu, musíme si vyrobit i novou, dosud volnou
proměnnou a do ní si novou hodnotu uložit. Podívejte na tento
příklad. Budeme počítat délku seznamu:
Délku seznamu počítáme rekurzivně. Nejprve si necháme spočítat délku
zbytku seznamu (Telo) do proměnné Delka2 a poté přičteme jedničku
za to, že jsme seznamu utrhli hlavu. Musíme ale použít dvě proměnné,
Delka a Delka2.
Druhé omezení na predikát is říká, že kdykoliv chceme vyhodnotit
nějaký aritmetický výraz na pravé straně, musí být všechny proměnné
v něm již unifikované. Příkaz
neuspěje, pokud Y není unifikována nějakou konkrétní
hodnotou. Pozor tedy na pořadí predikátů v následujícím příkladu:
S takovým výpočtem samozřejmě pohoříme, výpočet výrazu Delka2 + 1
neuspěje, protože proměnná Delka2 se unifikuje až v dalším
predikátu.
Stejným způsobem jako is se vyhodnocují i další operátory
=.= | aritmetická rovnost |
=\= | aritmetická nerovnost |
< | je menší |
> | je větší |
=< | je menší nebo rovno |
>= | je větší nebo rovno |
a samozřejmě +, -, *, …
Ukážeme si ještě jeden zajímavý příklad, tentokrát máme pole a chceme
na n-tou pozici vložit hodnotu K a vrátit výsledek v proměnné
NSezn.
Postupujeme tak, že si postupně odpočítáváme N. Pokud už je N
rovno 0, jsme na správném místě v seznamu a vložíme prvek K do
hlavy seznamu. Pokud je N ještě příliš velké, odtrhneme seznamu
hlavu, od N odečteme jedničku a pustíme se rekurzivně na zbytek
seznamu. Rekurze nám vrátí zbytek seznamu se správně zařazeným prvkem
K. Před tento zbytek nesmíme zapomenout předřadit hlavu seznamu,
kterou jsme předtím odtrhli.
Stromy
Než začnete číst tuhle kapitolu, doporučujeme přečíst si, co to je binární strom. Pěkný obrázek binárního stromu je na stránce http://cs.wikipedia.org/wiki/Binární_strom. Povídání o binárních vyhledávacích stromech najdete na stránce http://ksp.mff.cuni.cz/tasks/18/cook4.html. Vyzbrojeni znalostmi se teď můžeme pustit do programování stromů v Prologu.
Nejprve potřebujeme vymyslet pěknou strukturu reprezentující jeden uzel stromu. V uzlu obvykle chceme ukládat nějakou hodnotu a potom levý a pravý podstrom. Použijeme tedy následující strukturu:
t(L,H,R) znamená, že L je levý podstrom, H je hodnota uložená v daném stromě a R pravý podstrom.
Ještě potřebujeme atom pro prázdný strom, ať je to tedy nil.
Následující strom
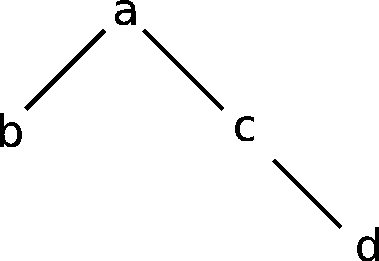
Abychom nemuseli strom v interpreteru neustále zadávat, uložíme si jej takto:
Pak se na něj můžeme odkazovat dotazy
A jak tedy budeme se stromy pracovat? Jednoduše, protože sám Prolog jako rekurzivní jazyk nám nabízí prostředky pro pohodlný průchod stromu:
Tento průchod stromem nám dá na výsledku seznam všech uzlů v daném
stromu. Všimněte si pořadí průchodu stromem – jakmile přijdeme do
nějakého uzlu, nejprve se pustíme do levého podstromu, potom do
pravého podstromu, výsledné seznamy uzlů z levého a pravého podstromu
spojíme predikátem conc do jednoho seznamu, před který přiřadíme
hodnotu z aktuálního vrcholu. Výsledný seznam na našem stromě
muj_strom tedy bude [a,b,c,d].
Poznámka: Predikát conc si coby pokročilí programátoři v Prologu
dokážete jistě napsat sami.
P.P.P Pěkné Programování v Prologu
Aby váš program měl všech „pět P“ a vypadal jako napsaný opravdovým znalcem, přidáváme tentokrát kapitolu o dobrém prologovském stylu:
Poznámky v Prologu vypadají takto:
% Cokoliv za tímto znakem do konce řádky se ignoruje
Před každý nový predikát je třeba napsat, jak se predikát jmenuje, kolik má parametrů, jaké vstupy očekává a co dělá. Dále můžete vsouvat kratičké komentáře k jednotlivým řádkům programu.
Pokud napíšete velmi dlouhé pravidlo, můžete jednotlivé predikáty z těla pravidla odsadit na další řádek a mírně je posunout doprava, aby se program zpřehlednil, asi takto:
Proměnné místo X, Y, pojmenovávejte radši Sez, Posl,
Head a podobně, aby alespoň trošku prozrazovaly, co skrývají.
Vyhněte se zbytečné unifikaci pomocí =. Kde to jde, unifikujte v parametrech predikátů:
Ladění prologovského programu můžete udělat tak, že necháte prologovský interpret sledovat všechna volání zvoleného predikátu, takto:
Od tohoto okamžiku bude Prolog vypisovat, s jakými parametry se volá daný predikát, kdy uspěl a kdy se co zkouší znovu…
Kvíz
♠ Co odpoví Prolog na dotaz:1 + 2 = 2 + 1.
Yes.No.- Nastane běhová chyba.
Odpověď: Operátor = vyvolá unifikaci na termech, které nejsou stejné, proto Prolog odpoví No.
♠ Co odpoví Prolog na dotaz: 2 + 3 =.= 3 + 2.
Yes.No.- Nastane běhová chyba.
Odpověď: Operátor aritmetického porovnání =.= nejprve vyhodnotí oba výrazy na 5, a tedy Prolog odpoví Yes.
♠ Co odpoví Prolog na dotaz: X < 3.
Yes.No.- Nastane běhová chyba.
Odpověď: Výraz vlevo nelze vyčíslit, nastane tedy běhová chyba.
Soutěžní úložky
1. Kozel zahradníkem (5 bodů) Kozel sází mrkev a petržel na své
zahradě. Má k dispozici N záhonků, na jednom záhonu smí být právě
jedna plodina. Sadba ale není tak jednoduchá a některé plodiny
vyžadují zvláštní způsob rozmístění na záhonku. Tak například dvě
petržele nikdy nesmí být zasazeny vedle sebe. Tedy například mmmpm
je správná výsadba, ale mmppm není správná výsadba. Napište
v Prologu program, který pro daný počet záhonů N určí, jaký je počet
všech možných rozesazení mrkve a petržele na záhoncích. Nemusíte
vypisovat, jakým způsobem jsou plodiny vysázeny, stačí jen počet
možností. Snažte se program urychlit na lineární časovou složitost
(vzhledem k počtu záhonů).

Příklad: Pro N = 2 je počet všech správných vysázení roven 3. Konkrétně je to mm, mp, pm.
2. Vánoční stromeček (7 bodů) Vánoční nadešel čas… a vy jste se rozhodli nazdobit vánoční stromeček. Máte sadu vánočních ozdob očíslovaných přirozenými čísly ve vzestupném pořadí. Váš vánoční stromeček, protože jste informatici, nevypadá nijak jinak nežli jako binární vyhledávací strom, který má v každém uzlu jednu vánoční ozdobu. A jelikož jste dobří informatici, chcete z ozdob postavit perfektně vyvážený binární vyhledávací strom, tedy takový strom, kde pro každý uzel platí, že počty uzlů v jeho levém a pravém podstromě se liší maximálně o jedna. Prostě a jednoduše nechcete, aby se váš vánoční stromeček nakláněl a nedejbože se třeba ještě někam zřítil.
Vaším úkolem je napsat v Prologu program, který ze vstupního seznamu
vyrobí perfektně vyvážený binární strom. Vstupní seznam je seznam
vzestupně setříděných přirozených čísel, tedy například
[3, 6, 8, 9, 10]. Možné řešení úlohy na vstupním seznamu [3, 6, 8, 9, 10]
je třeba
Špatné řešení by bylo
Pozor, vaším úkolem je napsat celý program. Kdykoli použijete
jakýkoli predikát, musíte k němu připsat kód, v žádném případě nestačí
napsat „použijeme predikát predek z učebního textu“ nebo něco
podobného.