Třetí série dvacátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

Teoretická úloha27-3-1 Plocha k přistání (Zadání)

Většina z vás asi ví, jak se největší bílá oblast hledá, pokud jde o obyčejný bitmapový obrázek. Na obrázek se lze dívat jako na graf, kde pixely představují vrcholy a každá dvojice sousedních bodů je spojena hranou (tedy graf má tvar mřížky). V takovémto grafu bychom chtěli najít „komponenty bílé souvislosti“ – tedy maximální souvislé části grafu, které jsou celé bílé. K tomu můžeme použít klasický algoritmus na hledání komponent souvislosti prohledáváním do šířky či hloubky (pokud jej neznáte, nahlédněte do naší grafové kuchařky), jen s tím rozdílem, že při prohledávání zcela ignorujeme černé vrcholy – vůbec je nenavštěvujeme. Snadno si rozmyslíte, že takto získáme očekávaný výsledek. Průběžně počítáme velikost nalezených komponent a nakonec jen vybereme maximum. Na tento postup jde pohlížet také jako na opakované použití klasického algoritmu flood fill.

Zkusme se tím inspirovat. I kvadrantový obrázek má něco jako „pixely“, tedy elementární jednobarevné plochy – jsou to všechny nepodrozdělené čtverce. Jen je každý jinak velký a může mít víc než čtyři sousedy. Navíc není vůbec jasné, jak tyto sousedy najít. Ale pokud by nám někdo dal graf, jehož vrcholy jsou elementární čtverce ohodnocené svou plochou a hrany představují jejich sousednosti, dokázali bychom už jednoduše úlohu vyřešit.

Graf sousednosti může vypadat například takto (tučně jsou vyznačeny bílé komponenty):

Kvadrantový obrázek a jeho graf sousednosti

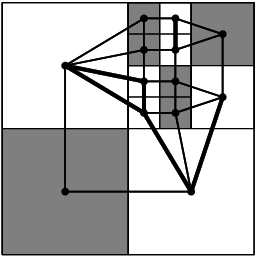
Zbytek řešení bude pojednávat o tom, jak si takový graf pořídit, a to hned dvěma různými způsoby. Na úvod ovšem povězme pár věcí oběma řešením společných. Řešení víceméně každé úlohy nad kvadrantovým kódem začíná tím, že z kódu vytvoříme takzvaný kvadrantový strom. Kořen tohoto stromu reprezentuje celý obrázek. Pokud je jednobarevný, pamatuje si svou barvu a nemá žádné potomky; v opačném případě má právě čtyři syny představující kvadrantové stromy pro jednotlivé čtvrtiny.

Strom pro kvadrantový kód (0((1010)1(0101)0)10) (odpovídá obrázku výše) vypadá takto:

Kvadrantový strom

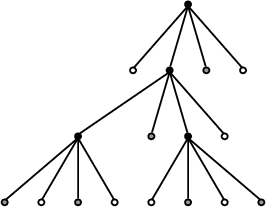
Každý vrchol kvadrantového stromu představuje čtverec 2r×2r, kde r je takzvaný řád vrcholu (čtverce). Kořen má řád h (výška stromu), jeho synové h-1, atd.

Strom vytvoříme přímočarou rekurzivní funkcí. Pokud se vyhneme zbytečnému kopírování řetězců (například si kód uložíme v globální proměnné a rekurzivním voláním budeme předávat jen index znaku, od kterého začít), zvládneme to v lineárním čase. Podrobněji ve zdrojáku.

Řešení průchodem do šířky

Graf sousednosti vytvoříme tak, že pro každý jednobarevný čtverec (tomu odpovídá list kvadrantového stromu) najdeme seznam jednobarevných čtverců s ním v obrázku sousedících. To je ale těžké, neb jeden čtverec může mít sousedů hodně, a to i v docela vzdálených částech stromu. Nám ovšem stačí, když každou sousednost „objeví“ jen jeden ze zúčastněných čtverců, např. ten menší. Pak nám stačí pro každý čtverec hledat jen sousedy stejného nebo vyššího řádu (příslušné listy jsou ve stromu stejně vysoko nebo výš). A takový je v každém směru nejvýše jeden. Tím získáme všechny hrany grafu sousednosti orientované směrem od menšího čtverce k většímu, opačný směr doplníme jejich otočením, což můžeme dělat i průběžně. Z toho je také hned vidět, že hran je lineárně mnoho.

Samotné hledání sousedů provedeme průchodem stromu po patrech (neboli do šířky od kořene). Když navštívíme nějaký vrchol v, určíme jeho nejhlubšího (obrázkového) souseda na každé straně, který ale není hlouběji než on sám. Toho si označíme Ss(v) (kde s ∈ {L, P, H, D} je příslušná strana). Všimněme si, že pokud je v tím hlubším z nějaké dvojice sousedních listů, je Ss(v) právě druhým vrcholem této dvojice, a tedy jsme objevili jednu hranu grafu sousednosti (a po průchodu všech vrcholů objevíme všechny). V opačném případě je Ss(v) nějaký vnitřní vrchol stromu, který se ale bude dále při hledání hodit.

To by si určitě zasloužilo obrázek. Abyste se neztratili v obrovském množství čar, ukážeme si to na příkladu jednorozměrného „kvadrantového“ obrázku. To je dlouhá „nudle“ rozměrů 2k×1, která je buď celá bílá, celá černá, nebo rozdělená na dvě poloviny, rekurzivně splňující stejnou definici. Kvadrantový strom takovéhoto obrázku je binární a má tu výhodu, že směr vlevo a vpravo ve stromu odpovídá stejnému směru v obrázku.

Jednorozměrný kvadrantový obrázek
Pomocné odkazy na sousedy v jednorozměrném kvadrantovém stromu

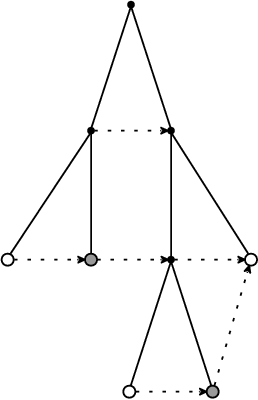
Tečkované šipky značí ukazatele SP (vedou od v k SP(v)).

Zbývá si rozmyslet, jak Ss(v) určit. Pro jednoduchost uvažujme s=P, ostatní směry vyřešíme obdobně. Označme si p rodiče vrcholu v. Pokud čtverec odpovídající v leží v levé polovině čtverce p, stačí vzít správného sourozence v. Např. je-li v levým dolním synem p, SP(v) je pravý dolní syn p. V opačném případě se podíváme na vrchol u := SP(p) (p je ve vyšším patře, tedy jeho S už máme spočítané). Pokud u je list, pak SP(v) = u. Pokud není list, víme, že leží na stejné úrovni jako p (kdyby ležel výš, nebyl by nejhlubším sousedem p, neb některý z jeho synů by také sousedil s p a byl hlouběji). V takovém případě SP(v) musí být jeden ze synů u, ten, který správně přiléhá k v. Například je-li v pravým horním synem p, pak SP(v) je levý horní syn u. Zvlášť musíme ošetřit případ, kdy v je v daném směru na kraji obrázku.

Určení SP(v) nás stojí konstantní čas, tedy celý průchod stromu zvládneme v lineárním čase a v jeho průběhu sestrojíme graf sousednosti jednobarevných čtverců. A už víme, že sestrojení kvadrantového stromu, rozklad grafu sousednosti na komponenty a výběr největší zvládneme rovněž v lineárním čase. Tedy i celý algoritmus si vystačí s O(n) času i paměti, kde n je délka vstupního kódu.

Program (Python)

Řešení průchodem do hloubky

Předchozí řešení vytvářelo sousednosti po hladinách shora dolů. Ukážeme jiný způsob, který postupuje naopak zdola nahoru a dosahuje stejné časové složitosti.

Strom budeme procházet do hloubky a průběžně budovat graf sousednosti. Přesněji řečeno, kdykoliv se při procházení stromu budeme vracet z nějakého čtverce, budou už zaznamenány všechny sousednosti mezi jeho potomky. Sousednosti vedoucí přes hranici aktuálního čtverce doplníme později.

Proto se nám bude hodit předávat do vyšších pater stromu informace o tom, jaké černé a bílé podčtverce leží na hranici aktuálního čtverce. To uložíme do čtyř seznamů. Levý seznam bude popisovat podčtverce přiléhající k levé hraně aktuálního čtverce, uspořádané shora dolů. Z každého podčtverce nás zajímá jen to, jak se dotýká hranice, což je nějaký interval y-ových souřadnic. Za každý interval přidáme do seznamu dvojici (v,r), kde v je příslušný vrchol grafu sousednosti a r řád podčtverce. Podobně vytvoříme pravý seznam (též uspořádaný shora dolů), horní a dolní (oba zleva doprava).

Čtyři hranice jednoho čtverce

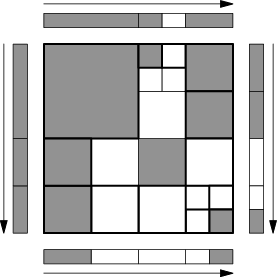
Vracíme-li se z jednobarevného čtverce (listu stromu), nemusíme vytvářet žádné sousednosti. Všechny čtyři seznamy budou obsahovat odkazy na tento čtverec.

Zajímavější věci se dějí, pokud se vracíme z vícebarevného čtverce (vnitřního vrcholu stromu). Nechť Q1 až Q4 jsou kvadranty aktuálního čtverce. Z rekurze už známe sousednosti uvnitř kvadrantů a také podčtverce na hranicích kvadrantů. Nyní potřebujeme rozpoznat sousednosti vedoucí přes hranice kvadrantů a sestrojit hranici celého čtverce.

Jak k sobě patří kvadranty

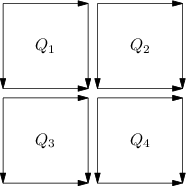
Nejprve vyřešíme hranici: levý seznam celého čtverce získáme spojením levého seznamu kvadrantu Q1 s levým seznamem kvadrantu Q3. Podobně získáme ostatní seznamy slepením seznamů z vnějších hranic kvadrantů.

Nyní sousednosti: uvažujme čtverce sousedící přes společnou hranici kvadrantů Q1 a Q2 (ostatní hranice zpracujeme obdobně), tedy intervaly z pravého seznamu Q1 a levého seznamu Q2. Kdykoliv se interval z Q1 překrývá s intervalem z Q2, chceme propojit hranou příslušné vrcholy v grafu sousednosti.

Propojování probíhá takto: podíváme se na počáteční interval každého seznamu – těmto intervalům říkejme třeba x a y. Pokud jsou stejného řádu, vytvoříme hranu. Pokud se řády liší (bez újmy na obecnosti x má vyšší řád), vezmeme x a z protilehlého seznamu budeme odebírat intervaly, dokud se jejich délky nenasčítají na délku x. (Všimněte si, že k tomu musí dojít přesně na hranici intervalu, neboť všechny intervaly vznikly postupným půlením délky hrany celého obrázku.) Kdykoliv odebíráme nějaký interval, vytvoříme hranu. Poté pokračujeme zbytkem obou seznamů, než se oba vyprázdní. Dopadne to například takto:

Propojování intervalů

(Pokud vám na obrázku chybí hrana např. mezi třetím a čtvrtým intervalem v prvním řádku, uvědomte si, že odpovídá sousednosti v kolmém směru, takže vznikne při propojování jiných seznamů než těchto dvou.)

Umíme tedy zpracovat jak listy stromu, tak jejich vnitřní vrcholy. Nakonec se prohledávání vrátí z kořene stromu a graf sousednosti je hotov.

Zbývá určit časovou složitost. V každém vrcholu stromu strávíme konstantní čas spojováním seznamů – to je celkem O(n) za celý strom – a nějaký další čas zpracováním vnitřních hranic. Vnitřní hranice přitom může být poměrně komplikovaná, ale stačí si uvědomit, že kdykoliv sáhneme na nějaký interval, vypadne tento interval ze svého seznamu a už se nikdy do žádného seznamu nevrátí.

Čas strávený zpracováním všech hranic dohromady je tedy shora omezen počtem všech intervalů, které vložíme do seznamů. Vkládáme ale pouze v listech stromu: 4 intervaly za každý list. Tak vznikne celkem O(n) intervalů, takže jejich odebíráním strávíme čas O(n).

Program (C)

Trampoty s velkými čísly

Danger!Naše algoritmy počítají s délkami intervalů a plochami čtverců jako s normálními čísly. Tato čísla ale rostou exponenciálně s hloubkou stromu, takže by se mohlo stát, že se nevejdou do běžné celočíselné proměnné. Zadání o této možnosti nevinně mlčelo, ale zkusme ji aspoň na chvilku připustit. Držte si klobouky…

První z algoritmů na konstrukci grafu s délkami ani plochami nepočítá, takže ho měnit nemusíme.

Druhý algoritmus používá délky při propojování seznamů intervalů. Můžeme si pomoci takto: podíváme se na intervaly x a y na začátku seznamů. Pokud jsou stejného řádu, nic se nemění. Pokud je (BÚNO) x vyššího řádu, rozdělíme ho na dva intervaly o 1 nižšího řádu a postup opakujeme. Části vzniklé rozdělením zdědí informace o vrcholu grafu a o barvě z původního intervalu. Jako cvičení ponecháváme dokázat, že vytvoříme nejvýše lineárně mnoho nových intervalů (nápověda: představte si strom popisující postupné dělení intervalů).

Hledání komponent souvislosti zůstane beze změny, ale pak potřebujeme spočítat plochy komponent. Nejprve každému čtverci přiřadíme číslo komponenty. Poté projdeme celý strom po hladinách shora dolů, a kdykoli narazíme na jednobarevný čtverec, přidáme ho k příslušné komponentě. Pro každou komponentu tudíž vznikne seznam jejích čtverců uspořádaný sestupně podle řádu.

Nyní v tomto pořadí budeme sčítat plochy čtverců. To jsou potenciálně obrovská čísla. Budeme je zapisovat ve dvojkové soustavě a do paměti ukládat jako seznam pozic jedniček ve dvojkovém zápisu, uložený od nejvyššího bitu k nejnižšímu. Každý další čtverec přitom přispěje plochou, která je menší nebo rovna zatím nasčítané ploše. Můžeme tedy připsat jedničkový bit na konec čísla, jen se nám mohlo stát, že už tam jeden bit tohoto řádu mohl být, takže dojde k přenosu. Vyřizováním všech přenosů ovšem strávíme lineární čas, protože s každým přenosem klesne celkový počet jedničkových bitů o 1. (To je podobná úvaha jako onehdy s intervaly.)

Plochy máme spočítány, zbývá z nich najít maximum. Kdykoliv při tom porovnáváme dvě čísla, procházíme je od nejvyššího řádu a jakmile se přestanou shodovat, porovnávání ukončíme. Čas strávený porovnáváním přitom účtujeme jedničkám v menším z obou čísel, které se už žádného dalšího porovnávání nezúčastní. Takto celkem naúčtujeme každé jedničce čas O(1) a všech jedniček za celou dobu běhu algoritmu vznikne O(n).

I s obrovskými čísly jsme tedy dokázali udržet lineární složitost algoritmu. Kouzlo se podařilo ;-)

Martin „Medvěd“ Mareš & Filip Štědronský

Teoretická úloha27-3-2 Návrhy pro komisi (Zadání)

V úloze se pracuje s řetězci, zkušený řešitel si tedy přečte zadání, zamyslí se a řekne si „Ha, trie!“. To je speciální strom, ve kterém se hranám přiřazují písmenka a cesta od kořene nějak odpovídá vstupním řetězcům; více o ní píšeme v kuchařce o hledání v textu.

Jenže jak přesně trii na naši úlohu použít? Můžeme jednoduše počítat, kolik členů komise schvaluje určité slovo – stačí si do vrcholů přidat počítadlo. Když se pak vydáme od kořene dolů a budeme tyto členy postupně sčítat, zajímá nás, jestli v daném vrcholu součet dosáhne alespoň hodnoty K. Pokud ano, jakýkoliv návrh začínající slovem odpovídajícím aktuálnímu vrcholu bude schválen.

Kolik takových návrhů existuje? Když aktuální hloubku označíme jako d, dá se jejich počet vyčíslit jako 26D-d. Za každý ze znaků, který chybí do přijatelné délky návrhu D, totiž smíme zvolit libovolný znak anglické abecedy.

Také z uzlu, v kterém se nasbíralo alespoň K hlasů, nechceme postupovat níž – všechna možná pokračování budou začínat schvalovaným řetězcem, takže jsme je už zahrnuli. Při dosažení hodnoty K se tedy zastavíme, resp. vrátíme o úroveň výš a necháme procházení postupovat dál.

To zní dobře. Ale bude to opravdu fungovat? Co kdyby nějaký člen schvaloval jak slovo „psa“, tak slovo „psal“? Ouha! To bychom ho započítali vícekrát, což nechceme – a zadání nám rozhodně neslibuje, že taková situace nenastane.

Připomeňme si naznačenou myšlenku: pokud člen (či komise) schvaluje nějaké slovo, schválí i jakékoliv další, které tímto slovem začíná. Kdybychom tedy věděli, že člen už schvaluje nějaký prefix aktuálního slova, můžeme právě zpracovávané slovo s klidem zahodit.

Tady se nabízejí dva přístupy. Můžeme slova každého člena lexikograficky seřadit a přidávat je do trie už seřazená. Jen si musíme rozmyslet, jak v trii komise poznat, zda jsme do aktuálního vrcholu už přičetli hlas právě zpracovávaného člena.

Alternativu, se kterou pracuje i vzorový program, představuje vybudování druhé trie, tentokrát specifické pro člena. Do ní jednoduše naházíme všechna jeho oblíbená slova (značíme si ve vrcholech, jestli tam končí slovo). Následně ji projdeme a vždy, když narazíme na konec slova, odpovídající slovo přidáme do trie pro komisi a hned se vrátíme.

Po zpracování slov všech členů trii projdeme tak, jak jsme popsali na začátku. Teď už hlas každého člena započítáme pro libovolný řetězec maximálně jednou, takže program vydá správný výsledek. Zbývá se zamyslet nad složitostí.

Co je vlastně vstup? Kromě parametrů C, K a D to jsou zejména všechna oblíbená slova. Označme si počet všech znaků v nich jako ℓ.

Operace s trií, když máme konstantně velkou abecedu, můžeme bez obav prohlásit za konstantní. Do trie pro komisi přidáme maximálně ℓ znaků, čímž vytvoříme maximálně ℓ vrcholů. Při závěrečném průchodu navštívíme každý vrchol nanejvýš jednou, zpracování trie pro celou komisi tedy trvá O(ℓ) času a zabírá O(ℓ) paměti.

To samé platí pro trie jednotlivých členů. Zdánlivě tedy máme celkovou složitost O(C · ℓ). Jenže trie všech členů nemůžou mít dohromady víc než ℓ znaků, takže zpracování všech členských trií dohromady nemůže zabrat víc než O(ℓ).

Započítali jsme všechny operace? Skoro. Neměli bychom zapomenout na mocnění, ač ve vašich řešeních jsem jeho zohlednění nevyžadovala. Zatímco násobení za konstantní prohlásit můžeme, u mocnění by to bylo poněkud odvážné, zvlášť když by teoreticky mohlo nastat D ≫ ℓ. Trochu si ovšem život usnadníme a jen prohlásíme, že mocnění trvá O(m). Pak má celý náš program časovou složitost O(ℓ · m), paměťovou O(ℓ).

(Kdybychom se rozhodli slova nevkládat do trií, ale řadit, zvládneme to také lineárně – díky pevné velikosti abecedy to jde pomocí RadixSortu.)

Za zmínku možná stojí, že v téhle úloze občas realita spráská asymptotiku a pošle ji stydět se do kouta. I nepříliš optimalizovaná řešení se složitostí O(ℓ log ℓ) můžou pro rozumně velké vstupy doběhnout rychleji než řešení lineární. Souvisí to mimo jiné s tím, že trie je budovaná pomocí ukazatelů, a s efekty keší… ale to už by byl úplně jiný příběh.

Program (C)

Karolína „Karryanna“ Burešová

Teoretická úloha27-3-3 Výběr vysílačů (Zadání)

Úlohou je vlastně obarvit strom barvami 1, 2, 4, 8, … tak, aby sousední vrcholy měly různé barvy a součet hodnot barev přes všechny vrcholy byl co nejmenší. Připomeneme, že bez požadavku na minimální součet lze každý strom korektně obarvit dvěma barvami. To můžeme udělat například průchodem stromu do hloubky. Ten může vypadat například takto:

  1. obarvi(v, b):
  2. barva[v] = b
  3. for (u in soused(v)):
  4. if (barva[u]==0): obarvi(u, 3 - b)

Nejdříve obarvíme libovolný vrchol barvou 1, pak víme, že jeho sousedi musí mít barvu 2, jejich sousedi zase barvu 1, a tak dále. Tento jednoduchý algoritmus má časovou složitost O(N) a budeme na něm dále stavět.

Tím, že strom umíme obarvit barvami 1 a 2, dostáváme obarvení se součtem maximálně 2N. Tedy hledané obarvení s minimálním součtem určitě nepoužije barvy větší než 2N. To zároveň znamená, že barev použijeme maximálně log N + 1.

Nyní pomalu přejdeme k popisu algoritmu. Strom si zakořeníme v libovolném vrcholu a z něj pustíme prohledávání do hloubky. To vždy nejdříve spočítá řešení pro podstromy tvořené syny vrcholu a z těchto řešení složí řešení pro daný vrchol. Tento postup je takovým standardním dynamickým programováním na stromě. A co přesně v podstromech budeme počítat?

Pro každou barvu c = 2i pro i=1, … , log N + 1 spočítáme nejlepší možné obarvení podstromu, ve kterém je kořen obarven barvou c. Abychom zjistili nejlepší obarvení pro barvu c, tak stačí pro každého syna vybrat nejlepší barvu jinou než c. To pro konkrétního syna vždy bude buď jeho nejlepší barva, anebo jeho druhá nejlepší barva. Tudíž nám stačí si pro každý podstrom pamatovat pouze dvě nejlepší možnosti.

Po zavolání výpočtu v kořeni stromu dostaneme výsledek. Během výpočtu pro každý vrchol zkoušíme log N + 1 barev plus (log N + 1)-krát u něj vybíráme jednu ze dvou barev pro otce. Tedy časová složitost algoritmu je O(N log N). My ale algoritmus ještě vylepšíme.

Všimneme si, že pokud se má vyplatit vrcholu přiřadit barvu 2i, tak všechny barvy z 20, … , 2i-1 musí být zastoupeny v jeho synech. Tedy u vrcholu s k syny nám pro získání dvou nejlepších možností stačí vyzkoušet k + 2 barev (druhá nejlepší možnost pořád může mít barvu k + 2).

Další věc, kterou na předchozím algoritmu můžeme vylepšit, je opětovné vybírání z nejlepší a druhé nejlepší barvy synů. Víme, že vždy vybereme tu nejlepší kromě případu, kdy pro kořen zvolíme stejnou barvu, pak vybereme druhou nejlepší. Stačí nám spočítat součet nejlepších možností synů a pro každou barvu c=2i pro i=1, … , k+2 si předpočítat, o kolik se dohromady liší nejlepší a druhé nejlepší možnosti synů, kteří jako svou nejlepší barvu mají c. To pro vrchol s k syny můžeme jednoduše udělat v čase O(k).

Jelikož každý vrchol je synem právě (maximálně) jednoho jiného vrcholu, dostáváme se na časovou složitost O(N).

Pro zajímavost ještě řekneme, že stejný algoritmus funguje i pro verzi úlohy, kde strom barvíme barvami 1, 2, 3, … , N. Sami si můžete rozmyslet proč.

A kdo je zvědavý, tak strom, pro který jsou potřeba alespoň čtyři barvy, může vypadat například takto:

Příklad stromu potřebujícího čtyři barvy

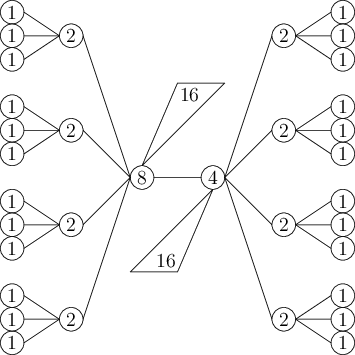
„Šestnáctkové“ trojúhelníky zastupují šestnáct přímých potomků uzlu, kde je každý obarvený jedničkou.

Karel Tesař

Praktická CodExová úloha27-3-4 Doplňování energie (Zadání)

První, co nás může napadnout, je vyzkoušet všechny možnosti průchodů. Těch je však velmi mnoho, protože nám nic nebrání chodit přes některá místa vícekrát.

Ujasněme si nejprve, jak bude vypadat přelet, který může získat maximální množství energie. Protože nemáme žádné omezení na uchovávanou energii, vyplatí se nám vždy při prvním navštívení nějakého místa z něj veškerou energii vyčerpat. Nemá tedy smysl si ji zde šetřit na později. Stejně tak je zbytečné nějaké místo při přeletu vynechat a nezastavovat se na něm.

Díky tomu můžeme předpokládat, že při každém čerpání energie máme projitou souvislou oblast, a navíc se nacházíme na jejím kraji. Tím jsme výrazně snížili počet možností, které chceme vyzkoušet. Nyní máme pouze N levých a N pravých konců, celkem N2 možných koncových stavů. Stav je tedy dvojice čísel (a, k), kde a je aktuální pozice a k druhý konec prošlé oblasti.

Jak ve stavech spočítat optimální množství energie? Pro stav s oběma konci intervalu na startovní pozici M energii určíme snadno. Bude rovna právě energii, kterou z této pozice můžeme čerpat.

Do ostatních stavů se můžeme dostat nejvýše ze dvou předchozích. Konkrétně pro a > k se do stavu (a, k) dostaneme ze stavu (a-1, k) nebo (k, a-1). A pro a < k to jsou stavy (a+1, k) a (k, a+1). Do nich se umíme dostat zase ze dvou předchozích, a tak dál. V každém případě můžeme začínat pouze ve stavu (M, M).

Stačí tedy z počátečního stavu procházet do šířky. Tím máme zaručeno, že projdeme všechny dosažitelné stavy a navíc je projdeme v tom pořadí, v jakém následují při průletu sondy. Můžeme tedy průběžně ve všech stavech počítat největší získatelné množství energie.

Při přechodu z (a, k) do (a+1, k) odebereme energii rovnou vzdálenosti mezi místy a a a+1. Pokud však přecházíme přes prošlou oblast, tedy například z (a, k) do (k-1, a), musíme odečíst i součet vzdáleností mezi všemi již prošlými místy. Nakonec nesmíme zapomenout přidat energii získanou na nové pozici.

Celý průchod je nakonec velmi jednoduchý, jenom se nesmíme ztratit v indexování a přičítání ±1. Na detaily se podívejte do zdrojového kódu. Časová složitost celého algoritmu je O(N2), protože každý z kvadraticky mnoha stavů zkoušíme nejvýše jednou. Díky tomu, že nepotřebujeme optimální cestu sondy zrekonstruovat, vystačíme si s lineární pamětí.

Program (C)

Jenda Hadrava

Praktická opendata úloha27-3-5 Komprese obrazu (Zadání)

Protože na vstupu dostaneme vždy obrázek o rozměrech 2K×2K, v každé úrovni rekurzivního komprimování pracujeme vždy se čtvercem. Pokud má na aktuální úrovni čtverec rozměry 1×1, nic již nekomprimujeme a jen vrátíme jeho barvu.

Co přesně máme v každém kroku kvadrantistické komprese dělat? Potřebujeme vybrat dvě čtvrtiny uvažovaného čtverce a každou „odbýt“ jednou barvou, respektive jednu prohlásit za celobílou a druhou za celočernou. Řekněme, že cenou výsledné komprese je počet pixelů, které musely být přebarveny.

To nás může svádět k řešení, ve kterém pro každou čtvrtinu spočteme počet černých a bílých pixelů. Následně „nejčernější“ z nich obarvíme černě, nejbělejší bíle a zbylé čtvrtiny pak zpracujeme rekurzivně, přičemž rekurzivní funkce bude vracet cenu zakomprimování dané části. Toto řešení má dva problémy – jednak není úplně jasné, jak vybírat nejbělejší a nejčernější čtvrtiny (může jich být více se stejným počtem bílých/černých pixelů), a navíc nemusí vést k optimálnímu řešení.

Mohlo by se totiž stát, že sice v jedné čtvrtině je hodně černých pixelů, více než v ostatních, ale díky rozložení černých pixelů se dobře kvadrantisticky komprimuje. Pak by jí tento algoritmus obarvil celočerně a namísto toho se kvadrantisticky snažil komprimovat čtvrtinu, která má pixely rozložené dost nepravidelně.

Zkusme to trochu jinak – na každé úrovni se pro každou čtvrtinu zeptáme naší rekurzivní funkce, kolik by stálo její zkomprimování. Budeme si pamatovat i počet černých a bílých pixelů v každé čtvrtině. Pokud známe tyto informace, můžeme prostě vyzkoušet všech 12 možností, jak vybrat celočernou a celobílou čtvrtinu, a seskládat pro každou z možností její cenu. Ze všech dvanácti cen si pak vybereme tu nejmenší.

Kolik na takový výpočet potřebujeme času? Povšimněme si, že rekurzivní funkce se nikdy nevolá znovu pro stejný čtverec, protože uvažované čtverce stejné velikosti se nikde nepřekrývají. Víme, že na každém čtverci velikosti 2m×2m strávíme O(4m) času, a takových čtverců uvažujeme na každé úrovni rekurze
4K
4m
. Celkem tedy potřebujeme O(4K  · K) času i paměti.

Toto řešení by šlo ještě zrychlit: určit počet bílých pixelů pro každý čtverec lze v čase O(1), protože stačí sečíst výsledky ze čtyř menších čtvrtin. A pokud si vybrané „odbyté“ čtvrtiny budeme uchovávat trochu lépe, dostaneme řešení, které si vystačí s lineárním časem i pamětí v počtu pixelů.

Program (C++)

Ondřej Hübsch

Teoretická úloha27-3-6 Ukládání přepravek (Zadání)

Někteří z vás poznali, že jde jen o jiné zadání daleko známější úlohy, totiž barvení intervalových grafů. Tato úloha se dá ve zkratce zadat jako hledání nejmenšího počtu poslucháren, které potřebujeme pro přednášky zadané svými časy začátků a konců.

Tato úloha se dá řešit hladově, a to ve velkém množství variant, proto byla většina řešení funkční. Hlavní část řešení je ovšem obhájit, že hladově řešit opravdu jde.

Začneme tím, že si přepravky seřadíme podle vnějšího průměru sestupně. Na vnitřním průměru tady nezáleží, jak později uvidíme. Budeme si udržovat seznam potřebných komínků, jakési průběžné řešení. Jediná hodnota, kterou z každého komínku potřebujeme, je vnitřní průměr nejmenší přepravky.

Přepravky budeme postupně probírat a snažit se je vložit do nějakého komínku. Protože víme, že žádná větší přepravka už nepřijde, stačí ze seznamu vybrat maximum. Bude se nám tedy hodit reprezentovat komínky maximovou haldou.

Pokud je maximum menší než vnější průměr aktuální přepravky, pak žádný vhodný komínek neexistuje a proto přidáme nový. Na konci běhu algoritmu prostě jen spočítáme počet komínků ve stromu.

Konečnost algoritmu je zřejmá, podívejme se na správnost. Dokážeme ji indukcí podle velikosti průběžného řešení. Dokud máme jen jeden komínek (případně žádný), nemůže existovat lepší řešení.

Mějme tedy k komínků. Jediné, co může k zvýšit, je pak situace, kdy neexistuje pro nějakou přepravku vhodný komínek. V tu chvíli ale existuje alespoň k přepravek, co mají vnější průměr alespoň takový jako aktuální přepravka (díky setřízení), a vnitřní průměr ostře menší (neexistuje vhodný komínek). S aktuální přepravkou je to tedy k+1 přepravek, ze kterých žádné dvě nejdou vložit do sebe. Optimální řešení tedy nemůže používat méně než k+1 komínků.

Jaké vlastnosti algoritmus má? Už kvůli prvotnímu setřízení vidíme, že nepoběží rychleji než v O(N log N). Další kroky algoritmu závisí na počtu komínků, tedy na řešení. Ten nemůžeme nijak rozumně odhadnout – počet komínků může být až N. Každý krok tedy zabere až O(log N) času. Tedy nakonec se opravdu do O(N log N) vejdeme. Paměti spotřebujeme O(N), více nepotřebujeme.

Vzorový kód je napsaný v C++ a využívá standardní implementaci haldy.

Program (C++)

Ondra Hlavatý

Seriálová úloha27-3-7 UNIXové déjà vu (Zadání)

S třetím dílem seriálu o UNIXu jste se poprali statečně. Nejvíc zádrhelů bylo paradoxně v nejméně hodnoceném prvním úkolu, jehož vzorové řešení si necháme až na konec, abyste se nelekli a neutekli hned na začátku. Trochu jste také zápasili se skriptovacími úkoly, kde se projevily jednak nedostatek zkušeností s efektivním kombinováním shellových utilit, jednak znalosti získané jinde. Ty některým z vás dovolily napsat neportabilní kód, který by v jiném shellu než Bashi neběžel. Používejte shell častěji, zkuste si s jeho pomocí šetřit práci, hrajte si s ním. Stručné, elegantní a efektivní vyjadřování vám v něm pak půjde snáz a nebude vás to tolik svádět k používání céčkových konstrukcí v shellu.

Úkol 2 – Hardlinky na adresáře

Pohledem do man ls nebo do předchozího dílu seriálu můžeme zjistit, že ls -ld adresar vypíše podrobnosti o daném adresáři, nikoliv o souborech v něm umístěných, jako by to udělal bez přepínače -d. Počet linků je první číslo vpravo od práv. Experimentální pozorování na všech slušných systémech prozradí, že toto číslo je vždycky aspoň 2. Porovnáváním adresářů s nízkým a vysokým počtem linků přijdeme na to, že se o jedničku zvětší za každý podadresář. Po troše přemýšlení a přečtení výkladu v seriálu by mělo být jasné, že jeden link vede z nadřazeného adresáře, druhý z adresáře samotného (jmenuje se . – tečka) a zbytek jsou dvě tečky (..) z podadresářů.

Mezi slušné systémy tu nemůžeme počítat Cygwin, který o každém adresáři tvrdí, že má jediný link. Tečku a dvě tečky implementuje úplně speciálně, a to hlavně kvůli podpoře windowsových souborových systémů. Při hlubším pohledu do POSIXu jsem s podivem zjistil, že norma takové chování dovoluje – konkrétně v definici prázdného adresáře.

Tenhle úkol se ukázal být celkem jednoduchým na slušných i neslušných systémech.

Úkol 3 – Mazání obsahu a linku

Příkaz cat </dev/null >soubor zkrátí délku souboru na nulu. Pokud před jeho zavoláním soubor smažeme příkazem rm (té operaci se říká také unlink – maže se jenom jeden link), původní data se nemění a vytvoří se nový prázdný soubor. Důsledkem je, že původní data jsou pořád přístupná přes zbývající linky, pokud nějaké existují. Pokud se soubor předem neunlinkuje, přepíše se původní obsah a změna se projeví při přístupu přes libovolný link.

Na tomto místě bychom rádi připomněli, že inode je datová struktura, která si pamatuje metadata souboru a odkazy na jeho datové bloky. Link ukazuje na inode. Je to záznam v adresáři, který má jméno (jméno souboru) a číslo inode souboru. Data adresáře se vlastně skládají jen z takových záznamů. V těchto pojmech jste měli v řešení dost zmatku.

Úkol 4 – Nuceně privátní home

Při klasickém umístění domovských adresářů, tedy v /home/<uživatel>, je úloha představenými prostředky neřešitelná. Vlastník souboru totiž vždycky může měnit jeho práva, takže bychom museli buď měnit práva adresáři home a odstřihnout tak přístup do vlastních domovských adresářů ostatním uživatelům, nebo používat nějaký speciální mechanismus. Norma POSIX ale žádný neposkytuje, jen na souborovém systému ext2 (a vyšších) jste objevili příkaz chattr, který si dovolím ignorovat jako těžce neportabilní.

Nemusíme se ale tak moc omezovat, v /etc/passwd je možné cestu k domovskému adresáři nastavit. To je dobré vědět, abyste se nikdy na klasické umístění domovského adresáře nespoléhali a vždycky ve skriptech používali expanzi vlnky (~, ~hroch, …) nebo obsah proměnné prostředí HOME ($HOME expanduje na cestu k domovskému adresáři aktuálního uživatele).

Potřebný nápad je použití nadřazeného adresáře pro kontrolu přístupu. Root si může přivlastnit adresář nadřazený domovskému adresáři hrocha, sebrat práva světu (others), jako skupinového vlastníka nastavit skupinu obsahující jen hrocha a této skupině dát právo k prohledávání (x). Nikdo jiný než root a hroch tak nemá možnost se k hrochovu domovskému adresáři dostat, ať se snaží sebevíc.

Budeme tedy potřebovat skupinu, ve které je hroch sám. Často taková skupina již existuje a jmenuje se hroch. Pokud neexistuje, snadno ji vytvoříme:

groupadd hroch
usermod -aG hroch hroch

Teď už jen vytvořit „neprůhledný“ adresář a přesunout do něj hrochův stávající domovský adresář:

usermod -md /home/hroch_priv/hroch hroch
chown root:hroch /home/hroch_priv
chmod 750 /home/hroch_priv

Úkol 5 – Preprocessing

Od pohledu chceme použít jeden cyklus přes řádky a jeden cyklus přes tokeny na řádku. Když na řádku najdeme token COMMENT, zahodíme všechno až do konce řádku – tomu odpovídá příkaz break ve vnitřním cyklu. Token BYE odpovídá volání return – funkce v ten okamžik má skončit a víc ze vstupu nečíst.

Budeme číst zdrojáky, takže se nám bude hodit přepínač -r příkazu read. Jinak by zpětná lomítka dělala neplechu.

Při volání funkce se hodí možnost mít lokální proměnné. Třeba když měníme proměnnou IFS, není pěkné ji nechat změněnou po návratu z funkce, jiné kusy kódu se pak mohou chovat neočekávaně. POSIX v tomto ohledu nabízí dvě řešení, obě dost špatná.

Bash nabízí třetí řešení, které jiné shelly nemají. Tím je vestavěný příkaz local, o kterém se více dozvíte v help local. Používá se podobně jako export a příklad použití najdete ve vzorovém řešení.

Už ve druhém dílu seriálu jste potkali konstrukce for, case a podmínky. Podmínky jste se učili i pomocí ||. Přidejme k tomu obsah třetího dílu a řešení je na světě.

Program (shell)

Zvolil jsem nejjednodušší realizaci smyčky přes tokeny. Nechal jsem shell pomocí IFS rozdělit řádku vstupu podle mezer a přes výslednou množinu slov jsem pustil for-cyklus. Ve složitějším programu by bylo nepříjemné, že se ve smyčce nejde rozumně podívat na tokeny před a za aktuálně zpracovávaným. To by se dalo napravit použitím jiné smyčky. Příkaz read může opakovaně odkousávat první token; smyčka se zastaví, když zbytek řádku ke zpracování už je prázdný.

while [ -n "$line" ]; do
	IFS=' ' read -r token line <<EOF
$line
EOF
	# tělo cyklu
done

Tuto syntaktickou vlastnost shellu možná vidíte poprvé. Slovo <<EOF je přesměrování vstupu. Vstup se bere z následujících řádek, až do slova EOF, které je úplně samo na řádku (nesmí předcházet ani bílé znaky!). Říká se tomu here document. Místo EOF je možné použít i jiný řetězec. Na začátku (za <<) může být v uvozovkách, v tom případě může obsahovat i mezery, na konci je ale vždycky bez uvozovek. Při použití jednoduchých uvozovek (<<'EOF') se celý here document chová jako řetězec v jednoduchých uvozovkách, tedy se v něm neexpandují proměnné ani se neprovádí substituce příkazů.

Kdybychom se chtěli použití here document vyhnout, jde to, ale není to pěkné:

r() { IFS=' ' read -r token line; }
token="$(echo "$line" | { r; echo "$token"; })"
line="$(echo "$line" | { r; echo "$line"; })"

Opět si uvědomte, co se stane při vynechání složených závorek, co je za zádrhel s readem v pipeline, jak se v pipeline chová exit.

Trochu potíží nadělá ještě vynechávání prázdných řádků. Projděte si vzorový kód a rozmyslete si, že a jak funguje. Všimněte si použití podmínek a příkazů true a false. Podotýkám, že pro vypsání stringu bez konce řádku na echo -n všude spoléhat nejde. Příkaz printf je portabilní, chová se předvídatelně a POSIX ho doporučuje používat místo echo.

Úkol 6 – Ztabulkování /etc/passwd

O formátu /etc/passwd jste si měli přečíst v man 5 passwd nebo analogickém zdroji. Pomocí standardních prostředků si s úlohou můžete snadno poradit za použití while, read, IFS a printf.

Použití tabulátorů jako oddělovačů sloupců nestačí, protože pak se tabulka rozpadne, když se liší délky položek jednoho sloupce po vydělení osmi (rozestup tabulačních zarážek). Předpokládal jsem, že si víc přečtete o printf a jeho formátovacích direktivách, jak napovídalo i umístění úlohy. Najít jste potřebovali nastavení šířky, na jakou se string má doplnit mezerami. Na plný počet bodů stačilo maximální délku položky v každém sloupci odhadnout konstantou, obludně dlouhý login klidně smí tabulku rozbít. Šlo by šířku sloupců i počítat, ale to za druhý průchod souborem a dost kódu navíc nestojí.

tplt='%-13s\t%-1s\t%5s\t%5s\t%-35s\t%-25s\t%s\n'
while IFS=: read login passwd uid \
	gid name home shell; do
	printf "$tplt" \
		"$login" \
		"$passwd" \
		"$uid" \
		"$gid" \
		"$name" \
		"$home" \
		"$shell"
done < /etc/passwd

Backslash na konci řádku dovolí v příkazu pokračovat na dalším řádku a logický řádek tak fyzicky rozdělit. Nesmí za ním být do konce řádku už nic jiného, ani bílé znaky.

Vzorové řešení už znáte, ale zmíním ještě řešení, kterým jste mě překvapili. Není portabilní, zato na úlohu padne jako ulité a za celkem rozšířené se rozhodně dá považovat. Je jím příkaz column, který slouží k výpisu dat do tabulky. Bez parametrů považuje vstup za seznam jednotlivých položek a řádek může ukončit mezi libovolnými dvěma z nich, s přepínačem -t respektuje řádkové zlomy ve vstupu a může nechávat v tabulce na koncích řádků prázdné buňky. Přepínač -s nastavuje oddělovač sloupců na vstupu a -n zakazuje ignorování prázdných buněk.

column -t -s: -n /etc/passwd

Úkol 1 – Velikosti bloků

Jako poslední nám zbývá první úkol. Zadání se nepodařilo zformulovat tak, abyste se ho nesnažili řešit cestami, které vás protáhnou detaily současných disků. Seriál tím směrem nemířil, ale cestu do pekel si mnozí z vás našli sami.

Jak jsem doufal, že k řešení přistoupíte? Já bych si zakládal soubory různých velikostí a zkoumal na nich výstup příkazu du s přepínačem -h a bez něj. Vyrobit takový soubor velikosti N bytů můžeme třeba příkazem head -c N /dev/zero > soubor, jak bylo ukázáno v textu seriálu.

Pokud tedy nemáme zapnutý inlining, o kterém jsem také psal, vlastně stačí soubor velikosti 1: echo > soubor. Ten určitě bude zabírat nejmenší možné nenulové množství paměti, tj. jeden diskový blok. (Prázdný soubor by často zabral jen inode, který se do počtu zabraných bloků nepočítá.) S inliningem by bylo potřeba soubor postupně zvětšovat a někde ve větších velikostech hledat velikost, při které přidání jediného bytu zvětší počet bloků zabraných souborem. Pak by stačilo odečíst velikost před zvětšením.

Příkaz du -h soubor nebo lépe du -B 1 soubor nám ukáže, jak velký takový blok je. Když použijeme du soubor bez přepínačů, dozvíme se, kolik bloků soubor podle představ utility du zabírá, z čehož už snadno dopočítáme, jak velký blok utilita používá.

Na Linuxu to bývá 1024 B. Ovšem když nastavíme proměnnou prostředí POSIXLY_CORRECT (na libovolnou hodnotu), du se přizpůsobí požadavkům POSIXu a začne používat bloky o velikosti 512 B. Není bez zajímavosti, že tato proměnná mívala alias POSIX_ME_HARDER, což ilustruje názor autorů na některé části normy. Zajímavé čtení o této proměnné najdete na stránce Waikatské skupiny uživatelů Linuxu.

Utilita ls tu vůbec nebyla potřeba. Spousta z vás se snažila využít její přepínač -s a zjišťovala tak velikost bloku používaného utilitou ls namísto toho používaného utilitou du.

Kdybychom chtěli vyloučit i možnost obskurní velikosti bloku, která není mocninou dvojky, můžeme pozorovat stejným způsobem velký soubor známé velikosti. Ve velkém počtu bloků by se i jedničkový rozdíl nasčítal, takže by počet bloků neseděl přesně.

Doplníme, že jeden diskový blok často mívá velikost 4 kB. Poučení z úlohy mělo být, že reálná velikost diskového bloku a velikost bloku používaná utilitami spolu nemají nic společného. Není blok jako blok.

Jenže se to zkomplikovalo, když jste začali hledat a používat utility, které nepracují s diskem přes souborový systém, ale koukají na něj přímo. A tak se přestaňme schovávat za představu ideálního světa, kde existuje něco jako diskový blok, a povězme si, jak se to s bloky na disku má doopravdy.

Bloků existuje víc různých typů, konkrétně jste narazili na tři. Fyzický sektor, logický sektor a alokační jednotka (neboli cluster). Nakonec jako bonus přidám ještě IO blok.

Začněme od nejnižších vrstev abstrakce, u fyzického sektoru. To je blok, který interně používá pevný disk a jeho firmware. Vůbec by nás jako uživatele nemusel zajímat, kdyby jeho velikost nesouvisela s výkonem programů, které s diskem intenzivněji pracují. U starších disků má velikost 512 B, u novějších (od roku 2011) 4096 B. Formátu novějších sektorů se říká Advanced Format (AF) – pod tímto termínem vygooglíte víc.

O vrstvu abstrakce výš leží logický sektor. V nich disk přemýšlí, když komunikuje se zbytkem počítače, typicky přes svůj ovladač v operačním systému. U starších disků se nelišil od fyzického, AF podle něj definuje dvě kategorie zařízení. První je 512e (e jako emulace) s 512B logickým sektorem, druhá 4Kn (n jako nativní) s 4096B logickým sektorem. Kategorie 512e se snaží být aspoň navenek zpětně kompatibilní, uvnitř už ale vyzvedává a ukládá celé 4kB fyzické sektory.

Teprve nad ovladačem disku sedí souborový systém a diskový prostor dělí na alokační jednotky, čili clustery. Po takových blocích přiděluje paměť jednotlivým souborům, a právě na ně se snažil první úkol seriálu mířit. Velikost alokační jednotky už není zadrátovaná v hardware, bývá možné ji nastavit při vytváření souborového systému, ale zejména kvůli efektivitě se obvykle volí jako celočíselný násobek velikosti sektoru.

Pro úplnost uvedeme ještě čtvrtý typ bloku, na který jste už nenarazili. Operační systém má nějaké povědomí o tom, jak by se na disk mělo přistupovat, s jak velkými bloky by se ideálně mělo pracovat najednou. Říká se jim IO bloky (I je input, O output). Dosud jsme psali především o klasických pevných discích. Pro ně mívají stejnou velikost jako alokační jednotka souborového systému, vnitřní struktura SSD disků ale vyžaduje IO bloky zpravidla mnohem větší, aby se zbytečně nepřepisovaly velké kusy paměti a nezkracovala se tak životnost zařízení. Program intenzivněji pracující s diskem si pak může přečíst, po jakých blocích je dobré číst, nebo si to může nechat nadiktovat od uživatele, jako to dělá třeba utilita dd pro čtení a zápis po blocích. Je prastará a na nestandardní syntaxi jejích parametrů je to vidět, nenechte se vyděsit. :-)

Když se začnete vrtat ve specifikách jednotlivých souborových systémů, najdete džungli specialit, na které běžně ve svém počítači nenarazíte. Více detailů si v zájmu zachování vašeho duševního zdraví dovolíme nerozebírat. Pokud si ho nevážíte, koukněte na pojmy block suballocation, sparse file, inlining nebo na souborový systém jménem ZFS.

Další debatu s vámi rád povedu na fóru, ať už se bude týkat vašich řešení, tohoto textu, UNIXu nebo disků a souborových systémů.

Samé příjemné zážitky s UNIXem přeje

Tomáš „Palec“ Maleček