Recepty z programátorské kuchařky
Binární vyhledávání
Aktuální verze kuchařky: prosinec 2017
Binární vyhledávání je mocná technika, která se objevuje ve všemožných algoritmech a úlohách. Obecně spočívá ve využívání monotónnosti nějakého pole nebo funkce k rychlejšímu prohledávání. To zní pravděpodobně velmi nejasně; začneme proto konkrétnějšími příklady a budeme postupně zobecňovat.
Ve své nejjednodušší podobě je binární vyhledávání technika, která nám umožní rychle prohledávat seřazené pole. Řekněme, že máme vzestupně setříděné pole A, o kterém víme, že obsahuje číslo k. Chceme zjistit, jaký má k index v poli, čili pro jaké i platí A[i] = k. Budeme v podstatě hádat, který index to je, a zpřesňovat náš odhad. Napřed odhadneme index v polovině pole (ten označíme mid jako middle, čili střed).
- Pokud A[mid] = k, je hotovo.
- Pokud A[mid] < k, všechny prvky A nalevo od mid musí být také menší než k. Proto vyhledávání spustíme znovu, ale pouze na prvcích napravo od mid (samozřejmě už bez mid).
- Pokud A[mid] > k, analogicky spustíme vyhledávání na levé polovině.
Pokud pole nemá přesný střed (má sudou délku), zvolíme za mid a libovolný ze dvou prostředních indexů.
Řekněme například, že chceme v poli [1, 4, 5, 7, 11, 16, 20] zjistit index čísla 11. Vyhledávání bude postupovat takto:
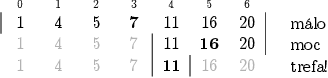
Výsledek je tedy 4. Stačilo nám podívat se na tři prvky, takže výrazně méně než 7 v naivním prohledávání.
Protože délka intervalu, na kterém hledáme, se v každé iteraci zmenší alespoň na polovinu, po i-té iteraci bude mít interval délku nejvýše N / 2i (kde N je délka pole). Celkem proto provedeme maximálně log2 N iterací, než se dostaneme na délku 1. Časová složitost je proto O(log N).
Nejintuitivnější je asi rekurzivní představa, která v kódu vypadá takto:
int A[n]; // dané pole
// Vyhledávání čísla k, pokud víme, že se
// nachází někde v intervalu <l, r>.
// Při použití voláme indexPrvku(0, n-1, k),
// abychom prohledávali celé pole.
int indexPrvku(int l, int r, int k) {
if (l > r) // voláme se na prázdný úsek
return -1; // zde hledané k určitě není
int mid = (l + r) / 2; // průměr hranic
if (A[mid] == k) { // hotovo
return mid; // mid je hledaný index
} else if (A[mid] < k) { // chceme víc
// spusť na pravé půlce (ale už bez mid)
return indexPrvku(mid + 1, r, k);
} else { // poslední možnost: chceme méně
// spusť na levé polovině
return indexPrvku(l, mid - 1, k);
}
}
# pole A je dané
# Vyhledávání čísla k, pokud víme, že se
# nachází někde v intervalu <l, r>.
def index_prvku(l, r, k):
if l > r: # voláme se na prázdný úsek
return None # zde hledané k určitě není
mid = (l + r) // 2 # průměr hranic
if A[mid] == k: # hotovo,
return mid # mid je hledaný index
elif A[mid] < k: # chceme víc
# spusť na pravé půlce (ale už bez mid)
return index_prvku(mid + 1, r, k)
else: # poslední možnost: chceme méně
# spusť na levé polovině
return index_prvku(l, mid - 1, k)
# Zavoláme na <0, len(A) - 1>, tedy na celé pole
index = index_prvku(0, len(A) - 1, k)
if index is None:
print("{} se v poli nevyskytuje.".format(k))
else:
print("{} se v poli vyskytuje na pozici {}"
.format(k, index))
Může se nám stát, že hledané k v poli neleží. To při vyhledávání poznáme tak, že se nám interval, kde k ještě může být, zmenší na prázdný. Komentáře kód značně prodlužují, ale v praxi je to opravdu jen pár řádků. Častěji se však používá implementace, kde místo rekurze použijeme cyklus. Převod je jednoduchý, uvedeme si tedy i tuto verzi:
int A[n]; // dané pole
int indexPrvku(int k, int n) {
// Po celou dobu platí, že k se musí
// nacházet někde v intervalu <l, r>.
int l = 0, r = n - 1;
while (l <= r) {
// dokud je interval <l, r> neprázdný
int mid = (l + r) / 2;
if (A[mid] == k) {
return mid;
} else if (A[mid] < k) {
l = mid + 1;
} else {
r = mid - 1;
}
}
return -1;
// Pole neobsahuje k,
// jinak bychom ho už našli.
}
# Pole A je dané
def index_prvku(k):
# po celou dobu platí, že k se musí
# nacházet někde v intervalu <l, r>
l, r = 0, len(A) - 1
while l <= r:
# dokud je interval <l, r> neprázdný
mid = (l + r) // 2
if A[mid] == k:
return mid
elif A[mid] < k:
l = mid + 1
else:
r = mid - 1
return None
# Pole neobsahuje k,
# jinak bychom ho už našli
Binární vyhledávání přes funkce
Uvažme, jak by se kód změnil, kdybychom pole A neměli uložené v paměti, ale načítali bychom ho například z disku nebo po síti. Pak bychom nejspíš měli nějakou funkci f, které bychom se mohli ptát na jednotlivé indexy a ona by nám vracela příslušné hodnoty. Jediná změna by pak byla v tom, že bychom se místo přistupování k prvkům pole ptali této funkce na odpovídající indexy.
Binární vyhledávání je totiž mnohem mocnější než prosté vyhledávání v poli. Naše funkce pro binární vyhledávání nyní vlastně nepracuje s žádným polem, jen s nějakou funkcí f. Za tu ale můžeme dosadit něco úplně jiného než jen prvky pole. Musíme však dodržet vlastnost, že f je neklesající, aby mohlo vyhledávání fungovat (stejně tak by mohla být nerostoucí, ale tento připad je analogický, takže se budeme zabývat pouze neklesajícími funkcemi).
Zkusíme tedy za f dosadit něco jiného. Řekněme, že chceme pomocí binárního vyhledávání umět počítat třeba druhou odmocninu čísla: máme dané číslo x a chceme najít číslo mid ≥ 0 takové, že mid je odmocnina z x. Jinak řečeno, mid2 = x. Binárním vyhledáváním úlohu vyřešíme tak, že budeme hádat čísla mid a vždy srovnáme f(mid) = mid2 s x. Pokud je mid2 větší než x, mid je větší, než chceme. Horní hranici proto nastavíme na toto mid. A naopak, pokud je mid2 menší, nastavíme spodní hranici na toto mid. Důležité je, že pro kladná mid je funkce f neklesající, jinak bychom na ní binárně vyhledávat nemohli.
Na obrázku je případ, kdy hledáme odmocninu ze dvou. V první iteraci jsme mid odhadli na 1 a f(mid) je proto taky 1, takže méně než x (které je 2). Zahodíme proto levou polovinu.
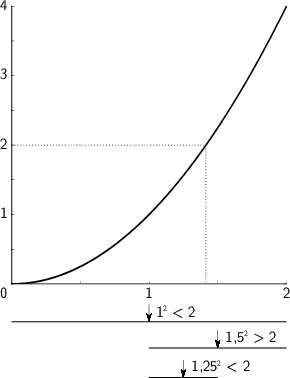
Protože odmocnina může být iracionální, nemůžeme předpokládat, že ji dokážeme spočítat přesně, tzn. že by nastal případ mid2 = x. Odmocninu tedy jen aproximujeme. Pro takovéto aproximační úlohy stačí cyklus zopakovat dostatečněkrát, abychom získali rozumnou přesnost. Přesnost se velmi rychle zvyšuje (s každou iterací se velikost intervalu, kde se může nacházet výsledek, zmenší na polovinu), a proto většinou stačí třeba 100 iterací.
Drobný, ale podstatný detail je volba intervalu ⟨ℓ, r⟩, ve kterém vyhledávání začínáme – pokud hledané mid leží mimo tento interval (tj. neplatí, že f(ℓ) ≤ f(mid) ≤ f(r)), algoritmus samozřejmě nemůže fungovat. Pro náš příklad s f(x) = x2 jsme zvolili ℓ= 0, r = max(1, x), rozmyslete si, proč tato volba funguje.
V kódu:
double f(double a) {
return a * a;
}
double odmocnina(double x) {
double l = 0, r = max(x, 1);
for (int it = 0; it < 100; it++) {
double mid = (l + r) / 2;
if (f(mid) < x) l = mid; // chceme víc
else r = mid; // chceme míň
}
return l;
// l a r jsou dostatečně blízko,
// je jedno, ktere vrátíme
}
def f(a):
return a * a
def odmocnina(x):
l, r = 0., max(float(x), 1.)
for iterace in range(100):
mid = (l + r) / 2
if f(mid) < x: l = mid # chceme víc
else: r = mid # chceme míň
return l
# l a r jsou dostatečně blízko,
# je jedno, které vrátíme
Kód je velmi podobný předchozímu, přestože dělá něco docela jiného. Oproti
minule nepracujeme s celými čísly, ale s čísly reálnými. Z toho plynou změny,
které jsme vysvětlili výše. Případ f(mid) == x přeskakujeme proto, že chceme
jen dostatečně dobrý odhad a v naprosto přesný výsledek nedoufáme.
Funkce f je nyní úplně jiná než předtím, ale vyhledávání funguje analogicky. Důležité je, že hodnotu f zjišťujeme tolikrát, kolik proběhne iterací cyklu (zde stokrát, v celočíselném případě O(log N)-krát), takže jen málokrát. Její výpočet tak může být i poměrně pomalý a celý program poběží pořád rychle – samozřejmě jen v porovnání s tím, kdybychom si počítali všechny funkční hodnoty; bude-li nás výpočet jedné hodnoty stát třeba O(2N) času, ani binární vyhledávání nás nespasí.
Jak se vypořádat se stejnými hodnotami
Přesuňme se zpět do celých čísel. Hned v příkladu s vyhledáváním v poli jsme opomenuli případ, kdy se nějaké číslo v poli vyskytuje víckrát. V takových případech chceme zpravidla najít první nebo poslední pozici prvku. Takto můžeme například najít v seřazeném poli poslední prvek, který má hodnotu maximálně k. Pokusme se k tomuto účelu binární vyhledávání upravit.
Existuje několik způsobů, jak se s tím vypořádat, ale často bývají náchylné na chyby, zejména na plus-minus-jedničkové. Nejjednodušší je pamatovat si nejvyšší index pole, který podmínku splňuje, a ve vyhledávání pokračovat jako obvykle, dokud se nám interval nezmenší na nulový nebo záporný. Může to vypadat takto:
int A[n]; // dané pole
bool neniVetsiNezK(int x, int k) {
// není větší než k, takže je možným řešením
return A[x] <= k;
}
int nejvetsiPrvekNeVetsiNezK(int n, int k) {
int l = 0, r = n - 1;
int nejlepsi = -1;
while (l <= r) {
// dokud není interval prázdný
int mid = (l + r) / 2;
if (neniVetsiNezK(mid, k)) {
nejlepsi = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return nejlepsi;
// Pokud žádný prvek nesplňuje podmínku,
// vrátí se -1
}
# pole A je dané
def neni_vetsi_nez_k(x, k):
# není větší než k, takže je možným řešením
return A[x] <= k
def nejvetsi_prvek_ne_vetsi_nez_k(k):
l, r = 0, len(A) - 1
nejlepsi = None
while l <= r:
# dokud není interval prázdný
mid = (l + r) // 2
if neni_vetsi_nez_k(mid, k):
nejlepsi = mid
l = mid + 1
else:
r = mid - 1
return nejlepsi
# Pokud žádný prvek nesplňuje podmínku,
# vrátí se None
Všimněme si, že když najdeme prvek, který podmínku splňuje, zmenšíme interval
na pravou polovinu. To znamená, že když pak najdeme další prvek, který také
podmínku splňuje, bude nutně lepší. Proto můžeme nejlepsi nastavit rovnou
na mid bez jakýchkoli srovnání.
Vyhledávání podle predikátu
Schválně používáme frázi „prvek, který splňuje podmínku“ místo něčeho jako
„prvek, který není větší než k“. Můžeme totiž udělat další abstrakci –
při vyhledávání nám nezáleží na porovnávání nějakých čísel, jen na tom, jestli
prostřední hodnota splňuje nějakou podmínku, čili predikát. Důležité je, že tento
predikát je „nerostoucí“, čili na začátku je na nějakém úseku vždy splněný
(vrátí true) a dále už nikdy. My hledáme právě hranici mezi těmito částmi:
nejvyšší hodnotu, pro kterou funkce vrátí true.
Formálně, predikát p(x) musí splňovat:
false ⇒ (y >
x ⇒ p(y) = false).To znamená, že když někde predikát není splněn, dále už nebude splněn nikde.
Predikát je v tomto případě f(mid) >= hledany, ale klidně by to mohlo
být něco jako „je možné vyskládat x koní na šachovnici tak, aby se
neohrožovali?“ Tímto způsobem můžeme řešit úlohy typu „najděte největší k,
pro které ještě platí podmínka“. Někdy se totiž stává, že původní problém není
možné jednoduše zodpovědět, ale dokážeme rychle (řekněme v O(N) nebo O(N
log N)) odpovědět na dotazy typu: „Platí ještě pro dané k podmínka?“ Pak
stačí implementovat tyto dotazy a binární vyhledávání nám dá odpověď. Například
úlohu „Kolik nejvíce koní je možné umístit na šachovnici tak, aby se
neohrožovali?“ můžeme redukovat na „Je možné vyskládat x koní na
šachovnici tak, aby se neohrožovali?“ za použití binárního vyhledávání.
Uveďme příklad (zjednodušení P-I-1 z MO-P 2015): Máme hotel, který má N (max. 106) pater. V každém patře je jeden pokoj. Postupně se do hotelů ubytovává H hostů (H ≤ N), z nichž i-tý může být ubytován maximálně v patře ai (protože se bojí výšek). Kolik hostů dokážeme ubytovat, než budeme muset nějakého odmítnout, protože se nikam nevejde?
Řešení: Dokážeme jednoduše zjistit, zda dokážeme ubytovat prvních K hostů. Stačí vzít prvních K, tuto posloupnost seřadit a pak zabírat patra odspoda – host s největším strachem z výšek do prvního patra a tak dále. To zabere O(N log N) času. S touto podmínkou už spustíme binární vyhledávání a dostaneme odpověď za O(N log 2 N) času.
Ne vždy je predikátová forma úlohy jednodušší než původní úloha, třeba při hledání nejkratší cesty nedokážeme rychle zjistit, zda existuje cesta dlouhá maximálně x. Vždy je ale dobré se zamyslet, zda by binární vyhledávání mohlo pomoci.
Příklady
Papír
(Těžší verze této úlohy byla zadána jako úloha D na ACM ICPC World Finals 2015.)
Máme obdélníkový papír, ve kterém jsou vystřihnuté díry ve tvaru kruhu. Všechny díry jsou celé uvnitř papíru a nepřekrývají se. Kde máme vést řez papírem rovnoběžný s osou x tak, aby byl papír rozdělen na dvě části o stejném obsahu? Děr může být až 100 000.
Vzducholoď
(Převzata z Codeforces, úloha 590B.)
Letíme vzducholodí a chceme se dostat z bodu A do bodu B (body jsou zadané souřadnicemi), ale situace je komplikovaná větrem. Otáčení vzducholodi netrvá žádný čas, ale vzducholoď má maximální rychlost v (oproti vzduchu). Prvních t sekund vane vítr s vektorem (wx, wy), po t sekundách se změní na vektor (ux, uy) a v tomto směru už zůstane.
Formálně, pokud má vzducholoď oproti větru nulovou rychlost a je na [x, y] a vane vítr (ux, uy), po τ sekundách bude vzducholoď na [x + τ·ux, y + τ·uy]. Maximální rychlost vzducholodi je vždy větší než velikost vektoru větru.
Za jak dlouho se nejrychleji dostaneme z A do B? (Maximální povolená odchylka je 10-6.)