Pátá série třicátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 37-5-1: Pekelná cesta
- 37-5-2: Fantomas se zlobí
- 37-5-3: Ledová socha
- 37-5-4: Užitečné mnohočleny
- 37-5-S: Vzestup zdrojového kódu
 37-5-1 Pekelná cesta (Zadání)
37-5-1 Pekelná cesta (Zadání)
Úloha od nás žiada nájsť zo všetkých ciest práve tú, ktorá je lexikograficky najmenšia.
Vôbec pritom nezáleží na dĺžke danej cesty.
Zadanie však pripomína, že na ceste sa žiadne vrcholy neopakujú.
To znamená, že v grafe existuje iba konečný počet ciest.
Ak zvládneme v lexikografickom poradí otestovať všetky,
tak prvá, ktorá bude obsahovať cieľový vrchol BOBER, je tá správna.
Otestovať všetky cesty v správnom poradí pritom dokážeme jednoduchou rekurziou vo vrcholoch grafu:
v každom vrchole skúsime cestu predĺžiť postupne o všetky vrcholy, do ktorých sa dá z neho dostať,
v ich lexikografickom poradí.
Začneme vrcholom ALICE.
Aby sme žiadny vrchol počas cesty nenavštívili viackrát, budeme si udržiavať množinu navštívených vrcholov (ktorá sa dá implementovať ako pole N bitov). To nám umožní v konštantnom čase zistiť, či už nejaký vrchol v ceste máme alebo nie. Pri rekurzívnom vnorení sa do nového vrcholu tento vrchol pridáme do množiny, pri návrate funkcie ho z nej odoberieme. Okrem toho si môžeme udržiavať aktuálnu cestu v poli, čo nám umožní ju na konci jednoducho vypísať. Pri vnorení sa do vrcholu ju vždy predĺžime o tento nový vrchol, pri návrate odoberieme posledný vrchol. Toto pole však nepotrebujeme, keď si uvedomíme, že zásobník volania rekurzívnych funkcií za nás už ukladá presne rovnaké informácie, cestu teda vieme zreprodukovať aj potom, ako ju nájdeme.
Taktýmto spôsobom vždy nájdeme správne riešenie, ale môže nám to trvať dosť dlho.
Predstavme si napríklad, že by s vrcholom ALICE susedili vrcholy
AAAAA, AAAAB, AAAAC ... ZZZZY,
ktoré by boli navzájom spojené do úplného grafu (každý s každým),
a potom vrchol ZZZZZ, ktorý by viedol do cieľového vrcholu.
Náš algoritmus by najskôr prehľadal všetkých (265 - 1)! permutácií (áno, je tam faktoriál!),
kým by sa vôbec pozrel na vrchol ZZZZZ.
Má exponenciálnu časovú zložitosť!
Zlepšiť to vieme jednoduchým pozorovaním:
predstavme si, že sme už v rámci predošlého prehľadávania navštívili vrchol W,
napríklad ABCDE,
prešli sme všetky možnosti, kam z neho pokračovať, a vrátili sme sa z neho.
V takom prípade si už môžeme vrchol W označiť ako nepriechodný –
tvrdíme, že ak sme sa doteraz nedostali do cieľového vrcholu (a prehľadávanie neskončili),
už sa nám to cez vrchol W nikdy nepodarí a môžeme ho ďalej preskakovať.
Dôkaz je, ehm, jemne zapeklitý. Tvrdenie je implikácia, dokážeme ju sporom. Negácia tvrdenia znie: doteraz sme sa nedostali do cieľového vrcholu a dokážeme sa tam dostať cestou cez W.
Pokiaľ sa do cieľa dokážeme dostať teraz, musí existovať aspoň jedna cesta z W do cieľového vrcholu. Zvoľme si lexikograficky najmenšiu z nich. Ak by sme po tejto ceste vedeli prejsť už predtým, vedeli by sme sa dostať do cieľa aj pri prvej návšteve W (a skončiť), čo je spor.
Zostáva možnosť, že sme po nej predtým prejsť nevedeli, musela teda obsahovať aspoň jeden vrchol, ktorý nám v tom zabránil – a to tým, že sme ho už navštívili na pôvodnej ceste do W a nemôžeme ho navštíviť znova. Označme si prvý vrchol cesty do W, ktorý nám takto bráni, ako V.
Z definície vyplýva, že existuje cesta zo štartu cez vrchol V do cieľového vrcholu, ktorá neobsahuje vrchol W – nájdeme ju tak, že zo sledu idúceho cez V, W a zase V „vystrihneme“ časť medzi dvomi návštevami V. V sme ale zvolili ako taký vrchol, ktorý na aktuálnej ceste do (opätovnej návštevy) W neleží, takže predtým, než sme sa dostali k opätovnej návšteve W, sme museli prehľadať všetky cesty vedúce z vrcholu V (a až potom sme mohli vrchol V opustiť). Museli sme preto nájsť aj cestu vedúcu z V do cieľa, čo je spor s tým, že sme sa nedostali do cieľa a teda doteraz neskončili prehľadávanie.
Tým sme dokázali, že opätovná návšteva W nemôže viesť k riešeniu, preto môžeme každý už prehľadaný vrchol ďalej ignorovať (všimnime si, že hoci je dôkaz zložitý, samotná myšlienka je veľmi intuitívna). Upravíme si teda našu rekurzívnu funkciu tak, aby pri návrate z každého vrcholu daný vrchol umiestnila do nejakej množiny nepriechodných vrcholov... alebo ešte jednoduchšie, nebudeme ho vôbec odoberať z množiny vrcholov navštívených (rýchlejší program teda získame odstránením riadku z programu pomalšieho – vskutku pekelné).
Tento prístup nám zabezpečí, že každý vrchol navštívime najviac raz a teda každú hranu skontrolujeme tiež najviac raz. Pred samotným prehľadávaním však musíme jednotlivé vrcholy lexikograficky utriediť. Preto je celková časová zložitosť O(M log M) (zadané máme iba hrany, vrcholov teda môže byť až O(M)). Pamäťová zložitosť je O(M).
 37-5-2 Fantomas se zlobí (Zadání)
37-5-2 Fantomas se zlobí (Zadání)
K této úloze šlo přistupovat mnoha způsoby, my si jeden konkrétní ukážeme. Můžeme si povšimnout, že vstup má velikost N2, tudíž libovolný algoritmus s časovou složitostí O(N2) je lineární s velikostí vstupu, tedy optimální.
Jako P[u][v] si označme v-té číslo na u-tém řádku vstupní matice, tedy číslo východu z místnosti u, kterým se z ní musíme vydat, abychom došli do místnosti v. Důležitá vlastnost úlohy je, že Fantomasovo doupě tvoří strom, a tedy mezi každými dvěma místnostmi existuje právě jedna cesta. V opačném případě by úloha neměla jednoznačné řešení.
Řešení funguje na jednoduché myšlence: co kdybychom pro libovolné dvě místnosti x a y uměli v konstantním čase rozhodnout, zda mezi nimi vede chodba? Pak už umíme vyřešit celou úlohu: stačí vyzkoušet všechny dvojice místností a ty, mezi kterými vede chodba, vypsat. Abychom dvojici nevypisovali dvakrát – jednou jako x, y a podruhé jako y, x – budeme iterovat jen přes dvojice, kde x < y. Těch je O(N2) a otestovat každou z nich nás dle našeho předpokladu stojí konstantní čas, tedy celková časová složitost algoritmu je O(N2).
Jak ale ze vstupu poznat, zda mezi x a y vede chodba? Pomůže nám následující tvrzení:
Nechť di[j] značí počet místností, do kterých se z i musíme vydat stejným východem, jako do j. Jinými slovy, di[j] je počet místností k takových, že P[i][k] = P[i][j]. Pak platí, že mezi x a y vede chodba právě tehdy, když dx[y] + dy[x] = N.
Tvrzení dokážeme následovně. Označme jako X množinu všech místností, do kterých se z x jde jiným východem, než tím do y; speciálně x ∈X. Pak platí, že dx[y] + |X| = N, jelikož do každé místnosti se buď jde stejným východem jako do y, nebo jiným. Úpravou dostáváme dx[y] = N - |X|. Obdobně zadefinujme Y jako množinu místností, do kterých se z y jde jiným východem, než tím do x. Opět platí, že dy[x] = N - |Y|.
Platí, že X a Y jsou disjunktní: kdyby existovala místnost v zároveň v X a Y, znamenalo by to, že můžeme vyrazit z x východem, který nevede k y a dojít do v (z definice X) a z něj přijít do y východem, který nevede k x (z definice Y) – to celé bez toho, abychom cestou znovu prošli x nebo y. To je nemožné, jelikož Fantomasovo doupě tvoří strom. X a Y jsou tedy disjunktní, a tedy platí |X| + |Y| ≤ N.
Zároveň si snadno rozmyslíme, že |X| + |Y| = N právě tehdy, když mezi x a y existuje chodba. V opačném případě totiž na cestě mezi x a y existuje aspoň jedna další místnost w. Ta není ani v X, ani v Y, a tedy |X| + |Y| ≤ N - 1 < N.
Nyní stačí poskládat nerovnosti dohromady. Máme dx[y] + dy[x] = N - |X| + N - |Y| = 2N - (|X| + |Y|) ≥ N, přičemž rovnost nastává právě tehdy, když x a y jsou spojeny chodbou, což je přesně to, co jsme chtěli dokázat.

Máme tedy jednoduchý způsob, jak poznat, že spolu dvě chodby sousedí: stačí otestovat, zda dx[y] + dy[x] = N. Zbývá si rozmyslet, jak toto dělat efektivně, tedy jak pro libovolné u a v spočítat du[v] v konstantním čase. Pro každou místnost u si vytvoříme pole A[u] velikosti odpovídající počtu východů z u, a pro i-tý východ si do A[u][i] uložíme počet místností v takových, že P[u][v] = i. Chceme-li pak znát hodnotu du[v], použijeme hodnotu A[u][P[u][v]].
Spočítání všech polí A[x] nám zabere čas O(n2) a jeden test, zda x a y jsou spojeny chodbou, zabere konstantní čas. Časová složitost celého algoritmu je tak O(n2).
Trhání listů
Uveďme ještě ve stručnosti jeden způsob, jak šla úloha řešit. Umíme poznat, zda je místnost list: vede z ní jen jediný východ. Budeme tedy listy postupně ze stromu odtrhávat. Konkrétně si pro každou místnost budeme udržovat počet aktivních východů a do kolika ještě nesmazaných místností který z nich vede.
Listy si udržujeme ve frontě, kterou ze začátku naplníme místnostmi s jediným aktivním východem. Když mažeme list u, tak aktualizujeme statistiky ve všech ostatních místnostech. Právě u jedné místnosti v se nám stane, že nám počet aktivních východů klesne o 1. Rozmyslete si, že to je místnost sousedící s u. Dvojici u, v vypíšeme. Pokud navíc místnosti v počet aktivních východů klesl na 1, přidáme ho do fronty listů. Tak pokračujeme, dokud je fronta neprázdná.
 37-5-3 Ledová socha (Zadání) (Komentáře)
37-5-3 Ledová socha (Zadání) (Komentáře)
Jak je u úloh, kde hledáme nejkratší/nejrychlejší cestu zvykem, řešení spočívá ve výrobě vhodného grafu. Kdyby socha nezrychlovala, bylo by řešení učebnicové: za každé volné políčko (políčko, kde není překážka) vyrobíme vrchol a každá dvě sousední volná políčka spojíme hranou. Na výsledný graf pustíme BFS a jsme hotovi. Máme-li R řádků a S sloupců, zvládneme konstrukci grafu i BFS v optimálním čase O(RS).
Socha ale umí zrychlovat. V každém okamžiku nás tudíž nezajímá jen její pozice, ale také její aktuální rychlost. Pojďme tedy vyrobit o něco složitější graf. Místo vrcholu pro každou možnou pozici sochy (tedy každé volné políčko) budeme mít vrchol pro každou dvojici (pozice, rychlost). Z jednoho vrcholu do druhého vede hrana, pokud se socha nacházející na jednom políčku s jednou rychlostí může v dalším kroku ocitnout na druhém políčku s druhou rychlostí, dle pravidel specifikovaných v zadání.
Zatím jsme graf popsali poněkud vágně a neřekli jsme, jak ho vyrobit, ale mělo by být zřejmé, že s ním bychom už měli vyhráno: stačí pustit BFS z vrcholu „start, nulová rychlost“ do vrcholu „cíl, nulová rychlost“. Z nalezené nejkratší cesty už snadno vyčteme, kdy máme kterým směrem sochu zrychlovat.
Ve zbytku řešení nám tedy zbývá odpovědět na dvě zásadní otázky: jak přesně tento graf vypadá? A jak ho efektivně vyrobit?
Začněme první otázkou. Vrchol budeme reprezentovat čtveřicí celých čísel: Čtveřice (p, q, r, s) označuje sochu na políčku (p, q) pohybující se rychlostí (r, s). To znamená, že – nezmění-li se její rychlost – bude v dalším kroku na políčku (p + r, q + s). Dle zadání je navíc r nebo s vždy nula. Zároveň určitě má smysl uvažovat jen rychlosti, kde -R ≤ r ≤ R a -S ≤ s ≤ S – jede-li socha ještě rychleji, pak v dalším kroku vyskočí z mapy, což není dovoleno. Celkově tedy pro každé z O(RS) políček máme O(R+S) různých rychlostí, tedy celkem má graf O(RS·(R+S)) vrcholů. Na konci řešení se ještě k počtu vrcholů vrátíme, ukáže se totiž, že nám jich stačí o dost méně.
Jaké máme v grafu hrany? Kromě speciálního případu vrcholů s nulovou rychlostí vedou z každého vrcholu nejvýše 3 hrany: do stavu, kdy rychlost zmenšíme o 1, ponecháme stejnou, nebo zvětšíme o 1. Každá taková hrana existuje ovšem jen tehdy, když daný vchol existuje (tedy např. nevylezeme z mapy) a nenachází-li se mezi původním a novým políčkem na mapě překážka.
Nyní už tedy víme, jak má graf vypadat na papíře. Pojďme ho efektivně sestrojit. K tomu nám stačí umět pro každou dvojici políček na stejném řádku nebo sloupci rychle testovat, zda mezi nimi existuje překážka. Žačněme s řádky, sloupce vyřešíme obdobně. Pořídíme si tabulku A, kde A[i][j] bude říkat vzdálenost k nejbližší překážce / konci mapy nalevo od políčka (i, j). Celé A spočteme jednoduchým průchodem zleva doprava. Když nyní máme dvě políčka, (r, s1) a (r, s2) pro s1 < s2, stačí se podívat, zda s2 - A[r][s2] < s1.
S tímto polem tedy umíme testovat existenci každé hrany v konstantním čase. Jelikož hran je nejvýše lineárně v počtu vrcholů, celková velikost grafu a časová složitost celého algoritmu je O(RS ·(R+S)).
Zrychlujeme, možná nevědomky
| k(k+1) |
| 2 |
Na závěr dodáme, že kdyby tato úloha byla praktická, dalo se takové složitosti dosáhnout i nevědomky: v praxi není potřeba nejdříve vytvářet celý graf a pak na něm pouštět BFS, stačí pustit BFS přímo na mapě a za běhu vytvářet ty vrcholy a hrany, na které se BFS právě ptá. A jelikož víme, že větší než odmocninové rychlosti nejsou potřeba, BFS do příslušných zbytečných vrcholů nikdy nedojde a náš algoritmus bude mít výše zmíněnou časovou složitost.
 37-5-4 Užitečné mnohočleny (Zadání)
37-5-4 Užitečné mnohočleny (Zadání)
Jak interpretovat násobení mnohočlenů
Než se vrhneme na samotná řešení jednotlivých podúloh, ukážeme si, že má násobení dvou mnohočlenů A(x) a B(x) velice pěknou a užitečnou geometrickou interpretaci.
Nejprve vezmeme seznam koeficientů mnohočlenu A(x) a jeho koeficienty zrcadlově otočíme. Následně vezmeme tento nový seznam a seznam koeficientů B(X), dáme je naproti sobě, a posuneme je tak, aby poslední koeficient otočeného A(x) ležel naproti nultému koeficientu B(x). Koeficienty píšeme v seznamech od nejmenšího směrem zleva doprava.
Poté začneme seznam A(x) posouvat doprava a při každém posunu (včetně počátečního) spočítáme skalární součin mezi překrývajícími se částmi obou seznamů. To znamená, že při každém posunu vynásobíme všechny dvojice koeficientů, které právě leží naproti sobě, a sečteme výsledky. Pokud má překryv nulovou délku, je výsledek součtu automaticky 0.
Jednotlivé součty, které takto získáme, budou odpovídat jednotlivým koeficientům výsledného součinu mnohočlenů A(x) a B(x). Konkrétně platí, že když jsme se posunuli oproti výchozí pozici o i pozic, získáme skalárním součinem hodnotu koeficientu i.
Pojďme dokázat, že je naše interpretace s posouváním seznamů správná. Uděláme to tak, že výsledek po i-tém posunu popíšeme pomocí vhodného součtu.
Nejprve doplníme oba seznamy koeficientů zprava nulami do nekonečna. Po zrcadlovém otočení seznamu koeficientů A(x) tedy tyto doplněné nuly povedou doleva. Tato úprava mohla způsobit, že se některé překryvy zvětšily, nicméně všechny nově vzniklé dvojice v překryvu obsahují nulový koeficient, takže nijak neovlivní výsledný součet.
Nyní můžeme výsledek po i-tém posunu snadno vyjádřit sumou. Představme si, že stojíme na pravém okraji překryvu. Tam bude vždy koeficient a0, který v tomto posunu leží naproti koeficientu bi.
Postupujeme od tohoto pravého okraje překryvu směrem doleva, až dojdeme na levý okraj překryvu, kde je koeficient b0. Cestou postupně sčítáme součiny naproti sobě ležících koeficientů. Díky doplnění se nikdy nestane, že by nějaký koeficient v překryvu nebyl v dvojici.
Koeficienty mnohočlenu B(x) se tedy postupně snižují, zatímco koeficienty otočeného A(x) se naopak zvyšují. Pro koeficient výsledku ci tak dostáváme následující součet:
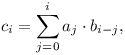
kde koeficienty mimo původní rozsah považujeme za nulové (vznikly doplněním).
Tato suma přesně odpovídá vyjádření i-tého koeficientu součinu mnohočlenů ze zadání, takže je náš důkaz hotový.
Rozmysleme si nakonec, že A(x) ·B(x) = B(x) ·A(x), takže lze násobení interpretovat i tak, že naopak otočíme zrcadlově seznam koeficientů B(x) a posouváme jej vůči seznamu A(x) směrem doprava.
Překryv jedniček
V možném naivním řešení této úlohy bychom vzali jeden z řetězců, posunuli jej tak, aby jeho konec ležel naproti začátku druhého řetězce, a začali jej postupně posouvat vůči druhému řetězci směrem doprava. Při každém posunu bychom spočítali všechny páry jedniček ležících v překryvu naproti sobě a po vyzkoušení všech posunů bychom vrátili maximum a odpovídající posun.
Všimněme si, že kontrolu toho, zda leží naproti sobě dvě jedničky, lze realizovat prostým násobením. Stačí vynásobit aktuálně zkoumané znaky jako čísla, kterým odpovídají, a získáme 1 právě tehdy, pokud jsou oba znaky jedničky. Pokud toto provedeme pro každou dvojici v překryvu a výsledky sečteme, získáme počet jedniček ležících při aktuálním posunu naproti sobě.
To se ovšem nápadně podobá naší interpretaci násobení mnohočlenů – v ní jsme posouvali jeden seznam vůči druhému, při každém posunu násobili naproti sobě ležící koeficienty a jejich součiny sčítali.
Zkusme tedy kalkulačce zadat takový vstup, aby nám pro každou vzájemnou pozici spočítala počet jedniček ležících naproti sobě. Nabízelo by se zadat kalkulačce rovnou řetězce převedené na seznamy čísel, nicméně musíme zohlednit, že v naší interpretaci je posouvaný seznam zrcadlově otočený.
Můžeme proto jeden ze seznamů zrcadlově otočit. Ten seznam, který otočíme, pak budeme považovat za ten, který v naší interpretaci posouváme vůči druhému.
Kalkulačka nám vrátí seznam koeficientů výsledného mnohočlenu, který udává počty jedniček ležících naproti sobě při jednotlivých posunech. Tento seznam může být kratší, než je celkový počet posunů. To se mohlo stát, pokud několik posledních posunů dávalo nulový výsledek, protože kalkulačka vrací výsledný seznam koeficientů od nultého po poslední nenulový. Takové nulové hodnoty si nicméně můžeme podle potřeby doplnit.
Nakonec stačí výsledný seznam projít a nalézt největší koeficient. Na základě toho, který ze seznamů jsme otočili a na jaké pozici ve výsledném seznamu se maximum nachází, pak snadno určíme, kterým řetězcem je třeba pohnout, jakým směrem a o kolik.
Násobili jsme seznamy s celkovou délkou O(N) a s konstantně velkými koeficienty, takže je časová složitost O(N log N).
Nejlepší shoda
Hledáme podřetězec délky jehly v seně, který má s jehlou co nejvíce shodných znaků.
Tento proces lze interpretovat následovně:
Zarovnáme jehlu a seno jejich začátky k sobě a postupně posouváme jehlu doprava. Pro každý posun spočítáme, kolik znaků na odpovídajících pozicích se shoduje. Nakonec vybereme posun s největším počtem shodných znaků.
Podobný problém jsme už řešili výše, kde jsme pomocí násobení mnohočlenů určovali, kolik jedniček leží naproti sobě pro všechny posuny. Rozmysleme si, že pokud v binárních řetězcích jedničky a nuly prohodíme, můžeme analogicky násobením určit, kolik nul leží naproti sobě.
Přesně to uděláme v našem řešení – nejprve určíme počet shodných jedniček pro každý posun (včetně přesahů jehly mimo seno) pomocí jednoho násobení mnohočlenů, a pak stejným způsobem určíme počet shodných nul. Tak jako minule jeden ze seznamů během obou násobení zrcadlově otočíme a koeficienty výsledku pak budou kódovat výsledky jeho jednotlivých posunů vůči druhému směrem zleva doprava. My si v tomto a ve zbylých řešeních pro přehlednost vždy zvolíme seznam jehly.
Nakonec projdeme všechny posuny, ve kterých jehla celá leží uvnitř sena, a vybereme ten, pro který je součet počtů shodných jedniček a shodných nul maximální.
Tento postup má opět časovou složitost O(N log N).
Představme si ještě alternativní řešení:
Znaky jehly i sena v něm zakódujeme tak, že všechny původní nuly nahradíme číslem -1 a jedničky ponecháme jako 1. Poté vynásobíme zrcadlově otočený seznam koeficientů jehly se seznamem koeficientů sena.
Všimněme si, že výsledný koeficient odpovídající určitému posunu nyní vyjadřuje rozdíl počtu shodných dvojic a počtu rozdílných dvojic v daném zarovnání. Protože zároveň víme, že součet počtů shodných a rozdílných dvojic znaků se rovná ve validních posunech délce jehly, dostáváme soustavu dvou rovnic, ze kterých lze snadno určit počet shodných znaků pro každý validní posun.
Výskyty s otazníky
Chceme najít všechny výskyty jehly v seně, přičemž jehla může obsahovat otazníky představující libovolné znaky. Posun označíme za výskyt tehdy, když každá jednička nebo nula v jehle leží naproti stejnému znaku v seně.
Podobně jako v předchozí úloze opět provedeme dvě násobení, která nám pro každý posun umožní určit, zda se jedná o platný výskyt. Nejdříve spočítáme, kolik jedniček z jehly leží pro každý posun naproti jedničkám v seně. Poté obdobně spočítáme, kolik nul z jehly leží pro každý posun naproti nulám v seně.
K spočítání stejných znaků konkrétního druhu ležících naproti sobě stačí vždy v obou řetězcích označit právě zkoumaný typ znaků jedničkou a všechny ostatní (včetně otazníků v jehle) nulou. Po provedení obou násobení pak v každém validním posunu zkontrolujeme, zda součet shodných jedniček a nul odpovídá počtu všech znaků jehly bez otazníků. V takovém případě je daný posun platným výskytem.
Celková složitost je O(N log N).
Ukažme si opět ve stručnosti alternativní řešení:
Nuly v obou řetězcích označíme číslem -1. Jedničky ponecháme označené jako 1. Otazníky v jehle označíme jako 0.
Po vynásobení otočeného seznamu jehly se seznamem sena bude každý výsledný koeficient odpovídat rozdílu mezi počtem shodných a neshodných dvojic znaků v daném posunu, přičemž bereme v úvahu pouze ty pozice, kde v jehle není otazník. Platí, že pokud je tento rozdíl roven počtu znaků jehly bez otazníků, nalezli jsme platný výskyt jehly v seně.
Regulární výrazy
Nabízí se podobný přístup, jako v prvním řešení předchozí úlohy, tedy nejprve zjistit pro každý znak (mimo otazník) a posun, kolik znaků daného druhu leží v dotyčném posunu naproti sobě, a vybrat takový posun, kde naproti sobě leží tolik znaků, jako je počet znaků jehly bez otazníků.
Takový přístup by měl pro abecedu Σ složitost O(|Σ| ·N log N), kde |Σ| značí velikost abecedy. To je rozumné řešení například pro text napsaný v české abecedě, nicméně příliš pomalé pro abecedu o velikosti O(N).
Místo toho si všimněme, že lze tento problém snadno převést na předchozí. Každý znak z abecedy Σ lze zakódovat pomocí ⌈ log |Σ|⌉ bitů. Nahradíme tedy každý znak obou řetězců jeho bitovým zápisem. Znak otazníku pak nahradíme posloupností ⌈ log |Σ|⌉ otazníků. Tím získáme řetězec délky O(N log |Σ|).
Na tento řetězec poté stačí aplikovat předchozí algoritmus. Pouze je třeba dát pozor, abychom při výběru správného posunu uvažovali jen validní posuny, tedy ty, které jsou násobkem ⌈ log |Σ|⌉.
Získali jsme tak řešení běžící v čase O(N log N log |Σ|).
Toto řešení je efektivní i pro abecedy o velikosti O(N) a stačilo na získání plného počtu bodů, nicméně si v následujícím oddílu ukážeme, že lze úlohu řešit stejně rychle jako v případě binární abecedy, tedy v O(N log N).
Regulární výrazy rychleji
Než začneme, převedeme jednotlivé znaky na různá nezáporná čísla. Znak otazníku převedeme na 0, zbylé znaky můžeme zakódovat libovolně, pouze s podmínkou, že přiřazená čísla budou mít velikost polynomiálně velkou vzhledem k součtu délek vstupních seznamů.
Nejprve si představíme naivní řešení této úlohy a následně jej zkusíme urychlit s pomocí Kevinovy kalkulačky.
Přímočarým řešením je postupně posouvat seznam jehly vůči senu směrem doprava. Při každém posunu, kdy jehla zcela leží uvnitř sena, stačí projít všechny dvojice znaků v překryvu a zkontrolovat, zda na sebe pasují.
Ukažme si nyní, jak tuto kontrolu překryvu formulovat numericky. Nechť L označuje délku jehly, jk označuje k-tý koeficient seznamu jehly a sk označuje k-tý koeficient sena. Definujeme ci, které bude vyjadřovat výsledek numerické kontroly překryvu při posunu o i pozic:
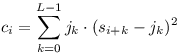
Rozmysleme si, že libovolný sčítanec sumy v tomto vzorci je roven nule právě tehdy, když je na pozici k v jehle otazník (tedy jk = 0), nebo znak v seně na pozici i+k odpovídá znaku v jehle (tedy si+k = jk).
Protože je každý sčítanec nezáporný, platí, že je celkový součet ci nulový právě tehdy, když všechny sčítance vyšly nulové, tedy když v daném posunu každý konkrétní znak jehly pasuje s odpovídajícím znakem sena.
Takto jsme převedli kontrolu platnosti překryvu na test, zda suma ci vyšla nulová. Pojďme si nyní rozmyslet, jak spočítat tuto sumu pro všechny posuny co nejrychleji.
Upravme nejprve náš vzorec pro kontrolu překryvu:
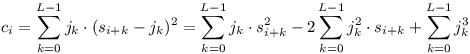
| L-1 |
| k=0 |
| 3 |
| k |
Zbylé dvě sumy už jsou zajímavější. Když si je nicméně podrobněji prohlédneme, zjistíme, že odpovídají nám dobře známé situaci. Obě sumy vezmou dva seznamy, jeden délky jehly, druhý délky sena, které jsou posunuté vůči sobě o i, vynásobí koeficienty ležící naproti sobě, a sečtou výsledky.
| L-1 |
| k=0 |
| 2 |
| i+k |
| L-1 |
| k=0 |
| 2 |
| k |
Tak získáme všechny potřebné hodnoty, s pomocí kterých poté snadno spočteme pro každý validní posun výsledek numerického porovnání a vybereme všechna taková, která vyšla nulová.
Protože provedeme jen dvě násobení, každé pracující s mnohočleny délky O(N), dosáhneme opravdu časové složitosti O(N log N).
Závěr
Dodejme na závěr, že lze mnohočleny s celočíselnými koeficienty skutečně násobit v čase O(N log N), takže všechna naše řešení mají opravdu uvedenou časovou složitost. Používá se k tomu algoritmus známý jako rychlá Fourierova transformace (zkráceně FFT).
Ten nachází překvapivě široká uplatnění – kromě násobení mnohočlenů a vyhledávání v textu se používá například při analýze a rozkladu zvukového signálu nebo při kompresi obrazových dat.
Dále jsou na něm založeny nejrychlejší známé algoritmy pro násobení celých čísel. V klasickém výpočetním modelu, ve kterém umíme pracovat s čísly polynomiálně velkými vzhledem k délce vstupu v konstantním čase, lze pomocí FFT dvě čísla o celkové délce N bitů vynásobit dokonce v čase O(N).
Pokud vás tento algoritmus zaujal, můžete si o jeho fungování a některých uplatněních přečíst v knize Průvodce labyrintem algoritmů.
 37-4-X1 Mehrdeutige Wortbildung (Zadání)
37-4-X1 Mehrdeutige Wortbildung (Zadání)
Řešení této úlohy najdete v řešení čtvrté série.
 37-5-S Vzestup zdrojového kódu (Zadání)
37-5-S Vzestup zdrojového kódu (Zadání)
Seriál lze odevzdávat za snížený počet bodů až do konce školního roku. Řešitelům, kteří už čtvrtou sérii odevzdali, rozešleme vzorové řešení napřímo. Pokud chceš tuto sérii přeskočit a začít řešit další díl, můžeš si o vzorové řešení napsat na ksp@mff.cuni.cz.