Pátá série třicátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám páté číslo hlavní kategorie 37. ročníku KSP.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.

Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.

Odměny & na Matfyz bez přijímaček

• Termín série: neděle 15. června 2025 ve 32:00 (tedy další ráno v 8:00)
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

• Odměna série: Odznáček do profilu na webu si vyslouží ten, kdo z každého dílu seriálu získá alespoň 2 body.

Zadání úloh

• 37-5-1: Pekelná cesta
• 37-5-2: Fantomas se zlobí
• 37-5-3: Ledová socha
• 37-5-4: Užitečné mnohočleny
• 37-5-S: Vzestup zdrojového kódu

37-5-1 Pekelná cesta (10 bodů)

Čertík Bertík má za úkol strašit spoustu domácností. Každá má svůj krb, mezi kterými se může pekelně přenášet. Kvůli šetření na meziprostorových cestách se ale z každého krbu může přenášet pouze mezi některými dvojicemi krbů – ne nutně mezi všemi. Aby si Bertík krby lépe zapamatoval, přiřadil každému z nich pětici velkých písmen z anglické abecedy. Tím se ale – jako správný čertík – moc chvástal na pekelných úřadech. Ty jsou proslulé svojí pekelností a nepochopitelností. Kvůli tomu mu teď zavedly novou pekelnou direktivu: musí mezi krby cestovat po lexikograficky nejmenších cestách. Bertík je z toho celý nesvůj, pomůžete mu?

Konkrétně, cesta mezi krby x a y je nějaká posloupnost na sebe navazujících krbů začínající na x a končící na y, kde se žádný krb neopakuje. Představíme-li si všechny možné cesty z x do y, pak ta lexikograficky nejmenší z nich je ta, která se, napíšeme-li za sebe názvy jejích krbů bez mezer, v řazení podle slovníku vyskytuje nejdříve.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na vstupu dostanete neorientovaný graf krbové sítě pomocí hran. Na prvním řádku je počet hran M, na každém dalším dvě pětice velkých písmen oddělených spojovníkem – hrana vede mezi dvěma těmito krby.

Formát výstupu: Vypište, jak se má Bertík dostat z krbu ALICE do BOBER. To zahrnuje i tyto krby. Mezi krby pište ->.

8
ALICE-BOBER
ALICE-ALLAN
ALICE-ALBUS
ALBUS-EIDAM
ALBUS-ALLAN
EIDAM-BOBER
ALBUS-BOBER
ALLAN-BOBER

ALICE->ALBUS->ALLAN->BOBER

Vysvětlení ukázkového vstupu: Bertík by se sice mohl z krbu ALICE rovnou přesunout do krbu BOBER, to by ale jeho cesta nebyla lexikograficky nejmenší, jelikož ALICEA… je ve slovníkovém řazení před ALICEB… Z podobného důvodu Bertík nemůže použít cestu ALICE->ALLAN->BOBER.

37-5-2 Fantomas se zlobí (11 bodů)

Tajným službám se konečně podařilo objevit Fantomasovo doupě – systém tunelů a chodeb kdesi ve francouzských Alpách. Než se do nich ale vydají Fantomase dopadnout a konečně ho dohnat ke spravedlnosti, chtějí si jeskyně pořádně zmapovat.

Fantomasovo doupě se skládá z N místností propojených N-1 chodbami, přičemž z každé místnosti se dá dojít do každé jiné. Informatik by řekl, že doupě je (neorientovaný) strom.

Naštěstí pro tajné služby má Fantomas mnoho poskoků a ne všichni se ve spletité síti chodeb orientují. Proto Fantomas nechal do každé místnosti umístit rozcestník. Rozcestník je nadepsaný názvem aktuální místnosti a pro každou z N-1 ostatních místností je na něm napsáno, kterou chodbou vycházející z aktuální místnosti se máme vydat, abychom došli do dané místnosti.

Tajným službám se podařilo získat všech N rozcestníků. Pomůžete jim zrekonstruovat mapu Fantomasova doupěte?

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku je číslo N – počet místností. Následuje N řádků. Na i-tém z nich je popis i-té místnosti zadaný seznamem N čísel. Konkrétně j-té číslo říká, jakým východem se vydat do místnosti j. (Pokud i = j, pak je odpovídající číslo 0.) Východy z každé místnosti mají v nějakém pořadí přiřazena čísla 1, … , d kde d je počet chodeb vedoucích z této místnosti.

Formát výstupu: Vypište N - 1 řádků popisujících chodby Fantomasova doupěte. Konkrétně, pro každou chodbu vypište na na vlastní řádek čísla dvou místností, které spojuje, oddělená mezerou. Chodby můžete vypsat v libovolném pořadí. Místnosti číslujeme od jedné.

10
0 1 1 1 1 1 1 1 1 1
1 0 2 2 2 2 2 2 2 2
2 2 0 2 2 2 2 3 3 1
1 1 2 0 2 2 1 2 2 2
1 1 3 1 0 2 1 3 3 3
1 1 1 1 1 0 1 1 1 1
1 1 2 2 2 2 0 2 2 2
1 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 1 2 0 1
1 1 1 1 1 1 1 1 1 0

1 2
3 5
4 5
5 6
2 7
4 7
3 9
8 9
3 10

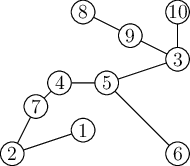
Podíváme-li se na místnost 5 ve vyobrazeném ukázkovém vstupu, můžeme si všimnout, že východ směrem k místnosti 4 dostal číslo 1, východ směrem k místnosti 6 číslo 2, a východ směrem k místnosti 3 dostal číslo 3. Abychom se dostali z místnosti 5 například do místnosti 10, musíme použít východ 3, proto je v pátém řádku na desáté pozici číslo 3.

37-5-3 Ledová socha (12 bodů)

V království hrochů je dnes obrovská slavnost. Celá země se sešla v rozpáleném paláci uprostřed savany, aby zde oslavila sňatek královy dcery Hrochtenzie s princem Robeartem z Království ledních medvědů na dalekém severu. Svatba je vrcholem desetiletí úsilí diplomatů z obou království – všichni očekávají, že spojí dva znepřátelené národy do jednoho impéria táhnoucího se od rovníku až k pólu, a jednou provždy ukončí zbytečné války a podezíravost, která mezi obyvateli království po staletí panovala.

A ještě víc než kdy jindy teď záleží na detailech – každá zpackaná drobnost by mohla být chybně interpretována jako urážka a způsobit okamžité rozbroje přímo na místě. A to už nikdo nechce zažít. Opravdu.

Jak to ale bývá, chybičky se občas vloudí, a tak se dodávka nadživotní ledové sochy zachycující ve všech detailech nadpozemskou krásu hroší princezny – mimochodem, z hlediska výroby mimořádně nákladného svatebního daru – opozdila. Dokonce až tak moc, že všechny stoly a židle (s netrpělivě čekajícími hrochy a ledními medvědy) jsou již rozestavěny na mřížce paláce a náklaďák se sochou se přes ně nemůže dostat k podstavci, kde by socha měla stát.

A to je větší problém, než se zdá. Podstavec je speciálně chlazený a stíněný tak, aby na něm socha vydržela v původním stavu. Jenže od momentu, kdy ji vyloží z bezpečí náklaďáku, budou všechny její detaily vydány napospas spalujícímu polednímu slunci. Sochu je tedy nutné dostat na podstavec co nejdříve.

A to nebude snadné. Za prvé, socha je, jak jste si patrně všimli, z ledu. Takže klouže. Hodně. A taky je opravdu těžká (tady se poznámky, z úcty k princezně, zdržíme). S vypětím všech sil je ji možné roztlačit na určitou rychlost. Pak si všichni zainteresovaní musejí na nějaký čas oddechnout, zatímco socha veselo klouže dál konstantní rychlostí. Pak je možné sochu znovu více zrychlit, nebo zpomalit, ale opět jenom o stejnou hodnotu rychlosti (aplikací stejné síly).

Konkrétně to vypadá tak, že v každém kroku je možné sochu zrychlit nebo zpomalit o hodnotu rychlosti jedno pole za krok v horizontálním nebo vertikálním směru (nebo v daném kroku rychlost neměnit). Socha se pak posune o tolik polí, jaká je její aktuální rychlost. Pak následuje další krok. Jelikož je socha velice křehká, nesmí se stát, že by po cestě narazila do jakékoliv překážky. Pro změnu směru pohybu je nutno sochu nejdříve zastavit (jinak by hrozilo, že se začne nekontrolovatelně točit, a to nemůže dopadnout dobře) – tedy pokud se socha pohybuje směrem nahoru rychlostí 3, ale chceme ji posunout směrem doleva, musíme jí nejdříve ťrikrát spomalit (příčemž se stihne poklouznout nejdřív o dvě a pak ješte o jedno pole) a až poté jí můžeme potlačit doleva.

Všechny zraky se upírají na vás. Máte k dispozici plánek paláce (rozdělený na volná políčka a políčka s překážkami), aktuální souřadnice sochy a souřadnice podstavce, kde musí socha skončit (s nulovou rychlostí, samozřejmě). Odpovězte takovou sekvencí zrychlení a zpomalení, která jí tam dostane v co nejmenším počtu kroků.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

37-5-4 Užitečné mnohočleny (12 bodů)

Kevin si letos koledováním přišel na rekordní množství vajíček, která následně výhodně prodal. Za utržené peníze si pořídil novou kalkulačku – ten nejdražší a nejmodernější model se spoustou různých funkcí.

Kevina z nich nejvíce zaujala funkce rychlého násobení mnohočlenů s celočíselnými koeficienty.

Připomeňme, že násobení mnohočlenů je definováno následovně:

Máme-li dva mnohočleny:

pak jejich součin:

je opět mnohočlen, jehož koeficienty c_i jsou dány vztahem:

kde chápeme a_j = 0 pro j > m a b_i-j = 0 pro i-j > k.

Kevina při čtení návodu překvapilo, že umí kalkulačka nalézt součin rychleji, než to umí klasický školní algoritmus.

Napadlo jej proto, že by mohlo jít kalkulačku využít k řešení několika problémů, nad kterými si již dlouho láme hlavu.

To bude vaším úkolem. Na konci zadání naleznete čtyři různé problémy a budete mít za úkol k nim najít efektivní řešení.

K tomu můžete využít Kevinovu kalkulačku. Tu má váš algoritmus k dispozici jako funkci, která na vstupu přijímá dva mnohočleny s celočíselnými koeficienty reprezentované jako seznamy jejich koeficientů (od nultého koeficientu po poslední nenulový), a vrací jejich součin ve stejné reprezentaci. Tuto funkci můžete ve vašem algoritmu zavolat libovolněkrát.

Při určování výsledné časové složitosti můžete předpokládat, že má tato funkce časovou složitost O(N log N), kde N je součet délek obou vstupních seznamů koeficientů. Koeficienty v seznamech zadaných kalkulačce by měly být polynomiálně velké k velikosti vstupu celého algoritmu.

Nyní již k samotným problémům. Ty jsou následující:

Úkol 1 – Překryv jedniček [2b]

Máme dva binární textové řetězce (složené z nul a jedniček) s celkovou délkou N. Na počátku leží tyto řetězce naproti sobě a jejich začátky jsou zarovnány. Cílem je jeden z řetězců posunout o libovolný počet znaků doleva či doprava vůči druhému tak, aby naproti sobě leželo co nejvíce jedniček. Znaky, které po posunu neleží naproti jinému znaku, ignorujeme.

Například v případě řetězců 10110 a 001010 je optimální posun takový, že třetí znak druhého řetězce leží naproti prvnímu znaku prvního řetězce. V tomto uspořádání jsou naproti sobě dva páry jedniček.

Úkol 2 – Nejlepší shoda [3b]

Jsou dány dva binární textové řetězce s celkovou délkou N, jeden delší (označme jej seno) a jeden kratší (jehla). Najděte takový podřetězec sena délky rovné jehle, který má s jehlou nejvíce shodných znaků na odpovídajících pozicích.

Například pro seno 00100100 a jehlu 1011 je nejlepší shoda s podřetězcem začínajícím na 3. pozici, který se od jehly liší v jediném znaku.

Úkol 3 – Výskyt s otazníky [3b]

Opět máme seno a jehlu s celkovou délkou N, přičemž seno je binární řetězec. Jehla však kromě nul a jedniček může obsahovat i otazníky, které reprezentují libovolný znak - nulu i jedničku. Různé otazníky mohou být nahrazeny různými znaky. Vaším úkolem je najít všechny výskyty jehly v seně.

Například pro seno 110011110 a jehlu ?11?1 se jehla v seně vyskytuje pouze jednou, a to od 4. pozice.

Úkol 4 – Regulární výrazy [4b]

Tentokrát řešíme obdobný problém, jako v předchozím úkolu, ale seno i jehla jsou tvořeny znaky z obecné abecedy, nikoliv jen z nul a jedniček. Jehla může opět obsahovat otazníky, které zastupují libovolný znak této abecedy.

Mějme například seno abcbbcbc a jehlu ?bc. Správným řešením je vypsat pozice 1, 4 a 6. Všimněte si, že se výskyty částečně překrývají.

Váš algoritmus by měl být na plný počet bodů efektivní i v případě, že má abeceda velikost O(N).

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

37-4-X1 Mehrdeutige Wortbildung (10 bodů)

Protože se nikomu nepodařilo X-kovou úlohu z čtvrté série vyřešit, rozhodli jsme se, že prodloužíme její deadline do konce páté série. Navíc vydáváme následující nápovědu, která vám snad pomůže k řešení.

U této úlohy vám pomůže známá nápověda: Sestrojte si vhodný graf. Na řetězce se pak můžete dívat jako na procházky v tomto grafu.

37-5-S Vzestup zdrojového kódu (15 bodů)

Pátý díl seriálu se ještě připravuje. Nezoufejte, bude již brzy!