První série třicátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 37-1-1: Tramvajová zástavka
- 37-1-2: Povodeň
- 37-1-3: Zpřeházená fronta
- 37-1-4: Nuly a jedničky
- 37-1-S: Návrat virtuálního stroje
- 37-1-X1: Bomberman
 37-1-1 Tramvajová zástavka (Zadání)
37-1-1 Tramvajová zástavka (Zadání)
Na vstupu jsme dostali rozpis n tramvajových odjezdů, seřazených vzestupně podle času. V tomto rozpisu budeme pracovat s „posuvným okénkem“, představujícím nějaký časový interval, a budeme si udržovat, kolik různých linek během tohoto intervalu odjíždí. Nakonec vypíšeme nejkratší interval, během kterého odjíždí všech k linek.

Přesněji řečeno, na začátku okénko bude obsahovat jen první tramvaj dne. Dále budeme opakovat následující:
- odjíždí-li během aktuálního okénka všechny linky, a toto okénko je zatím nejkratší takové, zapíšeme si ho. Potom posuneme levým okrajem okénka o jednu tramvaj dál.
- Neodjíždí-li během něj všechny linky, posuneme pravý okraj okénka o jednu tramvaj dál.
Můžeme promyslet, že tento jednoduchý algoritmus opravdu nalezne nejkratší časový úsek. Na konci nejkratšího možného úseku nutně odjíždí linka, která během úseku dříve nejede (jinak se úsek dal zprava zkrátit a není nejkratší). Proto v momentu, kdy se pravý okraj našeho okénka při běhu algoritmu dostal na konec tohoto úseku, byl náš levý okraj nanejvýš v levém okraji úseku, ale ne dál (levý okraj posouváme jen tehdy, když okénko obsahuje odjezdy všech linek). Díky tomu taky algoritmus dojde do bodu, kdy okénko obsahuje přesně nejkratší časový úsek, jen tam musí dojít levý okraj.
Algoritmus potřebuje pouze lineární čas O(n), protože ukazatel na levý okraj okénka, který si udržujeme, se zvýší maximálně 2n-krát, a stejně tak pravý okraj. V každé iteraci přitom uděláme jen konstantní množství operací.
Abychom každou iteraci stihli v konstantním čase, musíme ještě správně udržovat informaci o tom, zda v aktuálním okénku odjíždí všechny linky. Pojďme tedy v proměnné p udržovat počet různých linek, které během okénka odjíždí. Pokud jsou linky číslované od 1 do k, nabízí se použít k-prvkové pole, ve kterém i-té číslo představuje počet tramvají s číslem i, které během uvažovaného intervalu odjíždí. Tak při posunutí libovolného ukazatele můžeme toto číslo zvýšit, nebo snížit, a pokud tím klesne na 0, resp. stoupne z nuly na 1, upravíme i proměnnou p. Tím skutečně dostaneme konstantní čas.
Generátor vstupů úlohy opravdu generuje čísla tramvají od 1 do k, ale zadání to technicky neslibuje. Pokud na to nechceme spoléhat, dá se místo pole použít slovník (hešovací tabulka). Ten pracuje v konstantním čase v průměru (v tom smyslu, že našich m operací s prvky slovníku zabere ve střední hodnotě méně než cm operací procesoru pro nějakou konstantu c, a navíc je velmi nízká pravděpodobnost, že toto omezení překročí). Nejde však o konstantní čas v nejhorším případě. Touto cestou se vydal náš vzorový program. Další variantou, která nespoléhá na pravděpodobnost, je například místo hešovací tabulky použít binární vyhledávací strom. Ten ale bude udržovat až k různých hodnot, a místo konstantního času tak dostaneme čas O(log k) na operaci.
 37-1-2 Povodeň (Zadání)
37-1-2 Povodeň (Zadání)
Nejprve se podrobně podívejme na mechaniku barikád. To, zda políčko můžeme zabarikádovat, záleží pouze na tom, jestli se kolem něj nacházejí stěny. Barikády tedy můžeme pokládat nezávisle na sobě. To speciálně znamená, že každé rozmístění barikád lze doplnit na rozmístění, které má zabarikádované všechna možná políčka (tomuto rozmístění budeme říkat maximální).
Nyní si představme, že už jsme našli optimální řešení (tedy takové, ve kterém zatopíme co nejméně polí, a sekundárně použijeme co nejméně barikád). Co o něm ještě zvládneme říct?
Nahlédneme, že počet zatopených polí v optimálním řešení bude aspoň tak velký jako v řešení maximálním. To plyne z obecného pozorování, že přidáním barikády do libovolného rozmístění počet zatopených políček nestoupne. Tím pádem libovolné rozmístění musí vždy zatopit aspoň tolik polí jako maximální řešení, neboť po doplnění všech barikád do tohoto rozmístění může počet zatopených polí pouze klesnout nebo zůstat stejný.
Také si všimneme, že optimální řešení zatopí nejvýše tolik polí jako maximální. Kdyby tomu tak nebylo, tedy v maximálním řešení bychom zatopili méně políček než v maximálním, naše řešení by nemohlo být optimální.
Suma sumárum optimální rozmístění zatopí stejně políček jako rozmístění maximální. Tato informace se nám při hledání optimálního řešení bude velmi hodit, neboť maximální řešení umíme přímočaře zkonstruovat.
V neposlední řadě ukážeme, že v optimálním řešení se nachází všechny bariéry, které sousedí s aspoň jedním zatopeným polem v maximálním řešení. Již víme, že každé rozmístění lze vyrobit z toho maximálního odebráním některých barikád. Po odebrání barikády se počet zatopených políček buď nezmění, nebo stoupne. Pokud stoupne, dojde k tomu právě tehdy, když daná barikáda stála na hranici s vodou.
Tím pádem libovolné rozmístění, které nemá stejnou hranici s vodou jako maximální řešení, zatopí víc políček, než je optimum. Z toho plyne, že optimální řešení musí mít stejné barikády na hranici s vodou jako řešení maximální.
To celé nám dává jednoduchý návod, jak z maximálního řešení zkonstruovat řešení optimální. Jelikož víme, že obě řešení mají tu samou hranici s vodou, stačí z maximálního řešení odebrat všechny barikády, které na hranici neleží. Z předchozích úvah tak zaručeně dostáváme rozmístění, které Smolinec zatopí co nejméně, a spotřebuje přitom co nejméně barikád.
Hledání optima pak můžeme naprogramovat např. pomocí tří průchodů vstupní mřížkou. V prvním průchodu položíme barikády na všechna políčka, kam umístit jdou (vytvoříme maximální rozmístění). Ve druhém průchodu simulujeme velkou potopu, což jde například pomocí algoritmu prohledávání do šířky. V posledním průchodu najdeme barikády, které leží na hranici s vodou, nahlásíme je a máme hotovo.
Jelikož nad mřížkou velikosti R×S provádíme konstantně mnoho lineárních průchodů, časová i paměťová složitost řešení činí O(RS). Rychleji to zřejmě nepůjde, neboť samotné načtení a uložení vstupu rovněž zabere O(RS) času i paměti. Prozradíme ale, že řešení lze nalézt v jediném průchodu načteným vstupním polem (zkuste si to! ;-).
 37-1-3 Zpřeházená fronta (Zadání)
37-1-3 Zpřeházená fronta (Zadání)
Zadání úlohy si můžeme představit jako orientovaný graf. Jednotlivé pozice ve frontě si představíme jako vrcholy a hrana z vrcholu u do vrcholu v pak říká, že z místa vrcholu u se má nějaký student přesunout na místo vrcholu v. Všimneme si, že z každého vrcholu právě jedna hrana vychází a do každého vrcholu také právě jedna přichází.
Na vstupu máme graf zadaný tak, že v každém vrcholu máme napsané, kam z něj vedou hrany. Na výstup pak chceme mít v každém vrcholu zapsáno, odkud tam vede hrana. To si také můžeme představit tak, že chceme otočit směr všech hran a zůstat u původního formátu.
Jelikož mají všechny vrcholy právě jednu vstupní a výstupní hranu, tak jednotlivé komponenty grafu jsou orientované cykly. Ty mohou být i degenerované – např. jen s jedním vrcholem s hranou do sebe (student už je na správném místě) nebo s dvěma vrcholy reprezentující dvojici studentů, co se mají prohodit.

Každou komponentu zvládneme jednoduše otočit. Začneme v nějakém vrcholu a projdeme cyklus dokola a průběžně budeme otáčet hrany, kterými projdeme. To můžeme implementovat tak, že předposlednímu navštívenému vrcholu nastavíme následující vrchol na předpředposlední navštívený (pokud oba už existují, jinak nic neděláme). Toto budeme opakovat až do doby, než se vrátíme do vrcholu, kde jsme začali. Takto otočíme všechny hrany až na poslední, ale tu snadno zpravíme. Rozmyslete si, ze tento postup funguje i na degenerované cykly.
Cyklus tímto algoritmem umíme otočit v čase lineárním vzhledem k jeho délce. Stačí si pamatovat jen vrchol, kde jsme začali, aktuální a dva předcházející vrcholy.
Nyní by se nám hodilo použít tento algoritmus na všechny cykly v grafu. V tom je ale drobná komplikace. Kdybychom postupně procházeli vrcholy a u každého otočili cyklus, na kterém je, tak bychom některé cykly otočili vícekrát a finálně by skončili v původní orientaci. Kdybychom měli k dispozici více paměti, tak bychom si u každého vrcholu mohli pamatovat, jestli jeho cyklus byl už zpracován. Takto bychom získali algoritmus s časem v O(N), nicméně díky omezenému množství paměti ho nemůžeme použít.
Potřebujeme tedy bez přidané paměti u každého cyklu zařídit aby počet jeho otočení byl lichý – v našem případě to bude vždy právě jednou. Využijeme toho, že máme vrcholy očíslované jejich pozicí ve frontě. Na každém cyklu je právě jeden vrchol nejmenší hodnotou. Pro každý vrchol tedy ověříme, jestli se jedná o vrchol nejmenší hodnotu a pokud ano, tak ho otočíme. V průběhu algoritmu tedy budeme mít nějaké cykly již otočené a nějaké ne, ale to na nejmenší hodnotu cyklů nemá vliv. Dle našeho algoritmu však každý cyklus otočíme hned, jak na něj poprvé narazíme. Zjištění, jestli je vrchol nejmenší, budeme dělat tak, že vždy celý cyklus projdeme a zjistíme, jestli je tam nějaký menší.
Celková časová složitost je O(N2) – z každého vrcholu procházíme dvakrát cyklus o až N vrcholech. S trochou preciznosti se dá rozmyslet, že potřebujeme jen čtyři proměnné obsahující čísla vrcholů.
 37-1-4 Nuly a jedničky (Zadání)
37-1-4 Nuly a jedničky (Zadání)
A jak dlouhý bude výstup?
Protože není vůbec jasné, jak výstup bude dlouhý, ukažme horní odhad. Konstruujme čísla ze samých jedniček:
Rozdělme a1 až aN+1 do přihrádek podle zbytku po dělení N. Protože existuje pouze N zbytků, v alespoň jedné přihrádce budou alespoň dvě čísla, označme je ai, aj. Potom |ai - aj| je složené z jedniček a nul a má hledaný zbytek. (Nicméně požadované číslo může být menší.) Toto nám alespoň dává odhad, že výstup nebude delší než O(N).
Dynamika
Použijme dynamické programování. Označme si dp[ℓ][z][j] to, jestli zvládneme vyrobit číslo délky ℓ se zbytkem z po dělení N. Navíc si udržujme j – jestli jsme použili alespoň jednu jedničku:
Všechny ostatní nastavme zatím na lež.
Vyrábět nová zvládneme přidáním nuly nebo jedničky na začátek. Mohou ale obsahovat nuly na začátku, takže jim říkejme čísla*. Pokud má číslo* délku ℓ a přidáme na začátek nulu, tak jeho zbytek po dělení se nezmění:
Přidáním jedničky na začátek čísla* k jeho hodnotě přičteme 10ℓ:
(Čísla 10i si můžeme předpočítat až do 10n.)
Skončíme, když dojdeme k dp[ℓ][0][pravda]. Toto číslo* má alespoň jednu jedničku, zároveň tato jednička bude na začátku, jinak bychom vzali menší ℓ před přidáním nuly. Je to tedy číslo.
Nicméně nyní víme jen správnou délku. Nejmenší možné číslo zkonstruujeme zpětně pomocí zpětných ukazatelů. Pokud to jde, vždy budeme skákat zpět po přidání nuly. (Všimněme si, že do dp[ℓ][z][j] se dá dostat pouze ze dvou čísel*.)
A jaká je naše výsledná časová složitost? Pro stav děláme konstantní počet operací – přidáváme jedničku a nulu. Stavů máme nejvýše (N+1)×N×2, tedy O(N2). Celková časová složitost bude tedy O(N2). Na zpětné ukazatele si pamatujeme všechny stavy, tedy použijeme celkem O(N2) paměti.
Představme si graf
Na to abychom naše řešení zrychlili, si představme úplně jiný graf, než by nám nabízelo dynamické programování. Vrcholy budou tvořit zbytky 0 až N-1 a hrany budou odpovídat přidání jedničky nebo nuly doprava. Pokud máme zbytek z, přidání nuly na konec nám vytvoří zbytek 10z mod N, jedničky (10z+1) mod N.
Například pro N=6 by graf vypadal následovně (šedé hrany odpovídají přidání nuly a černé přidání jedničky, smyčky nejsou vyznačeny):

Na začátku máme k dispozici číslo 1 a budeme přidávat číslice doprava. Chceme skončit se zbytkem 0. Čísla dělitelná N tedy odpovídají sledům z 1 do 0 v tomto grafu.
Nyní tedy chceme najít nejmenší číslo. Hledaný sled tedy bude nejkratší a zároveň bude od předních pozic preferovat nuly před jedničkami. A nejkratší sled je cesta (stačí škrtnou část mezi prvním opakujícím se vrcholem), tedy pojďme najít nejkratší cestu – použijme BFS.
A jak vyřešíme preferování nul? Stačí v každém vrcholu nejdříve přidat do fronty hranu s nulou a teprve potom hranu s jedničkou. Podívejme se jaké bude pořadí všech cest délky i ve frontě. Cestu délky 0 máme jednu, a poté vždy ke každé přidáme doprava nulu a pak jedničku:
Tedy BFS přidá do fronty hledaná cesty v pořadí od nejmenší. Proto první nalezená cesta do nuly bude odpovídat nejmenšímu číslu.
Pro samotnou konstrukci čísla stačí jít po zpětných ukazatelích v BFS a na začátek čísla přidat 1.
Protože pouštíme BFS na graf s N vrcholy a N hranami, časová i paměťová složitost bude O(N).
 37-1-X1 Bomberman (Zadání)
37-1-X1 Bomberman (Zadání)
Představme si mřížku s vyznačenými políčky, která máme zničit:

Stačí nám položit čtyři bomby, aby zničily řádky 1 a 3 a sloupce A a D.
Od mřížky ke grafu
Situaci můžeme ekvivalentně popsat bipartitním grafem:
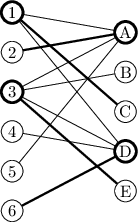
Vrcholy v levé partitě budou odpovídat řádkům, v pravé sloupcům. Hranu mezi řádek a sloupec natáhneme, kdykoliv v jejich průsečíku leží poličko ke zničení. Chceme tedy označit co nejméně vrcholů tak, abychom každé hraně označili aspoň jeden konec. Tomu se říká nejmenší vrcholové pokrytí grafu a pro obecné grafy je NP-těžké ho najít. Pro bipartitní grafy je ovšem spousta NP-těžkých problémů polynomiální … a často je můžeme řešit převodem na toky v sítích.
Od pokrytí k párování
Jeden takový známý problém je největší párování – chceme vybrat co největší množinu hran tak, aby žádné dvě neměly společný vrchol. Na našem obrázku je jedno z největších párování vyznačeno tučně.
Jak souvisí párování s pokrytími? Jelikož jeden vrchol může pokrýt nejvýše jednu hranu párování, musí mít každé vrcholové pokrytí aspoň tolik vrcholů, kolik hran má největší párování. Pro bipartitní grafy dokonce platí rovnost – tomu se říká Königova věta, ale její tvrzení nám neříká, jak pokrytí z párování vyrobit.
Od párování k tokům
Když už jsme narazili na párování, vzpomeneme si na standardní převod párování na toky, který nejdeme například v kuchařce o tocích nebo v Průvodci labyrintem algoritmů.
Vyrobíme následující síť:
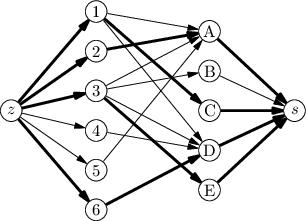
K bipartitnímu grafu přidáme „úplně doleva“ zdroj z a „úplně doprava“ spotřebič s. Původním vrcholům budeme říkat vnitřní, zdroji a spotřebiči vnější. K původním vnitřním hranám přidáme vnější: zdroj spojíme vnějšími hranami se všemi vrcholy levé partity, spotřebič se všemi vrcholy pravé partity. Všechny hrany zorientujeme zleva doprava a nastavíme jim kapacitu 1. Najdeme maximální celočíselný tok, například Fordovým-Fulkersonovým algoritmem, který má pro jednotkové kapacity složitost O(nm), kde n je počet vrcholů a m počet hran sítě.
Teď si všimneme, že vnitřní hrany, po kterých něco teče, tvoří párování: kdyby se nějaké dvě potkaly napravo, bude do nějakého vrcholu pravé partity přitékat aspoň 2, ale odtéci může maximálně 1. Podobně kdyby se hrany potkaly nalevo. Vyrobili jsme tedy z toku velikosti t párování o t hranách. Naopak z párování můžeme vyrobit tok stejné velikosti: kdykoliv je uv hrana párování, necháme téci 1 po hranách zu, uv, vs. Sestrojili jsme tedy bijekci mezi toky a párováními, která zachovává velikost, takže největší tok odpovídá největšímu párování. V čase O(nm) tedy umíme najít největší párování.
Od toků k řezům
Z teorie toků víme, že maximální tok odpovídá minimálnímu řezu. A zatímco toky v naší síti odpovídají párováním, řezy odpovídají vrcholovým pokrytím.
Bude se nám hodit trochu obecnější pohled na řezy: zs-řez (budeme říkat krátce řez) je množina hran taková, že každá (orientovaná) cesta ze z do s obsahuje aspoň jednu hranu řezu. Tedy pokud z grafu odstraníme všechny hrany řezu, přeřízneme všechny cesty ze z do s.
Ukážeme, jak z jakéhokoliv minimálního řezu vyrobit minimální vrcholové pokrytí. Nejprve řez upravíme do speciálního tvaru, budeme mu říkat třeba okrajový řez. To je řez, který používá jen krajní hrany (ty vedoucí ze zdroje nebo do spotřebiče). Kdyby minimální řez nebyl okrajový, můžeme každou vnitřní hranu uv nahradit hranou zu nebo vs. Tím ho nezvětšíme, a přitom bude stále řezat všechny cesty. (Alternativně bychom mohli vnitřním hranám nastavit kapacitu +∞, takže by ne-okrajové řezy nemohly být minimální. Ale pak bychom museli znovu analyzovat složitost F-F algoritmu.)
Teď už stačí pro každou vnější hranu řezu vybrat její vnitřní vrchol a vznikne vrcholové pokrytí. Vskutku: kdyby existovala nepokrytá hrana uv, cesta zuvs by nebyla přeříznuta. A naopak: z každého vrcholového pokrytí umíme vyrobit stejně velký okrajový řez – stačí uvážit hrany mezi z resp. s a vrcholy pokrytí.
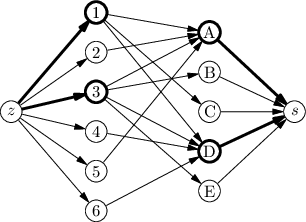
Máme tedy bijekci mezi okrajovými řezy a vrcholovými pokrytími, která zachovává velikost. Takže minimální okrajový řez odpovídá minimálnímu vrcholovému pokrytí. Navíc ho umíme vyrobit z jakéhokoliv minimálního řezu.
Ford a Fulkerson se vrací
Zbývá dořešit, kde vzít minimální řez. Řezy z teorie toků jsou takzvané elementární řezy
kde A a B jsou množiny vrcholů takové, že A∪B=V, A∩B=∅, z∈A, s∈B. Každý elementární řez je zs-řezem podle naší definice, ale opačně to platit nemusí. (Můžete si zkusit dokázat, že jsou-li všechny kapacity kladné, je každý minimální zs-řez elementární. Ale potřebovat to nebudeme.)
Připomeňme si důkaz korektnosti Fordova-Fulkersonova algoritmu. Po zastavení algoritmu označíme A množinu všech vrcholu dosažitelných ze zdroje po nenasycených hranách (to jsou jednak hrany, po kterých teče méně než jejich kapacita, a jednak hrany opačné k těm, po nichž něco teče). Pro náš příklad toku a sítě to vyjde takto:
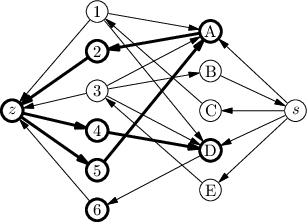
(Tučné hrany jsou ty nenasycené – všimněte si, že pro síť s jednotkovými kapacitami to jsou hrany s tokem 0 a hrany opačné k těm s tokem 1. Tučné vrcholy leží v A.) Zdroj leží v A a jelikož se algoritmus zastavil, spotřebič tam neleží. Položíme-li B=V\A, dostaneme následující elementární řež E(A,B):
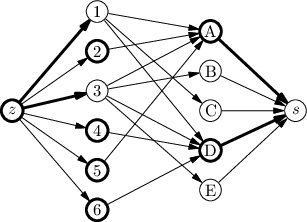
Každá hrana E(A,B) přitom musí být nasycená. Takže po hranách z A do B teče tolik, co kapacita, a po hranách z B do A neteče nic. Velikost toku je tedy rovna kapacitě řezu. A jelikož každý tok je shora omezen každým řezem, musí být tento tok maximální a řez minimální.
Množiny A a B můžeme snadno najít v čase O(m), stejně tak hrany E(A,B). Tento řez stačí převést na okrajový, a pak z něj vyrobit vrcholové pokrytí.
Konverzi řezu na okrajový si dokonce můžeme odpustit – ukážeme, že E(A,B) je sám okrajový. Sporem: Co by se stalo, kdyby nějaká hrana ab∈E(A,B) nebyla okrajová? Vrchol a je dosažitelný po nenasycených hranách, vrchol b nikoliv. Tím pádem hrana ab je nasycená, takže po ní teče 1. Tato 1 ovšem do a mohla přitéci jen ze zdroje, takže za je také nasycená. Aby bylo a∈A, musí do a vést nějaká další nenasycená hrana pa z vrcholu p v pravé partitě. Ta v původní síti nebyla (všechny hrany vedly zleva doprava), takže se musela stát nenasycenou díky tomu, že po opačné hraně ap něco teče. Ale to by znamenalo, že z a odtékají aspoň 2 jednotky, které neměly kudy přitéci. Hle, spor.
Rozmyslete si, že vrcholové pokrytí můžeme popsat prostě tak, že obsahuje vrcholy levé partity, které leží v B, a vrcholy pravé partity, které leží v A.
Závěrem
Pro mřížku R×S políček jsme vyrobili bipartitní graf s R+S vrcholy a O(RS) hranami. Z něj přidáním zdroje a spotřebiče a R+S hran síť. Obojí stihneme v čase O(m+n), kde n∈O(R+S) a m∈O(RS) je počet vrcholů a hran sítě.
Fordův-Fulkresonův algoritmus doběhne v čase O(nm) = O((R+S)·RS). Nalezení minimálního řezu a jeho převod na minimální vrcholové pokrytí se do tohoto času pohodlně vejdou. Pokud by mřížka byla přibližně čtvercová, mohli bychom výraz zjednodušit na O(P3), kde R, S∈O(P).
Časovou složitost můžeme zlepšit použitím rychlejšího algoritmu na toky, například Dinicovým algoritmem se dostaneme na složitost O(√n·m) = O(P2.5).
A mimochodem … také jsme vlastně dokázali zmíněnou Königovu větu ☺
 37-1-S Návrat virtuálního stroje (Zadání)
37-1-S Návrat virtuálního stroje (Zadání)
Seriál lze odevzdávat za snížený počet bodů až do konce školního roku. Řešitelům, kteří už první sérii odevzdali, rozešleme vzorové řešení napřímo. Pokud chceš tuto sérii přeskočit a začít řešit další díl, můžeš si o vzorové řešení napsat na ksp@mff.cuni.cz.