Druhá série třicátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 37-2-1: Urychlovač částic
- 37-2-2: Pohoří plné jezer
- 37-2-3: Chov ovcí
- 37-2-4: HTTP bludiště
- 37-2-S: Lexery útočí
- 37-2-X1: Intervalové většiny
 37-2-1 Urychlovač částic (Zadání)
37-2-1 Urychlovač částic (Zadání)
K řešení úlohy můžeme použít dynamické programování. To trochu připomíná důkaz indukcí – Nejprve triviálně vyřešíme nějakou zmenšenou verzi problému. Poté toto řešení nějak rozšíříme, aby řešilo o něco větší verzi problému, poté ještě větší, a tak dále, dokud se nedostaneme k původnímu problému.
Úlohu si nejprve zjednodušíme tak, že budeme chtít jen spočítat součet úžasností v nejlepší posloupnosti přeměn, aniž bychom tuto posloupnost nalezli. Zato řešení spočítáme pro každý cílový prvek, ne jen pro hélium.
Nejprve musíme najít nějaký způsob, jak úlohu zmenšit. Nabízí se tři možnosti:
- Vyřešit úlohu pro menší počet prvků P.
- Vyřešit úlohu pro menší počet nastavení urychlovače N.
- Vyřešit úlohu pro menší počet provedených přeměn K.
První dvě možnosti sice vypadají lákavě, ale není snadné existující řešení rozšířit přidáním prvku nebo nastavení. Zaměříme se tedy na třetí možnost.
Součet úžasností nejlepší posloupnosti k přeměn, která z vodíku vyrobí prvek s protonovým číslem p, si označíme jako dp[k][p]. Pokud taková posloupnost neexistuje, pak bude dp[k][p] = -∞. Naším konečným úkolem je spočítat dp[K][2].
Pro k = 0 úlohu vyřešíme snadno. Pomocí nula přeměn můžeme získat jen vodík, a to se součtem úžasností přeměn 0, proto bude dp[0][1] = 0. Ostatní prvky vůbec vyrobit nemůžeme, tedy pro p ≥ 2 bude dp[0][p] = -∞.
Teď si musíme rozmyslet, jak řešení pro k přeměn rozšířit na řešení pro k + 1 přeměn. Posloupnost k + 1 přeměn získáme tak, že vezmeme posloupnost k přeměn a přidáme další přeměnu. Pro každý prvek se tedy podíváme na všechna nastavení n, která ho umí vyrobit. Pro každé z nich spočítáme součet jeho úžasnosti a úžasnosti nejlepší posloupnosti délky k-1, která vyrobí potřebný vstupní prvek. Úžasnost chceme maximalizovat, takže z těchto potenciálních úžasností vezmeme tu největší. Získali jsme tedy tento vzorec:
Maximum z prázdné množiny definujeme jako -∞.
Získali jsme tím tento jednoduchý algoritmus:
- Pro k od 0 do K:
- Pro p od 1 do P:
- dp[k][p] ←-∞
- dp[0][1] ←0
- Pro k od 1 do K:
- Pro p od 1 do P:
- Pro každé nastavení n vytvářející prvek p:
- dp[k][p] ←max(dp[k][p], dp[k-1][an] + un)
Pro implementaci tohoto algoritmu potřebujeme umět rychle najít všechna nastavení, která vyrobí daný prvek. Nastavení bychom si mohli snadno předem roztřídit, ale snazší řešení je pro každé k jednou projít všechna nastavení a každé započítat do správné hodnoty dp:
- Pro k od 0 do K:
- Pro p od 1 do P:
- dp[k][p] ←-∞
- dp[0][1] ←0
- Pro k od 1 do K:
- Pro n od 1 do N:
- dp[k][vn] ←max(dp[k][p], dp[k-1][an] + un)
Tento algoritmus bude mít časovou složitost O(KP + KN), paměťovou O(KP + N).
Ještě musíme tento algoritmus upravit tak, aby kromě spočítání úžasnosti nejlepšího řešení toto řešení také našel. Stačí, když si u každé hodnoty v dp navíc zapamatujeme, pomocí kterého posledního nastavení jsme jí dosáhli. To nám umožní postupně posloupnost přeměn zrekonstruovat odzadu dopředu.
 37-2-2 Pohoří plné jezer (Zadání)
37-2-2 Pohoří plné jezer (Zadání)
Pojďme nejprve rozebrat, jak zaručeně určit, kolik maximálně vody se může nacházet na jednom vybraném políčku pohoří.
Víme, že se voda udrží na nějakém políčku pouze v případě, že nedokáže nějakou cestou přetéct přes okraj pohoří.
Uvažme potom libovolné políčko p. Nechť hp je nejvyšší možná nadmořská výška hladiny vody nacházející se na tomto políčku a odpovídá součtu jeho výšky a výšky největšího sloupce vody, který na něm ještě může ležet.
Všimneme si, že nám libovolná cesta z p na okraj pohoří poskytuje horní odhad maximálního množství zadržené vody na políčku p. Je-li totiž výška nejvyššího políčka na cestě z p na okraj rovna m, nemůže hp tuto výšku nikdy přesáhnout. To platí, jinak by v takovém případě existovala cesta, na které by se nenacházela žádná překážka vysoká, jako je nadmořská výška hladiny vody na políčku p, a nějaká voda by musela nutně odtéci.
Pokud bychom pro políčko p vybrali ze všech možných cest na okraj (těch bude konečně mnoho), takovou cestu, pro kterou platí, že je maximum z jejich políček nejnižší, získali bychom nejnižší a tedy i nejpřesnější horní odhad.
Dokažme, že tento odhad odpovídá skutečnému množství zadržené vody.
Předpokládejme pro spor, že je maximální množství zadržené vody na políčku p nižší než náš odhad. Pokud bychom potom na prázdné políčko p nalili množství vody odpovídající hornímu odhadu a maximální množství zadržené zadržené vody by bylo nižší, musela by nějaká voda nutně odtéci z políčka p pryč. Víme však, že voda může odtéci jedině po nějaké cestě. Na takové cestě by ovšem muselo být každé políčko menší, než nadmořská výška hladiny, jinak by byl někde proud vody zadržen. Nalezli jsme tedy cestu z vybraného políčka na okraj pohoří, jejíž maximum je menší než náš nejnižší horní odhad. To je ovšem spor s předpokladem, že jsme původně nalezli takovou cestu, jejíž nejvyšší políčko je nejnižší možné.
Máme tedy zaručený postup, jak nalézt pro libovolné políčko maximální množství vody, které může zadržet. Stačí nalézt pro dotyčné políčko takovou cestu na okraj, jejíž nejvyšší políčko je nejnižší možné.
Výška nejvyššího políčka této cesty pak bude odpovídat nadmořské výšce hladiny na políčku p a odečtením výšky samotného políčka získáme výšku vodního sloupu a tedy i jeho objem.
Pro větší přehlednost textu budeme cestu, jejíž nejvyšší políčko je nejmenší možné, odteď označovat jako nejnižší. Dále budeme hodnotu nejvyššího políčka libovolné cesty nazývat její výškou.
Reprezentace pomocí vhodného grafu
Doposud jsme pracovali s grafem, ve kterém jsou trochu neobvykle ohodnoceny vrcholy místo hran. Navíc pracujeme s okrajem pohoří, který byl dosud v našich úvahách zastoupen všemi poličky na obvodu pohoří.
Pokusme se tedy, ještě než se pustíme do samotné řešení, problém lehce přeformulovat do takové podoby, o které se nám bude lépe přemýšlet. To uděláme reprezentací pohoří pomocí vhodného grafu.
Tento graf bude obsahovat za každé políčko jeden vrchol a každé dva vrcholy budou propojeny hranou, pokud spolu odpovídající políčka sousedí stranou.
Navíc do tohoto grafu zavedeme nový vrchol, který bude představovat okraj pohoří a bude propojen se všemi vrcholy po obvodu pohoří.
Nakonec ohodnotíme každou hranu maximem z hodnot vrcholů, které propojuje. V případě ohodnocení hran vedoucích z vrcholu okraje si můžeme představit, že je hodnota vrcholu okraje rovna nule.
Nahlédneme, že je maximum z hodnot políček na libovolné cestě a maximum z ohodnocení hran na téže cestě v novém grafu totožné.
Problém nalezení nejnižší cesty z políčka p do okraje je tedy ve staré i nové reprezentaci ekvivalentní, jen v nové reprezentaci plyne ohodnocení z jednotlivých hran cesty a ne vrcholů.
Řešení založené na Dijkstrově algoritmu
Nejprve náš problém převedeme do výše uvedené grafové reprezentace. Naším cílem nyní bude pro každý vrchol políčka zjistit výšku nejnižší z něj do okraje vedoucí cesty. K tomu použijeme upravený Dijkstrův algoritmus, který místo délky nejkratších cest z vybraného vrcholu do všech ostatních bude hledat výšku nejnižších cest.
Ten spustíme z vrcholu okraje. Platí totiž, že je kvůli obousměrnosti hran každá nejnižší cesta z vrcholu v do vrcholu okraje zároveň nejnižší cesta vedoucí z okraje do vrcholu v, a naopak.
Pro každý vrchol si budeme v průběhu algoritmu pamatovat, jaká je výška nejnižší aktuálně známé cesty vedoucího z vrcholu okraje. Na počátku bude mít vrchol okraje hodnotu záporného nekonečna a ostatní vrcholy budou ohodnoceny nekonečnem.
Zároveň budeme pro každý vrchol rozlišovat tři stavy. První bude stav odpovídá tomu, že nebyl dosud nalezen. Jakmile vrchol nalezneme, označíme jej jako otevřený a naopak v okamžiku, kdy si budeme jisti s jeho ohodnocením, vrchol označíme jako uzavřený.
Jediný vrchol, který bude na začátku otevřený, bude vrchol okraje. Zbývající vrcholy označíme jako nenalezené.
V každém kroku algoritmu vždy vybereme otevřený vrchol u, do kterého vede cesta s aktuálně nejmenší výškou. Tento vrchol prohlásíme za uzavřený. Následně projdeme jeho otevřené a nenavštívené sousedy.
Všechny nenavštívené sousedy vrcholu u otevřeme. Následně pro každého jeho souseda zjistíme nejnižší známou výšku cesty, který nejprve vede z okraje do vrcholu u a následně vstoupí souseda přes hranu, jež je propojuje. To uděláme tak, že vezmeme maximum z nejnižší známé cesty vedoucí do vrcholu u a ohodnocení hrany, která jej spojuje s aktuálním sousedem. Pokud je tato hodnota nižší, než nejlepší známá cesta vedoucí do tohoto souseda, aktualizujeme ji.
Pojďme dokázat, že na konci běhu algoritmu budeme pro každý vrchol znát výšku nejnižší cesty vedoucí do vrcholu okraje.
Nejprve nahlédneme, že ohodnocení vrcholů, v tom pořadí, v jakém je uzavíráme, nikdy neklesne. To platí, neboť ve chvíli, kdy nějaký vrchol uzavřeme, je jeho ohodnocení nejmenší ze všech ostatních otevřených vrcholů a každé nové ohodnocení, kterým tento vrchol nebo libovolný z ostatních otevřených vrcholů ohodnotí některého ze svých sousedů, bude vyšší nebo stejné.
Dále si všimneme, že každé ohodnocení odpovídá výšce nějakého skutečně existujícího sledu. Rozmysleme si, že lze každý sled zjednodušit na cestu, aniž by došlo k zhoršení hodnocení. Nemůže tedy nastat situace, kdy by algoritmus ohodnotil nějaký vrchol nižší hodnotou, než je výška jeho nejnižší cesty.
Stále ovšem mohl být nějaký vrchol ohodnocen vyšší hodnotou, než je ta správná, případně nemusel být navštíven vůbec. Předpokládejme nyní pro spor, že existuje nějaký vrchol, jehož nalezená hodnota je vyšší než výška nalezené nejnižší cesty, případně nekonečno, protože nebyl dotyčný vrchol vůbec navštíven.
Uvažme libovolnou nejnižší cestu vedoucí z tohoto vrcholu na okraj. Vrcholu na této cestě, jehož ohodnocení odpovídá skutečné výšce nejnižší cesty, říkejme dobrý, jinak dotyčný vrchol nazvěme špatným.
Nejnižší cesta zaručeně obsahuje dobrý vrchol, to je vrchol okraje a špatný vrchol, to je náš vrchol se špatným hodnocením.
Zaměřme se potom na k okraji nejbližší špatný vrchol na této cestě. Ten zaručeně sousedí s dobrým vrcholem, který se nachází blíž k okraji. Protože byl tento dobrý vrchol navštíven, nemohlo se stát, že by nebyl špatný vrchol navštíven. Špatný vrchol tak byl alespoň jednou ohodnocen. Špatné ohodnocení by potom mohl získat jedině tehdy, kdyby byl uzavřen dřív než sousední dobrý vrchol, jinak by byl správně ohodnocen dobrým vrcholem. Na nejnižší cestě je skutečné ohodnocení neklesající a ohodnocení špatného vrcholu je ostře větší než to skutečné, takže byl špatný vrchol uzavřen s větší hodnotou a tedy i později než dobrý vrchol.
Potom by ale dobrý vrchol tento vrchol ohodnotil správnou výškou a musel by být též dobrým vrcholem. Došli jsme k hledanému sporu.
Algoritmus opravdu nalezne pro každý vrchol hledanou výšku do něj vedoucí cesty.
Pojďme zrekapitulovat celé řešení.
Nejprve v O(RS) postavíme grafovou reprezentaci pohoří, následně spustíme upravený Dijkstrův algoritmus a získáme pro každé políčko maximální možný objem vodního sloupu. Nakonec v O(RS) objemy sečteme.
Pokud Dijkstrův algoritmus implementujeme pomocí binární haldy, dosáhneme časové složitosti O(RS log RS) a paměťové O(RS).
Dodejme, že není nutné v implementaci stavět celý graf. Taková implementace je třeba v našem vzorovém zdrojovém kódu.
Řešení založené na minimální kostře
Na tuto úlohu existuje ještě jeden pohled, tentokrát založený na minimální kostře.
Platí totiž, že stačí vzít libovolnou minimální kostru našeho grafu a cesta mezi každým vrcholem a vrcholem okraje bude vždy nejnižší.
Toto tvrzení dokážeme sporem. Mějme libovolnou minimální kostru a předpokládejme, že existuje vrchol, pro který platí, že cesta v minimální kostře mezi ním a vrcholem okraje není nejnižší.
Vezměme nyní libovolnou nejnižší cestu do tohoto vrcholu a vyberme z ní ty hrany, které neleží v minimální kostře. Každou z těchto hran zkusíme vložit do minimální kostry. Tím nám vždy vznikne v grafu cyklus. Pokud je v tomto cyklu tato hrana největší, zahodíme ji a zkusíme do grafu vložit další. V případě, že v cyklu existuje nějaká ostře větší hrana než námi přidaná, můžeme ji odstranit, zbavit se cyklu a získat kostru s nižší velikostí. To by byl ovšem spor s předpokladem, že byla původní kostra minimální.
Tato situace tedy nesmí ani jednou nastat. Pokud by ovšem byla každá z vyzkoušených hran největší hranou ve svém cyklu, musela by cesta po hranách v minimální kostře být nejvýše tak vysoká, jako ta nejnižší, což je zase spor s předpokladem, že minimální kostra nejnižší cestu neobsahuje.
V každém případě jsme došli ke sporu, takže je tvrzení dokázáno.
V našem řešení tak nejprve nalezneme v grafové reprezentaci problému nějakým algoritmem minimální kostru.
Ve vzniklé kostře pak již je třeba jen spočítat výšku cesty mezi každým vrcholem a vrcholem okraje a získat tak objem vodního sloupu nad každým políčkem. To lze udělat například pomocí průchodu do šířky začínajícím ve vrcholu okraje.
Časová a paměťová složitost algoritmu závisí na algoritmu použitém k hledání minimální kostry, neboť všechny ostatní kroky jsou lineární v čase i paměti s velikostí pohoří.
Pokud použijeme k hledání minimální kostry algoritmus z kuchařky, získáme řešení běžící v čase O(RS log RS) s paměťovou složitostí O(RS).
Lineární řešení
Úlohu lze řešit ještě trochu rychleji. Použijeme k tomu předchozí řešení založené na minimální kostře.
V něm nás nejvíce zdržovalo samotné hledání minimální kostry, neboť ostatní části algoritmu byly lineární s velikostí pohoří.
Minimální kostru lze sice nalézt pomocí složitějších algoritmů v obecných grafech rychleji, než to umí náš algoritmus z kuchařky, my místo toho nicméně využijeme poznatku, že má náš graf poměrně specifický tvar.
Odpovídá totiž čtvercové mřížce s jedním vrcholem navíc, který je propojen s každým vrcholem na obvodu této mřížky. Takový graf lze nakreslit bez křížení hran a je tedy rovinný.
K nalezení minimální kostry v našem grafu tentokrát použijeme Borůvkův algoritmus. Popíšeme jen jeho průběh, případný důkaz správnosti lze nalézt například v Medvědovo Průvodci labyrintem algoritmů.
Borůvkův algoritmus ve svém průběhu udržuje les, do kterého postupně přidává vhodné hrany z grafu tak dlouho, dokud se z tohoto lesa nestane minimální kostra.
Toto činí v jednotlivých iteracích. Na počátku první iterace udržovaný les odpovídá izolovaným n vrcholům grafu. V každé iteraci potom algoritmus vybere pro každý strom v aktuálním lese nejlehčí hranu, která dotyčný strom propojuje s nějakým jiným stromem lesa. Všechny takové hrany do lesa algoritmus následně přidá.
Pokud jsou hodnoty hran unikátní, nevznikne nám po žádné iteraci přidáním hran cyklus a počet stromů tohoto lesa se pokaždé alespoň dvakrát zmenší, dokud po O(log n) iteracích nevznikne minimální kostra.
My ovšem nemáme unikátnost hran vůbec zaručenou. Můžeme si pomoci tak, že jednotlivé hrany ohodnotíme uspořádanou trojicí, jejíž první hodnota bude původní ohodnocení hrany a druhé dvě budou odpovídat vrcholům, mezi kterými hrana vede. Takové ohodnocení hran již bude zaručeně unikátní. Hodnoty hran budeme porovnávat lexikograficky.
Borůvkův algoritmus dále upravíme, aby každý strom lesa udržoval kontrahovaný do jednoho vrcholu. Iterace v takto upraveném grafu bude vypadat tak, že si každý vrchol vybere nejlehčí incidentní hranu, tyto hrany algoritmus zkontrahuje a zapamatuje si, že patří do minimální kostry.
Popišme, jak provést rychle potřebné kontrahování.
Nejprve prohledáme les vzniklý po první části iterace a přiřadíme každému vrcholu číslo komponenty, v níž se nachází.
Následně přečíslujeme hrany podle čísel komponent.
Hrany spojující vrcholy v téže komponentě poté přečíslujeme zpět (informace o vrcholech, které hrany na začátku propojovaly jsou díky naší úpravě již obsaženy v jejich ohodnocení) a přidáme je do seznamu hran minimální kostry. Ve zbytku algoritmu s nimi již nebudeme pracovat.
Zbyly nám jen hrany spojující jednotlivé stromy, nicméně následkem přečíslování mohou být některé z nich násobné. Zbavit se jich můžeme lexikografickým přihrádkovým tříděním. Pomocí něj dostaneme násobné hrany k sobě. Nyní stačí projít posloupnost hran a z každého úseku násobných hran ponechat pouze tu s nejmenší hodnotou.
Pojďme určit, jakou bude mít takto upravený Borůvkův algoritmus na rovinných grafech časovou složitost.
Zkusme nejprve odhadnout, s kolika nejvýše hranami náš algoritmus bude v jednotlivých iteracích pracovat.
K tomu využijeme dvou užitečných vlastností rovinných grafů. Jednak platí, že rovinný graf zůstane po každém kontrahování hran nadále rovinný. Pro každý rovinný graf o n vrcholech navíc platí, že obsahuje méně než 3n hran.
Z předchozích poznatků plyne, že v každé iteraci pracujeme s lineárním počtem hran vzhledem k počtu vrcholů. Přihrádkové třídění tak bude běžet v lineárním čase vzhledem k počtu vrcholů a tedy i hran. Stejně rychlé budou i zbylé části iterace.
Celkovou časovou složitost získáme sečtením počtu operací přes jednotlivé iterace. Jejich počet v každé iteraci shora odhadneme pomocí horního odhadu počtu hran, to je trojnásobek počtu vrcholů, násobený nějakou konstantou. Víme, že se počet vrcholů v každé iteraci alespoň dvakrát zmenší. Tím dostáváme pro graf o n vrcholech geometrickou posloupnost, která se sečte na O(n).
Protože náš graf obsahuje celkem O(RS) vrcholů, bude výsledná časová složitost O(RS), což je asymptoticky optimální.
 37-2-3 Chov ovcí (Zadání)
37-2-3 Chov ovcí (Zadání)
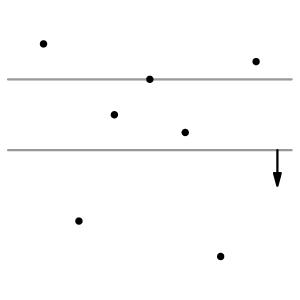
Pojďme najít osově zarovnaný čtverec A ×A s právě K body uvnitř. Na to použijme známou geometrickou techniku, totiž zametání roviny. Všimněme si totiž, že pokud najdeme libovolný čtverec odpovídající naším požadavkům, tak ho můžeme posouvat doleva, dokud by posunutí nepřidalo nebo neodebralo nějaký bod. To samé platí pro posunutí nahoru. Tedy alespoň jedna z vertikálních hran bude (nebo těsně nebude) mít na sobě bod. A to samé platí pro jednu z horizontálních.
A jak na to? Budeme si udržovat pás výšky A, který bude obsahovat všechny body se souřadnicemi mezi yp a yp + A. Tímto pásem budeme zametat rovinu a pro každou pozici pás zkoušet hledat čtverec, který má horizontální hrany na pásu. V předchozím odstavci jsme zdůvodnili, že nám stačí uvažovat pouze pozice čtverce, kde na jedné hraně těsně bude, nebo nebude bod. Tedy zajímavé situace nastávají pouze, když nám bod do pásu přibude nebo vypadne.
A tedy pro každou takovouto pozici pásu stačí vyzkoušet všechny možné pozice čtverce. Pokud si aktuální body v pásu budeme udržovat v seřazené podle x (sekundárně podle y) v binárním vyhledávacím stromě, stačí najít bod s souřadnicí x splňující: Čtverec s levým horním rohem (yp, x) obsahuje K bodů. (Zase použijeme argument s posunutím.)
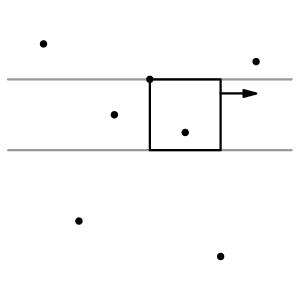
A jak najdeme daný čtverec? Projdeme všechny body v pásu. – Pokud má čtverec začínat na souřadnici xi (kde i je pořadí bodu v BVS), pak aby měl K bodů, musí:
- xi je první bod s takovouto souřadnicí: xi-1 < xi (Jinak bychom část bodů s touto souřadnicí vzali a jinou ne.)
- Obsahovat následujících k bodů: xi+k-1 ≤ xi + A (Všechny na předchozích indexech mají větší x.)
- Zbylé body neobsahovat: xi+k > xi + A (Všechny následující body jsou větší.)
Časovou složitost určíme následovně: Pozic pásu je O(N), pro každou přidáváme bod do binárního vyhledávacího stromu (O(log N)) a zkoušíme všechny pozice čtverců (O(N)). Celkem O(N(log N + N)) = O(N2).
Zrychlujeme
Na poslední zrychlení si všimněme, že pokud vkládáme nebo odstraňujeme bod do našeho pásu, tak toho nově nalezený čtverec musí využívat. Jinak bychom ho nalezli už dřív. Proto stačí v našem binárním vyhledávacím stromě K pozic doleva a K doprava od našeho přidaného (odstraněného) bodu. Navíc ale potřebujeme do BVS přidat velikosti podstromů, abychom mohli v něm rychle najít bod na daném indexu.
Nicméně si musíme dát pozor na případ, kdy více bodů má stejnou y-novou souřadnici. Pro předchozí řešení jsme mohli všechny body přidat nebo odebrat naráz a poté projít celý strom. Něco podobného uděláme i zde, jen musíme být opatrnější. Nejdřív si všechna přidání se stejnou souřadnicí seskupíme. Totéž pro všechna odebrání.
Při přidávání skupiny bodů nejdřív všechny body přidáme, a potom si najdeme jejich pozice ve binárním vyhledávacím stromě. Pokud body odebíráme, budeme si vyhledávat pozice, na kterých by ve výsledném stromě byly, kdybychom je tam nechali. (Tedy index nejbližšího většího prvku.) Poté akorát zkontrolujeme okolí nalezené každé pozice.
- události ← {Přidej bod i, v čase yi} ∪{Odeber bod i, v čase yi+A}
- seřaď(události) ◁ O(N log N)
- seskup(události) ◁ O(N)
- body ← BVS()
- Pro každou událost u ∈ události: ◁ O(U)
- Pokud u je přidání:
- Pro b ∈ u.body: ◁ O(Uk)
- body.přidej(b) ◁ O(log N)
- Pro b ∈ u.body: ◁ O(Uk)
- ib ← body.find(b) ◁ O(log N)
- Jinak u je odebrání:
- Pro b ∈ u.body: ◁ O(Uk)
- body.odeber(u.bod) ◁ O(log N)
- Pro b ∈ u.body: ◁ O(Uk)
- ib ← body.nejbližší_větší(u.bod) ◁ O(log N)
- Pro b ∈ u.body: ◁ O(Uk)
- tb ← body.podposloupnost(ib-k, ib+k+1) ◁ tb – testované body, O(log N + K)
- Pro všechna 1 ≤ j ≤ 2k+1: ◁ O(K)
- Pokud tb[j-1] < tb[j] a tb[j+k-1] ≤ tb[j] + A < tb[j+k]:
- Našli jsme čtverec.
Kde U je počet událostí a Uk počet bodů v k-té události. Pro každý bod děláme O(log N + K) operací, takže naše nové časová složitost bude O(N(log N + K)) = O(NK + N log N).
Znovu zrychlujeme
Nyní ukážeme ještě o něco rychlejší řešení od Erika Ježka.
Nejdříve převeďme problém na trochu jiný: Body nahradíme za čtverce se stranami A×A a jejich pravé dolní rohy budou na souřadnicích původního bodu. Nyní hledáme bod ℓ, který se vyskytuje v právě K čtvercích. Nahlédněme, že pokud ℓ leží ve čtverci odpovídajícímu bodu p, pak v původním příkladě čtverec s levým horním rohem v ℓ obsahoval bod p.
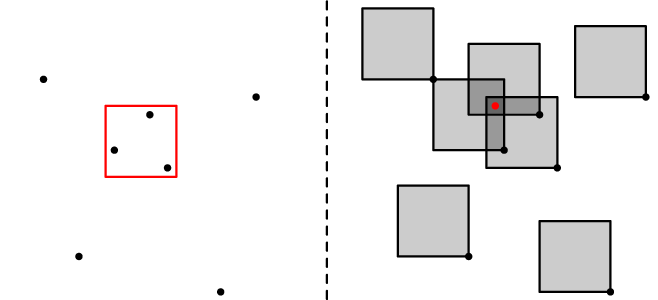
Následně budeme chtít tyto čtverce zamést podle y a udržovat si počty čtverců. Opět si všimněme, že se změny dějí pouze na souřadnicích xi a xi-A pro každý bod (xi, yi) na vstupu. Tyto x-ové souřadnice si seřaďme, čímž nám vznikne dělení na intervaly. Vzhledem k tomu, že uvnitř intervalů nejsou žádné změny, tak nám stačí si udržovat počet čtverců na každém intervalu.
Poté zametejme rovinu podle y a vždy, když narazíme na nějaký čtverec, tak odpovídající úsek intervalů zvedněme o 1. Když nějaký čtverec opustíme, tak odpovídající úsek intervalů snižme o 1. Na toto se hodí líný intervalový strom. A jak zjistit, zdali máme interval s K čtverci? Vzhledem k tomu, že vždy zvedáme o 1, stačí se po každém novém čtverci zeptat na maximum přes celý strom. Pokud je rovné K, tak jsme našli výsledek. A vyšší než K určitě nikdy nebude, protože bychom před tím našli K.
Seřazení na začátku a intervalový strom zaberou dohromady O(N log N) času a O(N) paměti.
Protipříklad
Bohužel předchozí řešení funguje jen, pokud zadané body mají různé y-nové souřadnice. Např. pro v následující konfiguraci bodů s K=3 najde falešný výsledek:

A jakmile připustíme, že K není maximum, nejsme schopní najít v intervalovém stromě i opravdové K.
A co si z toho vzít? Častokrát pro omezenější a omezenější kategorie vstupů jsme schopní konstruovat lepší a lepší algoritmy. Důležité je se ptát, jestli vyřešíme stále zajímavou část vstupů (jako Erikovo řešení), nebo naše vstupy už jsou vzácné a řešení spíše k ničemu.
Níže najdete ochutnávku dalších algoritmů, kde omezení vstupů výrazně vylepší časovou složitost:
- Řazení: Pokud předpokládáme, že prvky na vstupu lze pouze porovnávat, je potřeba čas Ω(n log n). Ovšem celá čísla v rozsahu 1,…,r jdou seřadit přihrádkovým tříděním v čase O(n + r).
- Splnitelnost logické formule: Obecný případ nikdo neumí řešit v polynomiálním čase, ale variantu 2-SAT lze řešit v O(n).
- Celočíselné datové struktury: Zde uvedeme např. van Emde-Boasovy Stromy a Q-haldy.
 37-2-4 HTTP bludiště (Zadání)
37-2-4 HTTP bludiště (Zadání)
1. úkol: Autentikace
V prvním úkolu na nás server vybafne 401 Unauthorized. Ale naštěstí
v poli hlavičky X-Hint napoví, jaké je správné heslo. Tak si vymyslíme
nějaké uživatelské jméno (třeba hroch), použijeme autentikační metodu
Basic a zkusíme to znovu.
Tak jednoduché to ovšem není: server nás vyžene s 403 Forbidden
a vysvětlením, že právo stáhnout si heslo má jedině root (správce
serveru). Zkusíme tedy změnit uživatelské jméno na root a server
spokojeně pošle soubor typu text/plain s klíčem.

2. úkol: Formulář
Server nás nejdřív přesměruje (307 Temporary Redirect) na .../form.cgi?task=37-2-4&what=key
a následně nám vysvětlí, že používáme špatnou metodu (405 Method Not Allowed).
Naštěstí, jak standard káže, připojí Allow:, kde prozradí, že jediná podporovaná
metoda je POST, a vysvětlí že očekává POST webového formuláře.
Podle kuchařky máme tedy odeslat obsah formuláře jako Content-Type: application/x-www-form-urlencoded
(jinak dostaneme 415 Unsupported Media Type). Potom nás server navede odpovědí 422 Unprocessable Content,
že vyžaduje argumenty task a what. Zkopírujeme je tedy z původního URL a server odpoví
přesměrováním 303 See Other na textový soubor s klíčem.
Mimochodem, kdybyste místo what=key poslali what=hint, doslechli
byste se, že nápovědy nevydáváme :)
3. úkol: PUT
Ve třetím úkolu se opět dozvíme, že metoda GET není podporována.
Tentokrát máme použít PUT a nahrát tak své jméno.
Tělo musí mít textový Content-Type, jinak ho server odmítne s 415 Unsupported Media Type.
Musíme uvést délku těla (jinak 411 Length Required) a ta nesmí být větší než 1000 bytů
(nechceme-li dostat 413 Request Entity Too Large).
V odpovědi na PUT obdržíme heslo.
4. úkol: Varianty
Zde na první pokus server odpoví 300 Multiple Choices a nabídne nám
výběr z několika variant: minotauros.gif, minotauros.xml a minotauros.png.
Požádáme-li o GIF, server ho odmítne vydat s 451 Unavailable for Legal Reasons
a odkazem na známou kontroverzi kolem
softwarových patentů na kompresi LZW.
Odmítnutí je nicméně doprovázeno omluvou a nabídkou kompenzace ve výši jednoho dolaru.
A vskutku: v hlavičce odpovědi objevíme X-Coin: $1. Heslo ovšem nikde.
Tak zkusíme XML a dostaneme dokument ve formátu XML, v němž je očividný
element <klic> s očekávaným obsahem.
Intermezzo: Odznáček
Co kdybychom zkusili ještě PNG? To by nás s omluvou, že dokument byl dočasně přesunut,
přesměrovalo (307 Temporary Redirect) na .../img/1/minotauros.png. Tam
bychom dostali přesměrování na .../img/2/... atd. Kdo si to vyzkoušel, zjistil,
že server umí libovolně velká čísla, takže posloupnost přesměrování je nejspíš nekonečná.
Pokud máme hravou náladu, zkusíme se podívat na konec nekonečné posloupnosti:
místo čísla napíšeme nekonecno, nekonečno, infinity nebo ∞ (v UTF-8).
To překvapivě funguje a obdržíme 303 Found something at infinity s Location:
odkazující na URL typu mailto: – požadavek na odeslání mailu organizátorům,
jehož předmětem si říkáme o odznáček.
5. úkol: Pigzip
V tomto úkolu nám server hned pošle klíč. Jenže ouha, klíč je ve formátu application/x-pigzip,
zkomprimovaný do řetězce 42. X-See-Also nám prozradí, že Pigzip je narážka na dávný
linuxový comics Hackles, kde prasátko Preston vyvine nový kompresní algoritmus, schopný cokoliv zkomprimovat do 3 bajtů.
Jen má zatím potíže s dekompresí …
Ani my nedokážeme Pigzip dekomprimovat, tak si všimneme, že v hlavičce odpovědi je ještě
Vary: Accept a Accept-Ranges: bytes. To druhé nás ještě nezajímá, ale první naznačuje,
že server nejspíš podporuje domlouvání se na typu dat.
Nevíme ovšem, o jaký typ si říci. Accept: text/plain ani nic podobného server není
ochoten splnit. Co tedy chceme? Inu, cokoliv kromě Pigzipu. To se dá říci jako
Accept: */*;q=1.0, application/x-pigzip;q=0.9.
Server málem odpoví s Content-Type: application/x-ksp-key, ale v poslední
chvíli se zarazí, že je odpověď moc dlouhá (413 Request Entity Too Large) a dodá,
že nekonečné soubory neposílá. Není divu, že na to potřebovali Pigzip …
Vzpomeneme si tedy na Accept-Ranges a zkusíme poslat požadavek na nějaký interval,
třeba Range: bytes=0-1000. Dostaneme 206 Partial Content s tělem, v němž
se opakují řádky klic=.... Vida.
Dodejme, že kdybychom si řekli o interval delší než 1 KB,
dostali bychom také status 413.
6. úkol: Ach ty keše
V tomto úkolu nám server ochotně pošle požadovaný soubor. Jenže v něm je napsáno,
že klíč zatím nebyl nastaven a máme to zkusit znovu po vydání 2. série. Last-Modified
nám prozradí, že tento soubor opravdu vznikl před vydáním série, a podle přítomnosti Age
poznáme, že mezi námi a serverem stojí keš, která si soubor zapamatovala. A pamatovat si ho
nejspíš bude dost dlouho, protože uvedené Expires je v daleké budoucnosti.
Naštěstí můžeme keši pomocí Cache-Control: no-cache nebo max-age nařídit,
aby sehnala čerstvý obsah. V něm už klíč cinká.
7. úkol: Vhoďte minci
V posledním úkolu nám server odmítá vydat klíč, dokud nezaplatíme:
402 Payment Required. A prý máme vložit minci. Tak si vzpomeneme,
že ve 4. úkolu jsme jednu minci získali. Pošleme tedy s požadavkem
X-Coin: $1 a hle – je tu klíč.
Závěrem
Vzorový program si vystačí s pythoní knihovnou requests, která všechny potřebné
části HTTP buď přímo umí, nebo si je jde objednat ručním nastavením hlavičky.
Úloha je inspirovaná Medvědovou dávnou úlohou v soutěži Po drátě. Děkujeme Jefovi Poskanzerovi za minimalistický webový server thttpd, z nějž naše implementace vychází.
 37-2-X1 Intervalové většiny (Zadání)
37-2-X1 Intervalové většiny (Zadání)
Začněme užitečným pozorováním. Mějme libovolný úsek posloupnosti a rozdělme jej na několik libovolně dlouhých částí. Potom platí, že kdykoliv má nějaká barva v celém úseku nadpoloviční většinu, je tato barva zastoupena v nadpoloviční většině i v alespoň jedné z těchto částí.
To platí, neboť kdykoliv má nějaká barva nadpoloviční většinu, lze její výskyty spárovat s výskyty ostatních barev v posloupnosti a navíc zůstane nějaký výskyt vždy nespárován. Pokud ovšem nemá barva ani v jedné části většinu, lze spárovat všechny její výskyty.
Víme tedy, že kdykoliv má nějaká barva v libovolném úseku posloupnosti nadpoloviční většinu, můžeme úsek libovolně nasekat na různě velké části a barva vždy bude mít nadpoloviční většinu alespoň v jedné z těchto částí. Opačná implikace bohužel neplatí, a pokud obsahuje jedna z částí úseku nějakou barvu v nadpoloviční většině, vůbec nic to neříká o výskytu této barvy ve zbylých částech úseku, a tím pádem ani o výskytu této barvy v celém úseku.
Přesto je toto pozorování velice užitečné. Pokud jsme totiž schopni rozdělit nějaký úsek na k částí, o kterých již víme, zda v nich má nějaká barva nadpoloviční většinu, získáme nejvýše k kandidátů na barvu zastoupenou v nadpoloviční většině, a stačí nám potom již jen ověřit, zda nějaký kandidát nadpoloviční většiny skutečně nabývá.
Na této myšlence budou stát všechna řešení, která si dnes ukážeme. V každém z nich pro vhodně vybrané úseky posloupnosti předpočítáme, zda v nich má nějaká barva nadpoloviční většinu.
Díky tomu budeme schopni složit libovolný dotazovaný úsek z několika předpočítaných, a zjistit tak kandidáty na nadpoloviční většinu. Nejprve si ukážeme řešení běžící v čase O(N log N). V něm budeme skládat každý dotazovaný úsek z nejvýše dvou předpočítaných úseků. V dalších, rychlejších řešeních už budeme potřebovat předpočítaných úseků více.
Jakmile získáme všechny kandidáty, ověříme pro každého z nich, zda nabývá nějaký z nich nadpoloviční většinu a případně tuto většinu vrátíme.
Protože jsme limitováni časem O(1) na dotaz, bude nezbytné v tomto čase zvládnout nejen rozdělení úseku na jednotlivé části, ale i ověření četností kandidátů.
Přečíslování barev
Ze zadání víme, že čísla barev mohou být poměrně vysoká. Nám by se nicméně hodilo, aby jejich velikosti byly v rozsahu řádově tak velkém, jako je jejich počet. Potom by bylo například možné čísly barev indexovat pole o velikosti O(N).
Přečíslování provedeme takto: ke každé barvě si poznamenáme její původní pozici, pak dvojice (barva, pozice) setřídíme podle barvy. Následně barvám přiřadíme nové číslo podle pořadí, v jakém se objeví, a tato nová čísla zaneseme zpět na původní pozice. Zároveň si vytvoříme pole, které mapuje nové číslo zpět na původní hodnotu barvy.
Předvýpočet a následné intervalové dotazy budeme ve všech popsaných řešeních provádět na získané přečíslované posloupnosti, případný výsledek přečíslujeme využitím pomocného pole mapujícího barvy v O(1) zpět.
Předpokládejme po zbytek řešení, že mají čísla velikost O(Nk) pro nějakou konstantu k. Můžeme potom použít přihrádkové třídění. Celková časová složitost přečíslování tak bude O(N).
Nalezení kandidátů
Naším úkolem nyní bude přepočítat pro vhodně vybrané úseky posloupnosti, zda v nich má nějaká barva nadpoloviční většinu tak, aby šel každý úsek složit z předpočítaných částí.
Představme si nejprve, že je posloupnost rozdělena v polovině a příchozí dotaz prochází skrz tuto polovinu. Každý takový dotaz lze složit ze sufixu první poloviny posloupnosti a prefixu druhé poloviny posloupnosti.
Pokud bychom tedy pro všechny sufixy první poloviny posloupnosti a prefixy druhé poloviny posloupnosti předpočítali jejich většiny, byli bychom schopni složit každý intervalový dotaz procházející přes střed.
Protože dotazované úseky obecně přes střed procházet nemusí, vybudujeme rekurzivně datové struktury stejného typu zvlášť pro levou a pro pravou polovinu.
Pojďme rozebrat, jak rychle předpočítat prefixové či sufixové většiny v nějakém úseku. Postup budeme popisovat jen pro prefixy, postup pro sufixy je analogický.
Založíme si dvě pomocná pole, která budou indexovaná barvami. To první bude sloužit jako počítadlo a to druhé si bude pro každou barvu pamatovat index posledního navštíveného výskytu. Dále si budeme udržovat barvu s největším zastoupením v aktuálním úseku. Pokud je takových barev více, stačí si pamatovat jednu z nich.
Budeme postupně rozšiřovat doprava prefix úseku a pokaždé zjistíme, zda je v něm nějaká barva zastoupena v nadpoloviční většině.
Při rozšíření prefixu aktualizujeme pole posledních navštívených výskytů barev. Dále zvýšíme počítadlo nově přidané barvy o jedna. Pokud četnost barvy překonala aktuální maximum, prohlásíme ji za nové maximum. Následně zkontrolujeme, zda je aktuálně nejčetnější barva zastoupena v nadpoloviční většině, a případně ji uložíme. Připíšeme k ní i poslední navštívený výskyt barvy, v budoucnu se nám tato informace bude hodit.
Na konci nesmíme zapomenout počítadlo zase vynulovat. To lze udělat opětovným průchodem úseku, nicméně tentokrát budeme jen nulovat barvy, na které v průběhu narazíme.
Tímto postupem předpočítáme všechny potřebné prefixy a sufixy. Podívejme se nyní na časovou a paměťovou složitost celého výpočtu.
Vraťme se zpět k myšlence rekurzivního dělení vstupu na poloviny. Tuto strukturu si můžeme představit jako binární strom, jehož vrcholy odpovídají úsekům posloupnosti. Tento strom má O(log N) hladin a na každé z nich zpracujeme všech N prvků, byť v rámci kratších úseků. Celkový počet operací tak bude O(N log N).
Na každé hladině stromu navíc všechny její úseky zakládají vlastní pomocná pole lineární s jejich délkou, takže každá hladina spotřebuje O(N) paměti a celková paměťová složitost přes všechny hladiny činí O(N log N).
Složení dotazu ze sufixu a prefixu
Nyní jsme schopni složit každý dotazovaný interval z sufixu první poloviny nějakého úseku a prefixu druhé. Pojďme ukázat, jak takový úsek nalézt.
Nabízí se algoritmus, ve kterém nejprve ověříme, zda dotazovaný interval protíná střed, a pokud ano, nalezli jsme hledaný úsek a můžeme složit dotazovaný interval ze sufixu jeho první poloviny a prefixu druhé. Pokud interval střed neprotíná, leží konce intervalu ve stejné polovině a na dotyčnou polovinu zavoláme rekurzivně tentýž algoritmus.
Takový postup určitě funguje, nicméně trvá O(log N), což je pro naše účely příliš pomalé. Zkusme jej urychlit. Nejprve pomocí triku s binárním zápisem souřadnic okrajů zjistíme hloubku této rekurze.
K tomu si představme, že je délka posloupnosti mocninou dvojky. Podívejme se na zápis indexů prvků ve dvojkové soustavě. Všechny prvky v levé polovině začínají nulou a v pravé jedničkou. Úsek protíná střed právě tehdy, když se jeho levý a pravý okraj liší v nejvyšším bitu. Pokud jsou nejvyšší bity pravého a levého okraje totožné, leží ve stejné polovině a zbývající bity zápisů okrajů popisují jejich vzájemné pozice v rámci této poloviny. Nejvyšší bit zápisu proto můžeme zahodit a uplatnit rekurzivně stejný postup.
Tímto způsobem se postupně porovnáváme páry bitů od největšího po nejmenší, dokud nenarazíme na první pár, který se liší.
K tomu se bude hodit binární operace xor. Ta porovnává bity dvou zadaných čísel a vrací jako výsledek číslo, které má na pozici i-tého bitu 1 právě tehdy, když jsou i-té bity obou čísel odlišné.
Souřadnice okraje dotazovaného intervalu proto v konstantním čase vyxorujeme a získáme číslo, které obsahuje výsledky porovnání jednotlivých pozic. Nás zajímá nejlevější pozice, kde se bity čísel liší. Hledáme tedy nejvyšší jedničku tohoto čísla.
Využijeme toho, že nám xor vždy vrátí čísla ve stejném rozsahu, jako je délka posloupnosti, takže si můžeme předpočítat tabulku, jenž pro každé číslo obsahuje pozici jeho nejvyšší jedničky. To můžeme udělat v lineárním čase vyplňováním tabulky od nejmenšího čísla po největší a udržování si největší mocniny dvojky, která je menší nebo rovná aktuálně zpracovávané hodnotě.
Zjistili jsme tedy hloubku rekurze, zbývá nám však nalézt samotný úsek. K tomu využijeme, že společné bity pozic okrajů označují pořadí úseku na dané úrovni rekurze.
Ověření kandidátů
Už tedy umíme zjistit, které dva úseky spojit. Pro každý z nich známe nejčetnější prvek. Zbývá ověřit, jestli některý z nich je nejčetnější i v celém zadaném intervalu.
Zaměřme se tedy na to, jak v konstantním čase pro kandidáta ověřit v zadaném úseku jeho četnost.
Nabízelo by se prostě zjistit přesný počet výskytů kandidáta v zadaném intervalu. To lze v O(1) zjistit pomocí obyčejných prefixových součtů. Pokud bychom si však předpočítali prefixové součty pro každou barvu a vždy pro celou posloupnost, strávili bychom O(N2) předvýpočtem.
Mohli bychom proto využít pozorování, že na jedné hladině rekurze při hledání kandidátů stačí prefixové součty spočítat pro O(log N) různých barev, nicméně to je pro naše účely příliš silné a výsledné řešení by to zbytečně zpomalilo logaritmus-krát.
Uvažme, že vlastně nepotřebujeme vědět, jaká je přesná četnost kandidáta v dotazovaném úseku, ale jen, jestli je počet jeho výskytů větší než polovina délky úseku. Využijeme toho, že pro každého kandidáta známe buď jeho nejlevější nebo nejpravější výskyt.
| d |
| 2 |
| d |
| 2 |
Pokud bychom tedy uměli v konstantním čase přeskočit z i-tého výskytu barvy na j-tý, zvládli bychom ověřit pro kandidáta jeho četnost v konstantním čase. K tomu stačí vytvořit v O(N) pole indexované barvami, jež obsahuje odkazy na pole pozic výskytů dotyčné barvy v rostoucím pořadí.
Zároveň si ke každé barvě v posloupnosti poznamenáme, na jaké pozici v poli své barvy se nachází.
Umíme tedy v O(1) nalézt dva kandidáty i ověřit jejich četnost a časová i paměťová složitost algoritmu je O(N log N), takže jsme splnili požadavky zadání.
Zrychlujeme
Předchozí řešení bylo lineární k počtu předpočítaných úseků. Pokud tedy chceme řešení urychlit, budeme muset změnit, jaké úseky předpočítáváme a jak z nich poté skládáme ty dotazované.
Doposud jsme skládali každý dotazovaný úsek nejvýše ze dvou předpočítaných, pojďme konečně použít při skládání úseků více.
V následující části textu si představíme řešení běžící v čase O(N log log N). Toto řešení však bude poměrně komplikované, proto nejprve vysvětlíme jeho hlavní myšlenky a teprve poté se budeme věnovat jeho jednotlivým částem podrobněji.
Podstata rychlejšího řešení spočívá v rozdělení celé posloupnosti na menší bloky o velikosti Θ(log N).
Příchozí dotazy potom budeme rozlišovat podle toho, zda leží uvnitř jediného bloku tohoto rozdělení, nebo zasahují do několika sousedních bloků.
Pokud nám bude položen dotaz na úsek ležící celý uvnitř nějakého bloku, vyřídíme ho pomocí zvlášť předpočítané datové struktury pro tento blok.
Zajímavější budou dotazy zasahující do více bloků. Každý takový dotaz lze složit popořadě z prefixu bloku, nějakého počtu celých bloků a sufixu bloku.
Prefixy a sufixy bloků si můžeme snadno předpočítat podobně, jako jsme zpracovávali prefixy a sufixy úseků již dříve.
Část dotazovaného intervalu skládající se z celých bloků vyřešíme postavením podobné rekurzivné datové struktury, jakou jsme použili v předchozím řešení na celou posloupnost. Každou část intervalu celých bloků tak složíme z nějakého předpočítaného prefixu a sufixu, které se skládají z celých bloků.
Při skládání úseku si tak nakonec vystačíme vždy s nejvýše čtyřmi úseky. Získáme tak maximálně čtyři různé kandidáty, což bohužel trochu zkomplikuje ověřování jejich četností, ale i s tím si nakonec poradíme.
Dekompozice na bloky podrobněji
Pokud nám bude položen dotaz na úsek ležící celý uvnitř nějakého bloku, vyřídíme ho pomocí předchozího O(N log N) algoritmu, který uplatníme na každý blok zvlášť. Tentokrát nicméně nebudeme pro každý blok přečíslovávat barvy a použijeme pro všechny stejné počítadlo délky O(N).
| N |
| log N |
| N |
| log N |
Pojďme vyřešit případ, kdy dotaz kříží více bloků. Jak již víme, každý dotaz zasahující do více bloků lze složit z prefixu bloku, nějakého počtu celých bloků a sufixu bloku.
Předpočítat prefixy a sufixy bloků již umíme – lze to udělat obdobným způsobem, jakým jsme předpočítali prefixy a sufixy v našem O(N log N) algoritmu. Za každý sufix či prefix si opět mimo případnou nadpoloviční barvu uložíme i její nejpravější či nejlevější výskyt. Všimněme si, že je nyní možné pro oba kandidáty snadno ověřit, zda nabývá některý z nich nadpoloviční většinu v celém dotazovaném úseku. Stačí k tomu využít údaje o nejkrajnějším výskytu a přeskočit o polovinu délky celého úseku v odpovídajícím směru.
Zajímavější bude nalezení a ověřené četnosti kandidátů ve zbylé části úseku, tedy té složené z prefixu a sufixu celých bloků. Bohužel platí, že pokud při dotazu známe kandidáty pro prefix i sufix celých bloků, jejich výskyty nemusí být nutně nejkrajnější v dotazovaném úseku a náš trik se skokem nebude fungovat. Další problém, který je třeba vyřešit, je jak vůbec rychle předpočítat kandidáty pro dotyčné prefixy a sufixy bloků.
S řešením obou problémů nám pomůže nová užitečná datová struktura, kterou si představíme v následujících odstavcích.
Kdykoliv budeme v posloupnosti znát pozici nějakého výskytu libovolné barvy, pomocí této struktury budeme schopni v konstantním čase pro libovolnou jinou pozici ve stejném bloku určit nejbližší výskyt téže barvy směrem doleva a doprava.
Zafixujme si konkrétní barvu a představme si posloupnost nul a jedniček, kde na každé pozici je jednička právě tehdy, když odpovídající pozice původní posloupnosti obsahuje tuto barvu.
Všimněme si, že každý blok této posloupnosti má délku O(log N) a obsahuje pouze nuly a jedničky. Takový blok lze snadno zakódovat jako číslo, které se vejde do konstantního počtu paměťových buněk, což nám umožní provádět s ním základní operace v konstantním čase.
Toho využijeme následovně: jestliže nás zajímá nejbližší výskyt dané barvy vlevo nebo vpravo od nějaké pozice v rámci bloku, znamená to, že hledáme pozici nejbližšího jedničkového bitu vlevo nebo vpravo od odpovídajícího bitu v zakódovaném čísle tohoto bloku.
Tento problém lze vyřešit vhodným použitím bitové masky, čímž se převede na nalezení nejlevějšího nebo nejpravějšího nenulového bitu v číslu. Například pro nalezení nejbližšího nenulového bitu vpravo stačí pomocí masky vynulovat všechny vyšší (významnější) bity než dotazovaný bit a následně v takto upraveném čísle určit nejvýznamnější (nejlevější) nenulový bit.
Analogicky pro nalezení nejbližšího nenulového bitu vlevo vynulujeme všechny méně významné bity než dotazovaný bit a ve výsledném čísle nalezneme nejméně významný nenulový bit.
Pozici nejvýznamnějšího bitu v daném čísle lze nalézt pomocí předpočítané tabulky. Zvolíme-li délku bloků v našem řešení jako k · log N, kde k je kladná konstanta menší nebo rovna jedné, velikost největšího čísla po vymaskování bude 2k log N = Nk ≤ N, tudíž lze použít naši tabulku, kterou jsme používali při nalezení správné úrovně rekurze v předchozím řešení.
Stejně tak by si šlo i předpočítat tabulku pro nalezení nejméně významného bitu,
nicméně to není třeba – máme-li číslo x,
lze snadno pomocí základních operací vytvořit číslo, které obsahuje jen nejméně významný bit a jinak samé nuly.
Rozmyslete si, proč funguje vzorec x & ~(x-1).
Protože se v získaném čísle nachází jediný bit, využijeme k nalezení jeho pozice naši tabulku sloužící k nalezení pozice nejvýznamnějšího bitu.
Umíme tedy v konstantním čase nalézt pro danou cifru v čísle pozici nejbližší jedničky zprava a zleva, nicméně si ještě musíme opatřit čísla kódující jednotlivé bloky, na kterých budeme popsané operace provádět.
To uděláme tak, že si pro každou pozici v posloupnosti předpočítáme číslo, které bude kódovat blok, ve kterém dotyčná pozice leží a které popisuje nulami a jedničkami výskyty barvy nacházející se na této pozici:
Pro každou barvu projdeme seznam pozic jejích výskytů a budeme si udržovat, v jakém bloku se aktuálně nacházíme a jaká je pozice první barvy v rámci seznamu pozic, která se v tomto bloku též nachází. Jakmile zjistíme, že jsme vstoupili do nového bloku, projdeme všechny výskyty z předchozího bloku a sestavíme na základě jejich pozic v rámci bloku číslo, které tento blok kóduje.
Pokud nyní známe výskyt nějaké barvy, můžeme se podívat na číslo, které kóduje výskyty barvy v jeho bloku a poté již nalézt v konstantním čase nejbližší jedničku zleva či zprava pro libovolnou dotazovanou pozici ve stejném bloku.
Předpočítání a nalezení blokových kandidátů
Nyní nám už nic nebrání se naplno zabývat otázkou kandidátů blokové části dotazů.
Připoměnme, že plánujeme postavit podobnou rekurzivní datovou strukturu, jakou jsme použili v předchozím řešení na celou posloupnost, ale tentokrát na posloupnosti bloků.
Pokud tedy například úsek z celých bloků kříží střed posloupnosti bloků, můžeme jej opět složit z jednoho předpočítaného prefixu a sufixu polovin posloupnosti bloků. Jinak rekurzivně uplatníme stejný postup na jednu z polovin posloupnosti.
Nalezení správného blokového prefixu a sufixu můžeme udělat se stejnými bitovými triky jako v O(N log N) řešení.
Zajímavější bude předpočítání jednotlivých prefixů a sufixů. Postup ukážeme opět jen pro prefixy. Během výpočtu si budeme opět ukládat i nejkrajnější výskyty.
Prefixy budeme stejně jako minule postupně rozšiřovat doprava o 1 blok. Při rozšíření využijeme toho, že má-li mít nějaká barva po rozšíření nadpoloviční většinu, je to buď ta, co ji má teď, nebo ta, která tvoří většinu v připojeném bloku.
Zkusme nejprve ověřit, zda většinu prefixu tvoří stejná barva, jako ta, která tvoří většinu v nově připojeném bloku. Využijeme toho, že známe její nejpravější výskyt. Potom můžeme ověřit četnost klasickým způsobem skokem o polovinu posloupnosti dopředu.
Kontrola, zda si barva z prefixu před rozšířením zachovává nadpoloviční četnost, se provede trochu víc komplikovaně.
Nejprve skočíme na další výskyt po nejpravějším výskytu kandidáta v rámci prefixu bloků před rozšířením. Pokud tento výskyt leží v nově připojeném bloku, použijeme blokovou jedničkovou datovou strukturu a nalezneme nejpravější výskyt v rámci nově přidaného bloku. V případě, že tento výskyt leží za připojeným blokem, případně vůbec neexistuje, je nejpravějším výskytem ten, který byl nejpravější v prefixu před rozšířením.
Jakmile známe nejpravější výskyt, ověříme opět četnost tradičním způsobem.
Časová složitost této části předvýpočtu bude:
| N |
| log N |
| N |
| log N |
| N |
| log N |
Ověření kandidátů podruhé
Nyní jsme již schopni každý dotaz složit z až 4 předpočítaných úseků a získali jsme tak až 4 různé kandidáty. Zbývá nám ověřit, zda nějaký z nich skutečně nabývá nadpoloviční většiny v dotazovaném úseku.
Ověření kandidáta pocházejícího z prefixu či sufixu nějakého bloku jsme popsali již dříve - známe jeho krajní výskyt a můžeme tedy zkontrolovat jeho četnost přeskočením o polovinu dotazovaného úseku, stejně, jako v předchozím řešení.
Pro prefixy a sufixy bloků už bude situace trochu zajímavější, protože neznáme nejpravější či nejlevější výskyt kandidáta v celé dotazovaném úseku, nicméně si opět pomůžeme naší bitovou datovou strukturou. Postup ověření ukážeme opět jen pro prefixy bloků, sufixy by se dělaly zrcadlově.
Známe nejpravější výskyt kandidáta v rámci prefixu bloků, zkusme tedy skočit na další výskyt kandidáta vpravo. Pokud neexistuje, případně neleží v sousedním prefixu bloku, známe nejpravější výskyt a můžeme tedy ověřit četnost v rámci celého úseku.
Pokud se nachází tento výskyt v prefixu bloku, známe nějaký výskyt kandidáta v rámci sousedního bloku a pomocí naší jedničkové datové struktury nalézt pro kraj prefixu bloku nejbližší výskyt zleva.
Opět jsme nalezli nejpravější výskyt kandidáta v celém úseku a můžeme ověřit četnost.
Jsme tedy schopni v konstantním čase vyřídit všechny dotazy. Získali jsme tak řešení, které k předvýpočtu potřebuje O(N log log N) času a paměti.
S tím bychom se mohli spokojit, nicméně si ve zbytku tohoto textu ukážeme, jak předvýpočet ještě urychlit.
log log log log ... glo glo glo ...
Všimněme si, že v předchozím řešení nejvíce času zabral předvýpočet na dotazy nacházející se uvnitř jednoho bloku, neboť zbylé části algoritmu běžely v O(N).
Co kdybychom proto místo O(N log N) řešení použili na bloky řešení v čase O(N log log N)? Hle, naše nové řešení běží v čase O(N log log log N). A co kdybychom tedy místo toho použili na bloky toto řešení?
Je patrné, že si do řešení můžeme takto přidávat kolik logů chceme, alespoň dokud je jich konstantní počet. Pojďme na tom proto založit co nejrychlejší algoritmus.
Víceúrovňová bloková dekompozice
Na předchozí úvahu o rekurzivním uplatňování řešení na bloky můžeme nahlížet jako na víceúrovňovou stromovou datovou strukturu.
Na nulté úrovni této struktury se nachází kořen reprezentující celou posloupnost. Z něj vedou hrany do první úrovně, kde se nachází vrcholy reprezentující jednotlivé bloky délky O(log N), na které je naše posloupnost rozložena.
Z každého vrcholu bloku obdobně vedou hrany do vrcholů na druhé úrovni, které reprezentují rozklad daného bloku na bloky velikosti O(log log N). Třetí vrstva pak obsahuje bloky délky O(log log log N), čtvrtá vrstva O(log log log log N) a tak dále.
Potomci každého vrcholu jsou řazeni stejně, jako odpovídající bloky v posloupnosti.
Listy této struktury reprezentují nejdrobnější rozklad posloupnosti, na něž je zavolán náš O(N log N) algoritmus.
Každý dotaz poté vyřizujeme tak, že postupně procházíme od kořene jednotlivé úrovně a hledáme nejmenší blok, který obsahuje celý dotazovaný úsek. Jakmile jej nalezneme, spustíme odpovídající řešení.
K získání co nejrychlejšího řešení se nabízí nastavit této struktuře největší možné množství úrovní, tedy takové, aby bloky na poslední úrovni měly délku jedna. To by mělo za následek, že by počet úrovní nebyl konstantní, takže by nebylo konstantní ani naivní hledání správného bloku průchodem od kořene.
S tím bychom si mohli poradit, nejprve bychom vynutili, aby měly všechny bloky na stejné úrovni stejnou délku. Pokud by poté dotaz zasahoval jen do jednoho bloku na první úrovni, nezáleželo nám na tom, do jakého bloku první úrovně přesně padl. Díky pravidelné struktuře stromu by totiž platilo, že nehledě na blok bude vyřízen na stejné hladině a k vrcholu nejmenšího bloku obsahující celý dotaz povede stejná cesta.
Stačilo by si proto předpočítat tabulku pro všech O(log N · log N) druhů dotazů, a získat tak možnost nalézt hledaný blok v konstantním čase.
Takový postup by vedl na řešení běžící v čase O(N log * N).
My nicméně nebudeme v našem finálním řešení stavět datovou strukturu s nekonstantní hloubkou. Místo toho si vystačíme se strukturou, která má pouze tři úrovně.
Využijeme přitom skutečnosti, že bloky na druhé, tedy nejnižší úrovni mají délku pouze O(log log N). Jejich malá velikost nám umožní na ně uplatnit efektivnější algoritmus než klasický O(N log N), který jsme na bloky na poslední úrovni používali doposud.
Díky tomu nakonec se nakonec dopracujeme k řešení s celkovou časovou složitostí O(N), což je zaručeně optimální.
Lineární řešení
Naše stromová datová struktura tedy bude mít celkem tři úrovně. První dvě úrovně jsme již popsali dříve, takže se ve zbytku textu zaměříme pouze na tu poslední.
O té víme, že se celá skládá z bloků délky O(log log N). Předpokládejme bez újmy na obecnosti, že všechny bloky této úrovně mají stejnou délku d.
Zkusme nyní libovolně přečíslovat barvy v každém bloku čísly 0, 1, …, d-1. To má za následek, že každý blok posloupnosti nyní spadá do jednoho z dd možných druhů bloků.
Protože je d ve srovnání se vstupem velmi malé číslo, nabízí se otázka, kolik takových druhů bloků vlastně existuje. Pokud by byl jejich počet dostatečně malý, mohli bychom si pro každý druh předpočítat všech O(d2) možných dotazů.
Při řešení dotazu na třetí úrovni by pak stačilo zjistit, do jakého druhu spadá blok, ve kterém se dotaz nachází, nalézt odpověď v tabulce pro daný druh a daný dotaz, a tuto odpověď následně přečíslovat zpět.
Na této myšlence bude stát naše řešení.
Nejprve dokážeme, že je druhů bloků málo, a odhadneme potřebný počet operací na předvýpočet všech možných dotazů pro všechny bloky.
Zkusme proto odhadnout celkový počet různých druhů bloků. Protože platí, že d ∈O(log log N), omezme d shora výrazem c · log log N, kde c je nějaká kladná konstanta větší než 1:
| dd | ≤ (c · log log N)c · log log N |
| = cc · log log N ·(log log N)c · log log N | |
| = (log N)c log c ·2c · log log N · log log log N. |
| 1 |
| 2 |
Celkový počet druhů bloků tedy bude ležet v O((log N)k ·√N), kde k je nějaká konstanta, a tudíž celkově v O(N).
Rozmysleme si navíc, že pokud si pro každý druh bloku předpočítáme všechny možné dotazy a předvýpočet pro jeden druh zabere polynomiální čas vzhledem k délce bloku d, zůstává celkový čas na předvýpočet v O(N).
Nyní, když víme, že umíme dostatečně rychle předpočítat výsledky všech dotazů na třetí úrovni, zbývá vyřešit, jak pro každý blok v posloupnosti nalézt odpovídající druh a jak nakonec přečíslovat předpočítanou hodnotu zpět na správnou barvu.
Nejprve každý druh bloku zakódujeme do čísla o O(log N) bitech. Pod takto vzniklými čísly budeme v tabulce uchovávat odpovědi pro příslušné druhy bloků.
Protože si můžeme každý druh bloku představit jako seznam O(log log N) čísel, z nichž každé má bitovou reprezentaci délky O(log log N), stačí tato čísla spojit do jednoho. To lze provést pomocí operací součtu a bitového posunu.
Dále každý blok v posloupnosti přečíslujeme a vytvoříme pomocné pole, které bude indexované přečíslovanými barvami a bude uchovávat jejich původní hodnoty.
Blok poté projdeme zleva doprava a zpracujeme jednotlivé pozice. Pokaždé, když se přesuneme na novou pozici, zjistíme nejprve, zda jsme její barvu již přečíslovali.
K tomu stačí nahlédnout na předchozí výskyt dané barvy (vzpomeňme si na pomocné seznamy pozic barev). Pokud se tento výskyt nachází mimo aktuální blok, narazili jsme na barvu poprvé a přiřadíme jí nejnižší dosud nepoužité číslo a aktualizujeme pole s původními hodnotami barev. Pokud se předchozí výskyt nachází uvnitř bloku, použijeme číslo barvy, na které byl přečíslován.
Na závěr přečíslovaný blok zakódujeme do čísla a tím jednoznačně určíme jeho druh.
Tím je naše práce hotová. Pokud padne dotaz do bloku na třetí úrovni, vezmeme číslo jeho druhu, najdeme v tabulce odpověď pro příslušný dotaz, a případnou barvu s nadpoloviční většinou poté jednoduše přečíslujeme zpět na její původní hodnotu.
Nalezli jsme tak nakonec řešení, které skutečně potřebuje jen O(N) času na předvýpočet a O(1) času na dotaz.
 37-2-S Lexery útočí (Zadání)
37-2-S Lexery útočí (Zadání)
Seriál lze odevzdávat za snížený počet bodů až do konce školního roku. Řešitelům, kteří už druhé sérii odevzdali, rozešleme vzorové řešení napřímo. Pokud chceš tuto sérii přeskočit a začít řešit další díl, můžeš si o vzorové řešení napsat na ksp@mff.cuni.cz.