Třetí série třicátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

Praktická opendata úloha37-3-1 Robot (Zadání)

Najdôležitejšie pri riešení tejto úlohy je uvedomiť si, aké prípady môžu nastať. Keď im budeme rozumieť, môžeme už úlohu vyriešiť pomocu jednoduchého prehľadávania grafu.

Zaujíma nás, ktoré políčka skladu sú dosiahnuteľné, teda na ktoré vieme robota prinútiť ísť. Určite to platí pre políčko, na ktorom začína. Ďalej teda musíme ísť z neho. Pokiaľ má toto políčko jedno alebo dve voľné susedné políčka, môžeme robotovi prikázať ísť na opačné pole, než chceme aby šiel, a prinútiť ho tak spraviť krok požadovaným smerom.

Pokiaľ má však susedných políčok viac, má robot po každom príkaze aspoň dve možnosti kam sa pohnúť, a teda nevieme ho dostať ani na jedno susedné políčko, pretože sa vždy pohne inak, než chceme.

Stačí nám teda spustiť BFS alebo DFS z počiatočného políčka a pokračovať len po políčkach, ktoré majú najviac dvoch susedov. Vždy keď takto nájdeme pascu, určite je dosiahnuteľná, takže všetky pasce, ktoré nájdeme, budú označené správne. Funguje takéto riešenie? Bohužiaľ nie.

Problémom je, že stále môžu existovať pasce, ktoré sme týmto procesom neoznačili. V nasledujúcom príklade môžeme vysávač naviesť do každej pasce napriek tomu, že doterajším algoritmom by sme neoznačili ani jednu:

##.P.
V..#P
##.P.

Ale v tomto podobnom príklade môžeme vysávač naviesť iba do prvej pasce v strednom riadku, nevieme ho naviesť do žiadnej zo zvyšných troch.

##.P.##
V..#P.P
##.P.##

Predošlým algoritmom by sme označili len prvé tri políčka cesty k pasciam (vrátane začiatočného). Využijeme teda tieto príklady a pridáme pozorovanie: okrem predošlých označených pascí dokážeme vysávač naviesť aj do takých, ktoré

Tieto pasce vieme nájsť tak, že z každej pasce spustíme BFS prehľadávanie, ktorým sa pokúsime dostať na štartovné políčko. Pokiaľ navštívime križovatku (čo vieme zistiť z počtu susedov daného políčka), označíme si, že na to, aby sme z nej mohli pokračovať, musíme ju navštíviť ešte raz za každú ďalšiu cestu, ktorá do nej vedie, okrem tej, ktorou chceme pokračovať (teda o dva menej, ako je počet jej susedných políčok, pretože z jedného sme práve prišli a jedným odídeme).

Vždy, keď danú križovatku navštívime znova, jej počítadlo znížime. Ak sa počítadlo križovatky dostane na nulu, pridáme ju do fronty pokračujeme z nej pri prehľadávaní. Ak narazíme na štartovné políčko, označíme pascu, z ktorej sme začali prehľadávanie, ako dosiahnuteľnú.

Toto prehľadávanie má časovú zložitosť O(R ×S ×P), kde P je počet pastí, pretože teoreticky môže byť potrebné prejsť pre každú pascu celý sklad.

Program (Python)

Úlohu připravili: Daniel Culliver, Ján „Janči“ Plachý

Praktická opendata úloha37-3-2 KSP-Nim-Vim (Zadání)

Úloha se ukázala být výrazně zákeřnější, než jsme plánovali. Proto nejprve vyřešíme její jednodušší variantu. Pak si uvědomíme, proč přímočaré zobecnění tohoto řešení na celou úlohu nefunguje. Následovat bude několik pozorování o struktuře optimální posloupnosti příkazů, ze kterých nakonec vykoukáme, jak řešení opravit.

Jednodušší úloha

Nejprve si rozmyslíme, jak by se úloha řešila s méně svérázným textovým editorem, který by vkládal a mazal samostatné znaky. Všimneme si, že takové příkazy jsou na sobě nezávislé – v optimální posloupnosti příkazů se jistě nestane, že bychom vložený znak později smazali. Díky tomu můžeme příkazy seřadit zleva doprava: dostaneme posloupnost vkládání, mazání a posunů kurzoru doprava.

Označíme α vstupní text a n jeho délku, podobně β výstupní text a m jeho délku. Dále bude α[i] značit i-tý znak řetězce α (indexováno od 0) a α[:i] prefix tvořený prvními i znaky řetězce α, tedy α[0]α[1]… α[i-1].

Definujme číslo D(i,j) jako minimální počet příkazů, kterými z α[:i] vytvoříme β[:j]. Rozebereme, čím může optimální posloupnost příkazů končit:

Z těchto tří možností si vybereme tu, která nám dá nejmenší výsledek:

D(i,j) = min(D(i-1,j)+1, D(i,j-1)+1, D(i-1,j-1)),

přičemž poslední člen se do minima zahrne jen tehdy, je-li α[i-1] = β[j-1].

To nám dává návod, jak tabulku všech D(i,j) vyplňovat po řádcích. Na okrajích bude D(0,0)=0, D(i,0)=i a D(0,j)=j. Náš vztah pro D(i,j) se odkazuje jen na hodnoty vlevo a/nebo nahoře od pozice (i,j), které už máme spočítané.

V čase O(nm) vyplníme celou tabulku. Pak nám D(n,m) řekne, jak z celé α vyrobit celou β. Zkrátka dynamické programování jak z učebnice (kapitola 12.3 v Průvodci).

Totéž bychom mohli interpretovat jako graf: Vrcholy budou uspořádané dvojice (i,j) s (0,0) v levém horním rohu. Hrany povedou o 1 doprava (mazání znaku), o 1 dolů (vložení znaku) a šikmo doprava dolů (přeskočení znaku, shoduje-li se). Cesty z (0,0) do (n,m) odpovídají hledaným posloupnostem příkazů. Ohodnotíme-li svislé a vodorovné hrany 1 a šikmé 0, stačí najít nejkratší cestu. To jde provést indukcí podle topologického pořadí, neboť graf je acyklický. Průchod po řádcích dá toplologické pořadí. Výsledný algoritmus bude takřka identický s předchozím dynamickým programováním.

Nečekaný zádrhel

Nabízí se podobným způsobem vyřešit zadanou úlohu, v níž máme příkazy na vložení nebo smazání dvojice nebo trojice znaků a opět zdarma pohyby kurzorem. Tyto příkazy můžeme zase popsat vztahy typu D(i,j) = D(i,j-2) + 1 pro vložení dvojice znaků, D(i,j) = D(i-3,j) + 1 pro smazání trojice atd.

Co když potřebujeme vložit jediný znak znak x? To můžeme nahradit vložením xyz a následným smazáním yz. To vede na vztah D(i,j) = D(i,j-1) + 2.

Tím se nám ovšem rozbil předpoklad, že příkazy jsou nezávislé. Ve skutečnosti se mohou překrývat docela komplikovaně (jedno mazání může ležet přes 2 různá vložení, mezi nimiž se mohou vyskytovat původní znaky řetězce α). Proto už vůbec není jasné, co znamená seřadit příkazy zleva doprava, a celá myšlenka řešení se rozpadne.

Struktura optimálních řešení

I v této temné chvíli naštěstí mihotá světélko naděje. Ukážeme, že v optimálních řešeních většina překryvů nenastane, nebo se jim alespoň dá vyhnout.

Budeme uvažovat nějakou optimální posloupnost příkazů a postupně ji budeme upravovat, aby měla čím dál jednodušší strukturu, a přitom se neprodloužila. Pohyby kurzorem zanedbáme, protože se za ně neplatí, a u příkazů vkládání a mazání si budeme pamatovat, na které pozici v řetězci nastanou.

Označíme I příkaz pro vkládání (insert), D příkaz pro mazání (delete). Ik a Dk znamená verzi pro vložení/smazání k znaků.

Předchází/následuje bude popisovat vztahy v čase (pozice v posloupnosti příkazů), nalevo/napravo/překrývá se vztahy v prostoru (pozice v editovaném řetězci).

Krok 1: Všechny inserty lze provést před všemi delety.

Mějme posloupnost příkazů, pro kterou tvrzení neplatí. Nachází se tam tedy inverze: delete D, po kterém bezprostředně následuje insert I.

Představme si, co se stane, když I a D v nějaké inverzi prohodíme. I zjevně proběhne bud nalevo nebo napravo od D, takže I neovlivní, jak D proběhne, kromě toho, že může posunout indexy. Ty ale můžeme snadno opravit.

Pokud se tímto způsobem budeme zbavovat první inverze v pořadí příkazů, bude se postupně pozice nejlevější inverze posouvat ke konci posloupnosti, až budou všechny inserty před všemi delety. Počet operací tím nezměníme, takže posloupnost bude nadále optimální.

Krok 2: Dva příkazy téhož druhu se nepřekrývají.

Dva delety se překrývat nemohou.

Pokud se překrývaly dva inserty, znamená to, že nejprve vložíme jeden řetězec a pak dovnitř něj druhý. Tím vznikne podřetězec z 4–6 znaků, který ale umíme vyrobit i dvěma po na sebe navazujícími inserty.

Krok 3: Delete se překrývá s nejvýše 1 insertem.

Delete se může překrývat s nejvýše 2 inserty. Mezi těmito inserty mohou být nějaké znaky původní posloupnosti. Uvažme nejlevější takový delete.

Pokud mezi inserty nejsou žádné původní znaky, nejprve dva inserty vytvoří 4–6 znaků, pak z nich delete smaže 2–3, takže zbude 1–4 znaků. Každý řetězec této délky ovšem umíme vyrobit jednodušeji: délku 2–3 pomocí I2 nebo I3, délku 4 dvěma I2, délku 1 pomocí I3, jehož zbytek smaže D2. Tím dostaneme kratší posloupnost příkazů se stejným výsledkem, takže takže v optimální posloupnosti tento případ nemohl nastat.

Pokud mezi inserty leží nějaký původní znak, musí být jediný a delete musí být D3 (jinak by delete nemohl zasáhnout do dvou insertů současně), tím pádem delete z každého insertu smaže jeden znak. Uvažujme možné kombinace délek insertů.

V rozborech případů budeme dodržovat následující konvence: Velká písmena pochází z původního řetězce α, malá písmena z nějakého předchozího insertu, tučná písmena maže delete. Svislé čárky oddělují jednotlivé inserty jak od sebe navzájem, tak od původních znaků.

Možné kombinace tedy jsou:

Pokaždé tedy umíme dvojitý překryv nahradit jednoduchým, aniž by příkazů přibylo. Žádný nový dvojitý překryv nevznikne, takže po konečně mnoha opakováních se všech násobných překryvů zbavíme.

Blížíme se do finále

Kombinací předchozích tří kroků získáme, že aspoň jedna z optimálních posloupnosti splňuje to, že se skládá z nepřekrývajících se částí těchto typů:

Tyto části opět můžeme seřadit zleva doprava a získat rekurentní vzorec. (Pořadí z kroku 1 už dodržujeme jen v rámci části.)

Jen je ještě potřeba dořešit, jak mohou vypadat dvojice insertu s deletem (přičemž delete může mazat i znaky původního textu). Budeme se držet značení z důkazu předchozího kroku:

Dvojice, které neprovedou nic nebo jsou ekvivalentní s D2, nemusíme brát v úvahu – téhož efektu jde dosáhnout méně příkazy. Variantu I2D2 umíme provést i bez překryvu. Ostatní dvojice nám dvěma příkazy dokáží simulovat I1, D1, I1D1, I2D1, I1D2 (nepřekrývající se).

Hotový algoritmus

Teď už můžeme dát dohromady celý algoritmus. Z předchozího rozboru případů odvodíme:

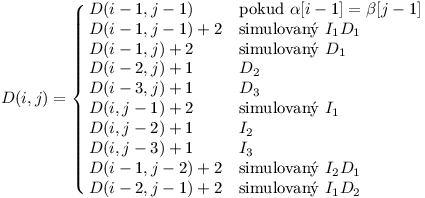
Varianty, kterým vyjdou indexy mimo tabulku, vynecháme.

Tabulku můžeme opět vyplnit po řádcích v čase O(nm), jako okrajovou podmínku postačí položit D(0,0)=0.

Ještě je potřeba domyslet, jak rekonstruovat posloupnost příkazů. Na to stačí pamatovat si při výpočtu tabulky, pro kterou variantu se minimum nabývalo. To umožní rekonstruovat posloupnost pozpátku od D(n,m).

Program (Python)

Úlohu připravili: Honza Černohorský, Martin „Medvěd“ Mareš, Vladimír Sklenár, Dan Skýpala

Teoretická úloha37-3-3 Hledání podmatice (Zadání)

Kdybychom tuto úlohu řešili v 1D světě, šlo by o klasický problém hledání v textu. Na ten existuje například algoritmus KMP, o kterém se dočtete v kuchařce. My ale potřebujeme hledat ve 2D. Celkem přímočarý způsob, jak převést algoritmus do více dimenzí, je zpracovávat jednotlivé osy postupně.

Nejdříve budeme hledat po řádcích. Jelikož hledáme výskyty několika různých řádků malé matice, použijeme algoritmus Aho-Corasicková. Ten má navíc tu výhodu, že pokud jsou některé řádky malé matice identické, tak je najdeme, protože jim bude odpovídat stejný vrchol v trii. Projdeme každý řádek velké matice a na všech políčkách si zaznamenáme, v jakém stavu (vrcholu trie) jsme byli. Tím dostaneme novou matici, která nám říká, jestli a jaký malý řádek na daném místě končí.

Poté budeme hledat po sloupcích. Sloupec obsahuje pravý kraj výskytu malé matice, právě když jsou v něm ve správném pořadí konce řádků malé matice. To je opět hledání v textu, jen s jinou abecedou tvořenou vrcholy trie. Jelikož je tentokrát jenom jedna jehla, použijeme algoritmus KMP. Projdeme každý sloupec zpracované velké matice. Každý výskyt jehly pak odpovídá pravému dolnímu rohu výskytu malé matice.

Celková časová složitost algoritmu je O(N2 + K2). Trii si připravíme v O(K2), KMP tabulku v O(K) a obě prohledávání trvají O(N2). Pohyb v trii sice závisí na abecedě, ale ta je v prvním prohledávání konstantní. Ve druhém hledání máme abecedu velikosti až K2, ale KMP naštěstí umí pracovat bez zpomalení s libovolně velkou abecedou. V druhém prohledávaní můžeme vynechat prvních K - 1 sloupců, protože nemůžou obsahovat konec malého řádku, ale asymptoticky to nic nezmění.

Program (C++)

Program (Python)

Úlohu připravili: Jan Adámek, Ján „Janči“ Plachý

Praktická opendata úloha37-3-4 Výhybky (Zadání)

(Ne)obvyklé hradlo

Nejdřív si ukažme, že z výhybkového hradla jdou sestrojit hradla, která všichni známe. NOT sestrojíme jednoduše – vybereme nulu, pokud je vstupní hodnota jedna, a opačně:

NOT: X 0 1

U ANDu si všimneme, že pokud první vstup je nula, výsledek je určitě nula. Jinak stačí vrátit druhý vstup:

AND: X Y 0

OR vyřešíme obdobně:

OR: X 1 Y

Zbývá vyřešit XOR. Pokud oba vstupy jsou jedna, vrátíme nula. Jinak vrátíme jejich OR:

AND: X Y 0
OR: X 1 Y
XOR: AND 0 OR

Čas řešit

Nyní pojďme řešit jednotlivé podúlohy. V první podúloze stačí udělat AND všech vstupů. Abychom dosáhli logaritmické hloubky, tak stačí udělat ANDy dvou sousedních hodnot. (Pokud je počet vstupů lichý, tak nám jedna zbude.) A to stačí dělat opakovaně, čímž skončíme s jednou hodnotou. Protože v každé vrstvě vydělíme počet hodnot dvěma (a zaokrouhlíme nahoru), hloubka bude logaritmická.

Druhou podúlohu vyřešíme obdobně – stačí vyměnit AND za OR.

V třetí podúloze chceme zjistit, jestli máme právě jednu jedničku. Na to zobecněme náš postup. Máme nějaké hodnoty reprezentující úseky. (V předchozích podúlohách to byl AND nebo OR daného úseku.) Poté v jedné vrstvě zkombinujme sousední dvojice do jedné, čímž dané hodnoty budou odpovídat úseku o dvojnásobné délky. (Až na případy, kdy počet hodnot je lichý.)

A v této podúloze si budeme posílat následující dvojici:

Na začátku v každém úseku o máme dvojici (i-tý vstup, konstantní nula). Kombinovat dvojice s již zkonstruovanými hradly zvládneme následovně: 
one = one1 OR one2
more = (one1 AND one2) OR more1 OR more2

Na konci stačí pouze zkontrolovat, že výsledná dvojice je (1, 0). To můžeme udělat následovně: Ze všech hodnot, co mají být 0, uděláme NOT, a následovně všechny hodnoty zANDujeme.

Vzhůru na čtvrtou úlohu – zde je už doopravdy zapotřebí počítat počty jedniček. Naše úseky budou reprezentovány log n bity, udávajícími počet jedniček v daném úseku. (Na začátku jen vstupní hodnoty zleva doplníme konstantními nulami.) A zkombinovaní dvou úseku odpovídání sečtení dvou log n bitových čísel.

Na to si nejdříve sestrojme primitivní obvod, který sečte tři bity – bit z levého úseku, bit z pravého úseku a bit za přenos. Výsledek bude tedy dvoubitové číslo (carry, result):

Když už máme sčítačku, tak jsme je schopni zapojit za sebe pro libovolně dlouhá čísla (příklad pro 4 bity):

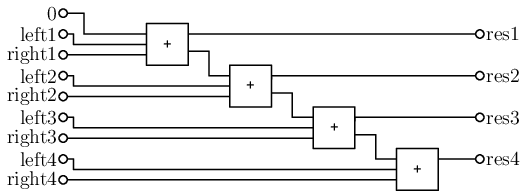
Kde poslední carry bit prostě zahodíme – víme, že tolik jedniček v našem vstupu prostě nemůže být. Na závěr stačí opět znegovat bity, co mají být nulové, a udělat AND.

Nicméně tohle použije moc hradel. Uděláme proto ještě jednu optimalizaci – všimneme si, že v i-té vrstvě jedničkových může být pouze nejnižších i bitů. Když tyto nepotřebné části obvodu odstraníme, už se do limitu počtu hradel vlezeme.

Program (Python)

Magnum opus

Na závěr zmiňme, že řešení čtvrté podúlohy jde použít na řešení všech ostatních. – Stačí spočítat počet jedniček a porovnat ho s požadovaným počtem. Pouze u podúlohy na alespoň jednu jedničku stačí porovnat s nulou a udělat negaci.

Program (Python)

Úlohu připravili: Dan Skýpala, Ben Swart

Teoretická úloha37-2-X1 Intervalové většiny (Zadání)

Moc se omlouváme, ale řešení intervalových většin nám také ještě chvilku zabere sepsat.

Teoretická úloha37-3-S Parsery vrací úder (Zadání)

Seriál lze odevzdávat za snížený počet bodů až do konce školního roku. Řešitelům, kteří už třetí sérii odevzdali, rozešleme vzorové řešení napřímo. Pokud chceš tuto sérii přeskočit a začít řešit další díl, můžeš si o vzorové řešení napsat na ksp@mff.cuni.cz.