Čtvrtá série třicátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 37-4-1: Otočení vlaku
- 37-4-2: Bomby a tunel
- 37-4-3: Detekce (3/4)-cyklů
- 37-4-4: Asteracer
- 37-4-S: Proměnné se probouzí
- 37-4-X1: Mehrdeutige Wortbildung
 37-4-1 Otočení vlaku (Zadání)
37-4-1 Otočení vlaku (Zadání)
Přeložme úlohu do grafové terminologie. Železniční uzly jsou vrcholy, tratě jsou neorientované hrany.
Dle zadání hledáme nejkratší posloupnost vrcholů, která začíná a končí v D, kde se dle drážních předpisů mohou vrcholy opakovat – tedy uzavřený sled. Avšak nesmíme nikde provést úvrať, tedy ve sledu nesmí existovat posloupnost u, v, u.
Navíc chceme, aby na konci byla souprava otočená. To však bude pro každý uzavřený sled vždy platit: Zakázání úvratí zaručuje, že předek soupravy vždy jede po směru hrany. Jelikož D má stupeň 1, musí souprava použít stejnou hranu pro cestu tam i zpět – při cestě zpět je zadní část soupravy otočená ven z depa a souprava je otočená.
Představme si, že máme nejkratší sled, co prochází hranou e = (u, v). Tento sled pak můžeme popsat jako slepení dvou sledů D, …, u a v, …, D hranou e. Zkusme tyto dva sledy nahradit nejkratšími cestami z D do u a v. Délka takto vzniklého sledu bude bude Le = d(u) + ℓ(e) + d(v), kde ℓ(e) je délka hrany e a d(x) je délka nejkratší cesty z D do vrcholu x.
Protože délka sledu je pro graf s nezápornými délkami hran zdola omezená délkou cesty, tento nově vzniklý sled nebude delší. Tady ale narazíme na problém: pokud e je součástí nejkratší cesty do u, takové slepení vytvoří posloupnost v, u, v, což je úvrať. Obdobně, pokud by e byla na nejkratší cestě do v, dostaneme úvrať u, v, u. Musíme proto zařídit, aby e nebyla na ani jedné nejkratší cestě.
Uvažme strom nejkratších cest z vrcholu D – podstrom původního grafu, kde pro každý vrchol v jediná cesta z D do v odpovídá nejkratší cestě v původním grafu. Jelikož jde o podstrom původního grafu, pro každý cyklus v grafu alespoň jedna jeho hrana nebude součástí tohoto stromu. Tyto hrany označme za nestromové.
Dále ukážeme, že v každém bezúvraťovém uzavřeném sledu bude cyklus: vrchol D se určitě opakuje, tudíž existuje podposloupnost vi ≠ vi+1 ≠ vi+2 ≠ …≠ vi+k = vi. Protože kvůli zákazu úvratí vi ≠ vi+2, musí být k ≥ 3 a tyto vrcholy tvoří cyklus.
Tudíž v každém korektním sledu musí existovat nestromová hrana e = (u, v). Ta splňuje hledanou vlastnost, tudíž můžeme aplikovat rozdělení sledu a nahrazení částí nejkratšími cestami. Tím dostaneme alespoň stejně dobré nové řešení.
Jako výsledek dostáváme, že hledaná nejkratší trasa je sled, který se skládá z nejkratší cesty z D do u, hrany e a nejkratší cesty z v do D, pro kterou je Le nejmenší přes všechny nestromové hrany. Náš algoritmus proto najde strom nejkratších cest, pak spočítá délky takto vytvořených sledů pro každou nestromovou hranu a z nich vrátí minimum.
Strom nejkratších cest včetně vzdáleností vrcholů od D umíme najít Dijkstrovým algoritmem. Délku sledu daným nestromovou hranou e umíme spočítat v konstantním čase, proto tato část algoritmu potrvá čas O(M). Rekonstrukce nejkratší trasy nakonec potrvá O(K) ⊆ O(N).
Celková časová složitost našeho algoritmu tedy odpovídá časové složitosti Dijkstrova algoritmu. Ten má s vhodně zvolenou haldou (například Fibonacciho) časovou složitost O(N log N + M).
 37-4-2 Bomby a tunel (Zadání)
37-4-2 Bomby a tunel (Zadání)
Jednodušší varianta
Slíbili jsme, že v několika prvních vstupech je k vyhloubení tunelu nutné použít všechny bomby. Je tedy třeba pouze rozhodnout o pořadí, v jakém je budeme odpalovat.
O každé bombě víme, že vyhloubí určitý počet metrů a má nějakou váhu. Intuitivně tedy dává smysl, že bombu, která je velmi těžká a vyhloubí krátký úsek tunelu, bychom měli odpálit dříve než lehkou bombu, která vyhloubí dlouhý úsek.
Zkusme tuto myšlenku formalizovat. Zavedeme si tzv. efektivitu. Ta bude pro bombu s váhou wi a schopností vyhloubit délku tunelu di rovna podílu di / wi.
Platí pak, že získáme pořadí bomb tak, že je libovolným algoritmem setřídíme vzestupně podle efektivity, tedy od bomby s nejmenší efektivitou po tu nejefektivnější.
Pojďme si toto tvrzení dokázat.

Nejprve ukážeme, že je optimální pořadí určitě vzestupně setřízené.
Představme si, že máme nějaké optimální pořadí odpalů, a podívejme se v něm na libovolné dvě sousední bomby.
Nechť má první bomba váhu w1 a délku d1, a druhá bomba váhu w2 a délku d2. Protože je dané pořadí optimální, musí platit, že prohození těchto dvou bomb nezlepší celkovou spotřebu energie. To lze vyjádřit následující nerovností:
V této nerovnosti značí E spotřebovanou energii na ostatní bomby (kterou prohození našich dvou bomb neovlivní) a d je délka tunelu vyhloubená před použitím těchto dvou bomb.
Upravme nerovnost:
| w2 ·(d1 + d) + w1 ·d | ≤ w1 ·(d2 + d) + w2 ·d | ||||
| w2 ·d1 | ≤ w1 ·d2 | ||||
| ≤
|
Tím jsme dokázali, že efektivita první bomby je menší nebo rovna efektivitě druhé. Z toho plyne, že jsou bomby v optimálním řešení setřízené vzestupně.
Setřízených posloupností může být nicméně více (máme-li více bomb se stejnou efektivitou), pojďme ukázat, že vyhovuje každá.
K tomu si stačí rozmyslet, že pokud dvě sousední bomby se stejnou efektivitou prohodíme, spotřebované množství energie zůstane stejné.
Dokázat to lze tak, že předchozí nerovnosti změníme na rovnosti a projdeme je v opačném pořadí.
K vyřešení úlohy tedy stačí bomby setřídit v O(B log B) podle jejich efektivity.
Dodejme, že by v případě velkých vah a vyražených délek bomb mohlo dojít k zaokrouhlovacím chybám. Můžeme jednotlivé efektivity bomb porovnávat jako zlomky a vždy je před porovnáním převést na společný jmenovatel, čímž se tomuto problému vyhneme.
Obecný případ
Z pozorování výše známe pořadí, v jakém se vyplatí bomby odpálit. Bohužel však tentokrát nevíme, které konkrétní bomby použít.
Ukážeme, že k nalezení optimální podmnožiny bomb lze použít postup podobný klasickému řešení problému batohu. Naše řešení navíc nenalezne optimální výběr pouze pro délku M, ale pro všechny délky v intervalu od 0 do M.
Aby bylo zřejmé, že náš algoritmus skutečně funguje, začneme velmi pomalým řešením hrubou silou a budeme jej postupně upravovat, dokud nedosáhneme požadované efektivity.
Řešení hrubou silou
Určitě validní řešení by spočívalo ve vyzkoušení všech 2B podmnožin bomb.
Protože pro každou podmnožinu jednoznačně známe pořadí, v jakém se vyplatí bomby odpalovat, můžeme pro každou z nich spočítat, kolik energie celkový odpal spotřebuje. Známe také délku tunelu, kterou taková množina bomb dohromady vyhloubí.
Můžeme tedy v průběhu generování podmnožin v poli indexovaném délkou udržovat aktuálně nejmenší známé množství energie potřebné k vyhloubení každé možné délky menší nebo rovné M, spolu s informací o bombách, které jsme k tomu použili.
Na konci algoritmu toto pole bude obsahovat pro každou délku minimální množství energie a odpovídající množinu bomb.

Systematické zkoušení podmnožin
Stále budeme zkoušet všechny podmnožiny, takže výsledek pro každou délku zůstane stejný, avšak podmnožiny tentokrát vygenerujeme v konkrétním pořadí.
Na počátku setřídíme bomby vzestupně podle jejich efektivity a budeme je procházet od nejméně efektivní po nejvíce efektivní.
Při zpracování každé bomby vygenerujeme všechny podmnožiny, jejichž nejefektivnější bomba je právě ta aktuální, a tyto podmnožiny zpracujeme stejným způsobem jako dříve.
Navíc pro každou bombu budeme generovat podmnožiny v pořadí podle délek, a to vzestupně: nejprve ty, jejichž délky se sečtou na 0, poté 1, 2, … , až po M.
Zrychlujeme
Představme si, že generujeme všechny podmnožiny, jejichž nejefektivnější bomba má délku d a součet délek bomb v podmnožině je S.
Protože má v dané fázi nejefektivnější bomba délku d, mají všechny zkoušené podmnožiny bez této bomby součet délek roven S - d. Můžeme proto algoritmus urychlit tak, že ze všech dosud vygenerovaných podmnožin, jejichž bomby mají součet délek roven S - d a jejichž nejefektivnější bomba je méně efektivní než ta aktuální, rovnou vybereme tu, která vyžaduje nejmenší množství energie.
Protože aktuální bombu přidáváme až na konec odpalovací sekvence, lze výsledné množství energie spočítat v konstantním čase – s využitím informace o minimální energii potřebné pro délku S - d bez aktuální bomby.
Pokud je takto získaná nová podmnožina horší než nějaká již známá, která se přesně sečte na S, jednoduše ji zahodíme, protože už známe lepší řešení.
Tím jsme získali kostru vzorového řešení. Nyní zbývá jen popsat konkrétní implementaci s efektivní rekonstrukcí použitých bomb.

Výsledný algoritmus
Na počátku setřídíme bomby podle jejich efektivity.
Dále si připravíme dvourozměrné pomocné pole o rozměrech (B+1)×(M+1), které bude na řádku i a ve sloupci j uchovávat nejmenší množství energie, s jakým jsme schopni vyhloubit úsek délky j, pokud k tomu můžeme použít pouze některé z prvních i nejméně efektivních bomb. Ve stejném políčku budeme také uchovávat číslo nejefektivnější použité bomby, která dané řešení umožnila.
Následně začneme procházet bomby od nejméně efektivní po nejvíce a postupně vyplňujeme pomocné pole po řádcích.
Při vyplňování i-tého řádku pro každou délku tunelu j od 0 do M vyzkoušíme dvě možnosti:
- bombu číslo i nevyužijeme – v tomto případě jednoduše zkopírujeme hodnotu energie a poslední použitou bombu z předchozího řádku (i - 1) ve stejném sloupci (j).
- bombu číslo i využijeme – pokud délka aktuální bomby di není větší než j, zjistíme energii potřebnou k vyhloubení délky j - di na předchozím řádku (tedy bez použití aktuální bomby), přičteme k ní energii spotřebovanou bombou číslo i (vypočtenou jako wi ·(j - di)), a tuto hodnotu porovnáme s energií v případě, že bombu nevyužijeme. Pokud je tato hodnota menší, aktualizujeme hodnotu energie v poli a uložíme informaci, že bomba číslo i byla použita.
Pokud řešení existuje, tak bude mít po dokončení tohoto postupu pomocné pole v políčku [B][M] uloženo nejmenší množství energie nutné k vyhloubení tunelu délky M a poslední použitou bombu.
Zbývá provést rekonstrukci použitých bomb. Začneme v políčku [B][M]. Pokud je políčko prázdné, znamená to, že tunel nelze vyhloubit žádnou kombinací bomb.
Jinak zahájíme zpětnou rekonstrukci bomb v opačném pořadí.
Pokud je v aktuálním políčku uvedeno, že byla použita bomba číslo i, přidáme tuto bombu do seznamu použitých bomb a posuneme se do políčka na řádku i - 1 a ve sloupci odpovídajícím zbývající délce tunelu (j - di).
Tento postup opakujeme, dokud nevyčerpáme zbývající délku tunelu. Výsledkem je seznam bomb použitých k dosažení optimálního řešení, který je potřeba na závěr otočit.
Časová složitost tohoto algoritmu je O(B log B + BM) a paměťová O(BM).
 37-4-3 Detekce (3/4)-cyklů (Zadání)
37-4-3 Detekce (3/4)-cyklů (Zadání)
Nejprve popíšeme, jak nalézt 4-cyklus, a následně tento postup zobecníme na nalezení 3-cyklu či 4-cyklu.
Nalezení 4-cyklu
Podívejme se, jaké vlastnosti má takový 4-cyklus.
Pojmenujme jeho vrcholy a, b, c, d podle toho, jak bychom je navštívili, pokud bychom šli po jeho obvodu. Všimněme si, že vrcholy a a c spolu sdílí dva sousedy b a d.
Zároveň platí, že kdykoliv máme dva vrcholy x a y, které spolu sdílí dva sousedy, můžeme vyrazit z vrcholu x, vstoupit do jednoho souseda, z něj vstoupit do y a nakonec se vrátit přes druhého souseda zpátky do x. Tyto vrcholy tedy tvoří 4-cyklus.
Nalezení 4-cyklu je tedy ekvivalentní s nalezením dvou vrcholů, které sdílí dva sousedy.
Proto pro každý vrchol postupně vygenerujeme všechny dvojice jeho sousedů a jakmile vygenerujeme nějakou dvojici podruhé, nalezli jsme 4-cyklus.
Všimněme si, že takto vygenerujeme nejvýše O(N2) dvojic. Kdyby totiž vygenerovaných dvojic bylo více, museli bychom nějakou z nich nutně vygenerovat dvakrát a zastavili bychom se dříve.
Počet vygenerovaných dvojic je lineární s velikostí vstupu. Abychom nicméně skutečně dosáhli časové složitosti O(N2), je třeba vyřešit, jak rychle vygenerovat všechny dvojice a jak po vygenerování každé dvojice sousedů rychle ověřit, zda již nebyla někdy v minulosti vygenerována a kým.
K rychlému generování dvojic si na začátku převedeme reprezentaci grafu v O(N2) na seznam sousedů pro každý vrchol. V něm už poté snadno pro každý vrchol vygenerujeme pomocí dvou zanořených cyklů všechny dvojice jeho sousedů.
K ověření vygenerování dvojic nám pro změnu pomůže další matice o rozměrech N ×N. Na počátku bude obsahovat samé -1 a jakmile vygenerujeme dvojici vrcholů i, j, zapíšeme na pozice Aij a Aji číslo vrcholu, pomocí kterého jsme tuto dvojici vygenerovali.
Jakmile se pokusíme do matice zapsat nějakou dvojici podruhé, nalezli jsme 4-cyklus a umíme ho rovnou rekonstruovat.
Získali jsme tak algoritmus mající časovou i paměťovou složitost O(N2).
Nalezení 3-cyklu či 4-cyklu
Pojďme se nejprve inspirovat postupem pro nalezení 4-cyklu a nějak podobně nalézt i 3-cyklus.
K tomu si rozmysleme, že je nalezení 3-cyklu ekvivalentní s hledáním vrcholu, jehož nějaká dvojice sousedů je spojená hranou.
Zkusme tedy stejným způsobem generovat všechny dvojice sousedů každého vrcholu a pokaždé se podívat do původní matice sousednosti, zda mezi vygenerovanou dvojicí leží hrana.
Tento postup bude určitě fungovat, nicméně bychom tentokrát mohli mít smůlu a vygenerovat až O(N3) dvojic. Jako příklad uvažme úplný bipartitní graf KN/2, N/2, kde má každý z O(N) vrcholů stupeň O(N), ale 3-cyklus se v něm určitě nenachází.
Zde nám nicméně pomůže předchozí pozorování: jakmile bychom vygenerovali víc než O(N2) dvojic, museli bychom nějakou dvojici nutně vygenerovat dvakrát, a tedy v grafu nalézt 4-cyklus.
Můžeme proto nejprve zkusit detekovat 4-cyklus, a pokud žádný nenalezneme, máme jistotu, že vzniklo jen O(N2) dvojic, a můžeme spustit algoritmus na detekci 3-cyklu. Alternativně můžeme provádět obojí paralelně, tedy postupně generovat pro každý vrchol dvojice jeho sousedů a pokaždé se nejprve podívat, zda je dvojice spojena hranou, a pokud nikoliv, tak zkontrolovat, zda jsme tuto dvojici již nevygenerovali a uložit ji.
Protože vygenerujeme až O(N2) dvojic a na každou potřebujeme jen O(1) operací, bude mít výsledný algoritmus časovou i paměťovou složitost O(N2).
Detekce samotného 3-cyklu
 Ukázalo se, že umíme v O(N2) zjistit,
zda se v grafu nachází 4-cyklus,
nebo zda se v grafu nachází 3-cyklus či 4-cyklus.
Nedalo by se ale nějak rychle určit, zda graf obsahuje 3-cyklus?
Vždyť samotné zadání úlohy vybízí k tomu řešit detekci 3-cyklu a 4-cyklu jako dva oddělené problémy.
Ukázalo se, že umíme v O(N2) zjistit,
zda se v grafu nachází 4-cyklus,
nebo zda se v grafu nachází 3-cyklus či 4-cyklus.
Nedalo by se ale nějak rychle určit, zda graf obsahuje 3-cyklus?
Vždyť samotné zadání úlohy vybízí k tomu řešit detekci 3-cyklu a 4-cyklu jako dva oddělené problémy.
Bohužel se ukazuje, že je problém detekce 3-cyklu v zadaném grafu mnohem složitější než detekce 4-cyklu nebo 3,4-cyklu. Ukážeme si (bez důkazu) algoritmus s násobením matic.
Mějme zadanou matici sousednosti grafu. Platí, že se po umocnění matice sousednosti na druhou bude na i-tém řádku a j-tém sloupci nacházet počet všech sledů délky 2 mezi vrcholy i a j.
Stačí již poté jen projít všechny hrany grafu a pro každou se podívat, zda se v grafu nenachází sled délky 2, který by spojoval její konce. Tím získáme algoritmus stejně rychlý, jako je použitý algoritmus na násobení matic.
Klasický algoritmus na násobení dvou matic udělá O(N3) operací. V Průvodci labyrintem algoritmů si například můžete přečíst o Strassenově algoritmu využívajícím metodu rozděl a panuj. Ten má časovou složitost O(N2.807).
Jsou však známy ještě rychlejší algoritmy. V době vydání tohoto řešení má nejrychlejší známý algoritmus časovou složitost O(N2.371339). Má však příliš velké konstanty na to, aby byl použitelný v praxi.
 37-4-4 Asteracer (Zadání)
37-4-4 Asteracer (Zadání)
Asteracer byl z velké části inspirovaný závodní hrou Trackmania, ve které se hráči snaží co nejrychleji projet autem všechny góly a skončit v předem daném cíli. Žebříčky nejlepších časů na Trackmania mapách jsou rozděleny na dvě kategorie: běžná, ve které se počítají časy dosaženy hráči běžným hraním hry, a asistované, ve kterých je povolené vše, včetně poloautomatických a plně automatických řešičů.
Cílem návrhu systému létání a map Asteraceru bylo to, aby kratší mapy (test a sprint) byly lépe řešitelné poloautomatickými řešiči (tj. létání s pauzami/vraceními) a (marathon) byla lépe řešitelná automatickým řešením. Zvláště u marathonu jsme si říkali, že se nikomu nebude chtít létat přes všech 50 cílů, takže bude potřeba úlohu řešit automaticky…
…v praxi se ukázalo, že skoro všechna řešení, včetně všech pódiových, byla poloautomatická, a že pro vynucení automatického řešení bychom museli přidat ještě více cílů. Níže popisujeme dvě autorská řešení – jedno poloautomatické a jedno automatické.
Navíc si níže můžete prohlédnout všechna řešení do nejmenších detailů. Vizualizaci si můžete zobrazit také ve větším okně zde.
Poloautomatické (Jakub Pelc)
Asteracer jsem řešil ručním ovládáním lodi, které se ukázalo být poměrně efektivní. Na první mapě test bylo potřeba najít optimální pořadí cílů a to několikrát vyzkoušet proletět. Druhá mapa sprint byla poměrně přímočará, jen jsem experimentoval s „glitchováním“ skrz asteroidy, které jednoduchý kolizní systém umožňuje, ale nakonec nevedlo k žádným časovým úsporám. U třetí mapy marathon jsem si prostě zkusil rozmyslet nějakou rozumnou cestu všemi cíli a tu proletěl a získal tím řešení okolo 15 tisíc instrukcí, na druhý pokus s jinou cestou se mi podařilo současných 12803.
Při psaní programu jsem měl výhodu, že jsem implementoval webovou vizualizaci, tudíž mi stačilo si ji pro své účely modifikovat. Instrukce jsem zadával relativní pozicí myši vůči lodi. Program umožňoval načítat a ukládat instrukce, měl funkci „undo“, uměl přidat 10 stejných instrukcí naráz (velmi užitečné pro velké mapy) a také pro současnou pozici myši (příští instrukci) zobrazoval realtime preview jak by se loď chovala, kdyby se daná instrukce zopakovala po následujících 200 kroků, včetně zvýraznění kolizí červeně.
Automatické (Tomáš Sláma)
Automatické řešení Asteraceru je založeno na prohledávání do hloubky. Po nalezení nejkratší cesty v grafu, který jsme pro vás pro jednodušší řešení úlohy předpočítali, opakovaně hledá instrukci, jejíž opakování dostane loď co nejblíž k dalšímu vrcholu v cestě. Jelikož byly grafy předpočítány tak, aby pohyb lodi po hranách nenarážel do asteroidů, tak se vlastně jedná o intuitivní způsob jak přinutit loď, aby proletěla danou trasou bez nárazů.
Je si ovšem potřeba dát pozor na několik věcí, bez kterých řešení nefunguje.
V určitých situacích se může stát, že instrukce, které minimalizují vzdálenost lodi od dalšího vrcholu, vyústí v náraz, ať už jsou další instrukce libovolné. V takovém případě by se řešič zasekl v nekonečné smyčce. Řešením v takových situacích je zvýšit počet kroků, o které se řešič vrátí, a (o malou čast) randomizovat instrukci, aby loď nenarazila.
Pokud má mapa pouze jeden cíl, tak stačí použít Dijkstru či A* a získáme nejkratší cestu.
Pro více cílů je situace komplikovanější – v takovém případě chceme najít cestu, která navštíví všech m cílů a jeden z jejich konců je předem daný (start).
Mé řešení tento problém redukuje na m problémů obchodního cestujícího, na který má Pythoní balíček nxgraph dobré řešiče (případně lze cyklus najít hladově).
Základní princip redukce je ten, že vyzkoušíme každý možný koncový vrchol v přidáním nového „hack“ vrcholu H, nastavíme vzdálenost v-H na 0, vzdálenosti do ostatních vrcholů H-start na 0 a ostatní vzdálenosti hran do/z H na nekonečno, což vynutí přidání sekvence v-H-start do řešení a po odstranění vrcholu H získáme cestu splňující naše požadavky.
Zdrojový kód a nejlepší automatické řešení jsou k dispozici v Asteracer repozitáři.
 37-4-X1 Mehrdeutige Wortbildung (Zadání)
37-4-X1 Mehrdeutige Wortbildung (Zadání)
Máme za úkol napsat řetězec znaků, který je možný rozložit na německá slova dvěma způsoby. Tento pohled na zadání nám ale moc nepomůže – není až tak jednoduché určit, kolika způsoby je daný řetězec možné rozdělit na slova, a navíc se tento počet po přidání znaku může prudce změnit. Lepší pohled na zadání je to, že se snažíme napsat dvě posloupnosti slov, které po odstranění mezer dají stejný řetězec písmen. Budeme je ale stále psát písmeno po písmeni.
Dejme tomu, že jsme například napsali dvakrát řetězec ei.
Ei je skutečné Německé slovo, takže můžeme v jednom z řetězců slovo ukončit.
Poté můžeme k oběma řetězcům připsat s.
Eis je také slovo, takže můžeme ukončit slovo v druhém řetězci.
Tím dostaneme řetězce ei·s
a eis·.
Pokud budeme pokračovat, můžeme se dostat až ke dvojici řetězců
ei·sturm
a eis·turm.
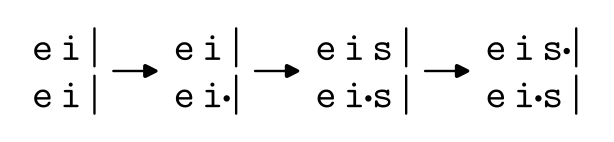
Úlohu vyřešíme prohledáváním stavového prostoru. Stavem ale nebude dvojice nedopsaných posloupností slov, těch by bylo moc. Naštěstí nás ale nemusí zajímat všechna slova, co jsme napsali – důležitá je jen dvojice slov, co jsou rozepsaná. Stavem tedy bude dvojice prefixů slov. Ze stavu můžeme přejít do jiného buď tak, že k oběma prefixům přidáme další písmeno, pokud tím vzniknou další dva prefixy slov ze slovníku, nebo tak, že jedno nebo obě slova ukončíme a nahradíme je prázdným řetězcem.

Začátek prohledávání bude pochopitelně dvojice prázdných řetězců. Nabízí se, aby tento stav byl také cílem. To bychom ale okamžitě skončili a nic nenapsali. Zastavíme se tedy o stav dříve, tedy ve stavu, ve kterém jsou oba prefixy skutečná slova, a mohli bychom tedy přestat psát. Stále nám ale nic nezaručí, že obě napsané posloupnosti slov nebudou stejné. Proto budeme dále požadovat, aby v cílovém stavu byla obě rozepsaná slova různá. Tím zaručíme, že se obě posloupnosti slov budou lišit alespoň v posledním slově. Tím sice omezíme počet řešení, co můžeme najít, ale to nám nevadí – pokud existuje řešení, ve kterém obě posloupnosti končí stejným slovem, tak jistě existuje i řešení, kde tomu tak není.
Počet prefixů slov bude nejvýše počet písmen ve slovníku plus jedna. Stavů tedy bude O(L2). Z každého stavu můžeme přejít do nejvýše 33 dalších stavů – můžeme přidat jedno z 30 písmen německé abecedy, nebo ukončit první, druhé nebo obě slova. Stavový prostor tedy můžeme prohledat s časovou i paměťovou složitostí O(L2) pomocí prohledávání do šířky nebo do hloubky. Najdeme tak nějakou cestu ze začátku do cíle a vypíšeme všechna přidaná písmena na této cestě. Pokud cestu nenajdeme, tak je němčina jednoznačná a hledané slovo neexistuje.
Zbývá ještě rozmyslet, jak budeme stavy reprezentovat. Nejprve najdeme všechny prefixy slov ze slovníku pomocí trie. Vrcholy trie snadno očíslujeme čísly od 0 do N-1, kde N je jejich počet. Stav pak můžeme reprezentovat jako dvojici čísel vrcholů, uchovávat je můžeme v dvourozměrném poli o velikosti N × N. Z trie také snadno poznáme vše, co o prefixech potřebujeme vědět, tedy jakými písmeny je můžeme rozšířit, a jestli jsou nějaké celé slovo.
Ještě si můžeme rozmyslet, že je tento algoritmus optimální,
alespoň při zvoleném způsobu analýzy.
Uvažujme slovník, co bude obsahovat jen dvě slova.
První z nich se bude skládat z N písmen a a druhé z N + 1 písmen a.
Víceznačné slovo bude existovat, ale nejkratší se bude skládat z N · (N + 1) písmen a.
Korektní algoritmus pro takovýto vstup musí vypsat kvadraticky dlouhý výstup,
takže určite neexistuje algoritmus, který by byl v nejhorším případě rychlejší než kvadratický.
 37-4-S Proměnné se probouzí (Zadání)
37-4-S Proměnné se probouzí (Zadání)
Seriál lze odevzdávat za snížený počet bodů až do konce školního roku. Řešitelům, kteří už čtvrtou sérii odevzdali, rozešleme vzorové řešení napřímo. Pokud chceš tuto sérii přeskočit a začít řešit další díl, můžeš si o vzorové řešení napsat na ksp@mff.cuni.cz.