Třetí série třicátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Dostává se k vám třetí číslo hlavní kategorie 37. ročníku KSP.

Letos se můžete těšit v každé z pěti sérií hlavní kategorie na 4 normální úlohy, z toho alespoň jednu praktickou opendatovou. Dále na kuchařky obsahující nějaká zajímavá informatická témata, hodící se k úlohám dané série. Občas se nám také objeví bonusová X-ková úloha, za kterou lze získat X-kové body. Kromě toho bude součástí sérií seriál, jehož díly mohou vycházet samostatně.

Autorská řešení úloh budeme vystavovat hned po skončení série. Pokud nás pak při opravování napadnou nějaké komentáře k řešením od vás, zveřejníme je dodatečně.

Odměny & na Matfyz bez přijímaček

Za úspěšné řešení KSP můžete být přijati na MFF UK bez přijímacích zkoušek. Úspěšným řešitelem se stává ten, kdo získá za celý ročník (hlavní kategorie) alespoň 50 % bodů. Za letošní rok půjde získat maximálně 300 bodů, takže hranice pro úspěšné řešitele je 150. Maturanti pozor, pokud chcete prominutí využít letos, musíte to stihnout do konce čtvrté série, pátá už bude moc pozdě. Také každému řešiteli, který v tomto ročníku z každé série dostane alespoň 5 bodů, darujeme KSP propisku, blok, nálepku na notebook a možná i další překvapení.

Zadání úloh

Praktická opendata úloha37-3-1 Robot (8 bodů)

Kevin si všiml, že v jeho gigantickém skladu s krabicemi to začalo vypadat nějak méně uspořádaně, než by si přál. Není to ale způsobené nesprávným rozložením krabic – ty jsou pořád umístěné pěkně do mřížky – nýbrž hromadami prachu, dřevěných pilin a jiných drobných částeček, které se při zběsilé manipulaci buldozerem z krabic uvolňují.

Velice ho tedy potěšilo, když na Vánoce dostal od rodičů nemodernější robotický vysavač značky Hroochba. Vysavač vypustil do skladu a nechal ho, ať si ho zmapuje.

Po pár dnech se ale vysavač z bludiště vrátil a sdělil Kevinovi, že má příliš málo paměti na to, aby si dokázal celý sklad zapamatovat (a na tak veliký sklad bude třeba určitě koupit víc vysavačů za víc $$$). Kevin se tedy rozhodl, že vysavač přeprogramuje na dálkové ovládání, a bude mu pro každou pozici posílat instrukce, kterým směrem se má posunout.

Vysavač to ale nejspíš dosti urazilo, protože když mu Kevin poslal nějakou instrukci, pokaždé se pohnul jiným směrem. Po odhalení téhle zlomyslnosti ho Kevin také začal podezírat, že má paměti ve skutečnosti dostatek na celý sklad (a sdělení o opaku bylo pouhým pokusem o to, aby mu Kevin koupil nějakého parťáka), neboť se vždy pohne co nejzákeřněji, tedy tak, aby ho nešlo dostat tam, kam Kevin chce.

Kevin se teď bojí, co by mohl pomstychtivý vysavač natropit ve skladu bez dozoru, ale než ho opraví, musí ho nejdřív chytit. Má připravených několik pastí a plánuje jednu z nich aktivovat, jenže neví, kterou zvolit. Chtěl by proto pro každou past zjistit, jestli do ní dokáže pomocí svého ovládaní vysavač navést.

Vysavač ale rozezná, kterou past Kevin aktivoval a pokusí se jí za každou cenu vyhnout – na každém políčku si zvolí směr pohybu (nutně jiný než ten, který mu Kevin poslal) vždy tak, aby se do pasti nikdy nedostal, je-li to možné. Tedy Kevin může jen odstranit jeden směr pohybu pro každé políčko a vysavač si vybere jeden ze zbylých směrů (pokud se tam může pohnout).

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku vstupu dostanete čísla R a S. Následuje R řádků délky S, které reprezentují mapu skladu. Znaky # označují neprůchozí políčka, znaky . jsou obyčejná volná políčka. Znak V označuje průchozí pole s vysavačem a znaky P průchozí pole s pastmi.

Formát výstupu: Pro každou past v pořadí dle jejího umístění (řádek, sloupec) vypište A, pokud je možné do ní vysavač chytit a N, pokud to nejde.

Ukázkový vstup: 
6 7
#######
#...PP#
#V##..#
#.###.P
#.###.#
#...P.#
Ukázkový výstup: 
ANNA
Vysvětlení ukázkového vstupu:

Do druhé pasti vysavač chytit nelze, neboť se z obou sousedních polí může rozhodnout uhnout na jedno z jejich dvou sousedních volných polí (a můžeme mu zabránit jít jen na jedno z nich).

Stejně to platí i pro jediné sousední pole třetí pasti a jeho dvě sousední pole.

Do první i čtvrté pasti lze vysavač chytnout, a to opakovaným zablokováním směru, který nevede na tu příslušnou past.

Praktická opendata úloha37-3-2 KSP-Nim-Vim (12 bodů)

Blíží se nový rok a je potřeba poslat novoroční přání. Musíme je všechna poslat do tiskárny. Naše tiskárna Nessie je ale trochu zvláštní. Je to obrovská obluda, která je velice vybíravá. Když Nessie dostane přání, tak si ho přečte, a pokud se jí líbí, tak ho vytiskne. A teď jsme zjistili, že z našich přání se Nessie nelíbí ani jedno!

Naštěstí nic není ztraceno, protože tiskárna je natolik chytrá, že má zabudovaný textový editor KSP-Nim-Vim. Tak jí můžeme poslat text, který se jí líbí, a soubor s instrukcemi pro editor, který z tohoto textu udělá naše novoroční přání. Jen ten editor je takový … svérázný.

V KSP-Nim-Vim-u existují čtyři typy instrukcí:

Pokud se pokusíme posunout kurzor mimo text nebo smazat neexistující písmeno, instrukce selže.

Vaším úkolem je napsat program v KSP-Nim-Vim-u, který převede jeden text na druhý. Jelikož Nessie edituje velmi pomalu, chceme provést co nejméně instrukcí měnících text. Posuny jsou zadarmo, stejně tak vypnutí Vim-u.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Formát vstupu: Na prvním řádku je text, který se Nessie líbí. Na druhém řádku je text, který chceme vytisknout.

Formát výstupu: Na každý řádek vypište jednu instrukci pro editování textu.

Ukázkový vstup: 
XcpYqSpH[]
S%{DMpRMH[]&@(zi-
Ukázkový výstup: 
2iS%
3i{DM
3x
3x
l
2iRM
l
l
l
3i&@(
3izi-
:wq

Jak vidíme z ukázkového vstupu, text můžeme převést 7 instrukcemi (pohyb je zdarma). Jde o nejmenší možný počet instrukcí, kterým můžeme text převést.

Teoretická úloha37-3-3 Hledání podmatice (13 bodů)

Dan si při přípravě na soustředění vzal na starost výběr místa pro noční hru v lese. Hra bude probíhat na veliké šachovnici (jak jinak) o rozměrech K×K, a jelikož je velice komplikovaná, nebude stačit jen tak nějaký volný plácek nebo mýtinka. Všechny terénní prvky musí přesně odpovídat velice podrobnému plánku, který dostal zadaný od ostatních orgů. Dokonce i orientace světových stran vůči plánku je pro hru nepostradatelně důležitá.

Dan ví, že při náhodném bloudění lesem to správné místo najde jen stěží. Vzal si proto satelitní fotografie z online map a nejmodernější AI na rozeznávaní terénních prvků. Les si rozdělil na čtvercovou síť velikosti N×N a pro každé pole si pomocí AI označil, co na něm leží.

Teď má dvě čtvercové matice – větší, velikosti N×N a menší, velikosti K×K – obsahující v každém poli jedno písmeno české abecedy (které značí terén na daném poli lesa nebo potřebný terén na daném poli plánku). Potřebuje už jen zjistit, jestli se matice s plánkem vyskytuje jako podmatice v lese, a pokud ano, alespoň jeden její výskyt najít. Pomozte mu!

Dejte si pozor na to, že některé řádky nebo sloupce matic mohou být stejné.

Toto je teoretická úloha. Není nutné ji programovat, odevzdává se pouze slovní popis algoritmu. Více informací zde.

Praktická opendata úloha37-3-4 Výhybky (12 bodů)

Experimentální úloha

Janči při přípravě na soustředění zavítal do Obchodu pro matfyzáky a díval se, co je na prodej. Obhlížel si výrobky, o kterých si nemyslel, že by je někde mohl sehnat. Nejprve si dal do košíku toroidní papíry, tolik potřebný materiál na soustředění. Prošel kolem nablýskaného Turingova stroje, důležité pomůcce k mnoha přednáškám. Nakonec se rozhodl koupit si nějakou funkci, ale bohužel se mu do batohu vlezla jen konstantní.

Po chvilce procházení po obchodě si všiml zapadlé krabice výhybkových hradel, kterou si koupil. Doma si ji spokojeně rozbalil a pomyslel si, co by se z nich všechno dalo sestrojit…

Pokud se s hradly ještě neznáte, může se hodit nahlédnout do Průvodce.

Výhybkové hradlo má tři vstupy a jeden výstup (logické hodnoty 0 nebo 1). Pokud je první vstup 1, vrátí druhý vstup, jinak třetí. Defakto vybíráme prvním vstupem jeden ze dvou zbývajících. Hradlo by se simulovalo následovně:

bool vyhybka(bool v1, bool v2, bool v3) {
    return v1 ? v2 : v3;
}

def vyhybka(v1: bool, v2: bool, v3: bool):
    if v1 is True:
        return v2
    else:
        return v3

Výhybková hradla můžeme skládat za sebe, tedy vstupem jednoho výhybkového hradla může být výstup druhého. Dále máme k dispozici konstanty 0 a 1, které můžeme do hradel zapojit.

Vašim úkolem bude sestrojit obvod – poskládání hradel za sebe, který bude mít výsledek 0 nebo 1 podle podúlohy:

Dále ještě definujme hloubku:

Hloubka obvodu je potom hloubka hradla udávající výsledek. Hloubka je analogií časové složitosti, protože v jednom kroku jsme schopni spočítat najednou všechny hradla, která už znají své vstupy. Vaše sestrojené obvody by měly mít hloubku nejvýše 100, což je zhruba logaritmicky k velikosti největších vstupů.

Lehčí variantaLehčí varianta (za 8 bodů): Část bodů dostanete, i pokud váš obvod bude mít libovolně velkou hloubku.

Toto je praktická open-data úloha. V odevzdávátku si necháte vygenerovat vstupy a odevzdáte příslušné výstupy. Záleží jen na vás, jak výstupy vyrobíte.

Aby si odevzdávátko mohlo přečíst vaši hradlovou síť, zaveďme si její značení. Jedno výhybkové hradlo budeme značit:

D1: Aa L P

Toto hradlo má jméno D1 a vstupy Aa, L a P. Když budeme chtít brát výsledek jako parametr, použijeme jeho jméno jako vstup:

D2: AX BX D1

Kromě toho existují speciální jména:

Formát vstupu: Vstup obsahuje jeden řádek se dvěma čísly – číslem podúlohy P, a počtem vstupních hodnot N.

Formát výstupu: Na řádky výstupu vypište popisy hradel ve tvaru [název]: [název] [název] [název], kde názvy se skládají z tisknutelných ASCII znaků. Váš obvod by měl odpovídat 0 nebo 1 podle zadání.

Bohužel Janči nemá hradel neomezeně, a proto si váš obvod musí vystačit s 10 000 hradly.

Ukázkový vstup: 
1 3
Ukázkový výstup: 
x03: in0 in2 0
result: in1 x03 0

Ve výstupu vidíme následující obvod:

Kdy vrací obvod 1? Pokud in0 nebo in1 je nastavené na 0, vracíme konstantní nulu, jinak vracíme in2. Abychom vrátili jedničku, tak všechny tři vstupy musí obsahovat jedničku. Obvod je tedy správně.

A jakou má obvod hloubku? Hradlo x03 bere vstupní hodnoty a konstanty s hloubkou 0, má tedy hloubku 1. Hradlo result má za svůj vstup s nejvyšší hloubkou hradlo x03, takže jeho hloubka je 2.

Teoretická úloha37-2-X1 Intervalové většiny (10 bodů)

Protože se nikomu nepodařilo X-kovou úlohu z druhé série vyřešit, rozhodli jsme se, že prodloužíme její deadline do konce 3. série. Navíc vydáváme následující nápovědu, která vám snad pomůže k řešení.

Může pomoci nejprve vyřešit následující úlohu:

Máme zadanou posloupnost prvků a1 až an a nějakou binární operaci ⊗ nad těmito prvky, o které víme jen, že je asociativní a že ji umíme počítat v konstantním čase. Vybudujte datovou strukturu, která umí pro zadaný interval posloupnosti mezi i a j spočítat

ai ⊗ ai+1 ⊗ …⊗ aj-1 ⊗ aj

v konstantním čase. Zkuste též zařídit, aby byla binární operace zavolána během dotazu jen jednou.

Následně upravte vaše řešení tohoto problému na řešení skutečné úlohy. K tomu pomůže několik šikovných vlastností nadpolovičních většin.

Seriálová úloha37-3-S Parsery vrací úder (15 bodů)

Letošním ročníkem vás bude provázet seriál. V každé sérii se objeví jeden díl, který bude obsahovat nějaké povídání a navíc úkoly. Za úkoly budete moci získávat body podobně jako za klasické úlohy série. Abyste se mohli zapojit i během ročníku, seriál bude možné odevzdávat i po termínu za snížený počet bodů. Vzorové řešení seriálu proto před koncem celého ročníku KSP uvidí jen ti, kdo už seriál odevzdali.

Dnešní díl seriálu věnujeme vyrábění finální části našeho překladače. Bude to program konzumující pole tokenů, které již dokážeme vytvořit ze vstupního programu díky naší práci z minulé epizody. Výstup bude opět pole, ale tentokrát instrukcí pro náš virtuální stroj z prvního dílu (doufáme, že ho stále máte).

Když se nad tím člověk zamyslí, vůbec nemusí být jasné, jak takovou transformaci efektivně provádět. Tento problém byl minulé století velice aktivně zkoumaný obor teoretické informatiky. V dnešní době už naštěstí máme velice bohatou a pěknou teorii formálních gramatik a tento problém je prakticky vyřešený.

My si dneska jedno takové řešení ukážeme. Bude se skládat ze dvou částí: První a hlavní část bude parser, který načte tokeny a vyrobí z nich stromovitou datovou strukturu které budeme říkat Abstract Syntax Tree (AST). Druhá, značně jednodušší část pak bude procházet tuto strukturu a budovat finální instrukce. Pokud si pamatujete analogii o zdolávání hory a částech překladače, AST by byl náš vrcholek.

AST

Abstract Syntax Tree je, jak název napovídá, strom, který abstraktně popisuje syntaxi programu. Česky se mu také říká syntaktický strom. Pokud jste v češtině dělali větný rozbor, náš parser bude tvořit velice podobnou strukturu z našeho programu. Pozor na to, že záleží na pořadí potomků jednotlivých vrcholů.

AST popisuje hierarchické vztahy mezi tokeny. Pro příklad si můžeme vzít vstup a + b. Ten by lexer přeložil na [NAME, PLUS, NAME] a takové pole budeme dnes parsovat do stromu v jehož kořeni je PLUS, v prvním potomku je NAME(a) a v druhém potomku je NAME(b). Výhoda stromové reprezentace je jednoznačnost. AST za nás řeší přednosti operátorů a uzávorkování. Například výraz 2 * 3 + 1 lze teoreticky přeložit na 2 různé stromy:

Dva různé stromy téhož výrazu

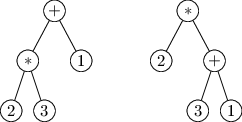
Parser za nás bude správně řešit přednosti operátorů a vždy vybuduje ten správný (v tomto případě levý) strom. Pozdější části překladače už přednosti operátorů vůbec nemusí řešit. Další důležitá vlastnost, kterou parser musí umět řešit, je asociativita operátorů. Ta rozhoduje, jak se mají operátory skládat, pokud jich je několik stejného druhu za sebou. Pro výraz 1 - 2 - 3 jde opět sestrojit 2 stromy:

Dva různé stromy téhož výrazu

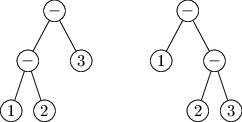
Operátor minus je asociativní zleva, takže operátory vlevo se vyhodnocují jako první. To nám jednoznačně vybírá strom vlevo. Prakticky všechny operátory jsou asociativní zleva. Jedinou výjimkou v našem jazyce je operátor přiřazení (a = b = c = a = (b = c)), v ostatních jazycích to navíc typicky bývá operátor mocnění (například v Pythonu a ** b ** c = a ** (b ** c)).

Zároveň stojí za to si ujasnit, jak budeme reprezentovat sekvenci příkazů (Příkaz je typicky jeden řádek. V C výraz ukončený středníkem. Anglický termín je statement.), neboli blok. V AST ji budeme reprezentovat jako vrchol, který má potomka pro každý příkaz v sekvenci (ačkoliv by se i na středník dalo dívat jako na binární operátor …). Poslední zajímavý případ jsou konstrukce typu if, for a while. if budeme reprezentovat jako vrchol, jehož první potomek je podmínka uvnitř kulatých závorek. Druhý syn je blok kódu, který se provede, pokud je podmínka pravdivá, třetí syn je blok kódu, který se provede, pokud je podmínka nepravdivá. for a while fungují stejně, jen jim stačí pouze první blok. Ty budeme ale parsovat až v dalším dílu, teď se pojďme vrhnout na výrazy.

Rekurzivní sestup

Konečně máme dostatek kontextu, abychom se vrhli do samotného parseru. Budeme programovat parser rekurzivním sestupem, což je velice populární typ parserů používaný ve spoustě dospělých překladačů, jako třeba GCC nebo V8. Začneme tradičně s pomocnou třídou TokenScanner:

#include "token.hpp"
#include <cctype>
#include <vector>

struct TokenScanner {
  std::vector<Token> source;

  TokenScanner(std::vector<Token> s)
      : source{s} {}

  bool isAtEnd() { return source.empty(); }

  Token peek() {
    return source.empty() ? Token(TK_EOF)
                          : source[0];
  }

  void advance() {
    source.erase(source.begin());
  }

  bool check(TokenType type) {
    if (isAtEnd()) return false;
    return peek().type == type;
  }

  bool match(TokenType type) {
    return match(std::vector<TokenType>{type});
  }

  bool match(std::vector<TokenType> types) {
    for (TokenType type : types) {
      if (check(type)) {
        advance();
        return true;
      }
    }
    return false;
  }

  void consume(TokenType type, string &message) {
    if (!match(type)) {
      error(message)
    }
  }

  void error(string &message) {
    if (isAtEnd()) {
      std::cerr << "Error at the end: ";
    } else {
      Token token = peek();
      std::cerr << "Error on token " <<
        token_type_to_str(token.type) <<
        "(" << token.value << ")" <<
        " at " << token.row <<
        ":" << token.column << ": ";
    }
    std::cerr << message << "\n";
    std::exit(1);
  }
};

TokenScanner je velice podobný třídě StringScanner z minulého dílu. Za zmínění stojí nová funkce consume, která zkontroluje příští token, a pokud se jí nelíbí, celý překlad ukončí s chybou. Bude se nám hodit například pro kontrolu, že všechny závorky jsou správně ukončené.

Další důležitá pomocná část je reprezentace našeho AST. Ten budeme reprezentovat jako jednotlivé vrcholy kde každý vrchol bude mít typ a seznam potomků. Vrcholu v AST budeme říkat Expr:

enum ExprType {
  ET_LITERAL,
  ET_NAME,
  // binární operátory
  ET_MULTIPLY,
  ET_DIVIDE,
  ET_ADD,
  ET_SUBTRACT,
  ET_LESS,
  ET_LESS_EQUAL,
  ET_GREATER,
  ET_GREATER_EQUAL,
  ET_EQUAL,
  ET_NOT_EQUAL,
  ET_ASSIGN,

  // unární operátory
  ET_NEGATE,
  ET_NOT,

  // příkazy
  ET_BLOCK,
  ET_PRINT,
  ET_VAR,
  ET_IF,
  ET_WHILE,
  ET_FOR,
};

struct Expr {
  Expr(ExprType t, std::vector<Expr> ch)
      : type{t}, children{ch} {}

  Expr(ExprType t, std::string v)
      : type{t}, value{v} {}

  ExprType type;
  std::vector<Expr> children;
  std::string value; // pokud je number nebo name
};

Třída Expr si občas musí pamatovat hodnotu čísla nebo jméno proměnné. Pro tyto účely jsme na konec ještě přidali string value. Parsování čísel budeme pro jednoduchost ještě chvilku odkládat.

Pokud chcete, nebojte se třídu Expr strukturovat nějak jinak, zvlášť pokud programujete v nějakém jiném jazyku. V objektových jazycích se často využívá dědičnost, ve funkcionálních algebraické datové typy, nicméně v C++ je jednodušší se polymorfismu vyhnout.

Úkol 1 – Opáčko rekurze [3b]

Než se pustíme do psaní parseru, pojďme si napsat funkci, která AST vypíše na výstup (nebo převede na string). Chceme, aby byl výstup rozumně čitelný, ale hlavně jednoznačný. Jedna z nejčastějších chyb jsou špatně uzávorkované operátory, takže potřebujeme rozeznat a + (b + c) od (a + b) + c.

Přesný formát je na vás, doporučujeme něco, co vypadá jako původní program s doplněnými závorkami. I pokud programujete v nějakém jazyce, kde něco takového máte zabudované, tak prosím napište vlastní implementaci, která bude pravděpodobně méně ukecaná.

Teď se skutečně vrhneme na samotný parser. Použijeme naši oblíbenou programovací techniku: delegování většiny práce na neexistující funkce:

Expr parse(TokenScanner &ts) {
  std::vector<Expr> statements;

  while (!ts.isAtEnd()) {
    statements.push_back(statement(ts));
  }

  return Expr(ET_BLOCK, statements);
}

Všimněme si, že výsledek celého parsování vracíme jako kořen AST Expr. Každý program v našem jazyce je sekvence příkazů, takže parsování není nic jiného, než opakované parsování jednotlivých příkazů, dokud nenaparsujeme celý program. Jak ale naparsujeme jednotlivý příkaz?

Jeden z možných příkazů v našem jazyce je například klíčové slovo print, po kterém pokračuje výraz, který chceme vytisknout. To pro nás bude dobrý začátek:

Expr statement(TokenScanner &ts) {
  if (ts.match(TK_PRINT)) return printStatement(ts);
  ...
}

Opět používáme oblíbenou techniku. Jak tedy ale vypadá printStatement?

Expr printStatement(TokenScanner &ts) {
  Expr value = expression(ts);
  ts.consume(TK_SEMICOLON,
             "Expected ';' after value.");
  return Expr(ET_PRINT, {value});
}

Parsování výrazů je o něco složitější. Zde budeme muset řešit asociativitu a priority binárních operátorů. Operátory si podle priority rozdělíme do skupin: násobení a dělení mají větší prioritu než operátory sčítání a odčítání; ty mají přednost před porovnáváním, což už má přednost jen před přiřazením. Unární minus má prioritu před všemi binárními operátory, -a ? b by mělo vždy znegovat jen a, nehledě na to, co za operátor je ?.

Pro každou úroveň priority budeme mít vlastní funkci: assignment, comparison, addition, multiplication, unary a primary. Poslední skupina je pro výrazy, kde už není co řešit – konstanta, přístup k proměnné nebo závorky.

Trochu neintuitivně jako první zavoláme funkci assignment, protože má operátor přiřazení nejnižší prioritu:

Expr expression(TokenScanner &ts) {
  return assignment(ts);
}

Expr assignment(TokenScanner &ts) {
  Expr left = comparison(ts);

  if (ts.match(TK_EQUAL)) {
    Expr right = assignment(ts);
    return Expr(ET_ASSIGN, {left, right});
  }

  return left;
}

Funkci assignment sice voláme jako první, ale první, co v rámci parsování přiřazení děláme, je, že opět použijeme oblíbenou techniku a pokusíme se naparsovat o úroveň priority vyšší výraz. comparison bude identicky volat addition, addition hned volá multiplication a tak dále, dokud se nedovoláme až do primary. První začne ve skutečnosti tedy číst tokeny funkce primary, pak unary, pak multiplication, atd. V primary musíme najít číselný literál nebo proměnnou, která se začne po řetízku volání funkcí postupně vracet a nabalovat na sebe operátory:

Expr expression(TokenScanner &ts);
Expr unary(TokenScanner &ts);

Expr primary(TokenScanner &ts) {
  auto token = ts.peek();

  if (ts.match(TK_NUMBER)) {
    return Expr(ET_LITERAL, token.value);
  }

  if (ts.match(TK_NAME)) {
    return Expr(ET_NAME, token.value);
  }

  if (ts.match(TK_LPAREN)) {
    // návrat zpět na začátek řetězce funkcí
    Expr e = expression(ts);
    ts.consume(TK_RPAREN, "Expected ')'");
    return e;
  }

  ts.error("Unexpected token");
}

Expr unary(TokenScanner &ts) {
  if (ts.match(TK_MINUS))
    return Expr(ET_NEGATE, {unary(ts)});
  else if (ts.match(TK_NOT))
    return Expr(ET_NOT, {unary(ts)});
  else
    return primary(ts);
}

Expr multiplication(TokenScanner &ts) {
  Expr e = unary(ts);
  // ...
}

Expr addition(TokenScanner &ts) {
  Expr e = multiplication(ts);
  // ...
}

Expr comparison(TokenScanner &ts) {
  Expr e = addition(ts);
  // ...
}

Expr assignment(TokenScanner &ts) {
  Expr left = comparison(ts);
  if (ts.match(TK_EQUAL)) {
    Expr right = assignment();
    return Expr::Assign(left, right);
  }
  return left;
}

Expr expression(TokenScanner &ts) {
  return assignment(ts);
}

Při tomto návratu se každá funkce podobně jako assignment pokusí zavolat match, aby zkontrolovala, jestli jde načíst dalších pár tokenů a vyrobit nový vrchol v AST. Jelikož se při návratu funkce volají pozpátku, dává smysl, že jsme první zavolali parsování operátoru s nejnižší prioritou.

Zajímavá je funkce unary. Ta se nejprve pokusí ukrojit unární prefixové operátory ze začátku vstupu, a až potom samotný výraz. To odpovídá tomu, že operátory negace čísel (-) a binární negace (!) se píší před výrazem, na který působí.

assignment po naparsování levého operátoru zkusí, jestli vstup nepokračuje tokenem přiřazení, a pouze pokud ano, naparsuje pravý operand a vyrobí nový vrchol v AST. Podobně fungují všechny ostatní úrovně operátorů. Opět jako všechny ostatní funkce provede fallback na vyšší prioritu operátorů, pokud nic pěkného nenajde.

V primary nemáme nic složitého. Na samotném dně rekurze se pokusíme najít číslo nebo jméno proměnné. Alternativně pokud najdeme otevřenou závorku, zarekurzíme se úplně zpátky do assignment a potenciálně celé kolečko funkcí opakujeme. Bez tohoto kroku bychom místo rekurzivního sestupu měli pouze sestup.

Teď nám stačí pouze doplnit vnitřnosti všech funkcí. Začneme třeba s funkcí multiplication:

Expr multiplication(TokenScanner &ts) {
  Expr expr = unary(ts);

  while (ts.check(TK_STAR) || ts.check(TK_SLASH)) {
    Token op = ts.peek();
    ts.advance();
    Expr right = unary(ts);
    ExprType type = (op.type == TK_STAR)
                        ? ET_MULTIPLY
                        : ET_DIVIDE;
    expr = Expr(type, {expr, right});
  }

  return expr;
}

Funkce multiplication má zajímavý tvar. Potřebujeme totiž správně ošetřovat asociativitu operátorů * a / v případě, že jich je několik za sebou. Proto jsme museli vytvořit smyčku, která se točí, dokud na vstupu vidíme jeden z těchto operátorů. Zároveň je třeba si rozmyslet, že tyto operátory jsou asociativní zleva (tzn, 12 / 3 / 2 vyjde 2, nikoliv 12). Proto musíme přilepovat původní výraz jako levý operand nového výrazu. To nám zaručí, že strom, který budujeme vně této funkce, se bude naklánět doleva, jak jsme si ukazovali v příkladu u asociativity. Velmi podobná konstrukce bude uvnitř ostatních ostatních funkcí, všechny zbylé operátory jsou také asociativní zleva.

Úkol 2 – Parsování operátorů [4b]

Doplňte implementaci zbylých funkcí addition a comparison.

Než se do toho ale vrhnete, zkuste zvážit, jak chcete, aby se chovaly operátory porovnávání (<, <=, >, >=, ==, a !=). V klasických Céčkových jazycích vám nic nebrání napsat výraz jako a == b > b == c, srovnávací operátory dokonce mají vyšší prioritu než operátory rovnosti. Ostatní jazyky ale často mají jiná pravidla, například asociativitu těchto operátorů „zakazují“ a nutí programátora výraz explicitně uzávorkovat. V Pythonu se zas tyto operátory začnou chovat „nebinárně“ a umožní vám spojit porovnávání shora i zdola: a < b < c je to samé jako a < b && b < c.

Vyberte si nějaké chování, trochu ho popište a naimplementujte. Nemusí to být jedna z možností popsaných výše, ale neuznáváme nejjednodušší možnost, tedy klasickou asociativitu bez rozdělení priorit pro rovnost a srovnání.

Úkol 3 – Proměnné [4b]

Funkce primary už umí číst proměnné, ale zatím je neumíme definovat. Naprogramujte parsování přikazu definice proměnné. Syntaxe je var jmeno = hodnota;. Tedy klíčové slovo var, token TK_NAME jako jméno proměnné, operátor rovná se, pak výraz a nakonec středník.

Zbytek syntaxe dokončíme příště, když už máme funkční parser výrazů a printu, pojďme z něj udělat funkční kalkulačku!

Převod do instrukcí

Posledním kouskem stavebnice je naprogramovat převod ze syntaktického stromu do kódu, kterému rozumí náš stroj z prvního dílu. Převést strom do instrukcí může v některých překladačích zahrnovat mnoho dalších kroků, jako je například přiřazení typů všem vrcholům stromu. Náš minijazyk ale umí pracovat jenom s čísly, takže implementace bude relativně přímočará.

I když se to první pohled se nezdá, tak reprezentace programu stromem je se sekvencí zásobníkových instrukcí celkem příbuzná. Idea převodu je rekurzivně projít strom a v každém vrcholu:

U aritmetických operátorů to opravdu bude takto jednoduché:

void emit(std::vector<instruction> &program,
          Expression &expr) {
  for (auto& operand : expr.children) {
    emit(program, operand);
  }

  switch (expr.type) {
  case ET_ADD: {
    program.push_back(instruction{.op = OP_ADD});
  } break;
  case ET_MULTIPLY: {
    program.push_back(instruction{.op = OP_MUL});
  } break;
  case ET_SUB: {
    program.push_back(instruction{.op = OP_SUB});
  } break;
  // ...
  case ET_LITERAL: {
    // Tady konečně naparsujeme číslo ze stringu
    // :)
    int value = std::stoi(expr.value);
    program.push_back(instruction{
        .op = OP_PUSH, .value = value});
  } break;
  }
}

Přístup k proměnné nebo konstanta do toho schématu také zapadají, nemají žádné potomky, jen přidaná instrukce bude muset obsahovat ještě parametr. Například výraz (a + b) * 3 bychom převáděli přibližně následovně:

* emit(`(a + b) * 3`)
    * emit(`a + b`)
       * emit(`a`) -> OP_LOAD a
       * emit(`b`) -> OP_LOAD b
       -> OP_ADD
    * emit(`c`) -> OP_PUSH 3
    -> OP_MUL

U některých typů výrazů to ale začne být trochu komplikovanější. V našem případě unární minus (výraz -x) bude lepší převést na sekvenci OP_PUSH 0, emit(operand), OP_SUB. Výrazně zábavnější budou podmínky a cykly, které budou vyžadovat skoky, ale ty naštěstí zatím neumíme ani naparsovat.

Příkazy jako print a definice proměnné se na konci budou jen potřebovat zbavit hodnoty na zásobníku. Tady jsme si lehce naběhli, když jsme v prvním dílu zapomněli přidat instrukci OP_POP. Můžete si ji přidat, pokud jste tak už neučinili. Pokud chcete být puritáni a pracovat s tím, co máme, můžeme hodnotu přiřadit do nějaké proměnné, kterou uživatel nepoužívá. Nejjednodušší je pojmenovat pomocnou proměnou například <void>, nebo libovolné jiné nepovolené jméno.

Úkol 4 – Překlad do instrukcí [4b]

Naprogramujte funkci emit tak, aby podporovala všechny výrazy a příkazy které umíme naparsovat (tedy kromě if, while, for a operátorů &&, ||).

Při implementaci mějte na paměti:

Měl by vám seběhnout například následující program:

var a = 1 + 2 * 9 / -3;
print a;
var b = 0;
print ((a = 10) * (b = 4)) / a / b;
print (a = 0) >= a;
print !(b > (b = 0));

Abyste měli jak testovat funkčnost, propojte všechny fáze překladu s interpretrem. Program můžete načítat ze souboru, ale klidně ho můžete mít jen jako konstantu ve zdrojovém kódu. Pokud chcete, můžete mít překladač jako separátní program od interpretru, jen pak musíte naprogramovat mechanismus, který umožní ukládat instrukce do souboru. Výměnou za to získáváte volnost při výběru programovacího jazyka – na překladač se nevztahují žádná omezení na neinterpretované jazyky :)

Všechny 4 úkoly odevzdejte najednou jako jeden ZIP soubor obsahující všechen váš zdrojový kód. Nemusíte kód dělit podle podúloh. Oceníme i slovní popis zvoleného řešení, bohatě by měly stačit komentáře v kódu.

Když budete mít jakýkoliv dotaz nebo problém, tak se nebojte ptát na našem Discordu či pomocí emailu. Na rozdíl od běžných úloh KSP smíte sdílet svůj přístup s ostatními řešiteli. Řešení ale naprogramujte sami.

Prokop Randáček, Standa Lukeš & Ondra Machota