Recepty z programátorské kuchařky
Hledání v textu

Řetězec je v podstatě jakákoliv posloupnost symbolů zapsaná za sebou a s nimi budeme v této kuchařce pracovat. Každého napadne „vyhledávání v textu“ nebo „hledání jmen v telefonním seznamu“,  ale řetězce najdeme i na nižších úrovních informatiky. Například celé číslo zakódované v binární soustavě, které dostaneme na vstupu programu, je také jen řetězec nul a jedniček.

Jiný příklad použití řetězců (a algoritmů s nimi pracujících) najdeme v biologii. Například DNA není o mnoho více, než chytré uložení posloupnosti čtyř znaků/nukleových bazí – chceme-li hledat vzory anebo konkrétní podposloupnosti, bude se nám hodit znalost základních algoritmů pro práci s řetězci.

Nemáme bohužel šanci vysvětlit všechny algoritmy s řetězci, protože je příliš mnoho možných věcí, co s řetězci dělat. Převáděním řetězců na čísla (hešováním) jsme se věnovali v jiné kuchařce, v této se budeme soustředit na algoritmy, které se objevují spíše v práci s textem.

Kromě úvodu do práce s řetězci popíšeme dva stavební kameny textových algoritmů, což bude datová struktura pro slovníky – trie a vyhledání v textu s předzpracováním hledaného slova a jeho rozšíření pro více slov. S jejich znalostí pak bude mnohem snazší vymýšlet řešení složitějších, reálnějších problémů.

Jak řetězce chápat

Když programátor dělá první krůčky, často moc netuší, co s těmi řetězci vlastně může a nesmí dělat. V programovacím jazyce to je jasné – něco mu jazyk dovolí a na něco nejsou prostředky. Ale jak to je na úrovni ryze teoretické?

Jak jsme si řekli na začátku, řetězec bude posloupnost nějakých symbolů, kterým říkáme znaky. Tyto znaky jsou z nějaké množiny, které říkáme abeceda. Abeceda může být jen {0, 1} pro čísla v binárním zápisu, klasické { A-Z, a-z } pro anglickou abecedu anebo plný rozsah univerzální znakové sady Unicode, která má až 2³¹ znaků. Nezapomínejme, že nejenom písmena a číslice, ale i mezery a interpunkce jsou znaky!

Vidíme, že zanedbat velikost abecedy při odhadu složitosti by bylo příliš troufalé, a tak budeme velikost abecedy označovat |Σ|. Abeceda sama se v textech o řetězcích často značí řeckým Σ.

O znacích samotných předpokládáme, že jsou dostatečně malé, abychom s nimi mohli pracovat v konstantním čase, podobně jako s celými čísly v ostatních kuchařkách.

Nyní hlavní otázka – máme chápat řetězec jako pole znaků, nebo jako spojový seznam? Šalamounská odpověď: můžeme s ním pracovat tak i tak. Když budeme potřebovat převést řetězec na spojový seznam (protože se nám hodí rychlé přepojování řetězců), tak si jej převedeme. Tento převod nás samozřejmě bude stát čas lineárně závislý na délce řetězce. Budeme ji dále značit L; časová složitost převodu bude O(L).

Standardně se ale počítá s tím, že řetězec je uložen v poli někde v paměti (již od začátku algoritmu), takže ke každému znaku můžeme přistupovat v konstantním čase.

Jelikož jsme řetězce definovali jako posloupnosti, nesmíme zapomínat ani na prázdný řetězec ε. A když už máme řetězec, určitě máme i podřetězec – souvislou podposloupnost znaků jiného řetězce. Například BAR, RET, ε i KABARET jsou podřetězce slova (řetězce) KABARET; KAT však podřetězcem není.

Často nás budou zajímat dva zvláštní druhy podřetězců. Pokud ze slova odstraníme nějaký souvislý úsek na konci, vznikne podřetězec, kterému říkáme prefix (česky předpona), a pokud odstraníme nějaký souvislý úsek ze začátku, dostaneme suffix neboli příponu. RET je suffix slova KABARET, KABA je zase jeho prefixem.

Terminologie dovoluje zepředu i zezadu odstranit prázdný řetězec – to znamená, že slovo je samo sobě prefixem i suffixem. Pokud chceme mluvit o prefixech, suffixech nebo obecně podřetězcích, kde jsme museli alespoň jeden znak odtrhnout, označíme takové podřetězce jako vlastní.

Pro některá použití řetězců je důležité, abychom je mohli porovnávat – když máme řetězce R a S, chceme umět rozhodnout, který je menší a který je větší. Jaké přesně toto uspořádání bude, závisí na naší aplikaci, ale mnohdy se používá tzv. lexikografické uspořádání.

Pro lexikografické uspořádání potřebujeme nejprve zadané lineární uspořádání na znacích. Tím se myslí takové, kde jsou všechny prvky navzájem porovnatelné, a v podstatě to znamená, že jsou uspořádány v jedné řadě za sebou (kromě binárního 0 < 1 se často používá „telefonní“ A = a < B = b < … < Z = z, které je ovšem lineární až na velikost znaků).

Když máme zadané uspořádání na znacích, na všechny řetězce je rozšíříme následovně: Nejkratší je prázdný řetězec. Ostatní řetězce třídíme podle jejich prvního znaku. Jestliže se první znak shoduje, tak podle druhého znaku, atd. Pokud přitom znaky jednoho z řetězců dojdou dřív, prohlásíme tento řetězec za menší.

Platí tedy třeba ε< A < AUTO < AUTOBUS < AUTOGRAM < AUTOR < BAMBITKA < BARNABAS < Z.

Adresář pomocí trie

Typický „textový“ problém je udržování množiny řetězců – můžete si představit třeba slovník. Slova ve slovníku si chceme šikovně předzpracovat, abychom pak mohli efektivně odpovídat na otázky typu: „Je slovo S obsaženo ve slovníku?“ Můžeme také po předzpracování chtít přidávat nové položky, nebo i odebírat staré.

Pokud bychom nemuseli odebírat slova, můžeme použít hešování, které je rychlé a účinné. Více o něm najdete v hešovací kuchařce. Má však tu nevýhodu, že při velkém zaplnění se začne chovat pomaleji a mírně nepředvídatelně.

Ukážeme si jiné řešení, které je také asymptoticky rychlé a není ani příliš náročné na paměť. Využívá stromové struktury a říká se mu trie (vyslovujeme česky „tryje“ a anglicky jako část slova „retrieval“,  z něhož slovo trie vzniklo). V češtině se občas používá také označení „písmenkový strom“.

Trie bude zakořeněný strom. V prvním patře se bude větvit podle prvního písmene slova, ve druhém podle dalšího, a tak dále.

Obrázek vydá za tisíc definic, pojďme se podívat, jak vypadá trie pro slova AHOJ, AT, KSP, TRIE, TROUD, TYC, TYCKA. Pro přehlednost písmena místo na hrany kreslíme do následujících vrcholů:

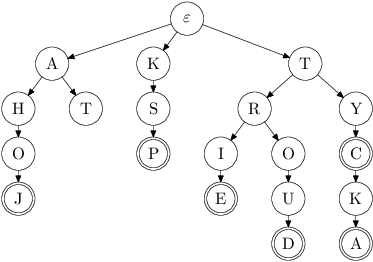
Všimněte si, že vrcholy v hloubce h (tedy v h-tém patře trie) odpovídají prefixům délky h zadaných slov. Například prefixy délky 2 jsou AH, AT, KS, TR a TY. Hrana mezi prefixy vede právě tehdy, lze-li jeden z druhého získat připsáním písmene na konec.

Jak bychom takovou trii postavili algoritmem? Přesně, jak jsme ji definovali: každé slovo ze slovníku budeme procházet znak po znaku, a bude-li nějaká hrana chybět, tak ji vytvoříme a pokračujeme dále podle slova.

Z takto popsané trie bohužel nepoznáme, kde končí slovo ze slovníku a kde končí jen jeho prefix. Standardní způsoby, jak to vyřešit, jsou dva: buď si do každého vrcholu přidáme informaci o tom, je-li koncem celého slova, nebo ne (jak je to naznačeno dvojitými kroužky v obrázku), anebo si rozšíříme abecedu o speciální znak, který se v ní předtím nevyskytoval – třeba $ – a pak všem slovům přilepíme tento $ na konec.

Budeme-li se později ptát, bylo-li slovo ve slovníku, po průchodu trií zkontrolujeme ještě, jestli z konečného vrcholu vede hrana odpovídající znaku $.

Ještě jsme si nerozmysleli, jak budeme v jednotlivých vrcholech trie reprezentovat hrany do delších prefixů. Abychom mohli vyhledávat skutečně lineárně, potřebovali bychom umět v konstantním čase odpovědět na otázku „má vrchol P potomka přes hranu se znakem c?“.

Abychom zajistili konstantní čas odpovědi, museli bychom mít v každém vrcholu pole indexované znaky abecedy. To ovšem znamená, že takové pole budeme muset vytvořit, a tedy alokovat |Σ| políček v každém znaku.

To zvýší paměťovou náročnost trie (a časovou náročnost její stavby) na O(D · |Σ|), kde D značí velikost vstupu, čili součet délek všech slov ve slovníku. To je naprosto přijatelné pro malé abecedy, ale už pro {A-Z, a-z} je tento faktor roven 52 a pro Unicode je taková alokace nemyslitelná.

Jak z toho ven? Můžeme oželet konstantní rychlost dotazu a použít namísto pole třeba binární vyhledávací strom nebo hešovací tabulku všech znaků, kterými aktuální prefix může pokračovat. Nebo můžeme každý znak velké abecedy zapsat pomocí několika znaků menší abecedy. Tou menší abecedou může být třeba {0, 1}. Tehdy nahradíme každý znak původní abecedy ⌈ log₂|Σ|⌉ novými (jeho zápisem ve dvojkové soustavě). Tím se časová slozitost konstrukce zlepší na O(D ·  log |Σ|) a časová složitost dotazu na slovo délky L zhorší na O(L ·  log |Σ|).

A jsme hotovi! S trií můžeme v lineárním čase odpovídat na dotazy „Vyskytuje se dané slovo ve slovníku?“, přidávat a odebírat další položky za běhu a nejen to – víc o tom ve cvičeních.

Poznámky

• Chcete-li algoritmus konstrukce trie vidět napsaný v Pascalu, podívejte se do knihy Algoritmy a programovací techniky.
• Triím se také říká prefixové stromy, což popisuje, že každý vrchol odpovídá prefixu některého slova ve slovníku.
• Kdybychom chtěli, mohli bychom pomocí trie vyhledávat v textu v lineárním čase. Můžeme přeci postavit slovník ze všech slov v daném textu, a pak procházet příslušnou trii. Má to ale pár háčků: jednak je často hledaný řetězec krátký, ale text se nevejde do paměti; jednak pokud bychom použili jako oddělovač mezery, mohli bychom hledat jen jednotlivá slova, a nikoli jejich konce nebo delší kusy věty.
• Asi se po poslední poznámce ptáte – existuje nějaká modifikace trie, která umí hledat libovolnou část textu? Ano, jmenuje se suffixový strom a jdou s ní dělat spousty krásných kousků. Říká se, že každou řetězcovou úlohu lze řešit v lineárním čase pomocí suffixových stromů. Víc se o nich dočtete třeba v knížce Krajinou grafových algoritmů.

Cvičení

• Řekněme, že chceme slovník na vstupu setřídit v lexikografickém pořadí (definovaném v sekci „Jak řetězce chápat“). Problémem pro klasické třídící algoritmy je to, že porovnání dvou řetězců není bohužel konstantně rychlé. Vymyslete způsob, jak setřídit takový slovník rychle pomocí trie.
• Komprese trie. Co kdybychom chtěli odstranit přebytečné vrcholy trie, tedy ty, v nichž se slova nevětví? Rozmyslete si, jestli by něčemu vadilo místo takovýchto cest mít jen jednotlivé hrany. Zesložití se konstrukce nebo vyhledávání? Mimochodem, je celkem jasné, že takováto komprimovaná trie přinese jen konstantní zrychlení dotazů i prostoru, a tak na soutěžích apod. stačí použít základní variantu.

Vyhledávání v textu

Začátek situace je asi zřejmý – máme na vstupu zadán dlouhý text a krátké slovo. Slovo si můžeme nějak předzpracovat, načež projdeme co nejrychleji text a nahlásíme jeden nebo všechny výskyty slova. Zajímají nás při tom i výskyty, které se navzájem překrývají: v textu NANANA se slovo NANA vyskytuje dvakrát. Často se hovoří o „hledání jehly v kupce sena“, pročež se textu přezdívá seno a hledanému slovu jehla. Délku jehly označíme J a délku textu S.

Představme si nejdříve hledané slovo jako spojový seznam, třeba slovo INSTINKT:

Mohli bychom text začít procházet znak po znaku a kontrolovat, zda se text shoduje s naším slovem/spojovým seznamem. Pokud by si znaky odpovídaly, skočíme na další znak z textu a i na další znak v seznamu. Co když se ale neshodují? Pak nemůžeme jen skočit na další znak textu – co kdybychom v textu narazili na slovo INSTINSTINKT?

Musíme se tedy vrátit nejen na začátek spojového seznamu, ale i zpátky v textu na druhý znak, který jsme označili jako odpovídající, a zkoušet porovnávat s jehlou znovu od začátku. To už naznačuje, že takto získaný algoritmus nebude lineární, protože se musí vracet zpět v textu o délku jehly.

Sice je předchozí popis skutečně v nejhorším případě složitý O(S · J), avšak stačí malá úprava a složitost přejde na lineární O(S+J). Ve skutečnosti algoritmus nezpomalovalo vracení se – za špatnou složitost mohl fakt, že jsme se vraceli příliš zpátky.

Třeba v našem příkladu s textem INSTINSTINKT se nemusíme vracet ve spojovém seznamu na začátek, jakmile načteme INSTINS. Mohli jsme se vrátit jen na druhý znak, tedy do prvního N, a pak kontrolovat, jaký znak pokračuje dál. Když následuje S jako v našem případě, můžeme pokračovat dále v čtení a nevracíme se v textu. Kdyby text byl jiný, třeba INSTINB, vrátili bychom se po načtení B na začátek spojového seznamu a v textu bychom pokračovali dále bez zastavení.

Pro každý znak ve spojovém seznamu si tedy určíme políčko spojového seznamu, na které skočíme, pokud se následující znak v textu liší od toho očekávaného. Pořadové číslo tohoto políčka nám poradí tzv. zpětná funkce F, což bude funkce definovaná pomocí pole, kde F[i] bude pořadové číslo políčka, na které se má skočit z políčka číslo i. Porovnávat pak budeme s následujícím znakem. Pokud F[i] = 0, znamená to, že máme začít porovnávat úplně od prvního znaku jehly.

Pokud máte rádi grafovou terminologii, můžete se na náš spojový seznam dívat jako na graf a hovořit o zpětných hranách.

Zatím jsme ale přesně nepopsali, na které políčko přesně bude zpětná funkce ukazovat. Nechť chceme určit zpětné políčko pro druhé N ve slově INSTINKT. Pracujeme teď s prefixem INSTIN. Selsky řečeno, chceme najít „konec slova INSTIN takový, že je stejný, jako začátek slova INSTIN“.

Abychom náš požadavek upřesnili, zamyslíme se nad zpětným políčkem pro jiné slovo. Co kdyby jehlou bylo slovo ABABABC a my určovali zpětné políčko pro ABABAB? Kdybychom ukázali na první písmenko B, nebylo by to správně, protože pak bychom pro text ABABABABC nezahlásili výskyt jehly, což je jasná chyba. Musíme se vrátit už na ABAB!

Zajímá nás tedy ne libovolný suffix, který je stejný jako začátek, ale nejdelší takový konec/suffix. A ještě navíc ne jen ten nejdelší, ale nejdelší „netriviální“ – slovo INSTIN je samo sobě prefixem a suffixem, ale zpětná funkce pro N by se neměla cyklit, měla by vést zpátky.

Řekněme to tedy znova, zcela formálně: pokud bychom právě určovali hodnotu zpětné funkce pro znak číslo i, kterému odpovídá prefix P, pak její hodnota bude délka nejdelšího vlastního suffixu slova P, pro který ještě platí, že je zároveň prefixem P.

Pro slovo INSTINKT vypadá spojový seznam se zpětnou funkcí (zakreslenou pomocí ukazatelů) takto:

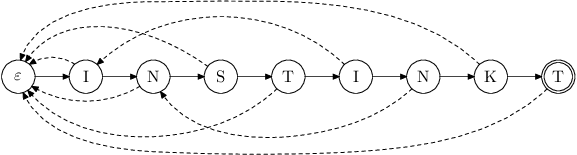
Nyní vyvstávají dvě otázky: Jakou to má celé časovou složitost? A jak spočítat zpětnou funkci?

Poperme se nejdříve s tou první. Pro každý znak vstupního textu mohou nastat dva případy: Buď znak rozšiřuje aktuální prefix, nebo musíme použít zpětnou funkci. První případ má jasně konstantní složitost, druhý je horší, neboť zpětná funkce může být pro jeden znak volána až J-krát.

Při každém volání však klesne pořadové číslo aktuálního stavu (políčka) alespoň o jedna, zatímco kdykoliv stav prodlužujeme, roste jen o jeden znak. Proto všech zkrácení dohromady může být nejvýše tolik, kolik bylo všech prodloužení, čili kolik jsme přečetli znaků textu. Celkem je tedy počet kroků automatu lineární v délce textu, tj. O(S).

Konstrukci zpětné funkce provedeme malým trikem. Všimněme si, že F[i] je přesně číslo stavu, do nějž se dostaneme při spuštění našeho vyhledávacího algoritmu na řetězec, který tvoří prefix délky i z jehly bez prvního znaku.

Proč to tak je? Zpětná funkce říká, jaký je nejdelší vlastní suffix daného stavu, který je také stavem, zatímco políčko, ve kterém po i krocích skončíme, označuje nejdelší suffix textu, který je stavem. Tyto dvě věci se přeci liší jen v tom, že ta druhá připouští i nevlastní suffixy, a právě tomu zabráníme odstraněním prvního znaku.

Takže F získáme tak, že spustíme vyhledávání na část samotné jehly. Jenže k vyhledávání zase potřebujeme funkci F. Jak z toho ven? Budeme zpětnou funkci vytvářet postupně od nejkratších prefixů. Zřejmě F[1] = 0. Pokud již máme F[i], pak výpočet F[i+1] odpovídá spuštění automatu na slovo délky i a při tom budeme zpětnou funkci potřebovat jen pro stavy délky i nebo menší, pro které ji již máme hotovou.

Navíc nemusíme pro jednotlivé prefixy spouštět výpočet vždy znovu od začátku – (i+1)-ní prefix je přeci prodloužením i-tého prefixu o jeden znak. Stačí tedy spustit algoritmus na jehlu bez prvního znaku a sledovat, jakými stavy bude procházet – to budou přesně hodnoty zpětné funkce.

Vytvoření zpětné funkce se nám tak nakonec zredukovalo na jediné vyhledávání v textu o délce J - 1, a proto poběží v čase O(J). Časová složitost celého algoritmu tedy bude O(S+J). Dodáme už jen, že tento algoritmus poprvé popsali pánové Knuth, Morris a Pratt a na jejich počest se mu říká KMP. Naprogramovaný bude vypadat následovně (čtení vstupu jsme si odpustili):

jehla = "INSTINKT"
seno = "INSTINSTINKTINSTINKT"
J = len(jehla)
S = len(seno)
F = [None] * J  # Zpětná funkce

def krok(i, znak):
    if i < J and jehla[i] == znak:
        return(i + 1)
    elif i > 0:
        return krok(F[i - 1], znak)
    else:
        return 0

# Konstrukce zpětné funkce
F[0] = 0
for i in range(1, J):
    F[i] = krok(F[i - 1], jehla[i])

# Procházení textu
stav = 0
for i in range(S):
    stav = krok(stav, seno[i])
    if stav == J:
        print(i - J + 1, "až", i)

var
  Slovo: array[1..J] of char;        { jehla }
  Text: array[1..S] of char;          { seno }
  F: array[1..J] of integer;    { zpětná fce }
  I, stav: integer;          { pomocné proměnné }

  function Krok(I: integer; C: char): integer;
  begin
    if (I < J) and (Slovo[I+1] = C) then
      Krok := I + 1
    else if I > 0 then
      Krok := Krok(F[I], C)
    else
      Krok := 0;
  end;

begin { konstrukce zpětné funkce }
  F[1] := 0;
  for I := 2 to J do
    F[I] := Krok(F[I-1], Slovo[I]);
  { procházení textu }
  stav := 0;
  for I := 1 to S do begin
    stav := Krok(stav, Text[I]);
    if stav = J then
      writeln(I);
  end;
end.

Poznámky

• Pro anglický nebo český text je použití takto sofistikovaného algoritmu skoro škoda, protože v obou jazycích se stává jen málokdy, že bychom měli několik slov spojených dohromady. Prakticky bude stačit i na začátku zmíněný naivní algoritmus. Na soutěžích a olympiádách ale pište raději algoritmus KMP.
• Hešování lze použít i na vyhledávání řetězce v textu. Obzvláště vhodné jsou na to rolling hash functions (neboli „okénkové hešovací funkce“), které umí v konstantním čase přepočítat heš, ubereme-li nějaký znak na začátku a přidáme-li jiný na konci – jako kdybychom se dívali na text skrz posouvající se okénko.

Cvičení

• Rozmyslete si, že když vyhledáváme více slov, ne jen jedno, a algoritmus musí vypsat všechny výskyty na výstup, můžeme se dobrat vyšší než lineární složitosti v závislosti na vstupu. Na čem potom taková časová složitost také záleží?
• Vymyslete nějakou vhodnou okénkovou hešovací funkci pro vyhledávání jedné jehly.

Vyhledávání jehelníčku

Co kdybychom neměli jen jednu jehlu/hledané slovo, ale celý jehelníček, čili seznam hledaných slov? I to lze řešit podobnou metodou, jakou jsme hledali jedno slovo. Tento algoritmus se nazývá po tvůrcích algoritmus Aho-Corasicková a spočívá v tom, že jednoduchý spojový seznam nahradíme trií a do trie opět přidáme zpětné hrany.

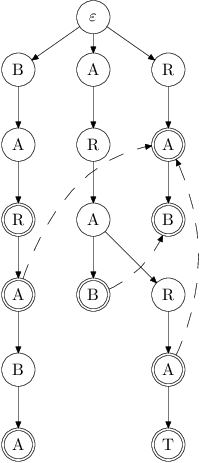
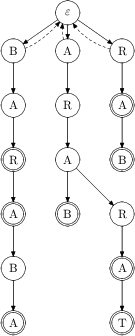
Budeme postupovat podobně jako u KMP. Nejprve naskládáme jehelníček do trie. Pro příklady v této kuchařce použijeme jehelníček ARAB, ARARA, ARARAT, BAR, BARA, BARABA, RA a RAB.

Dalším krokem v KMP bylo sestrojení zpětných hran. Nejprve jsme sestrojili zpětnou hranu pro první znak slova, pak pro druhý atd. V trii to bude o něco složitější.

Na první pohled se může zdát, že bychom mohli automat sestrojit tak, že bychom vyrobili KMP pro první slovo, pak KMP pro druhé slovo s využitím struktury prvního atd., ale to má háček.

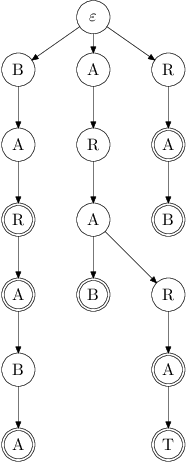
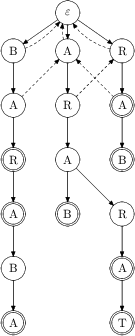
Zpětné hrany totiž nemusí vést do předka. Například pro slovo BARAB povede zpětná hrana do slova ARAB, z toho do slova RAB a z toho do B. Kdybychom ale zkonstruovali automat výše popsaným způsobem (a začali slovem BARAB), nebude existovat v trii ani ARAB, ani RAB, takže bychom vedli zpětnou hranu chybně do B.

Můžeme se ale opřít o stejný trik, jako při konstrukci KMP. Budeme opět vyhledávat nejdelší vlastní suffix. Kam dojde výpočet po jeho vyhledání, tam povede zpětná hrana.

Zkusíme tedy nejprve sestrojit celou trii a pak postupně vyhledat nejdelší vlastní suffix pro každé ze slov. Ouha, to ale také nefunguje. Když začneme slovem BARABA, a budeme tedy vyhledávat ARABA, nalezneme v trii úspěšně prefix ARAB, ale ARABA již v trii není. Měli bychom přejít ze slova ARAB po zpětné hraně, ale tu ještě nemáme zkonstruovanou.

Rozdělíme si trii na vrstvy – první znaky slov budou první vrstva, druhé znaky budou tvořit druhou vrstvu atd., až i-té znaky slov budou tvořit i-tou vrstvu.

Zpětná hrana jistě povede do kratšího slova. Z i-té vrstvy tak povede do vrstvy s nižším pořadovým číslem. Pokud tedy budeme zpětné hrany konstruovat po vrstvách, dojdeme kýženého výsledku.

Ještě zbývá otázka, jak konstruovat zpětné hrany efektivně, když je musíme vyrábět po vrstvách. Mohli bychom prostě vzít slovo, pro které hledáme zpětnou hranu, utrhnout mu první znak a vyhledat. Jenže to budeme dělat spoustu práce zbytečně.

Například pro slovo BARABA bychom mohli vyhledávat ARABA v již zkonstruované části automatu, ale proč to dělat celé, když jsme při konstrukci předchozí vrstvy vyhledávali ARAB při konstrukci zpětné hrany pro BARAB?

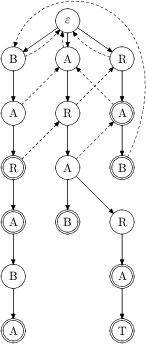
Při konstrukci další zpětné hrany tedy najdeme akorát, kde jsme minule skončili, a odtamtud pokračujeme dál. Jak to najdeme? Z otce našeho vrcholu tam přece vede zpětná hrana. Takže můžeme postup shrnout do bodů:

1. c = poslední znak slova (znak stavu P, pro který hledáme zpětnou hranu);
2. přesuneme se do otce;
3. přesuneme se po zpětné hraně;
4. dokud neexistuje syn se znakem c nebo nejsme v kořeni, přesouváme se po zpětných hranách;
5. pokud existuje syn se znakem c, natáhneme do něj zpětnou hranu z P, jinak ji natáhneme do kořene.

Automat je zkonstruován. Časová složitost konstrukce sestává z konstrukce trie v O(J · |Σ|), resp. O(J ·  log |Σ|) (pokud použijeme binární strom ve vrcholech) a z předpočítání zpětných hran. Při předpočítávání uděláme nějaký konstantní počet operací pro každý vrchol (celkem tedy O(J)) a také paralelně vyhledáváme všechny jehly z jehelníčku, jejichž vyhledání nás stojí O(J), resp. O(J ·  log |Σ|).

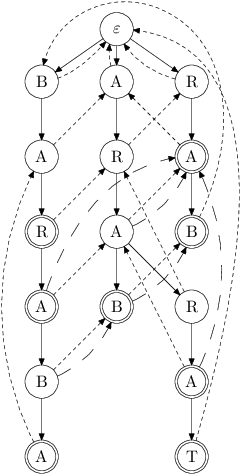
Tedy konstrukce trvá celkem O(J · |Σ|), resp. O(J ·  log |Σ|), paměťová náročnost je stejná jako u trie – O(J · |Σ|), resp. O(J), přidali jsme jen O(J) zpětných hran.

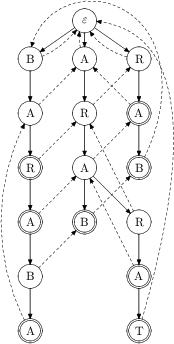
Zkusme tedy automatem projít text BARABARARAT. Ohlásí postupně nález slov BAR, BARA, BARABA, BAR, BARA, ARARA a ARARAT.

Nenalezl však všechno. Chybí mu např. ARAB, který začíná druhým znakem a končí pátým. Dále chybí několik výskytů RA a jeden RAB.

Když byl algoritmus na pátém znaku, byl ve stavu BARAB, jehož suffixem je ARAB. Obecně na suffixy zapomínáme. Na rozdíl od KMP, kde suffix aktuálního stavu nikdy nebyl jehla, tady jehlou být může.

V každém stavu bychom tedy měli projít všechny suffixy a zkontrolovat je, jestli náhodou nejsou jehlami. Jak najdeme všechny suffixy? Projdeme postupně po zpětných hranách až do kořene. Má to jen jeden problém – je to pomalé.

Představme si například slovník obsahující A a AAAA...A (délky J - 1). Budeme-li jím vyhledávat v textu AAAA...A délky S > J, projdeme prakticky pro každý znak až J - 1 zpětných hran, čímž složitost naroste až na nepoužitelných O(S · J).

Všimněme si však, že většinou zpětných hran jsme prošli úplně zbytečně. Předpočítáme si tedy zkratky – z vrcholu vede zkratka do nejdelšího jeho suffixu, který je jehlou. Na obrázku jsou vyznačeny dlouze čárkovanými šipkami.

Předpočítání zpětných hran časovou složitost konstrukce automatu jistě nezhorší, neboť vyžaduje v nejhorším případě projít všechny zpětné hrany ještě jednou.

Potřebujeme-li ohlásit všechny výskyty slov včetně pozice, kde se nacházejí, jsme hotovi. Výsledná časová složitost prohledávání bude O(S + O), resp. O(S ·  log |Σ| + O), kde O je velikost výstupu – počet výskytů všech slov.

Celková časová složitost prohledávání včetně stavby automatu tedy bude O(O + S + J · |Σ|), resp. O(O + (S+J) ·  log |Σ|).

Jak velký může být výstup? Obecně až S². Extrémně velký výstup je možné vygenerovat třeba slovníkem obsahujícím všechny prefixy slova AAAA...A délky S a senem taktéž AAAA...A délky S. Automat pak hlásí výskyt pro každé podslovo, kterých je řádově S².

Pokud nám stačí u každého slova jen počet výskytů, nemusíme zoufat – závislost na počtu výskytů umíme odstranit.

Použijeme trik – na každé pozici započítáme pouze nejdelší jehlu, která tam končí (u každé jehly si budeme udržovat čítač). Nebudeme tedy v každém kroku poskakovat po zkratkách až do aleluja, ale maximálně jednou. Díky tomu nám z časové složitosti zmizí velikost výstupu.

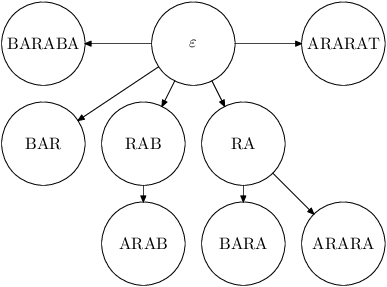
V našem příkladu se senem BARABARARAT tedy na konci budeme mít uloženo, že ARAB se vyskytnul 1×, ARARA 1×, ARARAT 1×, BAR 2×, BARA 2× a BARABA 1×. RA a RAB nemají hlášený žádný výskyt.

Nyní si zkonstruujeme strom jenom ze zkratek a pro každý vrchol spočítáme součet celého jeho podstromu.

Tedy po přepočtu bude mít RA tři výskyty a RAB jeden výskyt; celkový počet výskytů pak bude 12.

Poznámky

• Dalším krokem po KMP a Aho-Corasickové jsou konečné automaty a regulární výrazy, o kterých jsme měli seriál ve 23. ročníku.
• Není moc rozumné snažit se implementovat Aho-Corasickovou v rozumné době například při soutěži, pokud tento algoritmus nemáte opravdu pod kůží. Radši zkuste použít hešování, pokud budete něco takového potřebovat.

Cvičení

• Redukci o velikost výstupu můžeme provést i pro případ, kdy výstup nebudeme vypisovat, ale stačí nám mít jej uložený v paměti. Vymyslete vhodnou úpravu triku s čítačem.
• Zkuste si implementovat Aho-Corasickovou vlastnoručně ve svém oblíbeném jazyce, abyste si byli jisti, že doopravdy chápete všechny záludnosti tohoto algoritmu.

Martin Böhm, Jan Matějka, Martin Mareš a Petr Škoda