Recepty z programátorské kuchařky
Těžké problémy
Aktuální verze kuchařky: březen 2019
Občas se v informatice potkáme s problémem, který nám připadá skutečně těžký, s problémem, na který zatím nikdo nezná efektivní algoritmus. V tomto textu se pokusíme lépe si vysvětlit, co vlastně pro informatika znamená sousloví těžký problém.
Úvod a třída problémů P
Když mluvíme o efektivních algoritmech řešících nějaký problém, tak většinou máme na mysli algoritmus běžící v nějakém polynomiálním čase ve vztahu k velikosti vstupu. Například pro problém se vstupem velikosti N to jsou algoritmy, jejichž časovou složitost v nejhorším případě lze omezit shora nějakým polynomem závisejícím na N (sem spadají časové složitosti jako třeba O(N), O(N log N), nebo i O(N5)). Jestliže v základech časové složitosti tápete, nahlédněte do naší kuchařky o složitosti.
Pokud na problém existuje alespoň jedno známé polynomiální řešení, tak o problému můžeme prohlásit, že leží ve třídě P, neboli skupině úloh řešitelných v polynomiálním čase (třída tu je jen pomocné označení pro nekonečnou množinu). Stále můžeme problém zkoumat a nacházet rychlejší polynomiální řešení, ale pro teorii složitosti stačí, že máme alespoň nějaké.
Jak je to ale s úlohami, u kterých žádný polynomiální algoritmus neznáme? To mohou být třeba problémy, kde nejlepší známé řešení vede přes vyzkoušení všech možností, a jehož časová složitost je tak třeba O(2N), neboli exponenciální. Je důležité si uvědomit, že funkce jako 2N rostou mnohem rychleji, než jakékoliv polynomiální funkce (na názornou tabulku se můžete podívat do již zmíněné kuchařky o složitosti).
I takové problémy chceme nějakým způsobem zařadit do hierarchie složitostních tříd. Než tak ale učiníme, uděláme si malou odbočku – co kdyby nám někdo k problému poskytl i nápovědu, nějaký tahák?
S mapou v bludišti
Představme si, že jsme v bludišti a hledáme nejkratší cestu ven. Můžeme určitě použít prohledávání do šířky a cestu najít v čase lineárním k velikosti bludiště. To je asymptoticky nejlepší možné řešení, v nejhorším případě bude totiž bludiště jedna dlouhá nudle a i nejkratší cesta bude dlouhá lineárně vůči velikosti bludiště.
Jak by se změnila naše situace, kdybychom si ale od kamaráda půjčili tahák – mapu bludiště s vyznačenou nejkratší cestou? Pak by stačilo držet se této cesty a vyběhli bychom nejkratší cestou ven, aniž bychom kdekoliv ztráceli čas.
V nudlovém bludišti (nejkratší cesta má zhruba stejně vrcholů jako celý graf) jsme si vůbec nepomohli, takže je řešení asymptoticky stejně dobré. V alespoň trochu spletitém bludišti už budeme v cíli dříve než náš kamarád, který bloudí (prohledává) do šířky.
V tomto případě nám nápověda tedy zase tolik nepomohla, nalezení cesty z bludiště ven je totiž úloha, kterou umíme vyřešit v polynomiálním čase (patří do třídy P). Pojďme si ale úlohu trochu zkomplikovat a podívejme se, jestli s nápovědou tentokrát umíme dosáhnout lepšího výsledku než bez ní.
Opět jsme v bludišti, ale tentokrát jsou na všech stanovištích umístěny koláčky. Labyrint je to zvláštní, cesty se v něm nekříží, ale je tam plno nadchodů a podchodů (lze tedy říci, že je to obecný nerovinný graf).
Naším cílem je najít okružní cestu ze startovního místa zpátky na start, abychom každé stanoviště s koláčkem prošli právě jednou (protože víc než jeden koláček nám na žádném stejně nedají).
Kdybychom tady chtěli použít procházení do šířky, bylo by to opět možné – ale tentokrát bychom se museli mnohokrát vracet, protože posloupnost stanovišť (začátek, první, druhé) může být špatná, neboť nám může zablokovat další cestu. Zároveň ale posloupnost (začátek, druhé, první) už může být dobrá.
Nebude tedy už platit, že každý vrchol při prohledávání navštívíme maximálně jednou, ale každou posloupnost stanovišť navštívíme maximálně jednou. Takových posloupností je ale exponenciálně mnoho vzhledem k velikosti bludiště.
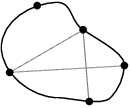
Pokud si pořídíme nový tahák, na kterém bude vyznačena optimální cesta přes všechna stanoviště, tak jsme na tom ale stále dobře. Tahák bude mít lineární velikost vzhledem k počtu stanovišť (cestou proběhneme každé z nich právě jednou) a umožní nám tak problém vyřešit v lineárním čase prostým následováním vyznačené cesty.
Našli jsme tedy problém, který nevíme jak vyřešit bez nápovědy v polynomiálním čase (a tedy ho nemůžeme s klidným svědomím zařadit do třídy P), ale s pomocí nápovědy už to umíme. Nedá se takovým způsobem definovat také nějaká třída složitosti? Dá! A to dokonce velmi důležitá.
Certifikáty a nedeterminismus
Vraťme se znovu k naší úloze s koláčky v bludišti. Zde celý problém tkví v tom, že se v některých chvílích prohledávání musíme rozhodnout, jakou z mnoha možností zkusíme nejdříve. Kdybychom pokaždé zvolili správně, tak zvládneme bludiště projít v lineárním čase.
Typický algoritmus, který napíšeme, většinou v případě více možností pokračování zvolí tu první (jeho volba je pevně určená, říkáme jí deterministická). Také ale můžeme přemýšlet o algoritmu, který si na každém takovém místě hodí kostkou a podle toho se rozhodne. Takový algoritmus nám na stejném vstupu může dát při různých spuštěních různé výsledky – jeho výpočet není „předurčen“, a proto mu říkáme nedeterministický.
Přidejme ale k nedeterministickému algoritmu naši nápovědu neboli certifikát. Je to nějaká (vzhledem k velikosti vstupu) polynomiálně velká informace. Můžeme si jej představit jako data, která náš program nalezne v pomocném vstupním souboru, ke kterému program z třídy P nemá přístup.
Certifikát nám pomůže v každém místě, kde nevíme kudy dál, zvolit tu správnou cestu. Bez něj bychom se museli zkusit vydat každou z nabízených možností, abychom objevili tu správnou, ale s jeho pomocí se vždy vydáme správně a existenci takové cesty ověříme rychle.
Pokud náš algoritmus s použitím takového věšteckého orákula (nebo křišťálové koule, chcete-li), jakým je certifikát, zvládne ověřit řešení problému v polynomiálním čase, říkáme o problému, že je nedeterministicky polynomiální, neboli že náleží do třídy NP.
Rozhodovací problémy a třída NP
Aby se nám problémy lépe formálně popisovaly a zařazovaly do tříd, omezíme se v dalším textu jen na rozhodovací problémy. To jsou vlastně otázky, na které existují jen dvě možné odpovědi: ano, nebo ne. Například:
- Existuje cesta z bludiště délky k?
- Je součet čísel 8+3 roven 5?
Jestli se obáváte, že to výrazně sníží množství problémů, které umíme řešit, tak se nemáte proč obávat – skoro vždy se rychlé řešení rozhodovacího problému dá převést na rychlé řešení příslušného vyhledávacího problému jen s nějakým malým zpomalením. Třeba nalezení délky nejkratší cesty z bludiště můžeme udělat pomocí binárního vyhledávání a opakovaného dotazu na existenci cesty délky k (detaily si jako cvičení domyslete).
V úvodu jsme si už řekli, že třída P představuje problémy řešitelné v polynomiálním čase (u rozhodovacího problému to bude znamenat, že existuje polynomiální algoritmus odpovídající na zadaný vstup korektně ano, nebo ne). U třídy NP si ale už musíme dát trošku pozor.
Třída NP je také třídou problémů. Problém do ní náleží ve chvíli, kdy existuje algoritmus a ke každému zadání, na nějž má být odpověď ano, navíc i certifikát, pomocí kterého zvládne algoritmus existenci řešení ověřit v polynomiálním čase. Ověřením se myslí to, že odpoví ano tehdy a jen tehdy, když řešení skutečně existuje.
Zde si dejme pozor na to, že definice nedovoluje „podvádět na druhou“, nemůžeme si do pomocného souboru prostě uložit ano a pak jej vypsat. Tak by se pak dal řešit libovolně složitý problém, i problémy mimo třídu NP!
Když si certifikát představíme jako ono orákulum, které nám vždy napoví správnou cestu, může být algoritmus nějaké nedeterministické řešení daného problému. Orákulum, ať bude napovídat jakkoliv špatně, ho nikdy nemůže přesvědčit o existenci nějakého řešení, pokud takové neexistuje. To je mimochodem důvod, proč certifikát nemůže být prostě jen ano: náš algoritmus se nesmí nechat zmást jakkoliv lživým orákulem, tím spíš takovým, které se ani neobtěžuje vymýšlet nám špatné odpovědi a jen nám tvrdí, že řešení existuje.
V reálné situaci (při dokazování, viz níže) si pak často za orákulum (za certifikát) zvolíme optimální řešení úlohy, kterého se stačí držet a najdeme hledanou odpověď (třeba dokážeme, že existuje cesta kratší než k).
Příslušnost do třídy NP tedy znamená schopnost s pomocí certifikátu dokázat existenci kladného řešení. (To vůbec nemusí znamenat, že dovedeme dokázat jeho neexistenci – to by byla zase jiná třída, které se říká coNP.)
Asi je vám jasné, že celá třída P (všechny problémy z ní) jsou součástí i třídy NP (stačí si za certifikát zvolit třeba prázdný soubor a problém vyřešit normálním polynomiálním algoritmem). A jak už jsme naznačili výše, existují i problémy, jež leží „ještě za třídou NP“, tedy takové, které neumíme vyřešit v polynomiálním čase ani s pomocí certifikátu. Ale dokazování toho, že takové problémy existují, už je nad rámec této kuchařky.
Je P rovno NP?
Ukázali jsme, že celé P leží uvnitř NP. Existuje však vůbec nějaký problém, který by byl v NP, ale nebyl by v P? To je otázka, jež trápí informatiky už mnoho let, jeden z nejslavnějších otevřených problémů informatiky.
Vezměme si za příklad problém z povídání o bludišti. Říká se mu Hamiltonovská kružnice.
Název problému: Hamiltonovská kružnice
Vstup: Neorientovaný graf.
Problém: Existuje v zadaném grafu kružnice procházející všemi vrcholy právě jednou?
Certifikát: Posloupnost vrcholů hamiltonovské kružnice.
Ověření v polynomiálním čase s certifikátem: Projdeme postupně vrcholy a ověříme, že jsou opravdu zapojeny do kružnice a kružnice je správné délky. Vrátíme ne, pokud tomu tak není.
Zatím nikdo nepřišel s řešením, které by nepoužívalo vůbec žádný certifikát. Dokonce zatím nikdo nenalezl problém, který by byl v NP, ale bez certifikátu už jej nelze řešit v polynomiálním čase. Kdyby takový neexistoval, třídy P a NP by se rovnaly. Díky převoditelnosti problémů v NP, které si nyní ukážeme, by dokonce stačilo najít polynomiální řešení bez certifikátu na jediný NP-úplný problém.
Převoditelnost a NP-úplnost
Když řešíme nějakou algoritmickou úlohu, obvykle přijdeme na nějaké přímé řešení využívající základních technik (prohledávání do šířky, dynamické programování, zametací přímka). Vzácně se může i stát, že v problému rozpoznáme problém jiný – občas lze geometrický problém převést na třídění čísel nebo umíme popsat situaci vhodným grafem.
Ukazuje se, že se ve třídě NP často vyplatí problémy převádět, neboť přímá řešení jsou zde vzácná. Dokonce tak můžeme i zjistit, do které z probíraných tříd problém patří.
Převodem budeme rozumět polynomiální algoritmus, který upraví vstup jednoho problému na vstup jiného problému. Musí navíc problémy převést tak, aby správná odpověď (ano nebo ne) na vstup prvního problému byla tatáž, jako správná odpověď na vstup druhého problému.
Jednoduchým převodem je úprava problému Existuje cesta z bludiště ze zadaného políčka délky d? na Existuje cesta v grafu délky c začínající v zadaném vrcholu?.
Do výstupního grafu za každou křižovatku dáme vrchol, za každou cestu mezi křižovatkami hranu a ke hraně si poznamenáme, jak dlouhá byla. Hodnotu c pak můžeme nechat stejně velkou jako d.
Pokud najdeme správnou cestu v tomto grafu, pak nutně podobná cesta je i v bludišti, a pokud cesta v grafu není, pak není ani v bludišti. Převod je tedy korektní.
Zadefinujme si nyní pojem, který nám bude sloužit jako zkratka za to, že problém je ve třídě NP, ale není zároveň lehký (v P). Nemůžeme jen tak ledabyle říci „je v NP a není v P“, protože to nevíme. To je právě ta slavná otázka.
Uděláme tedy krok stranou – budeme říkat, že problém je NP-úplný, pokud onen problém je v NP a zároveň jdou všechny ostatní problémy v NP převést na tento problém.
Všechny problémy v NP na něj jdou převést? Pokud tuto definici vidíte poprvé, asi to působí dost zvláštně – je těžké si představit, že všechny grafové, geometrické, počítací problémy, o kterých víte, že jsou v P (a tedy i v NP) jdou převést na nějaký NP-úplný superproblém.
Ale je to správně, ba co víc, Cookova věta říká, že existuje alespoň jeden takový problém. (Samotná definice NP-úplného problému nezaručuje, že takový problém vůbec existuje.)
Ukazuje se však, že není sám, jsou jich stovky. Dokazovat existenci dalších NP-úplných problémů je však o dost lehčí než dokázat Cookovu větu! Stačí totiž jen provést následující dva kroky:
- Dokázat, že problém je v NP – najít certifikát a polynomiální algoritmus, co jej využívá.
- Převést zadání libovolného NP-úplného problému na zadání našeho problému tak, že náš algoritmus vlastně vyřeší onen NP-úplný problém.
To postačí, protože pak libovolný jiný problém v NP nejprve převedeme na zvolený NP-úplný problém a pak pustíme námi vymyšlený převod. Zřetězení dvou polynomiálních algoritmů (převodů) je opět polynomiální algoritmus, takže podmínka převoditelnosti je splněna.
Ukážeme si důkaz NP-úplnosti jednoho problému na příkladu, pokud nám uvěříte, že již probíraný problém Hamiltonovská kružnice je NP-úplný. Nejprve zadefinujme jiný problém:
Název problému: Hamiltonovská cesta.
Vstup: Neorientovaný graf, dva speciální vrcholy x a y.
Problém: Existuje cesta z x do y (posloupnost vrcholů, ve které se žádné dva neopakují), která prochází každým vrcholem právě jednou?
Certifikát: Posloupnost vrcholů tvořící správnou cestu.
Řešení v NP: Projděme cestu z certifikátu a ověřme, že vrcholy jdou za sebou, je jich správný počet a žádný jsme nevynechali.

Důkaz NP-úplnosti: Převedeme předchozí problém (hamiltonovskou kružnici) na hledání hamiltonovské cesty. Uvažme graf G, ve kterém chceme najít hamiltonovskou kružnici.
Vyberme si libovolný vrchol v a vytvořme vrchol v', který bude kopií vrcholu v – do grafu přidáme hranu mezi u a v', pokud už v něm je hrana mezi u a v.
Na upravený graf zavoláme řešení problému Hamiltonovská cesta mezi vrcholy v a v'. Pokud taková cesta existuje, tak nutně v původním grafu G existuje hamiltonovská kružnice.
Cesta z vrcholu v' přesně odpovídá pokračováni kružnice poté, co přijde do vrcholu v.
Pseudopolynomiální algoritmy
Znáte problém batohu? Jeho varianty jsou oblíbené na programovacích soutěžích. Zadat se může třeba takto: mějme na vstupu seznam N dvojic kladných přirozených čísel, kde každá dvojice označuje váhu a cenu nějakého předmětu. Nakonec dostaneme na vstupu ještě číslo B, které udává nosnost našeho batohu.
Otázka zní: Jaký je nejcennější možný náklad, který přesto nepřesahuje váhový limit batohu?

Možná víte, že úloha jde řešit dynamickým programováním – vytvoříme si pole
podbatoh[] od 1 do B, kde podbatoh[i] je maximální hodnota,
kterou bychom si odnesli v batohu o nosnosti i. Postupně od první věci do
poslední pak projdeme celé pole podbatoh[] „zprava doleva“ od B do 1
a zkusíme, jestli je výhodnější do batohu vložit novou věc a volné místo doplnit
starými (optimální volné místo pro předchozí věci máme napočítané), nebo si
nechat jen ty staré. Tuto hodnotu pak zapíšeme jako aktuální pro váhu i na
místo podbatoh[i].
Po N průchodech tohoto pole dostaneme řešení pro všechny věci dohromady
na políčku podbatoh[B]. Celková složitost je O(NB), to je polynom,
algoritmus je tedy polynomiální.
Světe div se, toto řešení je ve skutečnosti exponenciální. Kde jsme v řešení udělali chybu? Nikde – naše složitost závisela na B, ovšem když se podíváme do vstupních dat, tak pokud jsou zapsána v binárním (nebo ternárním a vyšším) tvaru, zápis čísla B je veliký O(log2 B). Naše složitost však závisí na B = 2 log2 B, je tedy exponenciální vzhledem k velikosti vstupu.
Problém batohu, respektive jeho rozhodovací verze, je dokonce NP-úplný problém.
Algoritmům, které řeší nějakou úlohu a jsou polynomiální vůči hodnotě čísel na vstupu, ale exponenciální ve velikosti zápisu těchto čísel, říkáme pseudopolynomiální algoritmy. Některé další NP-úplné problémy mají pseudopolynomiální řešení (jako například Dva loupežníci níže), ale dá se dokázat, že na jiné problémy pseudopolynomiální algoritmus neexistuje (pokud P ≠ NP).
Mimochodem: pokud bychom na vstupu zapisovali čísla v unárním zápisu (tedy místo každého čísla by bylo třeba tolik hvězdiček, jakou hodnotu představuje), každý pseudopolynomiální problém by ležel v P.
Poznámky na závěr
Otázku „Je třída P rovna NP?“ se již snažilo rozlousknout mnoho matematiků a informatiků. Tato teorie přinesla spoustu zajímavých výsledků, například už se podařilo dokázat, že některými technikami tuto domněnku nelze nikdy dokázat, ani vyvrátit.
Kdyby platilo P = NP, pak by mnoho lidi zajásalo – spousta přirozených problémů, které nastávají i v reálném životě, by najednou byla řešitelná rychle. Navíc by krachlo dosavadní šifrování a bylo by možné najít rychle důkaz ke každému pravdivému tvrzení výrokové logiky.
Tato rovnost by se dala hypoteticky ukázat velice snadno – stačilo by najít jeden polynomiální algoritmus pro libovolný NP-úplný problém! Většina informatiků studujících složitost se však domnívá, že se třídy nerovnají.
To ale neznamená, že si to nemáte zkusit dokázat! Naopak, bojovat s NP-úplnými problémy je užitečné i v reálném světě – mnohdy jde vymyslet třeba dobrá aproximace řešení.
Například nenajdeme hamiltonovskou kružnici v polynomiálním čase, ale nalezneme nějakou relativně dlouhou kružnici, která nám v praxi může stačit, pokud podle ní třeba chceme vést náročný cyklistický závod.
O aproximacích je toho v literatuře napsáno mnoho zajímavého, pokud byste si o nich chtěli přečíst více v češtině, zkuste třeba kapitolu o NP-úplných problémech v knížce Průvodce labyrintem algortmů.
Více o třídě NP i o dalších aspektech složitosti můžete najít na stejné adrese, nebo zkuste vynikající anglicky psanou knížku Algorithms od profesorů exotických jmen Dasgupta, Papadimitriou a Vazirani.
Jak už jsme zmínili, existují i problémy, které jsou mimo P i NP, a dokonce existuje spousta různých dalších tříd problémů. Je jich celá zoologická zahrada – pěkný souhrn můžete najít na Complexity zoo.
Seznam NP-úplných problémů

Sedíte-li nad zatím nevyřešenou úlohou, kterou stále nemůžete rozlousknout, je možné, že bude NP-úplná. Abyste mohli mezi NP-úplnými úlohami převádět, tak je dobré znát jich aspoň hrstku, podle toho, je-li problém grafový, rovnicový, a tak dále.
V následujícím seznamu najdete několik úloh, které jsou zaručeně NP-úplné. Převody se nám sem už sice nevešly, ale většinu z nich (ne-li všechny) zvládnete vymyslet sami – zkuste to!
Název problému: Hamiltonovská kružnice
Vstup: Neorientovaný graf.
Problém: Existuje v zadaném grafu kružnice procházející všemi vrcholy právě jednou?
Název problému: Hamiltonovská cesta
Vstup: Neorientovaný graf, dva speciální vrcholy x a y
Problém: Existuje cesta z x do y (posloupnost vrcholů, ve které se žádné dva neopakují), která prochází každým vrcholem právě jednou?
Název problému: Splnitelnost
Vstup: Logická formule. Tu tvoří proměnné a logické spojky negace ¬, konjunkce ∧ a disjunkce ∨ . Například
Problém: Můžeme proměnným přiřadit hodnoty 0 nebo 1 tak, že výsledná vyhodnocená formule má hodnotu 1?
Název problému: Součet podmnožiny
Vstup: Seznam nezáporných celých čísel, speciální číslo k.
Problém: Existuje podmnožina čísel, jejíž součet je přesně k?
Název problému: Batoh
Vstup: Seznam dvojic nezáporných čísel, kde dvojice označuje hodnotu a váhu předmětu. Přirozené číslo b – nosnost batohu, přirozené číslo k.
Problém: Umíme vložit do batohu předměty o hodnotě alespoň k, aniž bychom přešli přes limit váhy b?
Název problému: Dva loupežníci
Vstup: Seznam nezáporných celých čísel.
Problém: Existuje rozdělení seznamu na dvě hromádky tak, že každé číslo bude v právě jedné hromádce a v každé hromádce bude stejný součet čísel?
Název problému: Klika
Vstup: Neorientovaný graf, číslo k.
Problém: Existuje v grafu úplný podgraf o velikosti k, tedy k vrcholů takových, že mezi každými dvěma z nich vede hrana?
Název problému: Nezávislá množina
Vstup: Neorientovaný graf, číslo k.
Problém: Existuje v grafu nezávislá množina vrcholů o velikosti k, tedy k vrcholů takových, že žádné dva z nich nejsou spojeny hranou?
Název problému: Trojbarevnost grafu
Vstup: Neorientovaný graf.
Problém: Lze vrcholy tohoto grafu obarvit třemi barvami tak, že spolu žádné dva vrcholy stejné barvy nesousedí?
Název problému: Rozparcelování roviny
Vstup: Seznam bodů v rovině, kde každý má navíc přiřazenu jednu z b barev, číslo k.
Problém: Umíme rozdělit rovinu pomocí k přímek tak, že v každé oblasti jsou jen body té samé barvy?
Název problému: 3D párování
Vstup: Seznam mužů, žen a zvířátek, následovaný seznamem kompatibilních trojic tvaru { muž, žena, zvířátko }. Tyto trojice říkají, která trojice muž, žena a zvířátko by se dohromady snesla.
Problém: Můžeme všechny muže, ženy a zvířátka z prvního seznamu rozdělit do trojic tak, že každá trojice je kompatibilní a každá bytost je právě v jedné trojici?