Recepty z programátorské kuchařky
Základní algoritmy
Aktuální verze kuchařky: září 2021
Tato naše kuchařka je nejzákladnější ze základních a je určena hlavně pro začínající řešitele. To však neznamená, že zkušenější řešitelé do ní nahlédnout nemůžou – třeba na nějakou konkrétní programátorskou techniku, kterou by si potřebovali osvěžit.
V první části kuchařky se seznámíme hlavně se základními principy programování, uchovávání dat v počítači a základy rychlé manipulace s nimi. Po přečtení této části bychom měli být schopní převést své myšlenky z hlavy na papír či do počítače a měli bychom vědět, proč je námi zvolený postup rozumný.
Druhá část nás poté seznámí se základními postupy, jak řešit určité konkrétní problémy. Naučíme se například, jak rychle vyhledávat v uspořádané posloupnosti hodnot nebo jak si pomocí předpočítání usnadnit řešení těžké úlohy.
Většinu klíčových částí se pokusíme též ukazovat v podobě zdrojového kódu ve dvou různých jazycích (v nízkoúrovňovém C, kde je zápis blízký tomu, jak počítač doopravdy pracuje, a v Pythonu, ve kterém se píše o něco příjemněji). Nebudeme ale probírat základy syntaxe těchto jazyků, ty si případně můžete nastudovat jinde.
Část první: Základní pojmy
Algoritmus a program
Pod tajemným slovem algoritmus se skrývá jen jiný výraz pro postup. Můžete si to představit jako příkaz od maminky „Běž do krámu, kup chleba, a když budou mít měkké rohlíky, tak jich vem tucet“. (A jako slušně vychovaní se tedy vydáte do krámu a koupíte tucet chlebů, protože měli měkké rohlíky :-))
Takovýto příkaz klidně můžeme nazvat algoritmem, ačkoliv to bude asi znít nezvykle – pojem algoritmus se totiž používá hlavně ve světě počítačů. Je to tedy nějaká posloupnost základních příkazů, která řeší nějaký problém. Výběr konkrétního programovacího jazyka rozhoduje o tom, jaké základní příkazy budeme mít k dispozici. Většinou jsou ale skoro stejné.
Mezi základní příkazy patří:
- Manipulace s daty v paměti (uložení či načtení hodnoty, detailněji v další kapitole).
- Provedení nějakého numerického výpočtu (+,-,*,/).
- Vyhodnocení nějaké konkrétní podmínky a odpovídající větvení programu: Pokud platí A, tak proveď B, jinak proveď C. Přitom B i C mohou být klidně celé bloky kódu, tedy libovolně mnoho dalších základních příkazů.
- Opakování nějakého příkazu: Dokud platí A, dělej B. Takové konstrukci říkáme cyklus a podobně jako u podmínky může být B blok kódu, který se celý opakuje.
- Vstup a výstup programu (typicky vstup od uživatele z klávesnice či načtení vstupu ze souboru; výstup pak může znamenat vypsání výsledku na obrazovku nebo třeba zapsání dat do souboru).
Z těchto základních stavebních kamenů se skládá každý algoritmus. Programem potom rozumíme realizaci algoritmu v nějakém konkrétním programovacím jazyce.
U složitějších programů se pak často setkáme s problémem, že budete mít nějakou posloupnost příkazů, která se bude na spoustě míst programu opakovat, což zbytečně prodlužuje a znepřehledňuje kód.
Řešením tohoto problému je použití funkcí. Funkci si můžeme představit jako nějakou pojmenovanou část programu (s vlastní pamětí), kterou můžeme opakovaně použít tím, že ji v různých částech programu zavoláme. Funkci při zavolání předáme parametry (například seznam čísel), které se dostanou do její vnitřní paměti.
Funkce pak na základě obdržených parametrů může provádět nějaké operace, při kterých pracuje se svojí vnitřní pamětí (mluvíme o lokální paměti, změny v ní se neprojeví nikde mimo funkci). Na konci nám funkce může vrátit nějaký výsledek. Pokud funkce během svého běhu změní i nějaká data v globální paměti, či provede nějakou globální operaci (například výpis textu na monitor), mluvíme pak o funkci s vedlejšími efekty (neboli side-efekty).
Konkrétním příkladem může být funkce, která nám spočítá odmocninu ze zadaného čísla. Ta dostane jako svůj parametr číslo, uvnitř si provede nějaký výpočet, o který se jako uživatel funkce nemusíme starat, a jako výstup nám vrátí spočtenou odmocninu.
Reprezentace dat v počítači
Celkem často si v průběhu výpočtu našeho algoritmu potřebujeme pamatovat nějaké hodnoty. K tomu nám programovací jazyky dávají nástroj s názvem proměnná. Ta představuje jakési pojmenované místo v paměti (přihrádku), do kterého si můžeme data ukládat a pak je odtud zase načítat.
Typickým příkladem může být počítání součtu čísel, která nám uživatel zadá na vstupu. Na začátku nejdříve do nějakého místa v paměti uložíme hodnotu 0. Poté postupně, jak nám uživatel zadává čísla, tuto proměnnou pokaždé přečteme, k její hodnotě přičteme nově zadané číslo a výsledek opět uložíme na stejné místo.
Takovéto použití jedné proměnné je velmi jednoduché (tak jednoduché, že ho takto podrobně do řešení KSPčka nepište, není to potřeba), ale také celkem omezené. Co kdybychom si chtěli pamatovat třeba celou zadanou posloupnost čísel? Mohlo by nám stačit vyrobit si spoustu různě pojmenovaných proměnných, ale nejde to lépe? Jde.
Jednotlivé proměnné se mohou kombinovat do složitějších konstrukcí, které obecně nazýváme datovými strukturami. Zkusíme si ty nejzákladnější představit.
Pole
První datovou strukturou, kterou si představíme a která se na výše nastíněnou
situaci náramně hodí, je pole. To představuje spoustu přihrádek
(proměnných) naskládaných v paměti za sebou, ke kterým typicky přistupujeme přes
jeden společný název pole a jejich pořadové číslo neboli index (jako NazevPole[0], NazevPole[1],
…). (Pozor, ve světě počítačů se velmi často indexuje od nuly, tedy první
prvek má v tomto případě index 0.)
Ve většině základních jazyků je pole jen statické, tedy v okamžiku jeho vytváření musíme počítači říct, jak ho chceme velké. Některé vyšší jazyky ale nabízejí i pole, které se dynamicky zvětšuje, takovou konstrukci si ukážeme ve druhé části kuchařky.
Abychom nebyli omezeni jen jedním rozměrem, můžeme si klidně vyrobit pole dvourozměrné (případně obecně n-rozměrné). Dvourozměrné pole je vlastně tabulka hodnot, nazýváme ji také někdy matice, a může se nám hodit například při reprezentaci různých map (plán bludiště) nebo, jak uvidíme níže, pro reprezentaci dalších datových struktur.
U pole již má smysl přemýšlet, jak dlouho bude která operace trvat. Díky tomu,
že jsou jednotlivé prvky v poli naskládané pevně za sebou, je snadné spočítat
umístění konkrétní přihrádky. Proto když se počítače zeptáme na obsah
přihrády pole[42], vrátí nám hodnotu ihned.

Tomu budeme říkat operace v konstantním čase a budeme značit, že trvá čas O(1). Efektivitu programu totiž nepočítáme v sekundách (protože každý z nás má asi jinak rychlý počítač), ale v počtu základních operací, které musí program řádově vykonat. Více o časové složitosti si můžete přečíst v kuchařce o složitosti, nejdříve však doporučujeme dočíst tuto kuchařku.
Přidání nového prvku na konec pole také zvládneme v konstantním čase. Problém je přidání nového prvku někam doprostřed (což se nám typicky stane, pokud budeme chtít udržovat hodnoty v poli seřazené a zároveň do něj vkládat nové). V takovém případě se totiž všechny prvky za vkládaným musí posunout o jednu pozici dál, aby se vkládaný prvek vešel na své místo. Taková operace tedy může pro pole délky N (čili pole obsahující N prvků) trvat řádově až N kroků, což zapisujeme jako O(N) a říkáme, že je to vzhledem k N lineární časová složitost.
To je značná nevýhoda oproti struktuře, kterou si ukážeme za chvíli. Určitě ale pole nezavrhujme. Je to základní datová struktura, která nalezne použití ve spoustě programů, a jak si ve druhé části kuchařky ukážeme, můžeme ho použít třeba k rychlému hledání hodnoty metodou binárního vyhledávání. Nyní ale již slibovaná další datová struktura.
Spojový seznam a ukazatele
Pole jsme měli v paměti určené jenom tím, že počítač věděl, kde je jeho začátek a kolik místa v paměti zabírají jeho prvky. Při dotazování na konkrétní index pak podle indexu a podle velikosti prvků počítač přesně věděl, kam do paměti se má podívat, aby našel námi požadovaný prvek (to vše zvládl v konstantním čase). Jednotlivé prvky si tedy vůbec nemusely pamatovat, kde se nachází jejich sousedi, protože všechny prvky seděly v paměti za sebou.
Představme si ale teď situaci, kdy by si každý prvek ještě pamatoval pozice sousedů. Pak bychom mohli mít prvky libovolně rozházené v paměti a jen by se na sebe vzájemně odkazovaly (první prvek by tvrdil, že druhý je na pozici X, druhý by tvrdil, že třetí je na pozici Y, a tak dále).

K lepšímu pochopení tohoto principu je důležité si vysvětlit, co to je ukazatel (nebo také odkaz či anglicky pointer). Každé místo v paměti počítače má své číselné označení, kterému říkáme adresa. Když si vytváříme nějakou pojmenovanou proměnnou, ta se vlastně odkazuje na určité místo v paměti a na tomto místě v paměti je její hodnota.
Co kdyby ale hodnota proměnné byla adresa nějakého jiného místa v paměti? Pak takové proměnné říkáme pointer a umožňuje nám vytvářet výše popsanou strukturu rozházených prvků v paměti.
Spojový seznam je tedy určený svým prvním prvkem (máme v jedné proměnné pointer na tento prvek, který se často nazývá kořen, protože z něj „vyrůstá“ zbytek struktury) a poté u každého dalšího prvku máme za sebou uloženou hodnotu tohoto prvku a odkaz (pointer) na další prvek. Odkazy mezi prvky mohou být i obousměrné, mohou vést dokola (poslední ukazuje na první) či mohou dokonce tvořit nějakou složitější strukturu (pak to ale již nebude čistý spojový seznam).
Pokud pointer nemá nikam ukazovat, realizuje se to odkázáním tohoto pointeru na
adresu NULL. To skoro doslovně říká „Neukazuji nikam“.

Co nám takto vystavěná struktura umožňuje v porovnání s polem? Přístup na konkrétní prvek v ní stojí lineárně času, protože ho musíme „odkrokovat“ od prvního prvku (na který máme pointer), tedy musíme udělat až O(N) kroků. Pokud bychom však pointer na daný prvek už nějak měli, samozřejmě na něj můžeme přistoupit v konstantním čase.
Naopak přidávání prvků na konkrétní místo (i jejich odebírání) máme v podstatě zadarmo a spojový seznam můžeme rozšiřovat, dokud na něj máme v počítači paměť. Ve chvíli, kdy chceme přidat nový prvek za prvek, na který máme pointer, jen šikovně přepojíme ukazatele. Pokud předtím ukazatele vedly A→B, teď povedou A →C →B (a při odebírání naopak).
#include <stdio.h>
#include <stdlib.h>
// Příkazy výše načetly do programu
// standardní knihovny a funkce z nich.
// Struktura pro prvek obsahující dopředné
// i zpětné odkazy. Zkráceně tomuto typu
// budeme říkat "tprvek".
typedef struct prvek tprvek;
struct prvek {
int hodnota;
tprvek *dalsi;
tprvek *predchozi;
};
// Vytvoří nový prvek:
tprvek *novy(int i) {
tprvek *aktualni =
malloc(sizeof(tprvek));
aktualni->dalsi = NULL;
aktualni->predchozi = NULL;
aktualni->hodnota = i;
return aktualni;
}
// Odstraní prvek a vrátí pointer na další
// prvek (vrácení pointeru se hodí při
// odstraňování kořene):
tprvek *odstran(tprvek *aktualni) {
if (aktualni->predchozi != NULL)
aktualni->predchozi->dalsi =
aktualni->dalsi;
if (aktualni->dalsi != NULL)
aktualni->dalsi->predchozi =
aktualni->predchozi;
tprvek *pomocna = aktualni->dalsi;
free(aktualni);
return pomocna;
}
// Vloží a vrátí pointer na nový prvek:
tprvek *vloz_za(tprvek *aktualni, int i) {
tprvek *pomocna = aktualni->dalsi;
aktualni->dalsi = novy(i);
if (pomocna != NULL)
pomocna->predchozi = aktualni->dalsi;
aktualni->dalsi->dalsi = pomocna;
return aktualni->dalsi;
}
// Použití:
int main(void) {
tprvek *koren = novy(1);
tprvek *aktualni = vloz_za(koren, 2);
aktualni = koren;
while (aktualni != NULL) {
printf("%d\n", aktualni->hodnota);
aktualni = aktualni->dalsi;
}
return 0;
}
collections):
class Prvek:
def __init__(self, hodnota):
self.hodnota = hodnota
self.dalsi = None
self.predchozi = None
class Spojak:
def __init__(self):
self.koren = None
def vypis(self, aktualni):
if aktualni is not None:
print(aktualni.hodnota)
self.vypis(aktualni.dalsi)
def vloz_po(self, prvek, za_prvek = None):
if za_prvek is not None:
prvek.dalsi = za_prvek.dalsi
prvek.predchozi = za_prvek
za_prvek.dalsi = prvek
if prvek.dalsi is not None:
prvek.dalsi.predchozi = prvek
if self.koren is None:
self.koren = prvek
def odstran(self, prvek):
if prvek.predchozi is not None:
prvek.predchozi.dalsi = \
prvek.dalsi
if prvek.dalsi is not None:
prvek.dalsi.predchozi = \
prvek.predchozi
# Použití:
prvekA = Prvek("A")
prvekB = Prvek("B")
prvekC = Prvek("C")
prvekD = Prvek("D")
seznam = Spojak()
seznam.vloz_po(prvekB)
seznam.vloz_po(prvekD, prvekB)
seznam.vloz_po(prvekC, prvekD)
seznam.vloz_po(prvekA, prvekC)
seznam.odstran(prvekC)
seznam.vypis(seznam.koren)
Fronta a zásobník
S použitím spojových seznamů (nebo v jednodušším případě dokonce i polí) můžeme zkonstruovat dvě velmi užitečné datové struktury, frontu a zásobník.
Fronta funguje tak, jak si ji asi každý z nás představuje: ten, kdo se do fronty postaví první, také první přijde na řadu. Trochu jinak si ji můžeme představit jako trubku, do které na jedné straně sypeme nějaké věci a na druhé je odebíráme. Anglicky je též nazývaná FIFO („First In, First Out“).
Praktickou realizaci uděláme jednoduše spojovým seznamem. Budeme si držet dva ukazatele, jeden na začátek seznamu, druhý na konec. Když se objeví nový prvek, který do fronty budeme chtít vložit, přidáme ho na konec, zatímco při odebírání z fronty využijeme druhého ukazatele a vezmeme prvek ze začátku.
Druhou velmi podobnou datovou strukturou je zásobník. Jak už ale plyne z anglického názvu LIFO („Last In, First Out“), funguje spíše jako plný šuplík: Nahoru do něj přidáváme nové prvky, a když chceme nějaký odebrat, vezmeme také zvrchu. To znamená, že první se na řadu dostane naposledy vložený prvek.
Implementace je velmi obdobná jako u fronty, jen bude ukazatel pouze jeden a bude ukazovat jenom na jeden konec spojového seznamu, konkrétně na poslední prvek.
Knihovny
Tyto základní struktury už jsou často předpřipravené jako součást určitých knihoven v daném jazyce. Knihovna je většinou sbírka nějakých navzájem souvisejících funkcí, které již někdo sepsal a které si můžeme do našeho programu načíst a používat. Ukázku načtení knihoven můžete vidět například ve výše zmíněném kódu v jazyce C.
Je ale velmi důležité rozumět tomu, jak knihovní funkce vnitřně fungují. Protože jedině když budeme vědět, co je jak rychlé a efektivní, budeme schopni psát rychlé programy.
Teď již víme, jak reprezentovat nejzákladnější datové struktury v počítači, ale mohlo by se nám hodit zastavit se ještě chvíli u dalších struktur. Tentokrát je už budeme studovat trochu teoretičtěji.
Stromy a grafy v informatice
Grafy
S nějakými grafy jste se již možná potkali, ale tento pojem je bohužel docela přetěžovaný. Jedním jeho významem jsou „koláčové grafy“ a jiné další diagramy znázorňující nějaký poměr (ať už to jsou výsledky voleb, nebo poměr lidí, kteří sledovali v televizi Večerníček).
Další význam můžeme nalézt v analytické matematice, kde se potkáme s grafy průběhu nějakých funkcí. My však nemáme na mysli ani jedno z výše zmíněných, teď se budeme bavit o kombinatorických grafech.
Grafem tedy máme na mysli nějakou množinu objektů, říkejme jim vrcholy, a nějaké vztahy mezi nimi. Tyto vztahy nazýváme hranami a jsou vyjádřené dvojicemi vrcholů, mezi kterými vedou. Ukázku takového grafu vidíme třeba na následujícím obrázku.
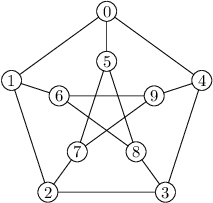
Jako praktickou ukázku grafu si můžeme například představit silniční síť nějakého státu: vrcholy budou města a hrany budou silnice, které mezi nimi vedou.
Občas se můžete setkat s pojmem souvislý graf. Ten znamená jen to, že mezi každými dvěma vrcholy existuje nějaká cesta. Pokud tomu tak není, je graf nesouvislý a dá se rozložit na několik menších grafů, které již souvislé jsou a říká se jim komponenty souvislosti.
Samotný graf poté můžeme doplnit tím, že si v každém vrcholu nebo na každé hraně budeme pamatovat nějakou hodnotu (například cenu nejlevnějšího benzínu ve městech a délku v kilometrech na silnicích). Pamatování si hodnot ve vrcholech je docela obvyklá technika a nemá speciální název, ale pokud budeme mít graf, který si pamatuje hodnoty na hranách, budeme o něm mluvit jako o ohodnoceném grafu.
Další možnou úpravou je, že každá hrana povede jen jedním směrem (jednosměrné silnice), takovým grafům říkáme orientované (pokud pak v orientovaném grafu chceme silnici oběma směry, prostě do něj přidáme dvě hrany, jednu v každém směru).
Poslední, co nám schází k praktickému použití grafů, je naučit se, jak je reprezentovat v počítači. Existuje několik možností (v popisech bude n značit počet vrcholů, m počet hran):
- Seznam sousedů – vrcholy grafu budeme mít uložené v poli a u každého vrcholu budeme mít (spojový) seznam čísel dalších vrcholů, do kterých z aktuálního vrcholu vede hrana. Zabírá místo O(n+m) a hodí se pro řídké grafy (tedy grafy, kde je m řádově stejné jako n).
- Matice sousednosti – tabulka n×n, kde na souřadnicích [i,j] je jednička (nebo jiná hodnota, v případě ohodnoceného grafu), pokud z i do j vede hrana, a nula, pokud tam hrana není (u neorientovaných grafů je navíc matice symetrická – je jedno, jestli vezmeme [i,j] nebo [j,i]). Hodí se pro husté grafy, kde m~n2.
- Matice incidence – řádky reprezentují vrcholy, sloupce hrany. V každém sloupci jsou právě dvě jedničky – indexy vrcholů, mezi kterými hrana vede. Zabírá však O(mn) a její použití bývá dost neohrabané, takže je většinou lepší dát přednost jiné reprezentaci grafu. Je ale dobré o ní vědět.
Grafy jsou velmi široké téma. Můžeme hledat jejich minimální kostry, můžeme v nich hledat nejkratší cesty či skrze ně pouštět pod tlakem vodu. Více o nich si tedy můžete přečíst v některé z našich specializovaných grafových kuchařek, které odkazujeme z našeho kuchařkového rozcestníku.
Stromy
Možná si říkáte, co má informatika u všech elektronů společného s lesnictvím? Kupodivu celkem mnoho a bez stromů bychom se v leckterém případě jen těžko obešli. Informatické stromy sice nejsou většinou tak zelené, mají ale, na rozdíl od svých dřevnatých sourozenců, mnoho jiných pěkných vlastností.
Strom je vlastně speciálním případem souvislého grafu, který neobsahuje žádnou kružnici (cyklus). To znamená, že mezi každými dvěma vrcholy stromu existuje právě jedna cesta.
Díky této vlastnosti můžeme nějaký zvolený vrchol prohlásit za kořen a strom za něj pomyslně zavěsit (tak, že strom roste od kořene směrem dolů), této operaci se říká zakořenění. Pak můžeme mluvit o tom, že z kořene směrem dolů (informatické stromy mají tradičně kořen nahoře) vyrůstají nějaké podstromy.
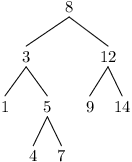
Pokud je strom zakořeněný, můžeme v něm mluvit o hloubce každého vrcholu, neboli o jeho vzdálenosti od kořene. Hloubka celého stromu je pak nejdelší ze vzdáleností od kořene k nějakému z listů (tak říkáme vrcholům, které již nemají žádné syny, tedy vrcholy, které by z nich vyrůstaly). Podle hloubky poté můžeme vrcholy stromu uspořádat do jednotlivých hladin.
Velmi často používáme stromy, které jsou nějak pravidelné. Příkladem jsou třeba binární stromy, které mají v každém vrcholu maximálně dva syny (říkáme jim levý a pravý podstrom). Reprezentovat se dají buď obecně jako každý jiný strom (v každém vrcholu spojový seznam podstromů), nebo velmi pěkně i v poli.
Stačí si pomyslně doplnit binární strom na úplný (to je takový, který má všechny své hladiny plné) a pak ho od kořene směrem dolů po hladinách očíslovat (kořen dostane číslo nula, jeho synové čísla jedna a dva, další hladina čísla tři až šest, atd.).
Můžeme si všimnout, že pokud si v takovém očíslování vezmeme jakýkoliv vrchol s číslem (indexem) i, jeho synové jsou právě vrcholy s indexy 2i+1 a 2i+2. Do pole níže je zapsaný binární strom z obrázku výše.
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| hodnota | 8 | 3 | 12 | 1 | 5 | 9 | 14 | - | - | 4 | 7 |
Jak plyne z očíslování, pro úplný binární strom je uložení v poli efektivní a neplýtváme místem. Pokud ale strom úplný nebude, zůstanou nám v poli volná místa. Uložení v poli se tedy vyplatí jen pro stromy, které se od úplných příliš neliší.
Speciálním případem binárních stromů jsou pak ještě binární vyhledávací stromy. Jsou to normální binární stromy, pro něž navíc platí, že ať si vezmeme libovolný vrchol, budou hodnoty vrcholů v jeho levém podstromu menší než hodnota tohoto vrcholu a hodnoty v jeho pravém podstromu naopak větší.
V takovém stromu pak zvládneme snadno vyhledávat. Budeme ho postupně procházet od kořene a v jednotlivých vrcholech budeme porovnávat hledanou a aktuální hodnotu a podle toho sestupovat do správného podstromu. Podobná technika je detailněji popsaná ve druhé části kuchařky, v sekci Rozděl a panuj.
Na složitější datové struktury stavějící na těchto základních (haldy, intervalové stromy, …) se můžete podívat do některé z našich dalších kuchařek, na jejichž přehled jsme vás už odkázali o kapitolu výše.
Část druhá: Programátorské techniky
Tato část by měla sloužit jako rychlý přehled a ukázka různých technik, které se dají použít při řešení úloh z KSPčka, nebo při programování obecně.

Rekurze
Rekurze je velmi důležitá programátorská technika. V podstatě znamená definování nějaké věci (ať už je to nějaký objekt či postup výpočtu) pomocí sebe sama.
Rekurzivně může být například zadána nějaká datová struktura. Třeba stromy jsou pěkným příkladem rekurzivně definované datové struktury – každý vrchol stromu může mít syny, a každý z těchto synů je sám o sobě strom (tedy i osamocený vrchol bez synů je stromem).
Prakticky je to realizováno tak, že každý vrchol má svou hodnotu a pak ještě seznam ukazatelů vedoucích na další případné podstromy. S ukazateli jsme se již potkali a s jejich pomocí jsme si postavili spojový seznam. A přesně tak, spojový seznam je také ve své podstatě rekurzivní datová struktura.
Kromě rekurzivních datových struktur se ale často potkáváme i s rekurzivním postupem výpočtu nějakého programu, nejčastěji realizovaným ve formě funkce, která volá sama sebe (většinou s jinými parametry, jinak by to asi nemělo smysl), takové funkci se říká rekurzivní funkce.
U rekurzivních funkcí je nejdůležitější věc definovat nějakou koncovou podmínku, tedy podmínku, při níž už se rekurze zastaví. Jinak by se totiž mohlo stát, že by rekurze běžela donekonečna.
Přesněji rekurze by se i tak v nějakou chvíli zastavila, ale skončila by chybou, protože by jí došla paměť – každé volání funkce si totiž ukousne kus paměti (musí si pamatovat, kam se po skončení má vrátit), a pokud má rekurzivní funkce ještě nějaké lokální proměnné, musíme si někde uložit všechny lokální proměnné funkcí, z kterých jsme se doposud nevrátili.
Rekurzivní funkce a převod na nerekurzivní cyklus
Typickým příkladem rekurzivní funkce je výpočet Fibonacciho čísel. Ta jsou definována tak, že f0=1, f1=1 a n-té Fibonacciho číslo je součtem dvou předchozích (fn=fn-1+fn-2). To nám dává posloupnost čísel 0, 1, 1, 2, 3, 5, 8, 13, … pokračující donekonečna. Pokud toto přepíšeme do programového kódu, tak dostáváme následující zápisy:
int fib(int n) {
if (n==0) return 0;
else if (n==1) return 1;
else return fib(n-1) + fib(n-2);
}
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
Jak vidíme, je přepis celkem přímočarý. Pokud by se nám však rekurze v nějakém případě nelíbila, můžeme se každé rekurze zbavit. Rekurzivní volání totiž můžeme šikovně přepsat na nějaký cyklus se zásobníkem.
Pak jen v cyklu odebíráme prvky ze zásobníku, dokud není prázdný, a za každé rekurzivní zavolání do zásobníku přidáme parametry, se kterými bychom naši funkci volali. Tímto postupem převedeme každou rekurzivní funkci na nerekurzivní.
Ještě doplníme poznámku, že ve většině programovacích jazyků každé volání funkce stojí nějaký čas, sice malý, ale když se volání provádí opakovaně, tak se to už nasčítá. Pro reálnou implementaci je tedy nejlepší pokusit se rekurzi převést na nerekurzivní volání, pokud to nějak rozumně jde.
Občas to jde dokonce i jednodušeji a bez zásobníku. Podívejte se na alternativní variantu výpočtu Fibonacciho čísel níže a rozmyslete si, co dělá.
int fib2(int n) {
if (n == 0) return 0;
int a = 0; int b = 1;
while (n > 1) {
int pomocna = a + b;
a = b;
b = pomocna;
n--;
}
return b;
}
def fib2(n):
if n == 0:
return 0
a = 0; b = 1
while n > 1:
(a, b) = (b, a+b)
n -= 1
return b
Jak vidíte, je i tato funkce elegantní a navíc běhá mnohem rychleji než její rekurzivní varianta. Tato funkce běhá v O(n), kdežto rekurzivní varianta počítala stejné věci mnohokrát dokola (zkuste si nakreslit nějaký strom volání předchozí funkce, případně se podívat dopředu do podkapitolky Předpočítané mezivýsledky).
Rekurzivní varianta v tomto případě může běžet až v čase O(2n), což je pro velká n mnohem pomaleji než O(n). Dá se ale celkem lehce rozmyslet úprava rekurzivní varianty, aby běžele také v O(n), zkuste si rozmyslet jak.
Backtracking
S rekurzí silně souvisí i pojem backtracking, česky by se snad dalo říci „metoda pokusu a omylu“. Tímto pojmem označujeme proces, kdy postupně zkoušíme všechny možnosti, jak vyřešit nějaký problém.
Metoda pokusu a omylu se tento proces nazývá proto, že pokud již nemůžeme pokračovat dál (třeba v případě, že v bludišti dojdeme do slepé uličky), vrátíme se kus zpět a zkusíme jinou (zatím nevyzkoušenou) možnost. Takto postupně zkusíme každou možnost, a buď nalezneme námi hledané řešení, nebo se vrátíme až na výchozí pozici a zjistíme, že řešení neexistuje.
Backtracking bývá často realizován pomocí rekurze, ukážeme si to na příkladu hledání rozkladu zadané částky na mince o hodnotách 5 Kč a 3 Kč (všimněte si, že v takto omezeném peněžním systému nejde složit třeba částka 7 Kč). Naše funkce dostane jako parametr zbývající částku a zkusí rekurzivně provést rozklad na jednotlivé mince:
bool rozloz(int castka) {
// Koncová podmínka rekurze
if (castka == 0) return true;
else if (castka < 0) return false;
else if (rozloz(castka-5)) {
printf(" 5 Kc");
return true;
} else if (rozloz(castka-3)) {
printf(" 3 Kc");
return true;
} else return false;
}
def rozloz(castka):
if castka == 0:
return True
elif castka < 0:
return False
elif rozloz(castka-5):
print(" 5 Kc")
return True
elif rozloz(castka-3):
print(" 3 Kc")
return True
else:
return False
V každém kroku zkusíme nejdříve použít pětikorunovou minci a zavoláme se na zbylou částku, a když náš rozklad nevyjde, zkusíme v tomto kroku použít ještě tříkorunu. Takto se rozhodujeme v každém kroku rekurze a případně se vracíme z neúspěšných větví výpočtu a zkoušíme další možnosti.
Takovým postupem ale vyzkoušíme až exponenciálně mnoho možností (O(2n)), což není moc rychlé. Proto je doporučováno se backtrackování raději vyhnout, nebo ho nějak chytře vylepšit. Je však dobré o backtrackování vědět, protože existují problémy, které efektivněji řešit neumíme.
Rozděl a panuj
Jednou ze základních technik je rozdělení složitějšího problému na menší části, které opět můžeme rozdělit na menší a tak dále, dokud se nedostaneme k problémům tak malým, že je už umíme triviálně vyřešit.
Binární vyhledávání v poli
Představme si, že máme seřazené pole n prvků a chceme zjistit, jestli se v něm nachází prvek s hodnotou k. Určitě můžeme projít celé pole v lineárním čase (tím, že budeme brát jeden prvek za druhým a kontrolovat, zda je roven hodnotě k), ale to je zbytečně pomalé a nevyužívá toho, že máme pole seřazené.
Můžeme totiž začít s velkým problémem a ten postupně zmenšovat na stále menší a menší. Nejdříve hledáme k v celém poli. Podíváme se na jeho prostřední prvek:
- Pokud je roven k, jsme hotovi.
- Je-li větší než k, víme, že se k musí nacházet nalevo od něj. Můžeme tedy hledat znovu, ale tentokrát se omezit jen na levou polovinu pole.
- Analogicky, je-li menší než k, můžeme hledat jen v pravé polovině.
Když tímto postupným dělením problémů na menší dojdeme až k poli o velikosti jednoho prvku, stačí tento prvek jenom porovnat, dál už se pole nepokoušíme rozdělovat.
Jelikož se nám každým krokem problém zmenší na polovinu, maximálně po log n krocích se dostaneme na pole velikosti jedna. Říkáme, že algoritmus má logaritmickou časovou složitost, píšeme O(log n). (Pokud není řečeno jinak, znamená pro nás v informatice značka log dvojkový logaritmus, což je funkce opačná k funkci 2n a roste o hodně pomaleji než funkce lineární. Pro velká n platí: 1 < log n < n a například log 2 = 1, log 8 = 3, log 1024 = 10.)
Prakticky postup provádíme tak, že si udržujeme levý a pravý okraj aktuálně zpracovávaného úseku a postupně je k sobě přibližujeme.
int pole[] = {1,2,5,7,12,16,42};
int hledane = 8;
int L = 0, R = 6;
int x;
do {
int prostredni = (L+R)/2;
x = pole[prostredni];
if (x == hledane)
printf("Pole obsahuje hledane\n");
else if (x < hledane)
L = prostredni + 1;
else
R = prostredni;
} while (L < R && x != hledane);
if (x != hledane)
printf("Hledane neni v poli\n");
def bin_vyhled(pole, hledane,
levy_index=0, pravy_index=None):
if pravy_index is None:
pravy_index = len(pole)
while levy_index < pravy_index:
prostredni = (levy_index +
pravy_index) // 2
x = pole[prostredni]
if x < hledane:
levy_index = prostredni + 1
elif x > hledane:
pravy_index = prostredni
else:
return prostredni
return -1
# Zavolání:
print(bin_vyhled([1,2,5,7, 8,12,16,42], 1))
Další aplikace
Další typickou aplikací postupu rozděl a panuj je například třídění posloupnosti pomocí Mergesortu. Ten v základu funguje tak, že každou posloupnost, kterou dostane k setřídění, rozdělí na poloviny a každou z nich setřídí rekurzivním zavoláním sebe sama. Zanořování se zastaví ve chvíli, kdy třídíme posloupnost délky jedna (ta už je z podstaty setříděná). Pak jen v každém kroku ze dvou setříděných menších posloupností vyrobí jejich sléváním setříděnou posloupnost dvojnásobné délky.
Více se o metodě Rozděl a panuj můžete dozvědět ve stejnojmenné kuchařce.
Předpočítané mezivýsledky
Motivací k této kapitole je následující motto: „Proč počítat něco vícekrát, když nám to stačí spočítat jednou a zapamatovat si to?“.
Velmi často se totiž setkáváme s tím, že něco počítáme stále dokola. Jako příklad si můžeme připomenout naši rekurzivní implementaci počítání Fibonacciho čísel zmíněnou výše.
Když se podíváme na výpočet čísla fib(5), vidíme, že pro něj voláme fib(4)
a fib(3), fib(4) volá fib(3) a fib(2), fib(3) volá
fib(2) a fib(1) a tak dále. Všimli jste si, kolikrát se nám tyhle
výpočty opakují? Některá Fibonacciho čísla spočteme totiž zbytečně mnohokrát.
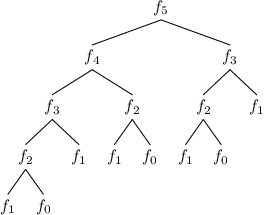
Kdybychom si je namísto opakovaného počítání někde pamatovali, mohli bychom pak odpověď na dotaz na již vypočtené číslo vytáhnout jako králíka z klobouku v konstantním čase. Zavedením jednoho globálního pole, ve kterém si tyto hodnoty pro jednotlivá n budeme pamatovat, nám sníží časovou složitost z O(2n) na pěkných O(n). Takovému postupu se obecně říká dynamické programování.
Dynamické programování

Nejprve uveďme na pravou váhu výraz „dynamické“ v názvu. Nevystihuje tak úplně podstatu této techniky a jeho historické pozadí je celkem složité, avšak dnes je tento název již tak zažitý, že se už pravděpodobně nezmění.
Slovo „dynamické“ částečně odkazuje na to, že se dynamicky (za běhu programu) postupně staví řešení jednodušších problémů, která jsou následně použita pro řešení složitějších. Jeho hlavní podstatou je tedy ukládání a opětovné použití již jednou vypočtených údajů.
Hodí se na úlohy, které se dají dělit na podúlohy, které jsou si podobné a mohou se opakovat. Výsledky takovýchto podúloh si poté ukládáme a při dotazu na stejnou podúlohu vrátíme jen uložený výsledek a výpočet již neprovádíme.
Pro další prohloubení znalostí můžete na našem webu nahlédnout do další kuchařky, tentokrát nesoucí (překvapivě) název Dynamické programování.
Prefixové součty
Velmi často se nám hodí si ještě před samotným výpočtem předpočítat a uložit nějaké hodnoty, které poté použijeme.
Představme si například problém nalezení souvislého úseku s největším součtem v nějaké posloupnosti kladných i záporných čísel. Že to není úplně jednoduchý příklad, si ukažme na následující posloupnosti:
Máme zde dvě ryze kladné souvislé posloupnosti, každou se součtem 9 (4,5 a 2,7). Ale přesto je výhodnější vzít i nějaké záporné hodnoty a vytvořit tak souvislou posloupnost o součtu 12 (zkuste ji nalézt).
Mohlo by nás napadnout, že prostě zkusíme vzít všechny možné začátky a všechny možné konce. To nám dává O(n2) možných posloupností (máme n možných začátků a ke každému z nich řádově n možných konců), pro každou posloupnost si spočteme součet (to zvládneme v O(n)) a budeme si pamatovat ten největší nalezený. Celý náš postup tak trvá O(n3).
To není pro takhle jednoduchou úlohu zrovna ten nejpěknější čas, zkusme ho zlepšit. Ukážeme si, jak vypočítat součet libovolné posloupnosti v konstantním čase. Celý princip je vlastně až kouzelně jednoduchý, ale zároveň velmi mocný. Na začátku výpočtu si do pomocného pole P stejné délky jako posloupnost na vstupu (té říkejme S) uložíme takzvané prefixové součty: i-tý prefixový součet je součet prvních i+1 prvků S, neboli P[i] = S[0] + S[1] + … + S[i].
Pro náš ukázkový případ a pro vstupní pole označené S by to dopadlo takto:
| i | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| S[i] | 1 | -2 | 4 | 5 | -1 | -5 | 2 | 7 | |
| P[i] | 0 | 1 | -1 | 3 | 8 | 7 | 2 | 4 | 11 |
Pole prefixových součtů umíme získat v linerárním čase – prostě jen od začátku procházíme vstupní pole, počítáme si průběžný součet a ten zapisujeme.
Součet libovolného úseku a…b pak získáme v konstantním čase jako prefixový součet od začátku do indexu b minus prefixový součet od začátku do indexu a. Zapsáno programově to pak je:
soucet = P[b] - P[a-1];
To nám umožňuje snížit čas potřebný na řešení této úlohy na O(n2). To je už
lepší čas; prozradíme však, že tuto úlohu lze řešit dokonce v lineárním čase,
ale to je již nad rámec této kuchařky.
Dvourozměrné prefixové součty
Prefixové součty se dají zobecnit i do více rozměrů, ale princip je vždy stejný. Například dvourozměrné prefixové součty u matice fungují tak, že si předpočítáme součty podmatic začínajících levým vrchním políčkem a končící na indexu [x,y].
Z toho je vidět, že prefixový součet zpravidla obsadí stejně velký prostor jako původní data, v tomto případě tedy budeme mít matici hodnot prefixových součtů končících na zadaných souřadnicích. Jak ale získat součet nějaké podmatice, která se nachází někde „uprostřed“ naší matice?
Použijeme stejný princip jako u jednorozměrného případu: Přičteme větší část, kterou chceme započítat, a odečteme od ní části, které započítat nechceme. Pro případ podmatice začínající vlevo nahoře na pozici [x,y] a končící napravo dole na [X,Y] to ilustruje následující obrázek:
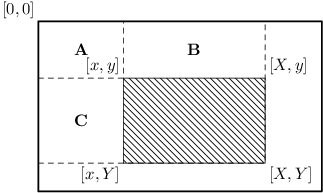
Nejdříve přičteme celý prefixový součet končící na pozici [X,Y]. Tím jsme ale započítali i části A, B a C z obrázku, které započítat nechceme. Tak odečteme prefixové součty končící na indexech [X,y] a [x,Y]. Ale pozor, teď jsme odečetli jednou A+B a jednou A+C, tedy část A (prefixový součet končící na pozici [x,y]) jsme odečetli dvakrát, musíme ji proto ještě jednou přičíst.
Celý vzorec tedy vypadá takto:
soucet = P[X,Y] - P[X,y] - P[x,Y] + P[x,y];
Tento princip přičítání a odečítání se dá zobecnit i pro libovolné vyšší rozměry, ale chce to již trošku představivosti, co se má přičíst a kolikrát. Říká se tomu také princip inkluze a exkluze a najde použití nejen u vícerozměrných prefixových součtů.
Vyvážení délky předvýpočtu a hlavního výpočtu
Správně vyvážit, kolik času můžeme věnovat na předvýpočet a kolik času na hlavní výpočet, je velice důležitá věc a spousta i zkušenějších řešitelů v tom občas chybuje. Přitom to při troše počítání není vůbec nic složitého.
Jako první je potřeba vědět, kolikrát nám předvýpočet během běhu programu pomůže. Předvýpočtem si totiž vybudujeme za nějaký čas určitou datovou strukturu, pomocí které pak dokážeme rychle odpovídat na zadané dotazy.
Označme si počet takovýchto dotazů, které program za běhu dostane, jako Q. Buď to může být hodnota přímo ze zadání typu „Zkonstruujte datovou strukturu pro n hodnot, která zvládne rychle odpovídat na dotazy daného typu, a očekávejte řádově m dotazů“, nebo se může jednat o nějaký interní dotaz v rámci běhu programu (příklad interního dotazu je třeba výše uvedený algoritmus na hledání souvislé podposloupnosti s co největším součtem, který se za běhu ptal na součty nějakých úseků).
Dále si označme jako Op čas, který nám zabere předvýpočet a jako Oq čas, který nám ušetří každý předvypočítaný dotaz. Celkový čas, který ušetříme, je pak vlastně Q · Oq. Pokud je tento čas řádově větší než Op, předvýpočet má smysl.
Naopak nemá smysl trávit předvýpočtem řádově více času, než by trval samotný výpočet bez použití předpočítaných hodnot.
Jako příklad uvažujme problém o velikosti n, u kterého máme tři možnosti, které můžeme zvolit. Můžeme buď předvýpočet úplně vynechat a na každý dotaz odpovídat v čase O(n), nebo provést předvýpočet v čase O(n log n) a poté odpovídat na každý dotaz v čase O(log n), nebo provést předvýpočet v čase O(n2) a pak odpovídat v čase O(1) na dotaz.
Kdy se nám co hodí?
- Pokud bychom dostali jen jeden dotaz, nemá smysl si cokoliv předpočítávat a odpovíme jednou v čase O(n).
- Pokud bude dotazů řádově n, má smysl použít první předvýpočet. Pak budeme mít čas na předvýpočet i na samotný výpočet O(n log n), což je optimum.
- Naopak pokud by dotazů bylo řádově n2 nebo víc, tak se nám již první předvýpočet nevyplatí, dostali bychom se totiž na čas O(n2 log n). Zde se hodí použít druhý, delší předvýpočet a pak se dostat na časovou složitost O(n2 + n2 · 1) = O(n2).
Hladové algoritmy
Věřte nebo ne, ale i počítač se někdy cítí hladový. Po namáhavé práci mu můžeme dopřát to potěšení, aby si ukousl co největší kus dat. A ukážeme, že někdy je to i ku prospěchu. Řeč bude o hladových algoritmech.
Takovými algoritmy rozumíme ty, které hledají řešení celé úlohy po jednotlivých krocích a splňují následující dvě podmínky:
- V každém kroku zvolí lokálně nejlepší řešení.
- Provedené rozhodnutí již nikdy neodvolává (tedy nebacktrackuje).
Lokálně nejlepší řešení je takové, které v aktuálním kroku vybere tu možnost, která nám na tomto místě nejvíce pomůže (bez jakéhokoliv ohledu na globální stav). Může to být třeba nejvyšší hodnota, nebo nejkratší cesta v grafu.
Pokud ale od hladového algoritmu chceme, aby nám našel globálně nejlepší řešení, musí naše úloha splnit předpoklad, že si výběrem lokálně nejlepšího řešení nezhoršíme to globální. Tento předpoklad se nedá formulovat obecně a je nutné se nad ním zamyslet zvlášť u každé úlohy.
Příklady hladových algoritmů
První hladovou úlohou bude (jak jinak) automat na jídlo vracející mince. Automat by měl vracet peníze nazpět tak, aby vrátil daný obnos v co možná nejmenším počtu mincí. Pro náš měnový systém (máme mince hodnot 1, 2, 5, 10, 20 a 50 Kč) lze tuto úlohu řešit hladovým algoritmem – v každém kroku algoritmu vrátíme tu největší minci, kterou můžeme (tedy pro vrácení 42 Kč to bude 42 = 20 + 20 +2 Kč).
Měnové systémy většiny států jsou postavené tak, aby fungovaly takto pěkně, neplatí to ale obecně. Zkusme si vrátit 42 Kč, pokud bychom měli jen mince hodnoty 20, 10 a 4 Kč. Správným řešením je 42 = 20 + 10 + 4 + 4 +4 Kč, hladový algoritmus by ale zkusil vrátit 42 = 20 + 20 + … a tady by selhal.
Dále se velmi často dají hladovým algoritmem řešit nějaké úlohy přidávání nebo odebírání skupin prvků. Typickým příkladem je třeba rozvržení naplánovaných přednášek do učeben. Seřadíme si začátky přednášek podle času a postupně bereme jednu za druhou a umísťujeme je do volných učeben s nejnižším číslem.
Tím jsme si určitě nic nerozbili, protože v nějaké učebně přednáška být musí. Určitě budeme potřebovat tolik učeben, kolik je maximálně přednášek v jeden čas, a díky tomu si umístěním přednášky do nějaké učebny nezablokujeme místo pro jinou přednášku, jelikož nám vždy zbude dostatek volných učeben.
Kdybychom ale naopak měli pevně zadaný počet učeben a chtěli jsme do nich umístit co možná nejvíce přednášek, nejedná se již o úlohu řešitelnou hladovým algoritmem, v takovém případě je potřeba zvolit nějaký chytřejší postup.
Závěr
Doufám, že jste si z tohoto rozsáhlého textu odnesli nějaké nové znalosti a poznatky, které vám pomohou nejen v řešení KSP.
Pokud jste začínajícími řešiteli, zkuste s pomocí kuchařky vyřešit několik lehčích úloh a jejich řešení poslat – nově nabyté znalosti je totiž nejlepší co nejdříve protrénovat. Nic si nedělejte z toho, pokud napoprvé nevyřešíte všechno, s postupným zkoušením se budou vaše znalosti jen zlepšovat. Zkušenější řešitelé možná v kuchařce nalezli nějaké ujasnění pojmů, či si některé techniky osvěžili.
A pokud tento text považujete za dobrý, budeme jen rádi, pokud ho doporučíte svým kamarádům a spolužákům, kteří chtějí s programováním začít.