Pátá série sedmnáctého ročníku KSP
Celý leták v PDF.
- Termín série: 2. květen 2005
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 17-5-1: Velkovezír
- 17-5-2: Ranní hroše
- 17-5-3: Nouze V-Dáli-hrocha
- 17-5-4: Kudy tudy cestička
- 17-5-5: Jazykozpytec se loučí
Milí řešitelé!
Blížící se Velikonoce zaujaly i našeho kamaráda:
Hody hody doprovody, já jsem malý hrošíček,
utíkal jsem podle vody, dohonil mě zajíček.
V košíku však místo vajec úložky měl z Ká eS Pé,
kdo je rychle nevyřeší, ten bude mít u něj zle.
17-5-1 Velkovezír (10 bodů)
Když šel malý hrošík koledovat, srazil se na cestě se zajíčkem. Zajíček, který velmi pečlivě dodržoval velikonoční zvyky, také se mu říkalo Velmi komerční velikonoční zaječí raubíř, mu povídá: „Dávej přece pozor, když jde koledovat ten nejlepší koledník z okolí!“
„Vůbec nejsi nejlepší, Velkovezíre. Já jsem minulý rok vykoledoval čtyřicet dva vajíček!“ „No, to je sice pravda, ale za poslední tři roky jsem jich já vykoledoval sto dvanáct!“ „Ale před pěti lety jsem jich já vykoledoval šedesát čtyři!“
Když ani po notné chvíli nepřestali, rozhodli jste se jim pomoci a spravedlivě určit, který z nich je lepší koledník. Nakonec jste se dohodli, že lepší koledník je ten, jehož průměr vykoledovaných vajíček za souvislé období alespoň K roků je největší.
Napište zvířátkům program, který dostane na vstupu přirozená čísla N a K taková, že 1≤ K≤ N. Dále dostane posloupnost N celých čísel a Vaším cílem je najít takovou souvislou podposloupnost této posloupnosti délky alespoň K, že má největší aritmetický průměr, což je součet jejích prvků vydělený jejich počtem. Pokud je takových podposloupností víc, vypište libovolnou z nich. Ale protože se mezitím hádka přiostřila, měl by Váš program pracovat co nejrychleji.
Příklad: Pro N=5, K=2 a posloupnost (4,8,-2,15,-5) by měl Váš program najít (8,-2,15) s průměrem 7.
17-5-2 Ranní hroše (9 bodů)
Poté, co jste rozhodli při hrošíka s Velkovezírem (bohužel v hrošíkův neprospěch), se malý hrošík vrátil domů a stěžoval si tatínkovi, že Velkovezír je lepší koledník než on. „Tatínku, proč je lepší než já?“ „A kdypak jsi dneska vstával?“ „Časně ráno, sluníčko ještě nezapadlo.“ „A vida ho, našeho lenocha. Nevíš, že ranní hroše dál doduše? Zajíček určitě vstává brzo a každý mu dá spoustu vajíček.“
To malého hrošíka nadchlo. Pokud je to pravda, určitě by dokázal vstát jednou v roce už před polednem. Ale aby zjistil, jestli je to opravdu tak, jak tatínek říká, běžel se zeptat zajíčka, odkdy dokdy chodil o Velikonocích koledovat.
Ale když se vrátil, musel jít špinit nádobí (hroši mají čisté nádobí neradi) a proto Vám dal následující úkol.
Dostanete dvě množiny H a V, každá obsahuje nějaké intervaly tvaru (od,do). Jednotlivé intervaly znamenají odkdy dokdy chodila zvířátka koledovat, v množině H jsou časy hrošíka a v množině V časy Velkovezíra. Máte zjistit, zda hrošík někdy začal a skončil s koledováním dřív než zajíček. Matematicky řečeno zjišťujete, zda existuje nějaký interval h z množiny H a v z množiny V, že h začíná dříve než začíná v a h končí dříve než končí v, čili že hod<vod a hdo < vdo.
Příklad: Pro zadané množiny H={(10,100),(5,200)} a V={(8,110),(20,105)} je hledané h=(10,100) a v=(20,105), protože 10 < 20 a 100<105. Pokud by bylo V={(8,110),(9,105)}, hledané intervaly by neexistovaly.
17-5-3 Nouze V-Dáli-hrocha (8 bodů)
Hrošík teď už věděl, proč je zajíček lepší koledník než on, a rozhodl se, že ho příští rok překoná. Ale aby toho dosáhl, musí si své koledování podrobně naplánovat. Rozhodl se, že bude věren přísloví Nouze naučila V-dáli-hrocha houstnouti, bude jíst jen šestkrát denně, a celý rok plánovat své koledování.
Rád by si vybral nejrychlejší trasu, podél které bude koledovat. A aby byla opravdu nejrychlejší, rozhodl se projít všechny možnosti, které má, a vybrat tu nejlepší.
Hrošík bude koledovat u N svých sousedů. Jeho trasa je vlastně pořadí, v jakém bude své sousedy navštěvovat, takže je to posloupnost čísel 1,2,… ,N, ve které se každé vyskytuje právě jednou. Hrošík by po Vás chtěl, abyste mu vypsali všechny možné trasy, které má, každou právě jednou. Navíc by si ale přál, aby se dvě trasy vypsané hned po sobě lišily jenom prohozením jedné dvojice sousedů (čili aby se posloupnosti reprezentující trasy shodovaly ve všech prvcích kromě dvou, které jsou prohozené). První a poslední vypsané trasy se mohou libovolně lišit.
Bonus: Pokud se bude i první a poslední trasa lišit právě prohozením jedné dvojice prvků, dostanete bonus 3 body.
Příklad: Pro N=3 je jedním ze správných výstupů (i pro bonusovou úlohu):
| 1 | 2 | 3 |
| 2 | 1 | 3 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
| 2 | 3 | 1 |
| 1 | 3 | 2 |
17-5-4 Kudy tudy cestička (11 bodů)
Zatímco si hrošík vybíral nejkratší trasu, uběhl skoro celý rok. A tak den před Velikonocemi hrošík zjistil, že už půjde zítra koledovat, a přitom neví, jakou trasou vlastně půjde.
Protože je hrošík Váš kamarád (nebo snad proto, že nemáte rádi zajíčky?), určitě mu rádi poradíte, tentokrát trochu konkrétněji než v minulé úloze.
Hrošík chce opět navštívit N svých sousedů. Tyto sousedy si můžete představit jako body v rovině. Navíc pokud si všechny tyto body představíte jako vrcholy N-úhelníku, platí, že tento N-úhelník je konvexní (to znamená, že všechny jeho vnitřní úhly mají velikost menší než 180°).
Mezi některými dvojicemi sousedů vedou pěšinky, každá je nějak dlouhá. Všechny pěšinky jsou úsečky, každá spojuje dané dva body odpovídající sousedům, mezi kterými vede. Různé úsečky se samozřejmě mohou křížit.
Hrošík by chtěl takovou trasu, která začíná u libovolného souseda, bude se skládat jenom z daných pěšinek a navštíví každého souseda právě jednou. (To znamená, že na své trase použije právě N-1 pěšinek.) Navíc se žádné dvě pěšinky, které jsou v trase použity, nesmí křížit. A aby mohl být hrošík lepší koledník než Velkovezír, Vámi nalezená trasa by měla být nejkratší možná.
Váš program tedy dostane na vstupu N, dále souřadnice N bodů v rovině, které tvoří konvexní mnohoúhelník, a dále seznam M pěšinek, každá vede mezi jinou dvojicí sousedů a má nějakou délku. Všechny pěšinky jsou obousměrné a jsou to úsečky spojující body odpovídající sousedům, mezi kterými pěšina vede. Vaším úkolem je najít takovou nejkratší trasu, která navštíví každého souseda právě jednou a žádné dvě z pěšinek této trasy se nekříží. Pokud je jich víc, vypište libovolnou z nich.
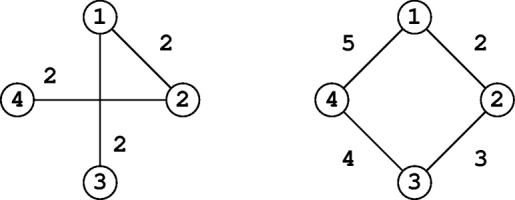
Příklad: Pro 4 body (0,1),(1,0),(0,-1),(-1,0) a pěšinky
| odkud | kam | délka |
| 1 | 2 | 2 |
| 1 | 3 | 2 |
| 2 | 4 | 2 |
žádná hledaná trasa neexistuje. Pro pěšinky
| odkud | kam | délka |
| 1 | 2 | 2 |
| 2 | 3 | 3 |
| 3 | 4 | 4 |
| 4 | 1 | 5 |
hledaná trasa existuje, hrošík navštíví sousedy v pořadí 4,3,2,1.
Pro představu následuje obrázek obou popsaných případů:
17-5-5 Jazykozpytec se loučí (10 bodů)
V posledním díle našeho automatově-gramatického seriálu jsme si slíbili povědět něco o dalších typech gramatik. (Asi se bude hodit připomenout si, co je to gramatika. Přesnou definici, komentáře a příklady čtenář najde v prvním díle seriálu.)
Bezkontextová gramatika je gramatika skládající se pouze z pravidel tvaru
kde
- X∈VN je neterminál,
- α∈(VT∪VN)* je nějaká konečná posloupnost terminálních či neterminálních symbolů.
Jak vidíme, oproti gramatikám popisujícím regulární jazyky (připomeňme, že ty obsahují pouze pravidla X→wY nebo X→w) je pravá strana pravidel poněkud volnější.
Příklad: Jazyk všech palindromů (množinu všech slov, co se čtou pozpátku stejně jako zepředu) nad abecedou {a,b} popisuje následující jednoduchá bezkontextová gramatika (VN, VT, S, P). Jediný neterminální symbol VN={S} je zároveň počáteční, terminální symboly jsou VT={a,b} a přepisovací pravidla P jsou
Například slovo babab dostaneme posloupností přepisů
Pokud vás mate název „bezkontextové gramatiky“, pak vězte, že existují ještě tzv. kontextové gramatiky, které obsahují pouze pravidla tvaru
kde
- X∈VN je neterminál,
- α,β∈(VT∪VN)* jsou libovolné konečné posloupnosti, klidně prázdné, terminálních či neterminálních symbolů,
- γ∈(VT∪VN)+ je libovolná posloupnost terminálních či neterminálních symbolů s výjimkou prázdného slova λ.
Navíc ještě povolíme pravidlo S→λ, pokud se S nevyskytuje na pravé straně žádného pravidla. Ačkoliv na první pohled vypadá docela chaoticky, že jsme zakázali všechna zkracující pravidla a právě toto jedno povolili, vězte, že je to opravdu potřeba, protože jinak by vznikla daleko obecnější třída jazyků, než chceme, nebo by naopak kontextové jazyky nebyly rozšířením bezkontextových nebo regulárních. O podrobnostech pro tentokrát pomlčíme.
Lidsky řečeno, kontextové gramatiky mohou pro rozexpandování symbolu X využít ještě informaci o tom, jakými symboly je právě obalen, tedy v jakém se nachází „kontextu“, a na základě tohoto kontextu provádět odlišné expanze.
Příklad: Ukážeme si gramatiku, která popisuje jazyk L={an bn cn; ∀n∈N, n>0}. Gramatika G=(VN, VT, S, P) bude používat neterminální symboly VN={S,B,C,X}, terminální symboly VT={a,b,c} a množina přepisovacích pravidel P bude následující:
| S | →aSBC | abC …namnož pomocné symboly |
| CB | →BC …setřiď je (Pozor, podvod!) |
| bB | →bb …a zruš všechny pomocné symboly |
| bC | →bc |
| cC | →cc |
Všimněte si řádku, kde upozorňujeme na podvod. Toto pravidlo samozřejmě není kontextové. Namísto něj ve skutečnosti použijeme tři pravidla
| CB | →XB |
| XB | →XC |
| XC | →BC, |
o kterých už každý snadno vidí, že jsou kontextová a dělají to samé, co původní pravidlo. Slovo aabbcc dostaneme například touto posloupností přepisů:
| S→aSBC→aabCBC→aabXBC→aabXCC→ |
| →aabBCC→aabbCC→aabbcC→aabbcc |
S naší sadou pravidel zjevně bude všech symbolů a,b,c stejný počet a navíc jediná možnost, kdy se expandování gramatiky může zastavit, je, když jsou symboly utříděné. Gramatika G je tedy schopná vytvořit libovolné slovo z jazyka L a už nic dalšího navíc.
Soutěžní úloha 1: Sestrojte kontextovou gramatiku, která popisuje jazyk L={ai bj ck; 1≤ i≤ j≤ k}. Například slova aabbcc či abbccc do L patří, slova aaabbc či cba do L nepatří. [5 bodů] Soutěžní úloha 2: Sestrojte kontextovou gramatiku, která popisuje jazyk L={a2n; ∀n∈N}, čili jazyk všech slov ze symbolů a, jejichž počet je mocninou dvojky. Tedy například slova a, aa a aaaa do L patří, avšak slovo aaa do L nepatří. [5 bodů]
Dejte si zejména pozor na to, aby vámi sestrojená gramatika byla skutečně kontextová a nepoužívala nepovolená pravidla. Vaše řešení by měla obsahovat zdůvodnění, že gramatika dělá to, co má, případně důkaz, že hledáme marně a příslušná gramatika neexistuje.
O nedeterministických zásobníkových automatech, kterým byl věnován předchozí díl seriálu, se dá dokázat, že rozpoznávají právě jazyky popsatelné bezkontextovou gramatikou. Důkaz je však poněkud obtížnější a my si ho předvádět nebudeme. Dají se zavést i podstatně mocnější výpočetní prostředky, než jsou zásobníkové automaty, například různé varianty tzv. Turingových strojů. U mnoha z nich se potom ukazuje souvislost s nejrůznějšími typy gramatik. Konkrétně kontextové gramatiky popisují právě jazyky, které jsou rozpoznatelné nedeterministickými Turingovými stroji v paměťovém prostoru omezeném lineárně vzhledem k délce vstupu.
V našem seriálu však již nezbývá dosti časoprostoru na to, abychom si tyto další stroje a gramatiky popsali, natož o nich ukázali něco zajímavého. Ještě bychom však rádi dodali, že teorie formálních jazyků je podkladovou teorií nejdůležitější informatické vědy – teorie složitosti. Rozhodovací algoritmické problémy se totiž dají převést na problém rozpoznávání určitého jazyka. Že se teorie gramatik hodí například při psaní překladačů programovacích jazyků, si čtenář jistě domyslí sám.
Tímto se tedy s vámi loučíme a děkujeme za pozornost, kterou jste formálním jazykům věnovali.