Čtvrtá série začátečnické kategorie třicátého pátého ročníku KSP
Celý leták v PDF.
Řešení úloh
 35-Z4-1 Lampy v ulici (Zadání)
35-Z4-1 Lampy v ulici (Zadání)
Úlohu si nejprve trochu zjednodušíme: lampy, které sousedí s rozbitou lampou, musí určitě svítit, čímž rozdělují ulici na nezávislé části – jak pozhasínáme lampy vlevo od rozbité, neovlivní pozhasínání lamp vpravo od rozbité. Můžeme tedy řešit každý úsek oddělený rozbitou lampou zvlášť.
Lampy na okrajích těchto úseků musí svítit určitě, protože jsou buďto na okraji města, nebo sousedí s rozbitou lampou. Zbylé lampy můžeme „na střídačku“ pozhasínat. Jednu zhasneme, tím pádem další musí svítit, tu za ní tedy můžeme zase zhasnout, atd.
Pokud bude délka úseku lichá, musíme zhasnout hned druhou lampu v úseku, protože jinak by zbyly dvě rozsvícené lampy vedle sebe na začátku a na konci úseku, což je plýtvání:
OO-O-O-OO
je méně efektivní než
O-O-O-O-O.
Pokud je délka úseku naopak sudá, je jedno, jestli dvě rozsvícené budou na začátku, nebo na konci:
OO-O-O-O
vyjde stejně jako
O-O-O-OO.
Z těchto pozorování tedy můžeme odvodit úplně jednoduché pravidlo: Můžeme zhasnout vždy první možnou lampu v každém úseku a pak střídavě zhasínat a nechávat svítit zbytek lamp až do konce úseku.
Když to trochu přeformulujeme, tak již dostaneme výsledný algoritmus. Budeme procházet lampy zleva a kdykoliv má nějaká vedle sebe dvě rozsvícené, tak ji zhasneme a pokračujeme dál. Díky výše popsaným pozorováním si jsme jistí, že takto najdeme nejúspornější rozsvícení pouličního osvětlení.
Protože jednou projdeme všechny lampy, tak je časová složitost algoritmu O(N), kde N je počet lamp v Hrochovníku.
 35-Z4-2 Nudná hodina (Zadání)
35-Z4-2 Nudná hodina (Zadání)
Nejprve uvažme zjevný postup, jak číslo n na prvočísla rozložit. Pro každé
prvočíslo p < n vyzkoušíme, kolikrát lze n vydělit p beze zbytku. Podle
tohoto počtu k pak vypíšeme p, p^k nebo nic.
Na nalezení prvočísel bychom mohli použít například Eratosthenovo síto,
které bychom pustili pouze jednou při startu programu.
Tento postup jistě funguje, je však velmi pomalý. Nejen že potřebujeme najít všechna prvočísla menší než n, ale i v případě, že n je prvočíslo, jej vydělíme každým prvočíslem. Zkusme tedy najít triky, jak zrychlit výpočty.
Nejprve se zbavíme nutnosti najít prvočísla. Postupně zkusíme všechna čísla od 2 do n, ať už jsou prvočísla nebo ne. V průběhu algoritmu budeme používat průběžně se měnící m, které bude reprezentovat tu část čísla, kterou je ještě potřeba rozložit. Na začátku bude m rovno n. Pak, když testujeme číslo p, nastavíme k = 0. Pokud je m dělitelné p, nahradíme jej m/p a k zvýšíme o 1. Jinak (ne)vypíšeme pk jako původně a přesuneme se na další číslo p+1. V případě, že m = 1, můžeme skončit.
Proč toto funguje? Všimněme si, že není-li x dělitelné číslem y, pak není dělitelné ani žádným jeho násobkem. Jak tohle využít pro hledání rozkladu? Uvažme, že n je dělitelné prvočíslem p, ale jeho podíl m = n/p už není. Pak složená čísla dělitelná p taky nebudou dělit m. Naopak, pokud n je dělitelné jiným prvočíslem, bude jím stále dělitelné i m.
Jelikož složená čísla jsou násobky menších prvočísel, v době jejich testu je m již nesoudělné s těmito prvočísly a určitě nebudou m dělit. Vydělit beze zbytku se tedy vždy podaří jen prvočíslům v prvočíselném rozkladu n.
Tento postup je už lepší, ale stále testujeme dělitelnost pro n-2 čísel. Učiňme však další pozorování k dělitelnosti: je-li n dělitelné číslem p, pak také n/p dělí číslo n. V našem algoritmu dříve vyzkoušíme to menší z této dvojice čísel. Navíc, alespoň jedno číslo z dvojice je nejvýše √n.
Z toho vyplývá, že je-li m složené číslo, musí určitě ve svém rozkladu obsahovat p ≤ √m. Pokud tedy při testování dělitelnosti dojdeme na číslo větší než √m a zbylo nám m > 1, musí už m být nutně prvočíslo, které následně vypíšeme do rozkladu. Tudíž nám stačí testovat dělitelnost pro čísla od 2 do √m.
Tím už dostáváme algoritmus, který provede O(√n) testů. Ještě musíme započítat úspěšná dělení, ale protože každým dělením se nám m zmenší na nejvýše polovinu, nemůže jich být více než O(log n) ⊆ O(√n). To je i výsledná složitost algoritmu.
To vypadá jako příjemná složitost, ale pokud jako velikost vstupu uvážíme počet číslic b v desítkovém zápisu n, pak 10b-1 ≤ n ≤ 10b a O(√n) = O(10b/2), což je exponenciální – třeba rozkladu n ≈ 1050 se už nedočkáme. Slíbili jsme však v zadání, že n je dost malé.
 35-Z4-3 Záchrana kachničky (Zadání)
35-Z4-3 Záchrana kachničky (Zadání)
Na úlohu můžeme jít odzadu. Víme, do jaké výšky musí vystoupat voda pod kachničkou – o jedna výše, než se kachnička nachází na začátku. Označme tuto výšku v. Najdeme první sloupec za kachničkou, který sahá alespoň do výšky v, nazvěme jej „břeh“. O něj se voda zarazí a dál nedoteče.
Jako počáteční pozici algoritmu si nastavíme sloupec těsně před „břehem“. Potom postupujeme doleva a každý sloupec doplníme vodou do výšky v. Může se nám ale stát, že narazíme na „útes“, tedy sloupec, který bude ještě vyšší než aktuální v. Aby voda tento „útes“ překonala, musí voda před ním vystoupat alespoň do jeho výšky, proto nastavíme v na výšku „útesu“ a pokračujeme dál, než dojdeme na levý konec rybníka. Nakonec vypíšeme celkové množství vody, které jsme museli dolít.
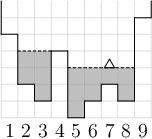
Na obrázku bude „břeh“ představovat sloupec číslo 9, a výška v začne nastavená na 3. První „útes“, na který narazíme, bude sloupec 4, kde se výška nastaví na 4. Jako druhý narazíme na „útes“ ve sloupci 1, kde se výška nastaví na 5.
Algoritmus nejdříve v čase O(N-D) najde „břeh“ a poté v O(N) dolije vodu do jednotlivých sloupců. Paměti spotřebuje O(N) na vstup a O(1) na pomocné proměnné.
 35-Z4-4 Těžba zlata (Zadání)
35-Z4-4 Těžba zlata (Zadání)
Políčka na mapě si rozdělíme do tří kategorií: se zlatem, kamenné bezpečné a kamenné nebezpečné (políčko se šachtou se chová stejně jako kamenné políčko, jen na něm navíc začínáme). Nebezpečná budou kamenná políčka sousedící se zlatem; všechna ostatní kamenná políčka jsou bezpečná. Jako ložisko nazvěme souvislou oblast zlatých políček. Dle zadání bude Zuzka nejprve nějakou dobu kopat jen bezpečná políčka, poté vykope jedno nebezpečné, čímž dostane zlatou horečku, a poté bude kopat už jen políčka se zlatem.
Můžeme nahlédnout, že každé ložisko je „obalené“ nebezpečnými políčky (nebo okrajem mapy), a tedy všechno vykopané zlato musí pocházet z ložiska – resp. nejvýše tří různých ložisek – které jsme odkryli při vstupu na naše první a jediné navštívené nebezpečné políčko. Jiná ložiska bychom totiž museli odkrýt navštívením nějakého dalšího nebezpečného políčka, a to po spatření zlata už nemůžeme.
Optimální řešení tedy vždy musí mít následující tvar: Dojdeme nejkratší cestou po bezpečných políčkách do nějakého nebezpečného políčka a potom vysbíráme všechno zlato, co najdeme. Skvěle, to zní skoro jako algoritmus! Ale do jakého nebezpečného políčka dojít? Vyzkoušíme všechna!
První nástřel našeho řešení funguje přesně takto. Vezme postupně každé políčko a zjistí (z jeho typu a z typu sousedů), zda je kamenné a nebezpečné. Pokud ano, najde k němu nejkratší cestu od šachty po bezpečných políčkách. To lze třeba upraveným prohledáváním do šířky (alias Breadth-First Search neboli BFS), o kterém si můžete přečíst v naší grafové kuchařce: vrcholy jsou políčka, hrany vedou mezi sousedními políčky a navíc algoritmu schováme všechny nebezpečné vrcholy a hrany do nich. BFS nám do každého políčka napíše jeho vzdálenost od šachty, takže pak se stačí podívat na naše nebezpečné políčko a vzít minimum ze vzdáleností jeho bezpečných sousedů zvětšené o jedna. (Může se stát, že žádné bezpečné sousedy nemá, pak se do něj nejde z šachty dostat a můžeme ho přeskočit.)
Podobně můžeme spočítat množství vytěženého zlata: pustíme BFS z nebezpečného políčka, ale tentokrát schováme všechna ne-zlatá políčka a hrany do nich. Pak už stačí z počtu odkrytých zlatých políček a z délky nejkratší cesty do nebezpečného políčka spočítat náš zisk a ten samý algoritmus zopakovat pro všechna nebezpečná políčka a vybrat si to s největším ziskem.
Takové řešení je přímočaré, s mřížkou R × S však pro každé z až RS políček vykonává až Θ(RS) práce, takže jeho časová složitost je Θ(R2S2). Umíme to lépe?
Samozřejmě! Možná jste si všimli, že v první půlce zbytečně počítáme to samé BFS pořád dokola, protože graf i startovní políčko jsou pořád stejné. Spustíme ho tedy jen jednou a předpočítané nejkratší vzdálenosti si zapamatujeme.
S druhou částí už je to horší, tam BFS pokaždé spouštíme z jiného vrcholu. Můžeme však využít pozorování ze začátku řešení: smíme vytěžit jen ložiska, která sousedí s naším nebezpečným políčkem. Kdybychom uměli pro každé zlaté políčko spočítat, do jakého patří ložiska a jakou má toto ložisko velikost, měli bychom vyhráno: pak by stačilo projít všechny (nejvýše čtyři) sousedy našeho nebezpečného políčka, zjistit, zda je v nich zlato a do jakého případně patří ložiska, a posčítat velikosti všech ložisek. Jen pozor, že více sousedů může klidně patřit do toho samého ložiska, my ho však chceme započítat jen jednou.
Přesně to ale umíme! Pokud si mřížku představíme jako graf, kde existují pouze zlatá políčka a hrany mezi nimi, pak se ptáme na rozklad grafu na komponenty souvislosti, který umíme – jak jinak – spočítat (trochu více) upraveným BFS. Algoritmus navíc lze snadno upravit tak, aby kromě příslušnosti políček ke komponentám počítal i velikost komponent. Více opět v grafové kuchařce.
A to je vše. V novém algoritmu na začátku pustíme dvě různá prohledávání nad celou mřížkou, každé se složitostí O(RS). Poté už jen zkoušíme nebezpečná políčka a pro každé provádíme O(1) práce díky předvypočítaným výsledkům, takže celková časová i paměťová složitost našeho algoritmu je taktéž O(RS).
Poznámka na závěr: úloha se ve skutečnosti ptala na optimální pořadí těžení políček, nejen na optimální zisk. V kuchařce popisujeme, jak upravit BFS, aby z něj nejkratší cesta šla také zrekonstruovat. Co ale s druhou částí, rozkladem na komponenty? Asi nejsnazší je nejdříve nechat doběhnout celý náš algoritmus a zjistit, které nebezpečné políčko je nejvýhodnější, a pak výsledek spočítat znova jen s tímto políčkem, ale tentokrát použít pomalejší algoritmus ze začátku řešení. Ten používá BFS i na těžení zlata, takže z něj pořadí políček budeme moct vyčíst celé. Jelikož ho pouštíme jen jednou, nepokazíme si tím časovou složitost.