Třetí série patnáctého ročníku KSP
Řešení úloh
15-3-1 Potrubí (Zadání)
Řešení se k této úloze sešlo poměrně hodně. Většina z Vás ale použila algoritmus, který pro každou hranu (x,y) otestoval, zda se dá z vrcholu x do vrcholu y dostat bez použití této hrany, a pokud ano, tak tuto hranu z grafu vyhodil. Tento algoritmus ale nemusí vždy nalézt správné řešení. Příkladem může být např. úplný orientovaný graf na třech vrcholech.
A jak tedy správně? Podgrafu, který má stejné dosažitelnosti jako původní graf a navíc má minimální počet hran, říkejme MEG (minimální ekvivalentní podgraf). Úlohu si dále rozdělme na několik částí. Nalézt MEG na grafu, který je silně souvislý, tj. z každého vrcholu do každého vede orientovaná cesta, je NP-těžké. Zřejmě bychom tím vyřešili problém Hamiltonovské kružnice. Jednoduše to znamená, že zatím není známo řešení pracující s lepší časovou složitostí než exponenciální. Naopak nalézt MEG na acyklickém grafu je poměrně lehké. Idea řešení je tedy nasnadě. Vstupní graf si rozdělíme na silně souvislé komponenty. Na to existuje klasický Tarjanův algoritmus pracující v čase O(N+M). Naleznete ho ve většině učebnic grafových algoritmů. Faktorgraf podle silně souvislých komponent je zřejmě acyklický (žádné dva vrcholy z různých komponent silné souvislosti neleží na kružnici). Máme-li tedy vrcholy grafu rozděleny do silně souvislých komponent, nalezneme MEG tohoto grafu tak, že použijeme metodu hrubé síly na jednotlivé komponenty, a hrany vedoucí mezi komponentami redukujeme pomocí polynomiálního algoritmu.
Ten pracuje tak, že z každého vrcholu nalezne vrcholy dostupné po orientované cestě, dále nalezne vrcholy dostupné proti orientaci a zruší všechny hrany vedoucí z vrcholů dosažených proti orientaci do vrcholů dosažených po orientaci. To lze jednoduše v čase O(N·(N+M)). Navíc se dá poměrně jednoduše dokázat, že existuje právě jedna minimální redukce acyklického grafu. Viz např. kniha Jiří Demel: Grafy a jejich aplikace, a jiné. Paměťová složitost celého algoritmu je při vhodné implementaci O(N+M).
15-3-2 Permutace (Zadání)
Podívejme se nejdříve, jak bude naše složená permutace Pk vypadat v nějakém konkrétním bodě i pro různá k, tedy vlastně na posloupnost
| p0 | =P0[i]=P[i], |
| p1 | =P1[i]=P[P[i]]=P[p0], |
| p2 | =P2[i]=P[P[P[i]]]=P[p1], |
| . | |
| . | |
| . | |
| pk | =Pk[i]=P[pk-1]. |
Možných hodnot pk je pouze n, takže nejpozději po n krocích se nějaké číslo objeví podruhé, tedy pl=pm pro nějaké 0≤ l < m ≤ n. A jelikož každé číslo závisí pouze na čísle předchozím, začne se od tohoto bodu opakovat celá posloupnost. Snadno také nahlédneme, že číslo, které se nám zopakovalo jako první, musí být první člen posloupnosti – kdyby bylo l>0, stačí se podívat na hodnoty pl-1 a pm-1: buďto jsou stejné, a pak jsme objevili ještě časnější opakování, nebo jsou různé, ale pak nám P zobrazuje dvě různá čísla na jedno, tudíž to není permutace.
Posloupnost složení tedy musí tvořit cyklus délky m, na počest jeho počátečního prvku mu budeme říkat cyklus i-čkový. Navíc tento cyklus můžeme velice jednoduše najít: stačí postupně počítat p0=P[i], p1=P[p0], … a značkovat si, které hodnoty už nastaly. Takto v lineárním čase celý cyklus projdeme a pak už můžeme v konstantním čase spočítat Pk[i] = pk = pk mod m. A když to provedeme pro každé i, získáme řešení naší úložky v čase O(n2).
A to je všechno? Kdepak, jde to lineárně. Stačí k tomu jen málo – uvědomit si, že pro libovolné j ležící na i-čkovém cyklu (tedy j=pz pro nějaké z) je j-čkový cyklus stejný jako i-čkový jen „o z otočený“, takže Pk[j]=Pk+z[i]=pk+z. Náš program si tedy nejdříve permutaci rozloží na cykly (najde první cyklus, pak vezme nejbližší neoznačkovaný prvek a začne od něj hledat další cyklus a tak dále); pro permutaci (2, 1, 4, 5, 3) ze zadání to například dopadne takto:
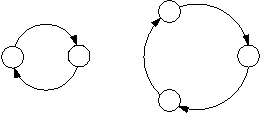
Pak pro každý cyklus projde jeho prvky a spočítá pro ně prvky „o k dál“ na cyklu a ty prohlásí za výsledek (a bude to pravda). To všechno stihne v čase lineárním s délkou cyklu, takže celkem lineárně se součtem délek všech cyklů, což je ovšem přesně n. Paměti stačí také jen O(n).
Aby program (který se podle našeho algoritmu řídí takříkaje do slova a do písmene) nevypadal
tak fádně, napsali jsme ho podle nové normy Céčka zvané C99, posuďte sami, oč se v něm
programuje příjemněji.
15-3-3 Tajemný obraz (Zadání)
Drvivá väčšina riešení načítala vstup do dvojrozmerného poľa, potom troma vnorenými cyklami prešla cez všetky trojice bodiek, zarátala každú trojicu tvoriacu jednofarebný trojuholník. Toto viedlo k algoritmu s kubickou zložitosťou t.j. N3. Za takéto riešenia ste dostali po 5 bodov. Našlo sa jedno exotické riešenie v zložitosti Nlog27.
Hŕstka riešiteľov pochopila, že ten príklad asi taký jednoduchý nebude, a stvorila riešenie s kvadratickou časovou zložitosťou – O(N2) a lineárnou pamäťovou zložitosťou – O(N), podľa ktorého je napísané aj vzorové riešenie. Dostali po 10 bodov.
Jeden bod som stŕhal za chýbajúci alebo zlý odhad časovej alebo pamäťovej zložitosti. Jeden alebo dva body som tiež strhával za chyby v zdrojovom kóde.
A nyní vzorové riešenie: Nebudeme počítať, koľko je na obrázku jednofarebných trojuholníkov, ale naopak, koľko je na obrázku pestrých trojuholníkov t.j. takých trojuholníkov, ktorých strany nie sú rovnakej farby. Ak si označíme počet pestrých trojuholníkov K, tak potom jednofarebných trojuholníkov bude:
| ( | N | ) |
| 3 |
| N(N-1)(N-2) |
| 6 |
Ako ale vypočítať K? Uvážme jednu bodku na obrázku s číslom i. Z nej vychádzajú nejaké modré úsečky a nejaké červené úsečky.
Vezmime nejakú modrú úsečku a nejakú červenú úsečku, obe vychádzajúce z našej bodky. Evidentne naša bodka spolu s koncovými bodmi modrej a červenej úsečky tvoria pestrý trojuholník.
Označme ci počet červených úsečiek vedúcich z našej bodky, potom modrých úsečiek vychádzajúcich z našej bodky bude N-1-ci. Keďže máme na výber z ci červených a nezávisle na tom z N-1-ci modrých úsečiek, takýchto pestrých trojuholníkov tam potom bude ci(N-1-ci).
Spočítajme takéto súčiny pre všetky bodky: P = c1(N-1-c1) + c2(N-1-c2) + … + cN(N-1-cN). Koľkokrát je v súčte P zarátaný nejaký pestrý trojuholník?
| P |
| 2 |
| N(N-1)(N-2) |
| 6 |
| P |
| 2 |
Časová zložitosť je O(M), teda lineárna od počtu červených hrán. Pamäťová zložitosť je lineárna – O(N).
15-3-4 Výsadek (Zadání)
Jak to vlastně dopadlo s vrchním velením krtků? Podařilo se jim vykrtincovat zahradu strýčka Pompa? Ne, všichni by to stihli, rozhodně ne dříve než by si byl strýček koupil nějaký přípravek na hubení krtků, ale našlo se i něco rychlejších řešitelů. Většina z vás řešila problém lineárně, což sice není úplně nejpomalejší, ale protože v zadání byl nabídnut polynomiální čas na předpočítaní, není toto rešení zcela optimalní. Jak tedy řešit? Tento problém šlo řešit v čase O(log n) na dotaz a s časem O(n2) na předpočítání, kde n je velikost vstupu (počet vrcholů n-úhelníka).
Jak pracuje algoritmus na předzpracování? Nejprve si vytvoříme seznam hran na obvodu n-úhelníka. Do seznamu ale nezařazujeme hrany, jejichž koncové body mají stejnou y-ovou souřadnici. Dále setřídíme body podle y-ové souřadnice a ještě se zbavíme vrcholů se stejnou y-ovou souřadnicí (v poli vrcholů máme pouze vrcholy s různými y-vými hodnotami). A nyní si setřídíme hrany tak, aby pokud mají dvě hrany společnou y-ovou souřadnici, tak byly setříděné podle pořadí x-ových souřadnic na společné y-ové souřadnici (protože se hrany nekříží, je tento krok jednoznačný). Pokud hrany společnou y-ovou souřadnici nemají, tak nám na jejich pořadí nezáleží. Rychlé setřídění hran dle těchto pravidel se dá poměrně snadno provést pomocí metody zvané topologické třídění. Výklad této metody si můžete prohlédnout například v úloze 11-1-1. Po setřídění hran si vytvoříme „pásečky“. Ty tvoříme tak, že si v utříděné posloupnosti vrcholů bereme postupně dva následující vrcholy. Ty nám jednoznačně určují páseček v y-ovém směru (díky vyřazení vrcholů se stejnou y-ovou souřadnicí nemáme žádný páseček s nulovou šířkou). Pro každý páseček si vyhradíme pole (případně spojový seznam) a do něho postupně vkládáme hrany, které do něj zasahují (postupně, znamená, že zachovávám jejich uspořádání). A to už je celé předzpracování.
Jak, že to vypadá dotaz? Na vstupu dostaneme bod. Binárním vyhledáním zjistíme v jakém je pásečku. Stejným postupem zjistíme, mezi kterými hranami v pásečku se vyskytuje. A nyní stačí zjistit paritu hrany v seznamu neboli zda je pořadí hrany před vrcholem sudé či liché číslo. Je zřejmé, že vždy při přechodu hrany se musí střídat stav uvnitř a venku zahrady.
Jaká je složitost předzpracování? Na setřídění potřebujeme O(n · log n), ale to zde nehraje roli. Složitost vybrání hran pro pásečky je pro každý páseček O(n) a pásečků je až O(n), a tedy celková složitost předzpracování je O(n2). Složitost dotazu závisí pouze na dvojím binárním vyhledání, které má složitost O(log n).
15-3-5 Haskell (Zadání)
Řešení této úložky je poměrně přímočaré, bez nějakých složitějších myšlenek.
Nejprve je potřeba načíst vstup; to zajišťuje funkce runCgi. Poté musíme
přeskočit daný počet volání cgiPage a nechat následující volání
této funkce vrátit následující dotaz. Toto zajišťuje monáda CGI
ve spolupráci s cgiPage. CGI jen přenáší aktuální stav výpočtu
(funguje na podobném principu jako v zadání popsaná monáda IO) mezi
jednotlivými voláními cgiPage. cgiPage zvýší počítadlo aktuálního
kroku a v případě, že dosáhlo hledané hodnoty, do stavu zapíše zadaný dotaz.
Navíc cgiPage vždy musí vrátit hodnotu, kterou jsme zadali jako odpověď.
Tuto hodnotu najde v tabulce, kterou také přenášíme ve stavu výpočtu (pokud
tato hodnota ještě není známa, vracíme undefined – to nevadí, takovou
hodnotu se nikdo nepokusí vyhodnotit).