Čtvrtá série patnáctého ročníku KSP

Zadání úloh

15-4-1 Archiv (10 bodů)

Pan Sips pracuje jako úředník v archivu, kde se ukládají různé dokumenty. Dokumenty jsou v archivu uloženy vzestupně podle jejich evidenčního čísla. Jednoho dne ale do archivu přišel nový úředník a neznalý zdejšího pořádku uložil některé dokumenty na jiná místa, než kam patří a porušil tím setřídění. Pan Sips je nyní nešťastný, protože setřídit všechny dokumenty je obrovská práce. Požádal vás proto o pomoc s tímto problémem.

Vaším úkolem je napsat program, který na vstupu dostane počet spisů v archívu N a dále posloupnost N evidenčních čísel dokumentů (předpokládejte, že se vejdou do typu long respektive Longint). Na výstup má váš program vypsat setříděnou posloupnost evidenčních čísel. Snažte se, aby třídění proběhlo co nejrychleji, a předpokládejte, že počet špatně zařazených dokumentů je řádově menší než celkový počet dokumentů.

Příklad: Pro posloupnost 1,3,5,2,7,6,10,12,14,11 by váš program měl vypsat posloupnost 1,2,3,5,6,7,10,11,12,14.

Řešení

15-4-2 Permutace podruhé (11 bodů)

Permutace P čísel 1,… ,N je libovolné prosté zobrazení množiny čísel {1,… ,N} na sebe. Permutace tedy přiřazuje každému i∈{1,… ,N} nějaké číslo P[i]∈{1,… ,N} a tato čísla jsou pro různá i různá. Dvojité složení permutace P je permutace P2 definovaná jako:

P2[i] = P[P[i]], ∀i∈{1,… ,N}

Napište program, který dostane na vstupu N a dále N čísel popisujících permutaci P (i-té číslo je hodnota P[i]) a na výstup vypíše počet permutací Q takových, že jejich druhým složením vznikne permutace P (tedy takových, že Q2=P).

Příklad: Permutaci na číslech 1,… ,7 tvaru (2, 1, 5, 6, 7, 4, 3) lze získat jako druhou mocninu dvou permutací – (4, 6, 7, 2, 3, 1, 5) a (6, 4, 7, 1, 3, 2, 5).

Řešení

15-4-3 Koberec (9 bodů)

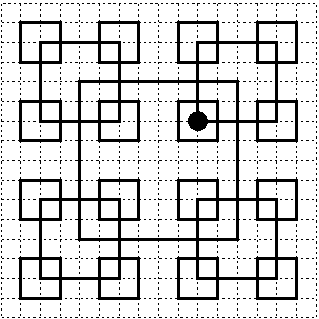
Pan Naisrep tkal v daleké Persii koberce. A nebyly to koberce ledajaké, protože Naisrep se specializoval na čtvercové vzory. Jednoho dne ho napadl následující vzor: Jeho základem byl čtverec se středem uprostřed koberce o straně délky 2k. Ve vrcholech tohoto čtverce ležely středy čtverců o stranách délky 2(k / 2) a ve vrcholech těchto čtverců ležely opět středy menších čtverců a tak dále až dokud čtverce neměly stranu délky 2. Aby vzor nebyl tak jednoduchý, rozhodl se Naisrep jednotlivé oblasti na koberci vyšít různými barvami podle toho, v kolika čtvercích leží. Ale ouha, zjistit, v kolika čtvercích leží nějaké místo, není žádná hračka. A tak se k vám Naisrep obrátil o pomoc.

Vaším úkolem je napsat program, který dostane na vstupu délku strany čtvercového koberce (sudé přirozené číslo, může být i poměrně velké), dále délku strany největšího čtverce (též sudé přirozené číslo) a souřadnice bodu na koberci ([0,0] je levý horní roh). Na výstup má váš program vypsat uvnitř kolika čtverců daný bod leží (pokud bod leží na hraně nějakého čtverce, počítá se, že je uvnitř).

Příklad: Pro koberec o straně délky 16 a největší čtverec o straně délky 8 leží bod se souřadnicemi [6,10] ve třech čtvercích (viz obrázek).

Koberec

Řešení

15-4-4 Písaři (11 bodů)

Před vynálezem knihtisku se knihy nemohly tisknout, ale musely se ručně opisovat. To byla dosti zdlouhavá práce. Například pokud herci chtěli sehrát nějakou divadelní hru, musel režisér nejdříve zajistit opis scénáře pro každého herce. Protože ale písaři stojí peníze, bylo zvykem dát každému herci pouze tu část scénáře, kterou skutečně potřebuje. Rozdělit opisování kusů scénáře mezi jednotlivé najaté písaře se tím ovšem zkomplikovalo. Proto jste byli přes propast času požádáni, abyste režisérovi pomohli.

Vaším úkolem je napsat program, který dostane na vstupu počet herců N, počet písařů K a dále pro každého herce počet stránek, které je pro něj třeba opsat. Vaším úkolem je každému písaři přiřadit herce, pro které má opsat jejich části scénáře tak, aby celkově opisování trvalo co nejméně (tedy aby maximum přes počty stránek pro jednoho písaře bylo co nejmenší). Navíc písaři píší různě pěkně a váženější herci by měli dostat hezčeji napsané scénáře. Proto musí první písař opisovat scénář pro herce 1,… ,h1, druhý písař pro herce h1+1,… ,h2 atd.

Příklad: Pro 7 herců, 3 písaře a počty stránek 8, 4, 3, 5, 6, 2, 9 je nejrychlejší, aby první písař opisoval scénař pro první dva herce, druhý písař pro další tři herce a poslední písař pro poslední dva herce.

Řešení

15-4-5 Haskell (10 bodů)

Prozatím jsme se zabývali tím, jak se Haskell (a mnohé další alespoň přibližně čisté funkcionalní programovací jazyky) chovají navenek. Nyní se podíváme, co se děje uvnitř – tj. jak se tyto jazyky kompilují.

Už na úvod si řekněme, že těžko. Nejlepší současné překladače produkují kód, který bývá 5× – 10× pomalejší než odpovídající program v C, a také s výrazně vyššími paměťovými nároky. Toto je samozřejmě nefér srovnání – C je jazyk navržený pro zcela jiné účely než Haskell (a bohužel také pro jiné účely, než na které je v praxi používán). Nicméně ani srovnání s jinými imperativními jazyky nevypadá příznivě. Z větší části je to ovšem způsobeno tím, že současné počítače jsou navrženy tak, aby vyhovovaly imperativním, kódem řízeným výpočtům. Pro deklarativní jazyky by byly mnohem užitečnější daty řízené počítače, které se ovšem příliš nevyskytují (a v dohledné době zřejmě nebudou). Zaměřme se tedy na problémy, které se nám při kompilaci objevují, a způsoby jejich řešení.

V líně vyhodnocovaném jazyce nelze dopředu rozhodnout, které výpočty se pro daný vstup vlastně provedou. Víceméně nemáme jinou možnost, než provádět vždy jen ty výpočty, které právě potřebujeme – z toho ovšem plyne nutnost „odkládat“ si rozpracované výpočty stranou. Podívejme se na konkrétní příklad:

{- 1 -} jedničky = 1 : jedničky
{- 2 -} take 0 x = []
{- 3 -} take n x =
           case x of
             (h:t) -> h : take (n-1) t

Vyhodnocujme take 3 jedničky. Nejprve se provede 3. řádek; je tedy potřeba vyhodnotit case jedničky of (h:t) -> h : take (n-1) t. Toto vyžaduje zjistit, zda seznam jedničky není prázdný. Kvůli tomu provedeme jeden krok řádku 1. Nyní opět vyhodnocujeme řádek 3 – take 2 t, kvůli tomu musíme provést další krok na řádku 1, atd. – ve vyhodnocování se střídají jedničky a take. Všimněme si několika faktů:

Další věcí, kterou je třeba mít na paměti, je sdílení. Když napíšeme

let x = výpočet in x + x

chceme, aby se výpočet provedl jen jednou. To můžeme (ve spojení s líným vyhodnocováním) realizovat tak, že na místo, kde bude uložena hodnota x, si nejprve uložíme odložený výpočet, který navíc rozšíříme tak, že po svém dokončení tuto pozici přepíše hodnotou výsledku. Kvůli tomu ovšem musíme při každém přístupu k proměnné testovat, zda už byla vyhodnocena, což nám samozřejmě na rychlosti nepřidá. Asi nejelegantnější způsob, jak to jde v praxi realizovat, je ten, že vždy bude na místě proměnné uložen nějaký výpočet. Nejprve to bude ten, který vyhodnotí výpočet, a následně se přepíše triviálním výpočtem, který pouze vrací spočítaný výsledek. Tím se vyhneme testování, zda již byl výpočet proveden (na úkor toho, že vždy musíme provést zavolání funkce).

Další zdroj potíží je v předávání funkcí. Samotné funkce příliš velký problém nepředstavují (když už stejně musíme umět odkládat výpočty), nicméně musíme nějak zajistit předávání parametrů. Ty si musíme ukládat u příslušného „odloženého“ výpočtu. Parametry se nám mohou hromadit postupně, a navíc se nám jich může nakupit víc, než kolik potřebuje daná funkce – v případě, když vrací jinou funkci. Například

plus x y = x + y
id x = x
vysledek = map (id plus 5) [1, 2, 3]   - - = map (plus 5) [1, 2, 3] = [6, 7, 8]
se bude vyhodnocovat tak, že nejprve vytvoříme odložený výpočet (anglicky „thunk“, nejsem si jistý českým ekvivalentem) pro funkci id s parametry plus a 5. Později při vyhodnocování seznamu se z něj vyrobí nový thunk s parametry plus, 5, 1; pak se vyhodnotí id, spolkne první parametr a vrátí thunk pro funkci plus se zbývajícími parametry. Povšimněte si, že thunk nejde jen přepsat na místě, protože ho ještě budeme potřebovat při vyhodnocování dalšího prvku v seznamu. To se dá řešit buď zkopírováním starého thunku, nebo tím, že si parametry ukládáme ve spojovém seznamu. To může být rychlejší a úspornější – není potřeba kopírovat parametry, nicméně práce se spojovým seznamem je pomalejší, takže tyto výhody se projeví jen u funkcí s mnoha parametry. Navíc je složitější provést vyhodnocení thunku a také správa paměti (garbage collecting) se komplikuje.

Jak jste již zajisté uhodli, úkolem v této sérii bude napsat jednoduchý kompilátor. Nebudeme samozřejmě překládat celý Haskell, jen jeho malou podmnožinu (nicméně dostatečně velkou, aby do ní šla relativně snadno podstatná část Haskellu přeložit), ani se nebudeme zabývat takovými detaily (ve skutečnosti hodně zajímavými a důležitými) jako parsing, kontrola a odvozování typů a podobně. Také stroj, pro nějž budeme programy překládat, bude zvládat operace o něco vyšší úrovně, než je běžné – některé z nich jsou přímo navrženy tak, aby zjednodušily řešení výše uvedených problémů.

Program dostaneme zadaný jako seznam prvků typu Equation

data Equation = Equation String [String] Expression
             - - Equation jméno_funkce parametry definice

Každá funkce je definována nanejvýš jednou. Parametry jsou prostě jména (tj. nedělá se tu pattern matching). Definice (typu Expression) je výraz, kterým je funkce definována. Hodnoty všech výrazů jsou celá čísla nebo funkce. Typ Expression je definován takto:

data Expression = Let [Equation] Expression |   - - Let definice výraz
                                                - - dělá totéž jako let definice in výraz
                  Apply Expression Expression | - - Apply funkce parametr
                                                - - aplikace funkce na daný parametr
                  Number Int |                  - - číslo
                  Variable String |             - - odkaz na proměnnou
                  Plus Expression Expression |  - - sečte dva výrazy
                  Mul Expression Expression |   - - násobí dva výrazy
                  Minus Expression Expression | - - odečte dva výrazy
                  Div Expression Expression |   - - dělí dva výrazy
                  Case Expression [(Int, Expression)] Expression
                                                - - Case výraz alternativy default
                                                - - podrobnější popis viz níže

Sémantika většiny příkazů je jasná – Let zavádí lokální definice, Apply je aplikace funkce, Number je celočíselná konstanta, Variable je hodnota, která je aktuálně uložena v dané proměnné, Plus/Minus/Mul/Div jsou aritmetické funkce. Case je výběr z více alternativ na základě hodnoty výrazu – zvolí se ta z alternativ, jejíž hodnota odpovídá, a vrátí se vybraný výraz; pokud neodpovídá žádná, vrátí se hodnota default.

Poznámka stranou – všimněte si, že se nezabýváme složitějšími typy. To je jednak pro zjednodušení, jednak proto, že se bez nich dá obejít. Například seznamy lze naprogramovat tímto způsobem:

cons hlava tělo = let h = hlava
                      t = tělo
                   in \sel -> if sel then h else t
head list = list True
tail list = list False

Tohle samozřejmě není korektní program v Haskellu – nejde otypovat. Nicméně v našem jazyce už typy nejsou, takže to nevadí. Let v definici funkce cons je nutný, abychom zajistili sdílení jednou spočítaných hodnot.

Příklad kompilovaného programu:

[
  Equation "mod" ["x", "y"]
     (Let [
            Equation "p" [] (Div (Variable "x") (Variable "y")),
            Equation "s" [] (Mul (Variable "p") (Variable "y"))
          ]
        (Minus (Variable "x") (Variable "s"))),
    - - mod x y = let p = x `div` y
    - -               s = p * y
    - -            in x -
s Equation "nsd" ["x", "y"]
     (Case (Variable "x")
        [(0, Variable "y")]
        (Let [
               Equation "p" [] (Apply
                                 (Apply (Variable "mod") (Variable "y"))
                                 (Variable "x"))
             ]
           (Apply (Apply (Variable "nsd") (Variable "p")) (Variable "x"))))
    - - nsd x y = case x of
    - -             0 -> y
    - -             _ -> let p = mod y x
    - -                   in nsd p x
]

Výsledkem kompilace by měl být program pro stroj, který vypadá takto: Má několik oddílů paměti; všechny se skládají z více položek, které jsou očíslovány přirozenými čísly.

Kromě toho obsahuje seznam, v němž se nachází aktuálně vykonávaný kód. Stroj funguje tak, že vždy z tohoto seznamu odebere první instrukci, provede ji a celý postup opakuje. Stroj se zastaví, jestliže tento seznam bude prázdný. Dále má stroj ještě zásobník, do nějž si ukládá registry při volání funkce; ten je na počátku vždy prázdný.

Počáteční stav stroje je uložen v proměnné typu InitialState:

data InitialState =
        InitialState [(Int,Int,[Instruction])]   - - paměť pro kód
                     [(Int,Value)]               - - paměť pro data
                     [(Int,Int)]                 - - registry
                     [Instruction]               - - aktuální kód
data Value = VNumber Int |
             VThunk Int [Int]

„Program“ pro tento stroj je vlastně definice jeho počátečního stavu.

Instrukce jsou tyto (pod [x] rozumíme hodnotu uloženou v paměti na adrese, obsažené v registru x).

data Instruction =
       IMove Int Int |
         - - IMove from to
         - - přesuň hodnotu z registru from do registru to
       IPlus Int Int Int |
         - - IPlus x y ret
         - - naalokuj novou položku v datové paměti, vlož do ní součet [x] a [y]
         - -  ([x] a [y] musí být čísla, tj. ne thunky) a adresu této položky
         - -  vlož do registru ret
       IMinus Int Int Int |
       IMul Int Int Int |
       IDiv Int Int Int |
         - - analogicky pro ostatní operace
       IExecute Int |
         - - IExecute w
         - - pokud [w] je číslo: vlož w do registru 0
         - - pokud [w] je thunk, obsahující adresu k do kódové paměti a seznam
         - -  parametrů l: buď n počet parametrů položky k z kódové paměti,
         - -  c kód tam uložený. Je-li n menší než délka l, vlož w do registru 0
         - -  jinak
         - -    odlož obsah registrů na zásobník
         - -    smaž registry
         - -    do registrů 1 až n vlož prvních n prvků l
         - -    zbytek l ulož na zásobník
         - -    c připoj na začátek aktuálního kódu
       IReturn |
         - - smaž všechny registry až na 0
         - - ostatní registry obnov ze zásobníku
         - - jestliže je seznam parametrů uložený na zásobníku neprázdný, přidej
         - -  je na konec seznamu parametrů thunku [0] ([0] musí být thunk)
         - - na začátek aktuálního kódu připojí instrukci IExecute 0
       ICExecute Int Int Int |
         - - ICExecute x y w
         - - pokud [x] == [y] ([x], [y] musí být čísla), vlož instrukci IExecute w
       ICall Int Int |
         - - ICall k reg
         - - naalokuj novou položku v paměti, vytvoř na ní thunk obsahující
         - -  odkaz k do paměti pro kód a prázdný seznam parametrů. Adresu
         - -  této položky vlož do registru reg
       ILoad Int Int |
         - - ILoad val reg
         - - naalokuj novou položku v paměti, vytvoř na ní číslo val a adresu
         - -  této položky vlož do registru reg
       IApply Int Int Int |
         - - IApply t p reg
         - - vezmi thunk [t], zkopíruj ho na nově vytvořené místo v datové paměti,
         - -  na konec seznamu parametrů kopie přidej adresu z registru p a
         - -  adresu této kopie vlož do registru reg
       IRewrite Int Int
         - - IRewrite what with
         - - položku v datové paměti s adresou uloženou v registru what přepiš
         - -  hodnotou [with]

Vaším úkolem je napsat funkci

compile::[Equation]->Expression->InitialState

která dostane na vstup program a výraz ve výše uvedeném tvaru a výsledkem bude počáteční stav stroje takového, že hodnota výrazu bude na konci jeho výpočtu v [0].

Řešení