Pátá série dvacátého druhého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 22-5-1: Turnaj
- 22-5-2: Stráže údolí
- 22-5-3: Zrcadla
- 22-5-4: Davy lidí
- 22-5-5: Čokolámání
- 22-5-6: Hlídači princezny
- 22-5-7: ArcheoPaleoLingua
22-5-1 Turnaj (Zadání)
Vaše řešení (která byla tentokrát takřka výhradně správná) vykazovala velké odchylky v délce: zatímco si někteří vystačili s pěti větami, jiní popsali stránku. Vzhledem k obtížnosti úlohy si vážíme obou přístupů, ale odbytí těžšího příkladu krátkým textem vidíme velmi neradi.
Zadání klade návodné otázky, které nyní zodpovíme:
Jací jsou kandidáti na druhé místo? Evidentně právě ti draci, kteří prohráli s vítězem. Všichni ostatní totiž byli (třebas nepřímo) poraženi některým z těchto poražených draků a nejlepší tabulkové místo, na které mohou dosáhnout, je třetí. Z této množiny pak zároveň nemůžeme bez dalšího zkoumání žádného draka vyřadit, protože spolu zápas jistě nehráli, ani se libovolný z nich nemůže nacházet v podstromu libovolného jiného, takže si je nemůžeme nijak uspořádat.
Kolik takových kandidátů je? Jej, to je záludné. Zadání se explicitně nezmiňuje o tom, že by byl pavouk hry úplný binární strom, obrázek však k takovému pojetí vede. Při opravování jsem tedy akceptoval jak názor, že je těchto kandidátů logaritmicky vůči počtu zúčastněných draků, tak názor, že se to nedá moc dobře říct, jelikož strom může vypadat všelijak.
Jak mezi nimi co nejefektivněji vybrat druhého draka? To naopak záludné není vůbec: prostě sestavíme herní strom pro draky poražené výhercem. Vzhledem k jejich počtu N bude potřeba sehrát N-1 utkání (každé vyřadí právě jednoho draka), vzhledem k počátečnímu počtu draků tedy v případě úplného stromu máme logaritmický počet nutných dohrávek.
22-5-2 Stráže údolí (Zadání)
V tejto úlohe sme mali zadané body na priamke, vedeli sme medzeru medzi každými dvoma susednými a chceli sme odstrániť maximálne K z nich, aby sme maximalizovali najkratšiu medzeru medzi tými bodmi, ktoré zostanú.
Táto úloha rovnako ako mnoho iných úloh má jednoduché, rýchle, ale pritom nesprávne greedy riešenie, ktoré je založené na postupnom odstraňovaní bodov susediacich s najkratšou medzerou (skúste si nájsť protipríklad).
Jednoduché korektné riešenie vieme naprogramovať pomocou dynamického programovania, kde stav výpočtu je dvojica (n,k) a pre každú dvojicu chceme spočítať optimálne riešenie, ak sme spracovali prvých n bodov a vyhodili sme práve k z nich. Takáto úvaha vedie na riešenie so zložitosťou O(N2 K), ale stále má ďaleko od vzorového riešenia.
Naše vzorové riešenie využíva myšlienku, ktorá sa používa vo veľa problémoch, kde spočítať samotné riešenie problému je pomerne zložité, zato však overiť, či existuje riešenie s požadovanou vlastnosťou, je pomerne jednoduché.
V našom príklade vieme ľahko overiť, či existuje riešenie, ktoré odstráni maximálne K bodov z daných a má minimálnu vzdialenosť aspoň takú ako pevne dané M. Zodpovedanie tejto otázky vieme previesť na iný známy problém „plánovania intervalov“: Máme zadaných N intervalov v čase, pričom každý začína v čase ai a má dĺžku bi. Pričom z týchto intervalov chceme vybrať maximálny počet tak, že žiadne dva vybraté intervaly sa neprekrývajú.
Prevod je nasledovný: všetky čísla ai sú rovné pozíciam bodov na priamke a všetky bi sú rovné M. Ak nájdeme riešenie tohto problému, potom sme našli maximálnu množinu bodov (počiatky intervalov), ktoré sú od seba vzdialené aspoň M. Pričom keď sme našli takéto riešenie, ktoré maximalizovalo počet vybratých intervalov (bodov), potom súčasne toto riešenie minimalizuje počet intervalov (bodov), ktoré sme nevybrali. Teda po nájdení riešenia, vieme zodpovedať otázku, či existuje riešenie, ktoré má najmenšiu vzdialenosť aspoň M, podľa toho, či naše riešenie „plánovania intervalov“ nevybralo maximálne K intervalov.
Treba však vedieť riešiť samotný problém plánovania intervalov. Na tento problém je však známy jednoduchý greedy algoritmus: Na začiatku si utriedime body podľa času konca intervalu, následne začneme tieto intervaly prechádzať v tomto poradí a súčasne si budujeme riešenie (množinu vybratých intervalov) použitím jednoduchého pravidla: pri prechádzaní, vždy keď môžeme práve spracovávaný interval pridať k budovanému riešeniu, tak ho tam pridáme. Toto sa dá po usporiadaní intervalov vykonať v lineárnom čase od počtu intervalov, stačí si vždy len pamätať čas konca posledného intervalu v našom budovanom riešení. Naviac v našom špeciálnom prípade majú všetky intervaly rovnakú dĺžku, takže stačí usporiadať intervaly podľa začiatku (na vstupe však už máme pozície utriedené a v našej úlohe nemusíme triedenie vôbec riešiť).
Teraz už vieme zodpovedať otázku, či existuje riešenie s danou minimálnou vzdialenosťou. K čomu nám to poslúži? Treba si všimnúť, že ak existuje riešenie, ktoré má minimálnu vzdialenosť aspoň M, potom existuje riešenie, ktoré má minimálnu vzdialenosť M' pre každé M' ≤ M (jednoducho ponecháme rovnakú množinu bodov). Inak povedané, existuje číslo M* také, že pre všetky M ≤ M* riešenie existuje a pre všetky M > M* riešenie neexistuje. A práve čislo M* hľadáme. Teda riešenie by sme mohli nájsť tak, že ak máme rozsah súradníc bodov z nejakého intervalu R, potom vieme postupným skúšaním existencie riešenia, ktoré má minimálnu vzdialenosť R, R-1, R-2, …, nájsť číslo R* v čase O(RM). Avšak z vlastnosti hľadaného čísla M* môžeme použiť binárne vyhľadávanie na intervale R. Keď si pre medián prehľadávaného intervalu riešení zistíme, či existuje riešenie, pak sa na základe toho vieme rozhodnúť, v ktorej polovici prehľadávaného intervalu leží číslo M*.
Takto vieme nájsť maximálnu minimálnu vzdialenosť medzi dvojicou bodov a body, ktoré máme odstrániť, sú počiatky nevybratých intervalov pri riešení príslušného podproblému plánovania intervalov.
Celková časová zložitosť je O(N log R), kde pri binárnom vyhľadávaní na intervale dĺžky R vieme v lineárnom čase overiť existenciu riešenia. Pamäťová zložitosť je O(N).
22-5-3 Zrcadla (Zadání)
Máme čtvercovou síť a hledáme v jistém smyslu nejkratší cestu, respektive cestu s co nejméně „zatáčkami“ tvořenými zrcadly. Že by prohledávání do šířky? Tak se podívejme, jak ho realizovat v tomto případě. Pokud jste ještě žádné prohledávání do šířky nikdy nepotkali, podívejte se do grafové kuchařky na našich stránkách.
Jak se dá čekat, ve frontě, již používá prohledávání do šířky, budou jednotlivá políčka čtvercové sítě a každé se tam dostane maximálně jednou, fronta tedy může narůst do velikosti až O(M ×N). Vždy, když odebereme políčko z fronty, pustíme z něj světlo do všech čtyř směrů (do některých políček může přijít světlo z různých směrů přes stejný počet zrcadel a ukládat ho do fronty dvakrát se nevyplácí). Pro každý směr postupně procházíme políčka, dokud nenarazíme na překážející dům, a zařazujeme je do fronty, jestliže v ní ještě nebyly. Když narazíme na dům, jejž chceme osvítit, vypíšeme počet zrcadel a skončíme. Vyprázdní-li se fronta a cíl je nedosažen, nejde na něj dosvítit.
Pro evidenci, kde se nacházejí překážky a přes kolik zrcadel došel algoritmus na konkrétní políčko, si zavedeme dvourozměrné pole o velikosti M ×N. Hodnota -3 na políčku i,j znamená, že je tam překážka, hodnota -2, že do políčka ještě nedorazilo světlo, a hodnoty větší nebo rovné nule, přes kolik nejméně zrcadel se tam světlo dostane.
Proč toto řešení funguje? Stačí, když si všimneme, že políčka ve frontě jsou uspořádána dle minimálního počtu zrcadel, která musíme použít, aby se do nich dostalo světlo. Pokud jsme se na políčko A dostali nejprve z políčka B a dostaneme-li se do něj později z jiného bodu, určitě k tomu použijeme nejméně tolik zrcadel jako z políčka B.
Jaká je časová složitost tohoto algoritmu? Každé políčko se sice objeví ve frontě maximálně jednou, ale světlo se z něj může dostat až do O(M + N) dalších políček. Navíc na každé políčko může doletět světlo až z O(M + N) jiných, celkově tedy vyjde ne moc pěkná složitost O(MN(M + N)).
Jak algoritmus zrychlit? Hlavní problém, proč algoritmus pracuje v nejhorším případě tak pomalu, je, že se na některá políčka podíváme až O(M+N)-krát, avšak do fronty je zařadíme jen jednou. Přitom je zbytečné se na ně dívat ze stejného směru vícekrát (např. z políčka, jež je nad ním, pak z toho, co je o 2 nad ním…). Proto si budeme u každého políčka navíc ukládat, jakými všemi směry už jím letělo světlo.
Můžete si všimnout, že stačí ukládat pouze dva bity informace: jestli políčkem letělo světlo horizontálním směrem a jestli vertikálním směrem. Pokud totiž poletí světlo z políčka v souvislém úsek bez překážek na nějakém řádku či sloupci, tak ho proletí celý bez ohledu na to, odkud se naposledy mohlo odrazit.
S tímto vylepšením se po vytažení políčka z fronty podíváme, jestli už jím proletělo světlo horizontálním i vertikálním směrem a případně projdeme políčka tím či oním směrem (oběma zároveň určitě ne kromě zdroje, jelikož světlo muselo do políčka nějakým směrem doputovat). Díky vlastnostem prohledávání do šířky (políčka jsou ve frontě seřazena dle počtu zrcadel, přes která se do nich dostalo světlo) jsme si touto úpravou určitě nepokazili řešení.
Nyní už do každého políčka doputuje světlo nejvýše dvakrát, takže časová složitost vyjde O(MN). V nejhorším případě stejně projdeme skoro celou čtvercovou síť a ostatně i velikost vstupu je nejvýše O(MN) (bude-li řádově tolik překážek), takže asymptoticky lepší algoritmus vymyslíme jen těžko, pomineme-li nějaké heuristiky (triky, které v určitých případech zrychlí program), jež však obecně nefungují.
22-5-4 Davy lidí (Zadání)
Úloha byla věru těžká. Vyřešíme tedy nejdříve několik podproblémů a z nich pak složíme celé řešení. Výklad okořeníme tímto značením: jsou-li A a S body v rovině, pak AS značí obraz bodu A ve středové souměrnosti se středem S.
1. Je množina bodů symetrická podle zadaného středu S? To můžeme zjistit snadno: uložíme body množiny do nějaké datové struktury (třeba do vyhledávacího stromu). Pak je budeme postupně procházet body a pro každý bod A se podíváme, je-li ve struktuře i bod AS. Pokud ano, oba smažeme a pokračujeme dál. To pro n bodů zvládneme v čase O(n log n).
Můžeme to provést i jednodušeji: Setřídíme body lexikograficky (tzn. nejdříve podle x-ové souřadnice a kde je x stejné, tam podle y) a všimneme si, že pokud je bod A lexikograficky před B, pak je BS lexikograficky před AS. Jinými slovy v setříděném pořadí platí, že obraz prvního bodu je poslední bod, obraz druhého předposlední a tak dále. Tříděním strávíme čas O(n log n), kontrolou pak O(n). To je výhodnější v případě, že chceme postupně vyzkoušet několik různých kandidátů na střed S.
2. Je množina bodů symetrická? To bude snadné – pokud je množina symetrická, musí její těžiště ležet ve středu symetrie. Stačí tedy spočítat těžiště (jeho x-ová souřadnice je průměrem x-ových souřadnic všech bodů a podobně y-ová souřadnice) a spustit na něj předchozí algoritmus.
3. Známe polohu sochy S a fontány F, lze body rozdělit na část souměrnou podle S a část souměrnou podle F? Zde naprostá většina řešitelů zkusila hladový algoritmus – testovat už známým způsobem souměrnost podle S, body, které souměrné nejsou, si dávat stranou a nakonec vyzkoušet, jestli jsou souměrné podle F. To ale bohužel nefunguje, elá hop, protipříklad z klobouku ven:
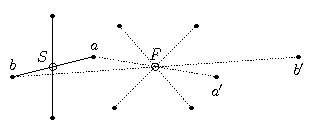
Body a, b se účastní dvou symetrií – jednak spolu podle S, jednak s a', b' podle F. Pokud tedy při zkoumání středu S body a, b spárujeme, zbudou pak a' a b' na ocet. Kdybychom je ovšem odložili oba stranou, spárovali bychom následně podle středu F dvojice a–a' a b–b'. (Zde by samozřejmě pomohlo zkoumat nejdřív F a pak S; takový algoritmus ale nachytáme, pakliže k našemu protipříkladu přidáme ještě jeho kopii překlopenou podle osy úsečky SF.)
Jak z téhle arcipatálie ven? Inu, za vším hledej grafy… body prohlásíme za vrcholy, dvojice symetrické podle S spojíme jedním typem hran (na obrázku plné čáry), dvojice symetrické podle F druhým (na obrázku tečkovaně). V tomto grafu chceme najít perfektní párování, čili rozdělit vrcholy na dvojice tak, aby každá dvojice byla spojena hranou.
Žádný problém, každý matfyzák ví už od narození, že na hledání perfektního párování tu je Edmondsův „zahradní“ algoritmus. My ale tak mocné kouzlo ani nebudeme potřebovat. Místo toho si zkusíme představit, jak náš graf vypadá. Kterýkoliv vrchol může sousedit s nejvýše jednou hranou prvního druhu a nejvýše jednou druhého. Stupeň vrcholu tedy může být buď 0, nebo 1, nebo 2 a pokud je 2, jsou obě hrany různých druhů. To nám nedává moc možností – každá komponenta souvislosti musí být buďto izolovaný vrchol nebo cesta, případně kružnice. Na cestě i na kružnici se navíc musejí střídat hrany obou druhů, takže ihned víme, že kružnice mají sudou délku a tím pádem si na nich stačí vybrat buď jeden nebo druhý druh hran a je spárováno. Cesty o sudém počtu hran a izolované vrcholy (to jsou vlastně cesty o nula hranách) spárovat určitě nejdou. Na cestě o lichém počtu hran stačí použít ten typ hrany, kterým cesta začíná i končí.
K vyřešení tohoto podproblému tedy postačí sestrojit pomocný graf (třeba dvojím spuštěním algoritmu 1.), rozložit ho na komponenty souvislosti a ověřit, jestli se mezi nimi nevyskytne sudá cesta. To vše zvládneme v čase O(n), pokud už máme všechny body setříděné lexikograficky.
4. Polohy S, F neznáme. Co teď? Budeme pokorně zkoušet všechny kandidáty na polohu sochy a fontány a spouštět pro ně předchozí ověřovací algoritmus. Není jich nekonečně mnoho? Ne ne, střed přeci musí ležet buďto v nějakém zadaném bodě nebo ve středu úsečky určené dvěma zadanými body. Takových míst je O(n2), takže dvojic kandidátů na S, F je O(n4), ověřováním každé strávíme O(n). Celková časová složitost je tedy O(n log n + n5) = O(n5), paměti nám stačí lineárně.
5. Zrychlujeme. Jak se zbavit obludné páté mocniny, jež nám škodolibým chechtotem kazí radost z vítězství? Trochu množinu kandidátů na středy omezíme. Předně – zvolíme si nějaký pevný bod A a prohlásíme, že socha je to, podle čeho je tento bod souměrný. Stačí tedy při hledání poloh sochy vyzkoušet jen středy úseček, kterých se bod A účastní. Pro každou polohu sochy pak nalezneme nějaký bod, který podle ní není s ničím symetrický (kdyby žádný takový nebyl, už jsme úlohu vyřešili). Tento bod jistě patří do druhé množiny, takže fontána se vyskytuje na nějaké úsečce vedoucí z tohoto bodu. Celkem tedy O(n) možností pro sochu, O(n) pro fontánu a čas O(n) na ověření. To dává dohromady O(n log n + n3) = O(n3) s lineární pamětí. Umíte to lépe? My zatím ne.
22-5-5 Čokolámání (Zadání)
Předtím, než určíme, kolik vlastně rozlámání celé čokolády nejméně stojí, musíme vymyslet, jak takové rozlámání provést. Velice jednoduché řešení je jít na čokoládu „hladově“. Vzhledem k tomu, že zlomy, které provedeme dříve, se započítají méněkrát než ty, co provedeme později, tak čokoládu rozlomíme vždy podle nejdražšího zatím nepoužitého zlomu. Pokud zlom prochází přes víc kusů čokolády, rozlomíme každý z nich. Jenže takovýhle jednoduchý postup přece nemůže fungovat, ne? Ukazuje se, že může, jenom to musíme dokázat.
Nějaký konkrétní postup rozlámání si můžeme představit dvěma způsoby: buď jako binární strom, kde každý vrchol je kus čokolády, synové vrcholu jsou ty kusy, které z něj vzniknou jedním rozlomením, a listy jsou kusy, které už nejdou rozlomit (tzn. velikosti 1 ×1). Druhou reprezentací postupu rozlámání je posloupnost zlomů, ve které se každý zlom vyskytuje právě jednou.
Převedení posloupnosti zlomů na strom je jednoduché: lámeme čokoládu podle
zlomů v posloupnosti a všímáme si, které kusy jsme rozlomili na jaké. Opačný
směr je ovšem složitější: posloupnost zlomů určíme ze stromu tak, že
rekurzivně vypočítáme posloupnosti zlomů podstromů synů kořene, ty spojíme a
na začátek ještě přidáme zlom z kořene. Spojení je definované tak, že obě
posloupnosti musí být podposloupnostmi (ne nutně souvislými) výsledku s tím,
že se v něm žádný zlom nesmí opakovat, ale na druhou stranu můžeme změnit
pořadí v rámci souvislých skupin zadaných posloupností, které obsahují pouze
zlomy jedné orientace. Když vodorovné zlomy budu značit písmeny a svislé
čísly, tak například posloupnosti DCA1B a C3ABD přeuspořadám na CAD1B a
C3ADB a výsledkem je C3AD1B, posloupnosti A1B a B3A spojit nejdou a
strom, který obsahuje takové podstromy, nejde reprezentovat jako posloupnost
zlomů. Když postup rozlámání reprezentovaný stromem převedu na posloupnost
zlomů a pak zpět na strom, výsledkem může být jiný strom. Jejich ceny ale
budou stejné, protože jsme jenom změnili pořadí v rámci skupin zlomů se
stejnou orientací. (Když lámu zleva doprava, tak výsledek má stejnou cenu,
jako když lámu zprava doleva. Když ale nejdřív lámu vodorovně a pak svisle,
tak výsledek může mít různou cenu, než když lámu v opačném pořadí.)
Náš postup rozlámání se reprezentuje jako posloupnost zlomů jednoduše: jsou to všechny zlomy setříděné od nejdražšího. Nyní potřebujeme dokázat, že tato posloupnost zlomů je nejlevnější možná a také, že žádný postup rozlámání, který se nedá vyjádřit jako posloupnost zlomů, nejlevnější být nemůže.
Všimneme si, že jakoukoliv posloupnost můžeme setřídit tak, že vezmeme prvek s nevyšší hodnotou a přesuneme jej na první místo, pak vezmeme prvek s druhou nejvyšší hodnotou a dáme ho na druhé místo a tak dále. Při každém takovém přesunutí prvek přeskakuje jen prvky, které mají menší hodnotu, než on sám. Pokud jsou prvky posloupnosti zlomy, tak platí, že přeskočení zlomu, který má stejnou orientaci cenu nezmění. Na druhou stranu přeskočení zlomu s opačnou orientací způsobí, že počet výskytů přeskakujícího zlomu ve stromové reprezentaci se zmenší o jedna, naopak počet výskytů přeskakovaného zlomu se o jedna zvýší. A protože počet výskytů ve stromě odpovídá tomu, kolikrát se zlom započítá do výsledné ceny, určitě jsme takovýmto setříděním posloupnosti zlomů její cenu nezvýšili. Jako výsledek jsme dostali naši posloupnost, ta je tedy určitě nejlevnější.
To, že postup rozlámání, který nejde reprezentovat posloupností zlomů, nemůže být nejlevnější, dokážeme tak, že si ve stromě, který reprezentuje takovýto postup, najdeme vrchol, jehož podstrom reprezentovat posloupností nejde, ale podstromy obou jeho synů jdou (takový určitě existuje). Alespoň jedna z posloupností synů není setříděná od nejdražšího (kdyby obě byly, tak jdou spojit) a navíc se ani nedá setřídit přehazováním v rámci souvislých skupin se stejnou orientací. To znamená, že tam buď existuje dvojice po sobě jdoucích zlomů s opačnou orientací, jejíž první prvek má menší cenu, nebo se taková dvojice dá vytvořit přehazováním ve skupině se stejnou orientací. Když tuto dvojici prohodím, zmenším tím cenu rozlámání, a tento postup tedy nemohl být nejlevnějším.
Dokázali jsme tedy, že náš postup je nejlevnější, teď už zbývá jenom vymyslet, jak spočítat tuto cenu. Stačí si uvědomit, že každý zlom v posloupnosti se započítá o jedna víckrát, než kolik je před ním zlomů s opačnou orientací. Algoritmus bude postupovat tak, že si všechny zlomy setřídí podle ceny a postupně je od nejdražšího započítává, každý tolikrát, kolik zlomů podle opačné osy, než má aktuální zlom, jsme už započítali. Pokud má čokoláda rozměry M ×N, tak časová složitost je O((N+M) log(N+M)) a paměťová O(N+M).
Poznámka: Setřídění zlomů podle ceny jsme docela odbyli, jaký třídící
algoritmus je nejlepší? Vzhledem k tomu, že tato úloha je praktická, tak
odpověď je velice jednoduchá: obvykle ten, který programovací jazyk, který
používáme, sám obsahuje. Třeba v Céčku je to qsort(), v C# Array.Sort().
22-5-6 Hlídači princezny (Zadání)
Začneme, jako každý líný člověk, od toho nejjednoduššího. Představme si, že máme hlídače, řekněme A, kterého nekryje vůbec nikdo. Ten určitě do útoku jít nemůže. Tak tam ale do útoku pošleme hlídače B, který je kryt hlídačem A (pokud již v útoku není). Oba ze vstupu odstraníme, protože jsou již vyřešení a pokračujeme s menší úlohou stejného druhu.
Co ale v případě, že žádného nekrytého nemáme? Pak si všimneme, že takový graf musí být několik nepropojených orientovaných cyklů. Vezmeme tedy každý z cyklů zvlášť (můžeme, neovlivňují se). Když je cyklus sudé délky, pak dokážeme poslat do útoku právě polovinu z jeho hlídačů (každého druhého) – lépe to zřejmě nejde, za každého v útoku musí být alespoň jeden, který kryje. A u lichého? Tam nám, bohužel, jeden zbude, ale ať párujeme jakkoliv, jeden zbýt musí, tedy to také nejde lépe.
Že mi ještě nevěříte? No, tak malinko důkazů. Napřed si dokážeme, že pokud v grafu není žádný vrchol vstupního stupně 0 a všechny mají výstupní stupeň 1, pak se jedná o cykly. Vyberme si libovolný vrchol. Z něho vede právě jedna hrana ven. Vydejme se po ní a dojdeme do dalšího. A tak dále. Jednou musíme potkat vrchol, ve kterém jsme již byli. A proč je to ten první? Kdyby nebyl, tak do toho, který jsme potkali podruhé, vedou alespoň dvě různé hrany (jedna, po které jsme přišli poprvé a druhá, kterou jsme přišli teď). Protože ale z každého vrcholu vychází právě jedna hrana, průměrně do každého musí také vstupovat jedna. A neexistuje vrchol, který by měl méně než jednu vstupní hranu, nemůže tedy existovat ani takový, který má více než jednu.
A nyní to tvrzení hned na začátku. Proč můžeme vzít hlídače B? Hledáme nejmenší protipříklad – vstup s nejmenším počtem hlídačů, kde náš program vybere špatné řešení. Hlídače B jsme vybrali a zkazili jsme to tím – to ale znamená, že byl potřeba v záloze na krytí hlídače C.
No dobrá, ale tím, že místo C vezmeme B, si přeci neuškodíme. Hlídačů máme stejně a po nasazení B nám v grafu zbude jeden vrchol navíc (což nám, zřejmě, neuškodí, protože ho můžeme jednoduše nevyužít).
To je celé hrozně hezké, víme, že to funguje. Jak to ale napsat? A to ještě tak, aby to běželo rychle? Samozřejmě, mohli bychom pokaždé projít celý vstup, pokusit se najít vrchol stupně 0, ale to by trvalo dlouho. Proto je na to potřeba jít chytřeji.
Předpočítáme si, hned na začátku, vstupní stupeň každého vrcholu. Poté si rozházíme vrcholy na dvě hromádky – v jedné budou ti nekrytí a v druhé ti ostatní.
Potom zkusíme vzít vždy jednoho nekrytého. Toho dáme do zálohy (to je náš A). Pokud je ten, kterého kryje, ještě nezpracovaný, nasadíme ho do útoku (to je B). A tomu, kterého kryje B, odečteme jedničku od vstupního stupně, pokud mu klesne na nulu, přehodíme z jedné hromádky do druhé. Celý tento jeden krok lze stihnout v konstantním čase.
Jakmile není na nekryté hromádce nikdo, máme cykly. Je jedno, od kterého začneme cyklus „rozmotávat“, tak si prostě jeden vrchol vezmeme a uděláme s ním to samé – řekneme, že je v záloze, toho, koho kryje, pošleme do útoku. Tím nám vznikne nekrytý hlídač (pokud měl cyklus délku alespoň 3) a pokračujeme dál obvyklým způsobem.
Dále, hromádka krytých hlídačů může být čistě virtuální – ve chvíli, kdy z ní odebíráme, tak je totožná se všemi ještě nepoužitými. A nepoužitelnost si můžeme značit přímo v hlídači a pamatovat si, kde jsme naposledy skončili s vyhledáváním.
Celkově nám z toho tedy vychází pěkná lineární složitost časová a stejně tak paměťová.
22-5-7 ArcheoPaleoLingua (Zadání)
Úkol 1: Prvočísla můžeme hledat například takto:
p N: (2=+/~Z∘.∣Z)/Z←1+ιN.
Jak toto kouzlo funguje? Nejprve si do proměnné Z uložíme čísla od 1 do N. Pak
pomocí vnějšího součinu Z∘.∣Z vytvoříme tabulku všech zbytků
po dělení a operátorem ~ ji znegujeme – výsledkem je tedy matice,
která má na pozici i,j jedničku právě tehdy, když je číslo j
dělitelné číslem i, jinak nulu. Redukcí +/ z toho vytvoříme vektor,
jehož j-tá složka udává počet dělitelů čísla j. Ten následně porovnáme
s dvojkou a dostaneme vektor, jehož j-tá složka je 1 právě tehdy,
je-li j prvočíslo. Pak už stačí použít operátor komprese, abychom
z vektoru Z získali seznam prvočísel.
Úkol 2: Úlohu si rozdělíme na dvě části: nejprve zjistíme, v jakém
pořadí se prvky mají nacházet, a pak je do něj přeházíme. Pořadí
popíšeme permutací p, což bude vektor, jehož i-tý prvek bude říkat,
na jakém místě se má objevit x[i].
Hledanou permutaci sestrojíme takto: vezmeme direktní součin x∘.<x. Ten nám
vytvoří matici nul a jedniček, jejíž i-tý sloupec prozradí, které prvky
jsou menší než x[i]. Jejich počet (zjistíme redukcí) je samozřejmě roven
místu, na kterém se má x[i] ocitnout.
Asi nejjednodušší způsob, jak pak prvky prohazovat, je využít toho,
že vektor lze indexovat vektorem, a co víc, do takto indexovaného vektoru
lze i přiřadit. Stačí tedy použít x[p]←x a je prohozeno. Celý
program vypadá takto:
x[+/x∘.<x]←x.Úkol 3: I zde, tentokrát inspirováni řešením Jirky Eichlera, přidáme jeden rozměr. Vytvoříme matici, která bude mít v každém sloupci kopii vstupního vektoru x:
y←x∘.+x×0.Také vyrobíme matici stejné velikosti s jedničkami nad diagonálou:
m←(ιρx)∘.<ιρx.
Nyní tyto jedničky přeneseme do y (m∨y) a použijeme scanování logickým součinem (∧\)
– tím pádem v i-tém sloupci zbude úsek jedniček, který se zastaví
o první nulu následující po i-tém řádku, a za ním už samé nuly.
Teď naopak všechna políčka nad diagonálou vynulujeme ((~m)∧ …). Co jsme dostali?
V i-tém sloupci bude nejprve i-1 nul, pak souvislý úsek jedniček
začínající ve vstupu na pozici i (může být i prázdný, pokud x[i]=0),
a za ním nuly. Každý maximální úsek jedniček v x se tedy vyskytuje
v alespoň jednom sloupci. Teď už stačí jedničky v každém sloupci pomocí
redukce +/ spočítat a druhou redukcí ⌈/ najít maximum:
⌈/+/(~m)∧∧\m∨y.Tím se naše okénko do prehistorie uzavírá. Co si z něj odnést do současnosti? Asi hlavně povědomí o tom, že programy můžeme budovat i z jiných základních konstrukcí než podmínek a cyklů, třeba právě z direktních součinů, redukcí a scanování. Právě tyto operace v dnešní době tvoří základ mnoha jazyků pro paralelní programování, protože se jejich provádění dá velice snadno rozdělit mezi více procesorů. Ale o tom třeba zase někdy příště.