Pátá série dvacátého druhého ročníku KSP
Celý leták v PDF.
Zadání úloh
„Je rozhodnuto, vyrazíš hned,“ zahřměl otec a skály vše zopakovaly ozvěnou.
„Ale …“
„Žádné ale!“ zaburácel, až se země zatřásla.
„…když já jsem ještě moc malý,“ pípl jsem. „Tys byl určitě větší, než
jsi odletěl.“
„Řekla to veliká pramáti a té nelze odporovat!“
„Jenže ona je netrpělivá a sklerotická. Chce mít všechno hned a zapomněla,
že jsem příliš mladý.“
„Neurážej pramáti! A teď upaluj pro princeznu.“
Jestli si myslíte, že draci mají život lehký, když umí chrlit oheň, přetrvají
věky a jsou velcí, šeredně se pletete. Téměř nikdo nás sice neohrožuje, až na
lidi, a o ty právě jde. Jsou sice drobní, jenže je jich jak mravenců. A tak se
musíme skrývat v pustých horách mezi skalami, lovit zvěř a doufat, že na nás
nepřijde armáda lučištníků.
Z bezpečí mezi štíty, tyčícími se vysoko do nebe, vycházíme jen z jediného
důvodu: ukrást si princeznu, v případě dračic samozřejmě prince. Pramáti pak
člověka očaruje tak, aby věrně sloužil svému drakovi. Princ či princezna je
vlastně celkem užitečná věc, jelikož má šikovné prťavé ručičky, což nám drakům
chybí. Navíc se jedná o tradici a zároveň rituál vstupu mezi velké draky.
22-5-1 Turnaj (10 bodů)
Ještě před odletem jsem musel dohrát turnaj v ohnivém zápase, což je
bezkontaktní souboj, v němž se postaví dva draci proti sobě a chrlí na sebe
oheň, dokud jednomu nezačne hořet tráva nandaná na čenich.
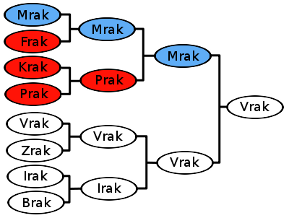
Příklad pavouka hry.
Červeně jsou
zvýrazněni ti,
které by určitě porazil drak Mrak.
Už před pár dny jsme sehráli celého pavouka vyřazovacího turnaje (dva draci se
utkají, do dalšího kola postupuje jen jeden, jenž se utká s vítězem jiného souboje …),
takže známe a obdivujeme vítěze, jenže se neumíme dohodnout, kdo je na druhém
místě. Občas totiž nelze určit, jak by dopadl souboj dvou draků, když se spolu
neutkali, nemají společného soupeře, ani jejich soupeři spolu nebojovali
a nemají společného protivníka, s nímž se utkali … Platí však alespoň
tranzitivita: jestli drak A porazil draka B a drak B draka C, porazil by i
drak A draka C.
Potřebujeme zjistit, jací jsou kandidáti na druhé místo, kolik jich je a jak mezi
nimi co nejefektivněji vybrat, tedy kolik zápasů je třeba navíc ještě sehrát. Tato
úloha je logická, takže nemusíte psát program (draci stejně nedisponují počítači),
stačí popsat a zdůvodnit postup určení druhého nejlepšího draka, který by určitě
porazil všechny ostatní kromě prvního.
Řešení
Po zdárném obhájení druhého místa jsem vyrazil. Tížil mě jen pocit, že nevím,
jestli za tohle dobrodružství nějaká princezna stojí. Ta poslední, již na
svých zádech před 100 lety přitáhl bratranec, byla podle otce nějaká podivná.
Možná si jenom na princeznu hrála. Uvidíme, jakou seženu teď.
22-5-2 Stráže údolí (10 bodů)
Nejprve jsem ovšem musel prosvištět kolem stráží hlídajících naše údolí.
Dělají nám je havrani rozmístění poblíž ústí do jiného údolí tak, aby byli na
přímce. Jenže někteří jsou moc blízko u sebe a mají tendenci se místo hlídání
vybavovat, takže jsme se rozhodli počet stráží zredukovat. Nevíme však, které
propustit.
Známe polohu všech N havranů na přímce, zadanou celočíselnými mezerami mezi
nimi, a chceme jich vyřadit K, aby byli dva nejbližší havrani od sebe co
nejdále. Potřebujeme tedy maximalizovat minimální vzdálenost mezi nimi.
Dokážete pro nás rychle najít K havranů, jež pošleme do výslužby?
Například pro N = 6, K = 3 a mezery mezi havrany 4, 6, 2, 5, 7 je
správným řešení propustit 2., 3. a 5. havrana (bráno zleva), takže zůstanou
mezery 12, 12. Pro N = 14, K = 7, mezery 5, 12, 6, 3, 8, 1, 4, 1, 1, 9,
15, 1, 16 vyhodíme 2., 4., 6., 7., 8., 9. a 12. (možností je tentokrát více).
Řešení
Hned, jak jsem přeletěl lesy, mi něco nepřišlo úplně v pořádku. Žádný drak se
totiž nikdy ve svém vyprávění nezmínil o dlouhých černých liánách vedoucích
mezi roztodivnými stromy s mnohými tenkými kmeny. Raději jsem je nadletěl.
Jakmile jsem uviděl první lidské osídlení, vlétl jsem do něj jako bouře. Tedy,
za pár desítek let už budu dost velký, abych tam vletěl jako bouře. Nicméně
jsem způsobil nemalé pozdvižení. Několik lidí sedících u stolu venku všechno
převrhlo a dalo se na zmatený únik do domu, jedna ženská zavřeštěla
„Zavolejte policií!“ (kdo je to k čertu ta policie?) a mladý pár jdoucí po
ulici se pokusil vzít přede mnou nohy na ramena.
Rozhodl jsem se dohonit prchající pár, chytl do svých spárů mladíka a pak ho
shodil na zem, aby mi neutekl. Jekot ostatních lidí nabíral na intenzitě.
„Kde najdu krále?“ zařval jsem lidským jazykem.
Kluk měl v obličeji barvu vápence, chvíli vypadal, že strachy zapomněl mluvit.
Poté, co jsem se pochlubil malým plamínkem, dokázal ze sebe vyloudit „Co
…Cože? My nemáme krále.“
„Nelži! Kde přebývá princezna?“ Nenechám se přece oblafnout nějakým zbabělcem.
Mladík na mě ještě okamžik zíral a pak ukázal na sever. „Tam …Támhle.
Velké město.“
Ještě jsem mu předvedl, že pro mě není problém zapálit celou vesnici,
a rozletěl jsem se.
Než jsem dorazil k tomu městu, setmělo se. Lidé se odjakživa báli tmy, ale
netušil jsem, že kvůli tomu rozsvěcují tolik světel. Dokonce i po cestách se
pohybovaly zářivé body, asi už dávají louče i na své koně. Mě však víc zaujala
zvláštní síť ulic.
22-5-3 Zrcadla (10 bodů)
V téhle okrajové části města byly dost podivné cesty. Tvořily totiž rozlehlou
čtvercovou síť, ale domy byly postaveny jen někde. V jednom místě se nacházel
velmi silný světelný zdroj záhadného původu svítící pouze jedním směrem.
Vzpomněl jsem si, jak mi strýc vyprávěl o zrcadlech, a napadlo mě, jestli by
se nedala využít spolu se zdrojem silného záření na osvětlení nějakého
konkrétního domu.
Je tedy dána čtvercová síť o rozměrech M×N, v níž se nachází K domů
a jeden další, na který chceme z libovolné strany dosvítit. V jednom bodě máme
světelný zdroj, který může svítit pouze vertikálně nebo horizontálně (ve smyslu
čtvercové sítě), přičemž směr si můžeme vybrat.
Ptáme se, jestli lze do čtvercové sítě rozmístit na políčka zrcadla tak, aby
byl jeden daný dům osvícen, a pokud ano, kolik nejméně jich je potřeba. Domy
jsou neprůsvitné a zrcadla umísťována do políček diagonálně (světlo se tedy
šíří po čtvercové síti vždy jen horizontálně nebo vertikálně).
Pokud například máme čtvercovou síť o rozměrech 3×3, světlo na
souřadnicích [2, 1], dům, jenž chceme osvítit, na [2, 3] a další domy na [1, 2] a
[2, 2], je správným řešením, že stačí umístit dvě zrcadla (na políčka [3, 1] a
[3, 3]).
Řešení
Stačila chvíle a vlétl jsem přímo nad moře světel. A jak byla některá silná!
To musí být ale oheň, který dokáže takhle zářit.
A ta obydlí … Mnohdy byla velmi vysoká, až se mi nechtělo letět nad ně.
I když je noc, můžou mě takhle klidně zahlédnout, říkal jsem si. Obzvlášť
v takovém velkém množství, v jakém jsou dole na náměstí.
22-5-4 Davy lidí (12 bodů)
Jak jsem se díval na stovky lidiček pod sebou, přišlo mi, že část věnuje
pozornost soše a druhá část fontáně. Navíc spousta z nich měla za objektem
svého zájmu jiného člověka tak, že socha či fontána ležela ve středu úsečky
tvořené těmito lidmi.
Mě by zajímalo, jestli se dá dav N lidí, u nichž známe jejich souřadnice
v rovině, rozdělit na dvě části, které jsou obě středově souměrné. Střed
souměrnosti jedné části tvoří fontána a střed druhé socha, ale jejich
souřadnice nejsou zadané. Někdy se čirou náhodou na fontáně či na soše může
vyskytovat člověk. Z pohledu draka jsou všichni lidé stejně body, takže jejich
rozměry zanedbejte.
Například pro 8 lidí se souřadnicemi [6, 2], [6, 4], [1, 3], [-4, -2],
[-4, 2], [1, -3], [6, -2], [6, -4] rozdělení na dvě středově souměrné
části existuje (1., 3., 4., 5., 6. a 8. člověk v jedné části, 2. a 7.
v druhé), ale 6 lidí a souřadnice [4, 0], [0, 4], [0, 2], [4, 4], [2,
3], [2, 0] už rozdělit nelze.
Řešení
Let nad městem mě už začínal docela unavovat, když jsem konečně uviděl hrad,
nebo alespoň něco jemu podobného. Každopádně jsem žádné lepší místo, kde
hledat princeznu, v okolí neviděl.
S žuchnutím jsem přistál na dlažbě a protáhl si křídla, ve vzduchu jsem byl
přeci jenom docela dlouho. Na nádvoří nikdo nebyl, takže jsem prošel branou na
další. A tam jsem ji spatřil.
Seděla na lavičce sklopená nad něčím hnědým rozlámaným na kousky a tvářila se
nešťastně. Na sobě měla dlouhý černý kabát, vysoké černé lesklé boty, což
ladilo k jejím rozpuštěným vlasům barvy temné noci s jediným červeným pruhem.
Sice prý princezny běžně vypadají jinak, ale za 100 let se lidská móda může
radikálně změnit. Popošel jsem blíže a oslovil ji.
„Milá princezno, mohu vám s něčím pomoci?“ zeptal jsem se, jak
nejgalantněji jsem uměl.
V odpověď jsem dostal škytnutí a smutný pohled. Pak vstala, popošla pár kroků
směrem ke mně, ale trochu se motala, takže se jí rozsypaly ty hnědé věci po
zemi. Zjevně jí to však nevadilo.
„Potřebuju vyřešit jeden příklad,“ říkala ztěžka. „Na zítra do školy.
Jinak ten matfyz neudělam.“
„A když ti pomůžu, poletíš na mých zádech ke mně domů?“
Podívala se na mě a zasmála se. „Jasně. Mimochodem, hustej převlek.“
„Tak povídej.“
22-5-5 Čokolámání (10 bodů)
Princezna dostala něco, čemu se říká čokoláda. Má to obdélníkový tvar a
M×N dílků, které se dají lámat podle os mezi nimi. Ke každé této ose
(horizontální i vertikální) měla napsané číslo, totiž cenu zlomu.
Její úkol spočíval v nalezení postupu, jak co nejrychleji zjistit, za jakou
nejnižší cenu lze rozlámat čokoládu na jednotlivé dílky. Cena každého zlomu
může být započítána vícekrát bez závislosti na délce zlomu. Například
rozdělíme-li čokoládu na řádky a ty pak budeme lámat, započítá se cena každého
vertikálního zlomu M krát, kdežto každého horizontálního jen jednou.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Chviličku mi úloha zabrala, ale už jsem viděl mnohem těžší. Princeznu moje
řešení zjevně nadchlo, vyskočila radostí a pak bez váhání vylezla na můj
hřbet.
„Jakého království jsi ty vlastně princezna?“ osmělil jsem se zeptat, když
přestala nadšeně vykřikovat nad úžasnou podívanou na noční Prahu, jak město
nazvala.
„Já jsem princezna …princezna …matfyzu! A tohle celé město patří jenom
nám! Podívej, támhle v těch vysokých zelených budovách sídlíme.“
Zadíval jsem se na novodobé zelené hrady a přemýšlel, jak radikálně se změnila
architektura, když tu náhle se vpravo ozval hukot. Po pár sekundách i za mnou.
A vlevo taky.
„Leť, ty můj draku, leť!“ křičela z plna hrdla moje princezna. Strach
v jejím hlase jsem však nepostřehl.
Ohlédl jsem se a uviděl spoustu zvláštních ptáků bez křídel. Všichni
vyluzovali monotónní hluk. Že by princezna měla až takovouhle ochranu proti
drakům?
22-5-6 Hlídači princezny (13 bodů)
Princezna je v království vždy velmi ceněna, a tak má spoustu bodyguardů,
strážců a hlídačů. Kdyby se všichni kryli navzájem, vznikl by akorát zmatek,
takže každý hlídač kryje právě jednoho jiného.
Do útoku proti nepříteli se vždy posílá co nejvíce hlídačů, ale každý z nich
musí být kryt někým, kdo nejde do útoku. Jak najít takové hlídače?
Úlohu si můžete představit jako orientovaný graf, kde z každého vrcholu vede
jen jedna hrana (do něj však může vést více hran, nebo žádná). Chceme najít
největší množinu vrcholů takovou, že do každého vrcholu z této množiny vede
alespoň jedna hrana z vrcholu mimo tuto množinu.
Pokud máme 5 hlídačů (očíslovaných od 1 do 5) a 1 -> (hlídá) 3, 2 -> 3,
3 -> 4, 4 -> 5 a 5 -> 3, pak vybereme do útoku hlídače 3 a 5.
Řešení
„Vyzýváme vás, abyste okamžitě sletěl dolů, jinak bude zahájena varovná
palba,“ ozvalo se silným, avšak podivně plochým hlasem zezadu.
„Vyprdni se na ně a ukaž jim, zač je toho loket!“ dodala mi odvahu moje
princezna.
„Tak se pořádně drž!“
Prudce jsem slétl dolů. Přímo mezi domy. Neztrácel jsem čas obdivováním výšky
zdejších budov a rozletěl se ulicí. Za mnou se však ozval svist hlídačů. Ihned
jsem zabočil a uslyšel obrovskou ránu. Jednomu se manévr nepodařil.
Máchal jsem křídly jako nikdy v životě, jenže oni byli pořád za mnou. Drželi
se jak klíšťata. Ještě jsem neslyšel, že by něco tak velkého dokázalo stíhat
draka.
„Prásk! Prásk! Prásk!“ ozvalo se a já pocítil bolest na levém křídle.
Provedl jsem bleskový úhyb.
„Kličkuj!“ zakřičela princezna zděšeně z hřbetu.
Nebylo třeba mě pobízet. O lučištnících jsem slyšel. Jenže tihle mají sakra
rychlé šípy.
Rychle jsem zabočil do jedné úzké uličky. „Schovej se támhle,“ zařvala
ihned. Neváhal jsem a vletěl do velkých otevřených vrat, až jsem se
bouchl jedním křídlem. Po pár sekundách kolem s hukotem prolétlo pár
princezniných strážců.
„Tak tady chvíli zůstaneme a pak rychle vyletíme.“
Byl jsem tak zadýchaný, že jsem jenom zakýval hlavou. Na vymýšlení lepšího
plánu nebyl čas.
Po několika minutách odpočinku jsme se odvážili vyjít z úkrytu. Ihned jsem
vyletěl, jak nejvýše to šlo. Naštěstí nás nezpozorovali, takže jsme se mohli
v klidu vzdálit od města a tam si odpočinout. I ona toho měla dost, hned
usnula pod mým ocasem suplujícím peřinu.
Další den jsme už naštěstí bez nepříjemných příhod dolétli domů. S princeznou
jsem nyní velmi spokojen, je chytrá, akční a šikovná. Taková dračice …
22-5-7 ArcheoPaleoLingua (14 bodů)
V této sérii si ještě jednou vyzkoušíme APL, programovací jazyk z dob
našich prababiček, pradědečků a pralidí vůbec. K základním operacím a operátorům,
které jsme si zavedli v úloze 22-4-7, doplníme pár dalších a naprogramujeme
něco krapet složitějšího. A opět bez namáčení, … totiž bez cyklů.
Dyadický operátor replikace x/y dostane dva vektory stejné délky
a vytvoří vektor, ve kterém se nejprve vyskytuje x[0] kopií prvku y[0],
pak x[1] kopií prvku y[1], atd. Tedy například 3 0 2/4 5 6 →
4 4 4 6 6. Pokud se ve vektoru x vyskytují jen nuly a jedničky, replikace
vlastně jen vybere ty prvky z y, na jejichž pozici se v x vyskytuje jednička,
tedy provede jakousi kompresi vektoru y.
Inverzní operací k této kompresi je dyadický operátor expanze x\y.
Ten na vstupu potřebuje vektor x složený z nul a jedniček a vektor y,
jehož délka je rovna počtu jedniček v x. Výsledkem je pak vektor vzniklý
z x nahrazením každé jedničky odpovídajícím prvkem z y. Kupříkladu tedy
platí 0 1 1 0 0 1\4 5 6 → 0 4 5 0 0 6 a také x/x\y → y.
Konečně přidáme operátor scanování f\x, kde f je dyadická
operace a x vektor. Dá nám vektor, jehož i-tá složka je redukce f/
prvních i+1 složek vektoru x. Nechme raději hovořit příklad:
+\1 2 3 → 1 (1+2) (1+2+3) → 1 3 6.
A nyní slíbené úkoly:
Úkol 1 (5 bodů): Napište funkci, která najde všechna prvočísla menší než dané N.
Úkol 2 (4 body): Jak v APL uspořádat daný vektor čísel vzestupně? Slibujeme,
že se žádné číslo nebude opakovat. (Zde prosíme
používejte pouze podmnožinu APL, kterou jsme nadefinovali v našem seriálu.
Operátory ⍋ a ⍒, jakkoliv krásné, se nepočítají.)
Úkol 3 (5 bodů): Je dán vektor nul a jedniček. Jak zjistit délku nejdelšího
souvislého úseku tvořeného jedničkami?
Připomínáme, že u této úlohy na časové ani paměťové složitosti nezáleží,
rozhodující je krátkost a elegance vašeho programu.
Archeologii zdar.
Řešení