Čtvrtá série dvacátého druhého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Zadání úloh

Hroch

Tentokrát se pro změnu přesouváme do daleké budoucnosti. Lidstvo dávno vymřelo, poslední člověk zmizel roku 4291. Země je osídlena roboty.

Dobrý den,
jmenuju se CPU7DR3X a jsem výzkumný robot. Mám docela štěstí, že jsem výzkumný robot. Víte, roboti se dělí do několika skupin: zásobovací roboti, výrobní roboti, výzkumní roboti, … Zásobovací roboti se starají, abychom měli vždy dostatek energie. Výrobní roboti vyrábí různé spotřebiče (a samozřejmě i další roboty). My výzkumní roboti vymýšlíme nové věci, zkoumáme planetu a její historii, zkrátka zajišťujeme přísun nových informací.

Nedávno nám opět centrála rozdělovala práci. Obvykle každému přiřazuje, co má zkoumat (samozřejmě i s termínem, do kdy se očekává slušný výsledek), ale tentokrát na mě nevyšla ŽÁDNÁ práce!! Nevím, jak se to mohlo stát, možná byla chyba v systému, nicméně měl jsem volno a chystal se toho využít. Hodlal jsem udělat nějaký velký objev, tak velký, že ani centrála by takový úkol nepřidělila, neboť by ho považovala za velmi složitý.

Zajel jsem k encyklopedii (to je takový velký počítač, ve kterém jsou uloženy všechny dosud známé informace), napojil jsem se a hledal nápady na to, co bych mohl objevit.

22-4-1 Zaheslované stránky (10 bodů)

CPU7DR3X se chce dostat na N různých stránek s důležitými informacemi. Stránky jsou naneštěstí zaheslované, na některých stránkách jsou mimo informací hesla k některým z dalších stránek. Aby se CPU7DR3X dostal na všechny stránky, potřebuje u některých prolomit bezpečnostní systém, a protože prolamování je nebezpečná činnost, chce ji provádět co možná nejméně. Úlohu mu ulehčila rada od kolegů trojských koní, kteří mu vyzradili, že ke každé stránce existuje heslo nejvýše na jedné jiné stránce.

Na vstupu dostanete seznam stránek očíslovaných 1…N a pro každou i informaci, ke kterým jiným stránkám je na ní uvedeno heslo. Napište program, který řekne, kolik nejméně stránek musí CPU7DR3X prolomit, aby si mohl přečíst informace na všech stránkách.

Strávil jsem nad tím několik hodin, ale pak jsem zjistil něco úžasného – kdysi prý na této planetě žily bytosti, které si říkaly lidé. Už podle obrázku vypadali divně, neměli žádná kolečka, žádné anténky, žádné senzory ani kamerky, ale údajně to byli jedni z nejvyspělejších historických živočichů, uměli vyrábět různé nástroje, derivovat, psát. Ale našel jsem o nich i záznamy o tom, jak poškozovali planetu – pozměnili ji natolik, že na ní už ani nedokázali žít. Bylo mi divné, že taková vyspělá zvířata jsou ohledně zachování vlastního života velmi hloupá a rozhodl jsem se, že zkusím takové zvíře zrekonstruovat. Tohle ještě nikdo nezkoušel – nejvyspělejší zvíře, které jsme dosud odchytili do laboratoře na pozorování, byl králík.

Nahrál jsem si do paměti všechny důležité informace a vyrazil jsem do terénu, abych získal podklady pro znovuoživení onoho divného zvířete. Potřeboval jsem sehnat DNA, neboť právě ona nesla veškeré informace o zvířeti.

A tak jsem se ještě toho dne vypravil hledat lidskou DNA. Napadlo mne, že nějaká by mohla být v muzeu. A tak jsem se vypravil k transportéru, který měl cestu kolem muzea, abych ušetřil pár hodin času. Během transportu jsem zaregistroval venku několik pracovních robotů hlasitě nadávajících na nezkontrolované zásilky zboží.

Řešení

22-4-2 Rozvoz zásilek (10 bodů)

Transportér je jedno velké vozidlo, převážející zboží a součástky na jednosměrné, pravidelné trase. Trasa má několik zastávek – skladišť. Transportér zastavuje na všech zastávkách v pevném pořadí daném jejich čísly – naše měkké lidské mozky si mohou představit jednu autobusovou linku.

Zboží, které se průběžně ve skladištích nakládá a vykládá, může být buď v pořádku nebo poškozené, a aby se ušetřil čas (a pracovní roboti mohli dělat jiné užitečné věci), je v transportéru zboží skener, který mezi stanicemi zásilky zboží zkontroluje a označí je, zda jsou, nebo nejsou v pořádku. Organismy založené na uhlovodících si mohou představit jakéhosi hodného revizora, který nikoho z autobusu nevyhodí, jen vás označí. Na vaší výstupní stanici si už vás „přeberou“.

Naneštěstí ne vždy je skener plně nabitý, aby mohl kontrolovat zboží mezi všemi stanicemi. Určete, jak nastavit skener (rozhodněte, mezi kterými stanicemi se skener má aktivovat), aby zkontrolovaného zboží bylo v součtu co nejvíc, když víte, že skener je nabitý natolik, že je schopen kontrolovat zboží právě N-krát.

U každé stanice znáte počet kusů naloženého zboží a počet kusů zboží transportovaného do každé z následujících stanic (z tohoto nákladu). Pozor, každý kus zboží se započítává do součtu jen jednou, i když jste ho zkontrolovali během celé cesty třeba osmkrát.

Očíslujme stanice 1…S, kde S je počet stanic. Například pro zadání (formát počet kusů:odkud->kam):

4:1->4, 2:1->2, 6:2->3, 3:2->4, 5:3->4; N = 2

je správným řešením dvojice úseků 2-3, 3-4.

Stěžování pracovních robotů mne natolik zaujalo, že jsem málem přehlédl, že už jsem u největšího biologického muzea, kam jsem se mohl během dne dostat. Největší problém bude se nenápadně dostat do muzea a opatřit si lidskou DNA. Biologické materiály v muzeu jsou střeženy a označeny jen číselnými a písmennými kódy a pro jejich získání potřebují i výzkumní roboti povolení od centrály zadávání práce, že k pokusu biologický materiál skutečně potřebují. Povolení jsem neměl, a tak jsem se musel do muzea dostat potají, najít lidskou DNA a kus jí ukrást. To rozhodně nebylo jednoduché. Kdyby na mě přišli, mohli by mě i sešrotovat! Ale v zájmu vědy …

Utěšoval jsem se, že až dokončím rekonstrukci člověka, všichni budou jásat nad mým objevem. A tak jsem se vydal k zadnímu vchodu do muzea, kudy se do něj dováží různé spotřebiče a materiály. Jelikož dovoz je častý a skoro pořád tam jezdí pracovní roboti, není to tam moc hlídané. Schoval jsem se za nedalekou bednu a pozoroval jsem zadní vchod. Za několik hodin přivezl transportér zboží a krabice. Chvíli nato vyjeli ven pracovní roboti, zboží popadli a vezli ho dovnitř. Vyjel jsem ze svého úkrytu, sebral nejbližší krabici a zamíchán mezi pracovní roboty jsem pronikl do muzea. V muzeu jsem se chodbami dostal až do výstavních míst, kde byly biologické materiály. Problém byl, že jsem neznal kód, pod kterým zde byla uchována lidská DNA.

Řešení

22-4-3 Muzeum (10 bodů)

V muzeu v biologickém oddělení se uchovává spousta biologických materiálů, které jsou tématicky roztříděny a každému tématu je vyhrazena jedna místnost. Místností je K a každá je hlídána přesně (N - 1)/K kamerami. (N je celkový počet kamer, přičemž (N - 1) je vždy dělitelné K.) Kamery jsou navzájem pospojované dráty. Navíc se v muzeu nachází centrální kamera na chodbě, z níž vede právě jeden kabel do každé místnosti, jenž je napojen na jednu z kamer. (Přes ni se pak dalšími spoji lze dostat k libovolné kameře v místnosti.) Mezi místnostmi jinak dráty vůbec nevedou.

CPU7DR3X se podařilo zjistit, jaké kamery jsou spojeny drátem. Tím získal souvislý graf oddělení (snad biologického), v němž kamery jsou vrcholy a dráty mezi nimi neorientované hrany. V tomto grafu potřebuje najít centrální kameru, tedy vrchol, z něhož vede právě jedna hrana do každé místnosti a jehož odebráním by se graf rozpadl na K komponent souvislosti. Bohužel neví, jaká kamera patří do které místnosti. Navíc si vůbec není jist, jestli se dostal do biologického oddělení, a tak zároveň potřebuje zjistit, zda je v každé místnosti (N-1)/K kamer.

Pokud například bude 10 kamer (očíslovaných od 1 do 10), 3 místnosti a spoje mezi kamerami 1-5, 2-7, 2-4, 1-10, 7-1, 4-6, 3-8, 3-7, 2-6, 8-9, má centrální kamera číslo 7 a nacházíme se skutečně v biologickém oddělení (v první místnosti jsou kamery 1, 5, 10, v druhé 2, 4, 6 a v třetí 3, 8, 9). Ovšem pro spoje 1-5, 2-7, 2-4, 1-10, 7-1, 4-6, 3-8, 3-7, 2-6, 2-9 má jedna místnost 4 kamery a jiná jen 2, takže máme graf jiného oddělení.

A tak jsem prozkoumával kamery a zjišťoval jejich počet, abych si ověřil, že jsem ve správném oddělení. Muzeum bylo obrovské, ale díky rychlému prozkoumávání kamer jsem našel správné oddělení už za 8 hodin. Zbývalo to nejdůležitější – pomalu a pracně jsem se naboural do centrálního monitoringu a vypnul jsem monitorování v celém oddělení. Pak jsem se rychle vloupal do několika vitrín, sebral kusy vzorků a prchal jsem, abych byl co nejrychleji z muzea, nejlépe ještě dřív, než přijdou na výpadek jednoho z centrálních monitoringů. Již po chvíli se strhl poplach a panika …ani si nepamatuju, jak jsem se v tom zmatku dostal z muzea. V laboratoři jsem pak vzorky pořádně prozkoumal a zjistil, že jeden z nich je opravdu lidská DNA!

Konečně jsem ho měl. Zbývalo jen to hlavní – probudit z něj k životu ono podivné zvíře. A tak jsem zajel do laboratoře. Věděl jsem, že k oživení zárodku bytosti je třeba DNA probudit k životu, ale protože u takového vyspělého zvířete to bude jistě náročné, rozhodl jsem si DNA namnožit – tak s ní budu moct dělat pokusy a vždy mi nějaká zbyde pro ty další.

A tak jsem spoustu dalších týdnů strávil tím, že jsem se snažil probudit lidskou DNA k životu. Přidával jsem k ní všechno možné, píchal do ní injekce s rozličnými látkami, pracoval s ní v různých teplotách, vlhkostech i tlacích, ale stále bezvýsledně. Teprve po několika dalších týdnech jsem v jedné ze zkumavek zaregistroval něco, co připomínalo lidský zárodek. Izoloval jsem zárodek do skleněné nádoby, vložil ho do 3D mikroskopu s největším přiblížením (jaké bylo v budově dostupné) a pořádně ho prohlédl. Nebylo pochyb – byl to skutečně lidský zárodek. Okamžitě jsem jel vložit zárodek do urychlovače – naneštěstí se přístroj zasekl a zárodek se zničil. Prohlédl jsem svoje záznamy a okamžitě jsem začal pracovat na tvorbě dalších zárodků. Zárodky jsem střídavě mutoval a ořezával, aby mi vzniklo to správné zvíře.

Řešení

22-4-4 Ořez zárodků (10 bodů)

CPU7DR3X dává zárodky v různém stupni mutace na ořezání špatných větví. Zárodek je různě rozvětvený, navíc je na něm poznamenáno místo, odkud větvení začíná.

Kdybychom měli špatný mikroskop, viděli bychom vlastně strom (souvislý graf bez kružnic) s pevně daným kořenem. Tyto stromy mají navíc jasné uspořádání synů, takže podívám-li se na některý vrchol, tak umím vždy jasně říci, který syn je první, který je druhý, a tak dále.

Není-li vám jasné, co takový strom je, podívejte se do naší Kuchařky o grafech. Ale hlubokou algebru v tom nehledejte, obrázek popisuje situaci více než dobře.

příklad: původní strom

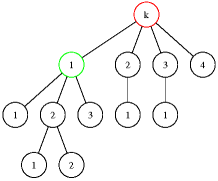
Nyní je třeba zárodek ořezat. To se udělá tak, že se nejprve vybere rozbočení (vrchol, například první syn kořene z přikladu) a v tomto místě se ještě zvolí souvislý interval synů (např. druhý až třetí syn). Původně vybrané rozbočení se prohlásí za kořen, synové kořene budou jen ty vrcholy, které byly jeho syny ve vybraném intervalu, a uspořádání se zachová (druhý syn bude prvním synem nového kořene). Spolu s tímto intervalem patří do ořezaného stromu také celé podstromy pod těmito syny. Vrcholy, které neležely v příslušném intervalu nebo byly jinde v původním stromě, v novém stromě prostě nebudou.

Naneštěstí je přístroj na ořezávání nedokonalý, takže občas oseká strom ne přesně tak, jak jsme popsali v odstavci výše. Navíc CPU7DR3X nemá v záznamech úplně pořádek a proto v nich má počáteční zárodek a ořezaný zárodek zaznamenány v nahodilém pořadí (tj. nelze předpokládat, že neořezaný je ten první). Od toho jste tu vy.

Na vstupu dostanete dva zárodky (zakořeněné stromy) a máte zjistit, jestli jeden mohl vzniknout ořezem druhého.

Stromy mohou být zadány například takto: vrcholy si očíslujeme od 1 do N, kořenem bude vrchol s číslem 1 a na vstupu dostaneme pole spojových seznamů, kde I-tý prvek pole je spojový seznam, který obsahuje číselná označení synů I-tého vrcholu, uspořádána zleva doprava. V této reprezentaci můžeme zadat „osekaný strom“ z obrázku níže například takto:

1: 2 3
2: 4 5
3:
4:
5:

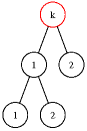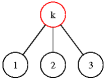osekaný strom tento z původního vzniknout nemohl

(Psst! Zaslechl jsem organizátory si šuškat o tom, že některé úlohy tohoto ročníku se dají vyřešit pomocí přiložené kuchařky o řetězcích. Tahle to ale asi nebude, že? To by bylo ujeté…váš Štek Tiskařský, v.r.)

A tak jsem dával opakovaně do urychlovače zárodky, kontroloval, zda se dobře vyvíjejí a s napětím čekal, kdy se mi konečně vyvine kompletní zvíře. Až jednou …Hurá, konečně se to povedlo! Po otevření urychlovače se v něm hýbal nějaký bledý tvor. Zvíře bylo asi metr dlouhé a obrázku ze záznamu se podobalo jen velmi hrubě. Položil jsem zvíře na podlahu. Vstalo a postavilo se na dvě úzké tyčky s klouby. (Tyto tyčky tento druh zvířat prý nazýval „nohy“.) Otočil jsem se na zvíře, připravil jsem si počítač pro záznam a zadal zvířeti jednoduchou otázku:

„Kolik je desátá derivace z x20+4x18-ex14 ·x7-x13 tg x + x(10-e5x) - sin11 x?“ Zvíře se ke mně otočilo a nepatrně se mu rozšířily hnědé kuličky na vrchní kulaté části (těmhle věcem říkala ta zvířata oči). Udělal jsem si do počítače záznam, že zvíře derivovat neumí. Popadl jsem zvíře (samozřejmě se vzpouzelo a vydávalo různé otravné zvuky) a zavezl jsem je do skladu součástek. Tam jsem zvíře pustil a (zatímco se rozhlíželo kolem) jsem mu zadal jiný jednoduchý úkol: „Vyrob solární panel!“ Zvíře se na mne notnou dobu dívalo, a pak se slabým hláskem zeptalo „Co je to solární panel?“ „Ty nevíš, co je solární panel?“ rozkřikl jsem se a udělal záznam o tom, jak je zvíře neuvěřitelně hloupé. Takovéhle bytosti že prý byly nejvyspělejší? To to tu bylo před desítkami tisíc let velmi zaostalé! Prohledal jsem svou paměť, abych si ověřil, že zvíře není příliš staré – stará zvířata byla podle záznamů mnohem blbější než mladá. Zvířata začínala podle záznamů blbnout stářím asi kolem 70ti let. Otočil jsem se na zvíře a zeptal jsem se „Kolik je ti let?“ Zvíře odpovědělo: „Je mi pět let.“ Tady něco nehrálo. Zvíře nebylo staré a přesto nefungovalo tak, jak by podle záznamů fungovat mělo. Po projití dat v paměti jsem si připomněl, že příliš mladá zvířata toho také moc neumí. Přes protesty a pohyby zvířete jsem je popadl a odvezl je do urychlovače. Potřeboval jsem, aby bylo o něco starší. Dal jsem zvíře do urychlovače, zaklapl víko a přes jeho vřeštění jsem přístroj zapl. Řev slábl a když na přístroji zasvítily kontrolky, otevřel jsem urychlovač. Zvíře se ohnulo v půlce, slezlo z urychlovače a já mu opět položil otázku: „Kolik ti je let?“

Tentokrát zvíře odpovědělo: „Je mi třiadvacet …“ Zadal jsem mu opět jednoduchý příklad na derivování. Tentokrát zvíře chtělo něco na psaní. Ukázal jsem mu zastaralý model počítače, který se často sekal (přeci jen, nemohu riskovat, že by zvíře zničilo nějaký drahý přístroj), zvíře se uvelebilo před obrazovkou, zmáčklo tlačítko, ale starý počítač se nenastartoval. Co to? Po bližším zkoumání se ukázalo, že v počítači nebyl energetický článek. Otevřel jsem zásobník článků a začal uvažovat, který dát do počítače.

Řešení

22-4-5 Energetické články (10 bodů)

CPU7DR3X otevřel zásobník, ve kterém je N různých druhů energetických článků. Každý článek se vyznačuje tím, že je souměrný vzhledem k tomu, z jakých částic se skládá. (Např. RAR je energetický článek, RAN není energetický článek. My neroboti říkáme, že článek je palindromem.) Články lze spojovat, ale jen tehdy, pokud vzniklý článek je opět souměrný. CPU7DR3X chce vložit do počítače článek složený ze dvou článků a zajímá ho, z kolika různých příslušných uspořádaných dvojic článků si může vybrat.

Na vstupu dostanete N různých článků, zadaných slovním schématem (N slov, palindromů). Vaším úkolem je napsat program, který spočítá, kolik uspořádaných dvojic (dvojici přečteme jako jedno slovo zleva doprava) opět tvoří energetický článek (palindrom).

Například dvojice (RAR, ARA) palindrom netvoří, ale dvojice (BAB, BABBAB) palindrom tvoří.

Tato úloha je praktická a řeší se ve vyhodnocovacím systému CodEx. Pokud jste zatím žádnou praktickou úlohu neřešili, přečtěte si stručný úvod zde.

Po úspěšném zapojení počítače začlo zvíře konečně počítat příklad. Přitom se mnou mluvilo a kladlo spoustu otázek – zjevně se mu okolní prostředí líbilo a zajímalo ho. Udělal jsem si záznam, že ve 23 letech zvíře derivovat umí a právě jsem si chtěl zapsat, jak dlouho mu to trvá, když se rozletěly dveře a dovnitř vjelo a vlétlo několik masivních bezpečnostních robotů. Někteří mne popadli a někam mne odváželi (a dočasně mi vyzkratovali kamerky), poslední co jsem zahlédl bylo, že ostatní se vrhli na zrekonstruované pokusné zvíře.

Když jsem konečně mohl vnímat obraz, byl jsem znehybněn uprostřed malé místnosti a okolo mne bylo asi osm robotů, kteří na mne přísně shlíželi. Jeden z nich popojel ke mně a řekl: „CPU7DR3X, toto je tvůj soud za ohrožení bezpečnosti všech robotů!!“ Zeptal jsem se, co jsem provedl. A ten robot popojel ještě o kousíček blíž, až jsem se bál, že do mne nabourá, a zahřímal: „Cos provedl?! Ohrozil jsi celou naši existenci obnovením velmi nebezpečného druhu!“ Nechápal jsem, jak by nám jeden člověk mohl být nebezpečný a obhajoval jsem se, že jsem učinil významný objev, ale nic mi nevysvětlovali a odešli do vedlejší místnosti se radit, jak mne potrestají.

Přemýšlel jsem o tom, jak se dozvěděli, že jsem vyrobil člověka, a vzpomněl jsem si, že mezi roboty již dlouho kolují nepodložené informace, že všechny činnosti robotů pozoruje jakési Tajné Bratrstvo, které má všude rozmístěny skryté kamery (a které tudíž muselo hned zaznamenat, že jsem odpojil centrální monitoring v muzeu). Nikdy jsem těmto zkazkům nevěřil – až dnes jsem se přesvědčil, že jsou pravdivé.

Když se Bratrstvo vrátilo, oznámil mi jeden z nich, že s konečnou platností přestávám být výzkumným robotem a přeřazuji se mezi roboty pracovní. Pak mne převezli do laboratoře, kde mi z paměti vymazali všechna hesla a přístupové kódy do místností sloužících k výzkumu, sběru informací, prostě do místností informačního a výzkumného charakteru. A tak jsem teď jen pracovním robotem. Pracovním robotem té nejnižší kategorie.

Řešení

22-4-6 Umisťování panelů (13 bodů)

CPU7DR3X byl přeřazen mezi nejnedůvěryhodnější pracovní roboty. Nyní místo výzkumu bude s ještě jedním pracovním robotem umisťovat na louku panely pro příjem větrné a sluneční energie. Louka je rozdělena pomocí kolíků na čtvercovou síť (kolíky jsou v rozích čtverců), v některých čtvercích mají být umístěny panely (jeden nebo i více). Na louce má být celkem umístěno N panelů. Na louce budou stavět panely dva nedůvěryhodní roboti, z nichž každý má postavit K panelů. A protože ti dva pracovní roboti jsou nedůvěryhodní, je potřeba v rámci zabezpečení nalézt pro každého z nich obdélníkový prostor, kde má být celkem postaveno K panelů a tyto prostory ohraničit z kolíků bezpečnostními paprsky. Jelikož na paprsky je potřeba energie v závislosti na délce paprsku (kterou se pokud možno šetří), má součet obvodů vytyčených pracovních míst být co nejmenší. Oba pracovní prostory se navíc nesmějí překrývat a pokud někde mají společnou hranu, je stejně potřeba v tomto místě vést paprsek pro každou pracovní plochu zvlášť (tj. v takové hraně budou dva paprsky).

Na vstupu dostanete na prvním řádku rozměry louky (délka a šířka), na dalším čísla N a K, a na dalších N řádcích dostanete souřadnice pro umístění jednotlivých panelů (délka a šířka) – na každém řádku jeden. Napište program, který vypíše minimální počet jednotek (jednotka – mezi dvěma kolíky) paprsků, které jsou potřeba k ohraničení dvou disjunktních obdélníkových pracovišť (z nichž na každém má být dle plánu K panelů) nebo vypíše, že pro příslušná data řešení neexistuje.

Bodování:

Nevím, co udělali s člověkem, ale nejspíš ho rozebrali. To je mi moc líto, takový velký objev jsem učinil a nikdo to neocení. Když mě propouštěli ze soudní místnosti, jeden z nich mi dokonce pošeptal „Máš štěstí, moh jsi skončit ve šrotu …“

Řešení

22-4-7 Pozdrav z pravěku (12 bodů)

Láká vás podívat se na programovací jazyk z dob, kdy muži byli ještě praví muži, ženy pravé ženy a počítače praví mamuti, aspoň co do velikosti? Jazyk, v němž opravdoví programátoři píší programy jen tehdy, když se vejdou na jeden řádek, což je ovšem překvapivě často? Jazyk, který má tolik jednoznakových příkazů, že by se na psaní všech těch znaků hodila klaviatura od varhan? Pak jste na správné adrese, protože dnes si budeme povídat o jazyku APL.

Historie APL se začala psát v roce 1964, kdy Kenneth Iverson dumal nad tím, proč chce-li něco jednoduchého spočítat, musí kvůli tomu psát složitý program, když přitom celý výpočet lze příjemně a stručně popsat matematickou notací. Chvíli experimentoval, až napsal interpreter jazyka založeného právě na matematické notaci a k tomu knížku s prostým názvem A Programming Language. A APL bylo na světě. Pojďme si ukázat pár jeho nejdůležitějších vlastností a zkusit si v něm zaprogramovat. Mezi řečí občas potkáte jednoduché úkoly, tentokrát po vás budeme chtít, abyste vymysleli co nejelegantnější (zejména co nejkratší) řešení bez ohledu na časovou složitost.

Předně bychom měli vědět, že APL je interaktivní – když mu napíšete výraz, interpreter ho ihned vyhodnotí a vypíše vám výsledek (v dnešní době nic moc překvapivého, ale v době dřevěných počítačů …). Třeba na 1+2+4+8 vypíše 15, na 3*6 vypíše poněkud nečekaně 729, protože * značí umocňování, kdežto násobení se značí ×. Tedy 3×6 je 18. I ostatní operace se píší trochu nezvykle: dělení je ÷, zbytek po dělení ∣ (pozor, má opačně argumenty, takže 3∣7 = 7 mod 3 = 1). Ještě nás asi překvapí, že 3×4+1 = 15, protože neexistují priority operací a vše se striktně vyhodnocuje zprava doleva, pokud neurčíte jinak závorkami.

Většina operací existuje ve dvou formách: dyadické (ty chtějí dva argumenty, dneska bychom jim asi spíš říkali binární) a monadické (žádají jeden argument, jinak též unární). Obvykle obě formy počítají něco podobného: například dyadické x÷y dělí a monadické ÷y počítá převrácenou hodnotu. Celý zvěřinec aritmetických operací vypadá takto:

x+y sčítání +x identita (vrací x)
x-y odčítání -x otočení znaménka
x×y násobení ×x signum (viz níže)
x÷y dělení ÷x 1/x
x∣y y mod x, 0∣x=x ∣ x absolutní hodnota
x⌈y maximum ⌈x horní celá část
x⌊y minimum ⌊x dolní celá část

Operace ×x vrátí jedničku pro kladné x, -1 pro záporné x a nula od nuly pojde.

Logické operace se zapisují jako v matematice, přičemž na vstupu považují 0 za nepravdu a cokoliv nenulového za pravdu; na výstupu dávají vždy 0 nebo 1. Podobně při porovnávání čísel dostanete vždy výsledek 0 nebo 1:

x∨y nebo x<y menší než
x∧y a zároveň x>y větší než
~x negace x≤y menší nebo rovno
x=y rovnost x≥y větší nebo rovno
x≠y nerovnost

Přiřazení funguje, jak čekáte, a značí se šipkou: x←5 přiřadí do proměnné x hodnotu 5. Příjemné je, že se chová jako funkce a vrací hodnotu, kterou přiřadilo, takže můžeme psát (podobně jako třeba v Céčku) x←y←5.

Můžete si také definovat vlastní operace. Nejjednodušší je to pro monadické: f x: x*2 zavede monadickou operaci f, která vrátí druhou mocninu svého parametru. Kdybychom chtěli definovat dyadickou operaci g, řekněme pro součet druhých mocnin, napíšeme x g y: (f x) + (f y). Funkce více parametrů dostávají parametry ve složených závorkách oddělené středníky: max{a;b;c}: a⌈b⌈c.

Úkol 1 (1 bod): Nadefinujte operaci ×x (signum) pomocí ostatních operací.

APL je vektorové – v podstatě všechno, co umí provádět s čísly, dokáže i s posloupnostmi čísel (čili vektory). Například 1 2 4 + 3 1 2 sečte vektory 1 2 4 a 3 1 2 po prvcích, takže vyjde 4 3 6. Pokud k vektoru přičítáme konstantu, přičte se ke každému prvku: 1 2 4 + 1 → 2 3 5. (Zde raději místo rovnítka značíme výsledek šípkou, protože = by se jako každá jiná operace na vektory aplikovalo po prvcích.) Obecně to funguje takto: Pokud použijeme na vektor monadickou operaci, provede se s každým prvkem zvlášť. Použijeme-li dyadickou na dva stejně dlouhé vektory, provede se po prvcích (první s prvním, druhý s druhým atd.). Pokud dyadickou na vektor a číslo, z čísla se vyrobí vektor tím, že se číslo zopakuje.

Často potřebujeme vyrobit vektor čísel 0,… ,n-1. Tehdy se hodí operátor ιn (iota), který přesně takové vektory vytváří.

Mimo vektorů APL dokáže pracovat i s vícerozměrnými poli: ι a b c vytvoří trojrozměrné pole velikosti a×b×c a vyplní ho čísly od 0 do (a×b ×c)-1. Obecně můžete operátoru ι dát jako parametr libovolný vektor a on vás obdaří polem, které má tolik rozměrů, kolik je délka vektoru, přičemž každá složka určuje, jak je pole v daném rozměru velké. Počtu rozměrů se říká rank pole. Dvojrozměrným polím budeme říkat matice.

Úkol 2 (1 bod): Co udělá ι5+1 a co 1+ι5? (Nezapomeňte, v jakém pořadí se vyhodnocují operace.)

Úkol 3 (1 bod): Co udělá ι(2+ι3)?

Pokud chceme zjistit, jak je nějaké pole velké, stačí použít monadický operátor ρ (ró). Ten vrátí vektor, jehož jednotlivé složky jsou velikosti v jednotlivých rozměrech. Tedy ρι2 3 4 vrátí 2 3 4. Je-li x vektor, ρx musí tedy být jedno číslo, které udává počet prvků vektoru. Proto ρρp vrátí rank pole p.

Ještě jsme ale nepřišli na to, jak vícerozměrné pole zadat. K tomu se hodí dyadická forma operace ρ. Ta slouží k přeformátování pole na dané rozměry: 2 3 ρ 4 5 6 7 8 9 například vezme vektor 4… 9 a přerovná ho na matici o dvou řádcích 4 5 6 a 7 8 9. Pokud má původní pole příliš málo prvků, začnou se opakovat: 2 3 ρ 1 2 vyrobí matici s řádky 1 2 1 a 2 1 2. Přerovnávání přitom zachovává standardní pořadí prvků: vektor se čte zleva doprava, matice se čte po řádcích, vícerozměrné tak, že se první rozměr mění nejpomaleji a poslední nejrychleji.

Pole můžeme také indexovat (od nuly): pokud je x vektor, pak x[0] je jeho nultý prvek, x[1] první atd. Jako index můžeme také použít vektor, v tom případě vybereme více prvků najednou: x[0 2 3] dá vektor skládající se z prvků x[0] x[2] x[3]. U vícerozměrných polí se indexy oddělují středníkem: y[1;3] je třetí prvek na prvním řádku matice y, y[2 3;2 3] je čtvercová podmatice 2×2 „vykousnutá“ z matice y. Na pole ranku k se také můžeme dívat jako na vektor, jehož prvky jsou pole ranku k-1, tedy pro matici y je y[0] její první řádek, y[1] druhý atd.

Existuje řada dalších operací, které zacházejí s vektory. Zajímavé je třeba spojování vektorů za sebe nebo pod sebe. Spojení za sebe se zapisuje čárkou: x,y je vektor, který obsahuje nejprve všechny prvky vektoru x a pak všechny prvky z y. Spojení pod sebe neboli laminace x~y má za výsledek dvojřádkovou matici, jejiž prvním řádkem je vektor x a druhým vektor y (řádky přitom musí být stejně dlouhé). Obě operace samozřejmě fungují i na vícerozměrná pole: čárka spojuje v prvním z rozměrů (matice tedy slepuje pod sebe), laminace přidá na začátek nový rozměr, takže (x~y)[0]→x a (x~y)[1]→y.

Hodit se nám bude též redukce +/x. Ta spočte pro vektor x=x0 x1 … xn-1 výraz x0+x1+… +xn-1, tedy součet všech prvků. Podobně můžete pomocí lomítka vyrobit z nějaké operace její redukční verzi zpracovávající postupně prvky vektoru: například ⌈/x vrátí maximum z vektoru.

U vícerozměrných polí se redukce chová trochu záludněji. Pokud použijeme +/ například na matici, což, jak už víme, je vektor řádkových vektorů, sečte nám jednotlivé řádky, takže vznikne vektor, jehož i-tá složka vyjadřuje součet i-tého sloupce matice. Třeba pro matici

x=ι3 4 =
( 0123 )
4567
891011

spočítáme +/x → (0 1 2 3)+(4 5 6 7)+(8 9 10 11) → 12 15 18 21.

Co kdybychom naopak chtěli sčítat prvky v každém řádku? Tehdy je nejjednodušší použít operaci transpozice ⍉, která prohodí obě souřadnice – řádky se nyní stanou sloupci a naopak. Pro řádkové součty tedy stačí +/⍉x.

Úkol 4 (1 bod): Jak spočítat maximum ze všech prvků matice?

Na lomítko se můžeme dívat jako na něco, co dostane dyadickou operaci s čísly a vyrobí z ní monadickou operaci s vektory (nebo obecněji z dyadické operace s poli ranku k vyrobí monadickou operaci s polem ranku k+1). Takových konstrukcí, které vyrábějí z operací jiné operace, má APL víc a říká se jim operátory.

Dalším důležitým operátorem je direktní součin ∘.f, kde f je nějaká dyadická operace. Pokud ho použijeme na vektory x a y (tedy napíšeme x∘.fy), dostaneme matici, jejíž prvek na pozici (i,j) obsahuje výsledek operace f aplikované na i-tý prvek vektoru x a j-tý prvek vektoru y. Výraz (ι10)∘.×(ι10) nám tedy vytiskne malou násobilku. Direktní součiny samozřejmě fungují i s poli vyšších ranků; snadno si domyslíte, jak, když napovíme, že součinem pole ranku k s polem ranku ℓ bude pole ranku k+ℓ.

Potkali jsme tedy zatím tyto operace pracující s poli:

ιn iota: generátor přirozených čísel
ρx zjištění rozměrů pole
xρy přeformátování pole y na rozměry x
x[...] indexování pole
⍉x transpozice (překlopení)
x,y spojení za sebe
x~y laminace (spojení pod sebe)
f/x operátor redukce
x∘.fy operátor direktního součinu

S prohlídkou dalších operací a operátorů počkáme do příště, i s těmi, co už známe, se dá naprogramovat ledacos:

Úkol 5 (2 body): Napište funkci, která vytvoří matici n×n z nul a jedniček, která bude mít na i-tém řádku i jedniček a za nimi n-i nul.

Úkol 6 (3 body): Jak pro dané sudé n vyrobit vektor 0, n-1, 1, n-2, 2, n-3, … , n-1, 0?

Úkol 7 (3 body): Vymyslete, jak v APL spočítat největšího společného dělitele dvou čísel.

Ještě dodejme, že jde vytvářet i delší programy – stačí napsat více řádků a na každém jeden výraz, nebo případně více výrazů na řádek oddělených středníkem. Pokud byste si chtěli APL vyzkoušet, mohlo by se vám hodit:

Pokud se vám nechce nic instalovat, můžete samozřejmě psát programy na papír a nemajíce varhany, psát místo podivných znaků jejich názvy.

APL a dnešní doba. Masového rozšíření se APL nikdy nedočkalo (snad proto, že jen opravdovým programátorům vyhovuje programovat tak, že hodinu se zavřenýma očima přemýšlejí, načež si sednou k počítači a napíší jednořádkový program). Přesto ale není pouze mrtvým jazykem vystaveným v muzeu počítačové prehistorie – stále vznikají nové implementace APL (například A+ nebo dokonce APL.Net) a jazyky od APL odvozené (třeba jazyk J, který se snaží vystačit si bez varhan, tedy se znaky na běžné klávesnici). Navíc se s nástupem víceprocesorových počítačů ukazuje, že programy skládané pomocí vektorových operací a operátorů, jako je třeba naše redukce a direktní součin, jsou velice dobře paralelizovatelné. Kdo ví, co se ještě o APL naučíme.

Řešení