Třetí série dvacátého třetího ročníku KSP
Celý leták v PDF.
Zadání úloh
Edsger Dijkstra byl slavný holandský myslitel. Byl to samotářský,
konzervativní člověk, kterému se jen velmi těžko určuje obor, jímž se zabýval.
Narodil se roku 1930 v Rotterdamu, kde zůstal až do svých vysokoškolských
studií teoretické fyziky. Později žil a učil v Eindhovenu, kde se věnoval
praktické i teoretické matematice a informatice.
Zabýval se mimo jiné i grafy. Jedním z nejznámějších algoritmů, které vymyslel,
je hledání nejkratší cesty v ohodnoceném grafu, jenž po něm nese jméno a můžete
si ho přečíst třeba v naší
kuchařce. My bychom po vás
teď chtěli vymyslet jeden trochu jednodušší, ale zdánlivě podobný algoritmus.
23-3-1 Úsporný kořen (9 bodů)
Na vstupu dostanete
neohodnocený strom zadaný
počtem vrcholů a seznamem hran. Vrchol s hloubkou x bude takový vrchol, od
kterého je každý jiný vrchol vzdálený maximálně x. Úsporný kořen je vrchol
s nejmenší možnou hloubkou. Nalezněte všechny úsporné kořeny stromu.
Příklad vstupu:
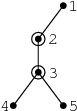
5
1 2
2 3
3 4
3 5
Výstup: 2 3
Řešení
Jako správný samotář bydlel na vesnici, takže do školy jezdil jen v úterý. Vedl
tam i seminář, kterému se příhodně říkalo Tuesday Afternoon Club, kde se řešily
úlohy podobné těm z KSP. Kdykoliv tam či jinde studenti příliš hlasitě šuškali
(to asi dobře znáte), nekřičel, ale naopak začal šeptat. To mělo ohromný efekt
– všichni ztichli. Takový měl respekt.
Když se později stěhoval do Ameriky a cesta mu připadala dlouhá, vymyslel
úlohu, kterou pak zadal americkým studentům při jejich prvním semináři
Tuesday Afternoon Club.
23-3-2 Nejkratší cesta přes oceán (14 bodů)
 Pro zjednodušení si severní Ameriku i Evropu představme jako dva
konvexní n-úhelníky, které se neprotínají. Chcete nalézt nejkratší cestu mezi
nimi. Na vstupu nejdříve dostanete souřadnice Ameriky a potom souřadnice Evropy
jako vrcholy v pořadí, v jakém leží na obvodu.
Pro zjednodušení si severní Ameriku i Evropu představme jako dva
konvexní n-úhelníky, které se neprotínají. Chcete nalézt nejkratší cestu mezi
nimi. Na vstupu nejdříve dostanete souřadnice Ameriky a potom souřadnice Evropy
jako vrcholy v pořadí, v jakém leží na obvodu.
Vaším úkolem je najít takové dva
body, jeden na obvodu Ameriky a druhý na obvodu Evropy, aby jejich vzdálenost
byla co nejmenší. Pokud je víc možností, stačí vypsat libovolnou z nich.
Vstup (znázorněný obrázkem):
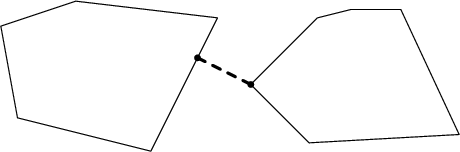
5
0 75
10 20
90 0
130 80
45 90
6
185 5
275 10
240 85
210 85
190 80
150 40
Výstup (čárkovaně):
118 56
150 40
Řešení
Krom tisíce jiných věcí přemýšlel, jak počítače naučit počítat, třeba
odpovědět na zadání
1+2*3. K tomu účelu znovu objevil postfixový zápis a
objevil, jak na něj běžný infixový zápis rychle převést. Pokud to chcete umět
taky, můžete se podívat třeba do
Wikipedie.
Abychom nezůstali jen u teorie, podílel se na vývoji programovacího jazyka
ALGOL 60 a později i jeho prvního překladače. Tento jazyk vznikl pro snadný zápis
algoritmů a jako konkurence tehdy mohutně nasazovaného BASICu.
Edsger Dijkstra vůbec velmi brojil proti příkazu goto a zasazoval se
o strukturované programování. Příkaz goto považoval za nepřehledný.
Samozřejmě, že na úrovni procesoru se stále používá, ale programátor by od něj
měl být odstíněn, pokud to jen jde.
Měl rád programování rovnou na čisto, nejdřív si program rozmyslet a pak jej
plynule psát. Lepší je chyby nedělat, než je hledat.
Následující úlohu vymyslete rovnou bez chyb a tak, aby šla zapsat bez goto.
Pokud nevíte, co to goto je, máte to snazší, buďte jen rádi.
23-3-3 Skok bez padáku (13 bodů)
Z letadla vyskočil Američan, leč až po výskoku si uvědomil, že místo padáku si
vzal batoh spolucestujícího Čecha. Naštěstí pro něj je na stráni pod ním
rozmístěno N trampolín.
Představme si stráň jako rovinu postavenou svisle, tedy souřadnice x
určuje horizontální pozici a souřadnice y je výška.
Každá trampolína je určena dvojicí souřadnic (x,y). Parašutista má nějakou
počáteční pozici (x0, y0). Padá ve směru osy y, dokud nenarazí na
trampolínu, která je o d níže než on. Od ní se odrazí a vyletí o d/2 výše,
pak si může vybrat, jestli se posune o 1 vlevo, nebo vpravo (posunout se
musí) a posune se podle toho.
Toto se opakuje, dokud nedopadne na zem. Na vstupu také dostanete výšku h;
pokud spadne na zem z větší výšky, způsobí si zranění neslučitelná se životem
a přivolaný lékař konstatuje smrt.
- Určete, jestli má šanci přežít, a pokud ano, jak má postupovat. Nalezněte nejkratší možné řešení (nejméně odrazů). (5 bodů)
- Nalezněte všechna možná y≤ y0, pro která přežije pád s počáteční pozicí (x0,y). (8 bodů)

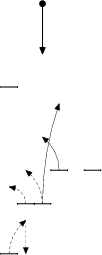 Příklad vstupu: Na prvním řádku jeho počáteční souřadnice a h0,
na druhém řádku K, na dalších K souřadnice trampolín.
Příklad vstupu: Na prvním řádku jeho počáteční souřadnice a h0,
na druhém řádku K, na dalších K souřadnice trampolín.
Na obrázku vlevo náčrt zadání, vpravo možné řešení (nejprve skáče po plných,
následně po čárkovaných šipkách).
2 15 3
6
0 0
0 10
1 3
2 3
3 5
5 5
Řešení
Zasazoval se o eleganci nejen zdrojových kódů, ale i matematických důkazů. Ty
jeho byly zvlášť pěkné. Málokdy přesáhly 16 stran a každou větu pečlivě
vybíral, aby nebyla zbytečná, nudná ani nepochopitelná. Důkazy psal jako
pohádky. Neměl rád dlouhé formální řady implikací ani důkazy sporem, zato
zvládl i třeba v geometrii nebo algebře použít algoritmické důkazy a jiné
překvapivé finty z programátorského světa.
Třeba tohle je pěkný důkaz.
Jeho konzervativní přístup k vědě se projevoval třeba tím, že nerad jezdil na
konference, ale raději vykládal v menší skupině lidí. Většinu své práce psal na
stroji. Osobní počítač si pořídil až ke konci života, ale i tehdy ho používal
minimálně a preferoval psaní rukou. Měl krásné technické tiskací písmo, které
se používá i jako počítačový font.
23-3-4 Psaní písmen (10 bodů)
 Každé písmeno se skládá z bodů a linií, které je spojují. V jednom bodě
může začínat i končit více linií. Při psaní perem lze psát víc navazujících
linií jedním tahem, nejde-li to, musí se pero zvednout a začít jinde. Kolikrát
nejméně je potřeba pero zvednout?
Každé písmeno se skládá z bodů a linií, které je spojují. V jednom bodě
může začínat i končit více linií. Při psaní perem lze psát víc navazujících
linií jedním tahem, nejde-li to, musí se pero zvednout a začít jinde. Kolikrát
nejméně je potřeba pero zvednout?
Na vstupu dostanete neorientovaný graf
o N vrcholech a M hranách a vypište, kolika nejméně tahy lze nakreslit.
Samozřejmě šetříme, takže je zakázáno jakoukoli hranu nakreslit více než
jednou. Jinak řečeno, nesmíte se vracet po již nakreslených liniích.
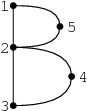 Příklad vstupu:
Příklad vstupu:
5 6
1 2
2 3
3 4
4 2
2 5
5 1
výstup: 1
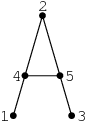 Jiný příklad:
Jiný příklad:
5 5
1 4
4 2
2 5
5 3
4 5
výstup: 2
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Jeden z mnoha jeho textů (EWD 1250) – známý problém dvou párů, loďky a řeky. K řece
přišly dva páry a potřebují překonat řeku tak, aby nikdy nezůstal sám pán
z jednoho páru s dámou z druhého páru. Loďka unese maximálně dva lidi.
Pamatoval i na ty, kteří už úlohu znali, nebo hned vyřešili.
„Žádost:
Pokud vám připadá tento problém příliš jednoduchý na to, abyste na něj plýtvali
svým časem, hledejte prosím místo toho počet různých řešení. Děkuji.
⟨Konec žádosti.
⟩“
Mimochodem, někteří organizátoři KSP mají velmi podobné písmo… také vám
připadá výrazně čitelnější než klasické psací písmo?
Někdy mu bylo vyčitáno, že neuváděl žádné nebo málo zdrojů. Ale co měl dělat,
když něco vymyslel jen tak? Navíc většinu své práce nepublikoval v časopisech,
ale posílal přátelům a známým. Tyto články jsou označovány EWD (jeho
iniciálami) a číslem, třeba EWD 1250, a dají se stáhnout
volně na internetu.
Analogii můžeme najít v hudbě, kde se takhle označují díla slavných
skladatelů, asi nejznámější jsou BWV (Bach-Werke-Verzeichnis) a
HWV (Händel-Werke-Verzeichnis). Zásadní rozdíl je ovšem, že Dijkstra si to
čísloval sám, kdežto hudebníci to neřešili a udělal to za ně někdo jiný
o mnoho let později.
EWD shromažďuje pan Ham Richards. Jednou, když je nesl, zakopl a rozsypaly se
mu po podlaze.
23-3-5 Rozházené EWD (7 bodů)
 Chudák pan Richards má jen svou zapomětlivou hlavu a pár papírů, tak budete
muset vymyslet, jak setřídit EWD v konstantní paměti. To jest, že si může
udělat třeba 1000 záznamů, ale ne pro každou z N EWD jeden. Vámi spotřebovaná
paměť prostě na N vůbec nesmí záviset (a N může být libovolně velké –
argument, že EWD je konečně mnoho, vám neprojde). Dávejte si pozor na rekurzi,
spotřebovává tolik paměti, jak hluboko je zanořená.
Chudák pan Richards má jen svou zapomětlivou hlavu a pár papírů, tak budete
muset vymyslet, jak setřídit EWD v konstantní paměti. To jest, že si může
udělat třeba 1000 záznamů, ale ne pro každou z N EWD jeden. Vámi spotřebovaná
paměť prostě na N vůbec nesmí záviset (a N může být libovolně velké –
argument, že EWD je konečně mnoho, vám neprojde). Dávejte si pozor na rekurzi,
spotřebovává tolik paměti, jak hluboko je zanořená.
Přeházená EWD budeme reprezentovat jako spojový seznam. V programu dostanete
ukazatel na první prvek spojového seznamu, kde je číslo EWD a ukazatel na
další. Vaším úkolem je ho setřídit a vrátit ukazatel na první prvek (nejstarší
EWD).
Spojový seznam už máte v paměti, vaším úkolem je přepojit jej do setříděného stavu.
Příklad před setříděním:
A po setřídění:
Řešení
Z úplně jiného soudku je jeho návrh operačního systému THE multiprogramming
system, zaměřeného na sekvenční zpracování úloh a s podporou multitaskingu a
paralelizace. Velkého rozšíření se sice nedočkal, nicméně myšlenky vytvořené
pro něj se ujaly. Jestli vás paralelní svět zajímá, měli jsme o něm kdysi
seriál a také o něm byla série úloh
před pár lety v Matematické olympiádě.
Jako už starý se vrátil do Holandska do svého původního domu ve vesnici Nuen, kde
roku 2002 zemřel na rakovinu.
Pozůstalí pak přemýšleli, jestli mu na hrob napsat, že byl matematik, nebo informatik.
Hodilo by se jim k rozhodování vědět, kolik procent lidí si nejčastěji myslelo, že
byl informatik.
23-3-6 Výzkum veřejného mínění (9 bodů)
Za jeho života se dělalo N výzkumů veřejného mínění, jestli byl
informatik. Výsledkem bylo vždy číslo v procentech s přesností na M
desetinných míst. N je řádově tolik jako 2M. Můžeme předpokládat, že
výzkumy odpovídaly realitě a mezi jednotlivými výzkumy procento lidí, kteří si myslí, že ano, buď
jen stoupalo, nebo jen klesalo. Vaším úkolem je zjistit, jaké procento bylo
během jeho života nejčastější. Případně určit libovolné z nejčastějších.
Nezapomeňte, že to nutně nemuselo být v době, kdy se konal výzkum.
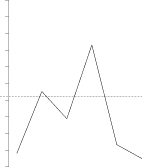 Příklad vstupu:
Příklad vstupu:
6 5
8.124 45.223 28.8723 73.117 13.3 5.0
Výstup (vyznačen čárkovanou čarou): 42.42 (4×)
Řešení
23-3-7 Automaty stokrát jinak (12 bodů)
 Tento text navazuje na předchozí dvě série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
Tento text navazuje na předchozí dvě série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
Minule jsme si popsali nedeterministický konečný automat (NKA)
s ε-přechody. Definovali jsme, že vstup přijme, pokud v něm existuje
alespoň jedna možnost, jak při čtení onoho vstupu skončit ve výstupním stavu.
Běžný program ale neumožňuje paralelně zkoumat všechny větve, kterými by mohl
procházet. To bychom si museli pořídit třeba paralelizátor jako v jednom ze
starých ročníků olympiády.
Mohli bychom však zkusit převést NKA na DKA, který programem simulovat velmi
jednoduše umíme. Dá se dokázat, že to jde vždycky (i když výsledný automat
může mít až exponenciální velikost), ale obvykle se to dělá ukázáním obecného
postupu, takže si to ukážeme až v řešení.
Úkol 1 [6b]
Vymyslete, jak simulovat NKA a jak převést NKA na DKA. Pokud vám to
nepůjde ve vší obecnosti, máte šanci získat 2 body za převod tohoto
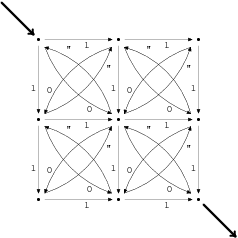
konkrétního automatu:
Samozřejmě, pokud vymyslíte úlohu obecně, tak ji nemusíte řešit konkrétně na
tomto automatu, nicméně snad nic nebrání jeho použití třeba k názornému
ilustrování vašeho postupu.
Za pomoci mašinérie, kterou jsme si zatím ukázali, by pro vás neměl být
problém zjistit následující (ale můžete to dělat i jinak, jestli chcete):
Úkol 2 [5b]
Zjistěte, jestli tyto dva regexy popisují stejný jazyk (tedy vyhovují
jim právě stejné řetězce):
(AB)*(AA(BA)*(A|BB)(AB)*)*
(A(AB)*(B|AA))*
Úkol 3 [1b]
Nalezněte nejmenší násobek devíti, jehož desítkový zápis vyhovuje tomuto výrazu:
(102)*101(201)*((0|202)(102)*101(201)*)*
Nezapomeňte, že součástí každého úkolu je přesvědčit opravujícího, že vaše
řešení je správně. Regex bez jakéhokoli vysvětlení není úplné řešení a nemá
nárok na plný počet bodů. Stejně tak konstatování „NE“, „10202010102“ nebo „nelze“…
Tím jsme uzavřeli kapitolu konečných automatů. Příště se vrátíme zpátky
k regexům, ukážeme si, jak se programem sed nahrazují řetězce za jiné,
co dělat, když regex pro náš požadovaný řetězec prostě neexistuje a jak s tím
vším souvisí Chuck Norris.
Řešení

 Pro zjednodušení si severní Ameriku i Evropu představme jako dva
konvexní
Pro zjednodušení si severní Ameriku i Evropu představme jako dva
konvexní 

 Příklad vstupu: Na prvním řádku jeho počáteční souřadnice a
Příklad vstupu: Na prvním řádku jeho počáteční souřadnice a  Každé písmeno se skládá z bodů a linií, které je spojují. V jednom bodě
může začínat i končit více linií. Při psaní perem lze psát víc navazujících
linií jedním tahem, nejde-li to, musí se pero zvednout a začít jinde. Kolikrát
nejméně je potřeba pero zvednout?
Každé písmeno se skládá z bodů a linií, které je spojují. V jednom bodě
může začínat i končit více linií. Při psaní perem lze psát víc navazujících
linií jedním tahem, nejde-li to, musí se pero zvednout a začít jinde. Kolikrát
nejméně je potřeba pero zvednout? Příklad vstupu:
Příklad vstupu: Jiný příklad:
Jiný příklad:
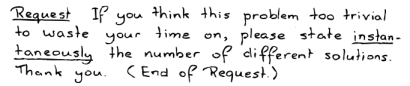
 Chudák pan Richards má jen svou zapomětlivou hlavu a pár papírů, tak budete
muset vymyslet, jak setřídit EWD v konstantní paměti. To jest, že si může
udělat třeba 1000 záznamů, ale ne pro každou z
Chudák pan Richards má jen svou zapomětlivou hlavu a pár papírů, tak budete
muset vymyslet, jak setřídit EWD v konstantní paměti. To jest, že si může
udělat třeba 1000 záznamů, ale ne pro každou z 

 Příklad vstupu:
Příklad vstupu: Tento text navazuje na předchozí dvě série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.
Tento text navazuje na předchozí dvě série, některé pasáže nemusí být
lehce pochopitelné bez jejich znalosti.