Třetí série dvacátého třetího ročníku KSP
Celý leták v PDF.
Řešení úloh
- 23-3-1: Úsporný kořen
- 23-3-2: Nejkratší cesta přes oceán
- 23-3-3: Skok bez padáku
- 23-3-4: Psaní písmen
- 23-3-5: Rozházené EWD
- 23-3-6: Výzkum veřejného mínění
- 23-3-7: Automaty stokrát jinak
23-3-1 Úsporný kořen (Zadání)
Řešitelé, kteří mají dobrou grafovou intuici nebo dostatečně naposloucháno, si uvědomili, že jde dokázat, že kýžené vrcholy najdou uprostřed nejdelší cesty stromu. Jan Bok si dobře všimnul, že v dávné úloze 18-1-3 Keřík už jsme dokonce obecnější variantu problému nejdelší cesty ve stromu řešili.
Vezmeme zavděk algoritmem, který takové pozorování nevyužívá. Bude se zakládat na opakovaném obírání stromu o listy. Nejdřív ale několik otázek:
Může být list stromu na alespoň třech vrcholech úsporný kořen? Nemůže, protože soused takového listu je ke všem ostatním vrcholům o jednotku bližší (každá cesta z listu k dalšímu vrcholu totiž vedla přes něj), takže bude mít o jednotku menší hlobuku.
Změní se množina úsporných kořenů odstraněním všech listů stromu na alespoň třech vrcholech? Ne, protože takovou operací zmenšíme hloubku všech zbylých vrcholů právě o jedničku – vrcholy s minimální hloubkou zůstanou tytéž.
Proč právě o jedničku? Hloubka každého vrcholu je dána vrcholy, které jsou od něj nejdál. To ale musí být listy, jinak by šlo onu vzdálenost měřící cestu protáhnout a hloubku zvětšit.
Tím, že odstraníme všechny listy, tedy odstraníme všechny důvody, proč by nemohla být hloubka o jednotku menší. O víc to být nemůže, protože sousedi odstraněných nejvzdálenějších listů svědčí o existenci cesty o jednotku kratší.
Je dobré si rozmyslet, kde argumentace selhává na stromech, které ani tři vrcholy nemají.
Teď už je zřejmá správnost algoritmu, který vrací výsledek sama sebe pro strom obraný o všechny své listy, je-li spouštěn na stromu s třemi a více vrcholy. Pro strom na jednom či dvou vrcholech je množina úsporných kořenů rovna množině vrcholů.
Algoritmus skončí, protože každý strom na alespoň dvou vrcholech obsahuje alespoň dva listy (jsou to třeba konce nejdelší cesty).
Abychom se vešli do lineární časové složitosti, předpočítáme si stupeň (počet sousedů) každého vrcholu a při každém odtrhávání listů si jej zaktualizujeme. Budeme si také udržovat seznam listů grafu – vrcholy z něj zanikají odtrháváním a přibývají snížením stupně na jednotku.
Odůvodněním lineárnosti pak budiž to, že odstranění každého vrcholu nám trvá konstantně času – nezapomeňme, že odstraňujeme listy, takže aktualizace seznamu sousedů a stejně tak stupně se týká jen jediného souseda tohoto odstraňovaného.
23-3-2 Nejkratší cesta přes oceán (Zadání)
Nejprve se podíváme na to, jak vypadá ona nejkratší úsečka, kterou hledáme. Její krajní body leží na obvodech zadaných mnohoúhelníků, takže buďto na nějaké straně, nebo v nějakém vrcholu mnohoúhelníka.
Navíc, když si po chvíli uvědomíme, že řešením určitě bude kombinace vrchol-strana, nebo vrchol-vrchol, tak už není žádný problém vyzkoušet všechny takové kombinace v čase O(N2). Může existovat i řešení strana-strana, ale pak existuje i jiné stejně dobré…
S trochou štěstí, třídění a binárního vyhledávání se dá takový algoritmus zrychlit až na O(N log N), ale to stále není žádná sláva.
Naservírujeme si tedy trochu geometrických důkazů a vykoukáme z nich algoritmus ještě výrazně rychlejší.
| XY |
| AB |
| AB |
| XY |
| AB' |
| AY |
| AX |
| AY |
| AX |
| AB |
Podobnou úvahou zjistíme, že pokud je řešením kombinace vrchol-vrchol, pak hledaná úsečka musí s oběma přilehlými stranami svírat alespoň pravý úhel, jinak na ni můžeme aplikovat argument z předchozích odstavců.
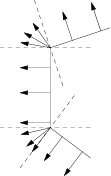
Takže pro každou hranu máme jen jeden směr, ve kterém z ní může vést hledaná úsečka, a pro každý vrchol interval směrů.
Co víc, mnohoúhelníky jsou konvexní, takže když si řekneme libovolný směr (úhel), tak nalezneme jen jedno místo na každém mnohoúhelníku, pro které tento směr připadá v úvahu.
Navíc jsme dostali ony mnohoúhelníky zadané jako body v pořadí na obvodu, takže můžeme jednoduše v lineárním čase postupně projít všechny možné směry.
Lze si to také představit tak, že máme dvě rovnoběžky, které otáčíme každou okolo jednoho z mnohoúhelníků stejným směrem (tak, abychom nepřeskočili žádný vrchol), a vždycky si ukládáme, kterého vrcholu se zrovna která ze přímek dotýká. Tak je také implementován vzorový program.
Jak zjistíme, že právě procházíme okolo řešení? Pokud je správným řešením kombinace vrchol-strana (A-BC), rozhodně se v jednu chvíli stane, že na jednom mnohoúhelníku máme zrovna vybraný bod A a na druhém přecházíme z B do C.
Navíc pro správné řešení jako jediné platí, že ABC je ostroúhlý trojúhelník, který se nepřekrývá se zadanými mnohoúhelníky. Důkaz je jednoduchý – od správného řešení se rozchází odpovídající si vrcholy na různé strany, viz obrázek.
Pro případ, že řešení je vrchol-vrchol, si ještě ukládáme vzdálenosti mezi projitými dvojicemi vrcholů. Pokud tedy doběhne cyklus bez toho, abychom vypsali výsledek a skončili, je správným řešením nalezené minimum vrchol-vrchol.
Čas je tedy O(N), paměť taktéž. Vyřešili jsme tedy úlohu tak rychle, jak rychle umíme načíst vstup.
 Existuje drsnější řešení, které využívá modifikaci půlení intervalu.
Jeho kompletní popis by vystačil na samostatný článek a jeho časová složitost
je O((log A)(log E)), kde A a E jsou počty vrcholů mnohoúhelníků. Nám
však bohatě stačilo řešení lineární.
Existuje drsnější řešení, které využívá modifikaci půlení intervalu.
Jeho kompletní popis by vystačil na samostatný článek a jeho časová složitost
je O((log A)(log E)), kde A a E jsou počty vrcholů mnohoúhelníků. Nám
však bohatě stačilo řešení lineární.
 V úloze se masivně používá analytická geometrie a vektorový počet. Za
zmínku stojí několik použitých faktů:
V úloze se masivně používá analytická geometrie a vektorový počet. Za
zmínku stojí několik použitých faktů:
- Bod se dá považovat za vektor.
- Skalární součin dvou vektorů a, b je roven |a||b|cosφ, tedy je kladný, pokud svírají ostrý úhel, záporný pro tupý úhel a nula pro pravý úhel φ.
- Normálový vektor aN je kolmý na vektor a
- Skalární součin vektoru a a normálového vektoru bN je kladný, je-li vektor b „na jedné straně“ od vektoru a, jinak záporný (a pro vektory opačného směru nulový). Kladná a záporná strana závisí na definici normálového vektoru (je-li to „ten kolmý vlevo“, nebo „ten kolmý vpravo“).
23-3-3 Skok bez padáku (Zadání)
Úloha má přehršel parametrů a u takových se obvykle stává, že složitost různých řešení závisí na různých parametrech. Tak si je pojďme pojmenovat:
| (x0,y0) | počáteční pozice |
| h0 | výška, ze které smíme spadnout |
| T | počet trampolín |
| W | šířka (pozice nejpravější trampolíny) |
Ujasnění zadání. Zadání zarytě mlčí o dvou důležitých věcech:
- Jsou souřadnice celočíselné? Nikoho z řešitelů naštěstí nenapadlo, že by nemusely být, tak to předpokládejme také. (Jinak by totiž úloha byla mnohem zákeřnější – byla by vůbec řešitelná v konečném čase?)
- Co se stane, když padáme z výšky 1? Pak by měl následovat odraz do výšky 0. A pokud spadneme na jednu z několika sousedních trampolín, můžeme po nich pak volně chodit a na kraji seskočit dolů? Raději nulové odrazy zakážeme. (Kdybychom je opravdu chtěli, náš algoritmus půjde snadno upravit, aby s nimi počítal.)
Pár pozorování pro začátek. Předně, pokud spadneme z bodu (x,y) na trampolínu (x,t), odrazíme se do výšky y' = ⌊(y+t)/2 ⌋ a odtamtud se posuneme buďto do (x-1,y'), nebo do (x+1,y'). Jelikož t<y (trampolína leží pod námi) a nulové odrazy jsme zakázali, musí být i y'<y. Takže postupně padáme z čím dál tím nižších bodů.
Proto ať už se odrážíme jakkoliv, po konečně mnoha odrazech spadneme na zem (živí či mrtví; se schrödingerovsky kočkovitými parašutisty nepočítáme). Dokonce víme, že odrazů je vždy nejvýše y0.
Rekurzivní řešení. Nejprve se podíváme na první podúlohu. Chceme tedy naprogramovat funkci, která dostane počáteční polohu (x0,y0) a oznámí, jaký je minimální počet odrazů, chceme-li přežít (nebo +∞, pokud nemáme šanci). Tato funkce si může spočítat, která trampolína leží pod zadaným bodem, odrazit se od ní, a vyzkoušet jak posunutí doleva, tak doprava.
Každá z těchto možností zase dává nějaký bod, ze kterého budeme padat. Který si vybrat? Nevíme. Tak zkusíme oba. Pro každý se zavoláme rekurzivně a zjistíme, která možnost dává menší počet odrazů. O 1 větší počet pak prohlásíme za svůj výsledek. Jak už víme, stále klesáme, takže výpočet se nemůže zacyklit.
Zbývá ošetřit triviální případ, totiž ten, že už pod námi žádná trampolína neleží. Pak podle toho, zda už jsme v bezpečné výšce, vrátíme buď 0, nebo +∞.
Toto je jistě funkční řešení, bohužel ale poněkud hlemýždí – pro každý odraz se dvakrát rekurzivně voláme, takže pro nejvýše y0 odrazů dostáváme exponenciální časovou složitost O(2y0). (Náš odhad počtu odrazů je poněkud přemrštěný, ale i s tím správným, který časem dokážeme, vyjde exponenciála.)
Jak neopakovat výpočty. Čím všechen ten čas trávíme? Inu, počítáme pořád dokola totéž. Vstupem naší funkce je totiž dvojice souřadnic a různých dvojic existuje pouze W×y0.
Algoritmus tedy můžeme vylepšit tím, že si pořídíme pole („blbenku“) a budeme si v něm pamatovat, pro které počáteční polohy už známe výsledek a jaký je. Před každým voláním funkce se tam podíváme a pokud už hodnotu známe, použijeme ji. Jinak volání provedeme a výsledek si poznamenáme. Tím celkový počet volání snížíme na O(Wy0).
Jak najít trampolínu. V předchozím rozboru jsme poněkud zamluvili, že potřebuje pro zadanou polohu zjistit, jaká je nejbližší nižší trampolína. Na to by se dalo jít všelijak chytře, třeba si souřadnice trampolín setřídit lexikograficky a pak v nich půlením intervalu hledat.
My na to ale půjdeme jinak: předpočítáme si „navigační tabulku“ tvaru W×y0, která nám pro každý bod řekne, jak hluboko pod ním je trampolína.
Nejprve tabulku vyplníme nulami, jen na pozice trampolín napíšeme jedničky. Pak pole projdeme zespoda nahoru a doplňujeme hodnoty. Jedničky zůstanou jedničkami, pro každou nulu se podíváme, co je pod ní. Pokud nula, ponecháme naši nulu. Pokud něco jiného, naše hodnota bude o 1 větší. Výpočet tabulky tedy bude trvat čas O(Wy0+T).
Každý krok našeho rekurzivního algoritmu s blbenkou teď už umíme provést v konstantním čase, celý algoritmus tedy poběží v čase O(Wy0+T).
Zespoda nahoru. Rekurzi s blbenkou obvykle můžeme zjednodušit na dynamické programování. Tím myslíme, že budeme blbenku rovnou počítat zespoda nahoru – pro výpočet každé hodnoty potřebujeme jenom hodnoty z nižších řádků, které už budeme mít spočítané.
Přesněji řečeno, označíme si P[x,y] minimální počet odrazů při pádu z bodu (x,y) a budeme zespoda nahoru provádět toto:
- Pokud pod (x,y) neleží žádná trampolína, položíme
![P[x,y] = 0 pro y ≤ h0, P[x,y] = +∞pro y > h0.](s2333-eq.png)
- Leží-li pod (x,y) trampolína (x,t), spočítáme výšku po odrazu y'=⌊y+t⌋
a položíme Ptáme-li se na hodnotu mimo tabulku, použijeme +∞.
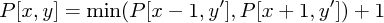
S předvýpočtem navigační tabulky seběhne tento algoritmus opět v čase O(Wy0+T), ale je daleko jednodušší. Proto jsme ukázkový program psali podle něj.
Podúloha b. Druhou podúlohu, totiž stanovení všech výšek, ze kterých spadnuvše bychom přežili, získáme jako vedlejší produkt právě popsaného algoritmu. Stačí se totiž do tabulky P podívat na x0-tý sloupec a vypsat ta y, pro něž je P[x0,y] konečné. To stihneme v čase O(y0), takže nám to časovou složitost nezhorší.
 Pseudopolynomiální složitost.
Algoritmus, který jsme si ukázali, má takzvaně pseudopolynomiální složitost.
Tím se myslí, že složitost není polynom ve velikosti vstupu, nýbrž v hodnotách
čísel obsažených na vstupu. U opravdového polynomiálního algoritmu by tedy
směla záviset pouze na T, nikoliv na y0, h0 nebo W. Případně pokud
bychom (jak se často činí) měřili velikost vstupu v bitech, byla by vzhledem
k velikosti vstupu polynomiální také čísla log y0, log h0 a log W.
Neuměli bychom najít poctivé polynomiální řešení?
Pseudopolynomiální složitost.
Algoritmus, který jsme si ukázali, má takzvaně pseudopolynomiální složitost.
Tím se myslí, že složitost není polynom ve velikosti vstupu, nýbrž v hodnotách
čísel obsažených na vstupu. U opravdového polynomiálního algoritmu by tedy
směla záviset pouze na T, nikoliv na y0, h0 nebo W. Případně pokud
bychom (jak se často činí) měřili velikost vstupu v bitech, byla by vzhledem
k velikosti vstupu polynomiální také čísla log y0, log h0 a log W.
Neuměli bychom najít poctivé polynomiální řešení?
 Lepší odhad na počet odrazů.
Především si všimneme, že naše omezení počtu odrazů číslem y0 bylo naprosto
přemrštěné. Zaměřme se na jednu trampolínu a sledujme výšky, do kterých se
dostaneme po jednotlivých odrazech. Kdyby žádné jiné trampolíny neexistovaly
(a dovolili bychom si na chvíli po odrazu neuhnout doleva ani doprava), dělila
by se po každém odrazu výška dvěma, takže po řádově log y0 odrazech by
byla nulová. Teď vrátíme ostatní trampolíny do hry a všimneme si, že tím,
že jsme si na ně odskočili (doslova), jsme si při dalším návratu na naši
trampolínu mohli výšku jedině zmenšit. Takže i tehdy je počet odrazů
o jednu trampolínu nejvýše log y0 a celkem se proto můžeme odrazit
nejvýše (T log y0)-krát.
Lepší odhad na počet odrazů.
Především si všimneme, že naše omezení počtu odrazů číslem y0 bylo naprosto
přemrštěné. Zaměřme se na jednu trampolínu a sledujme výšky, do kterých se
dostaneme po jednotlivých odrazech. Kdyby žádné jiné trampolíny neexistovaly
(a dovolili bychom si na chvíli po odrazu neuhnout doleva ani doprava), dělila
by se po každém odrazu výška dvěma, takže po řádově log y0 odrazech by
byla nulová. Teď vrátíme ostatní trampolíny do hry a všimneme si, že tím,
že jsme si na ně odskočili (doslova), jsme si při dalším návratu na naši
trampolínu mohli výšku jedině zmenšit. Takže i tehdy je počet odrazů
o jednu trampolínu nejvýše log y0 a celkem se proto můžeme odrazit
nejvýše (T log y0)-krát.
 Odstranění závislosti na W.
Závislosti na parametru W (šířce mapy) se můžeme zbavit snadno.
Všimneme si totiž, že se ve vodorovném směru nikdy nedostaneme dál
než o T kroků od počátku. Do vzdálenosti T+1 musí přeci ležet
aspoň jeden sloupec bez trampolíny a ten nemáme jak přeskočit.
Stačí tedy pole P v našem algoritmu omezit na velikost (2T+1)×y0
(sloupec odpovídající souřadnici x0 bude uprostřed) a trampolíny
ležící mimo ignorovat. Tím časovou složitost zlepšíme na O(Ty0).
Odstranění závislosti na W.
Závislosti na parametru W (šířce mapy) se můžeme zbavit snadno.
Všimneme si totiž, že se ve vodorovném směru nikdy nedostaneme dál
než o T kroků od počátku. Do vzdálenosti T+1 musí přeci ležet
aspoň jeden sloupec bez trampolíny a ten nemáme jak přeskočit.
Stačí tedy pole P v našem algoritmu omezit na velikost (2T+1)×y0
(sloupec odpovídající souřadnici x0 bude uprostřed) a trampolíny
ležící mimo ignorovat. Tím časovou složitost zlepšíme na O(Ty0).
 Závislost na y0.
Ve svislém směru to nedopadne tak skvěle. Nabízí se využít
toho, že během jednoho seskoku spadneme na jednu trampolínu nejvýše
(log y0)-krát, takže bychom políčka nad touto trampolínou mohli
rozdělit na nějaké intervaly, uvnitř kterých je P[x,y] konstantní,
a pamatovat si pouze hranice intervalů a jednu hodnotu pro každý z nich.
Takových algoritmů se dá vymyslet vícero, ale všechny selžou na tom,
že v různých seskocích může být toto rozdělení na intervaly různé,
takže intervaly se mohou množit a množit, až jich nakonec bude řádově y0.
Závislost na y0.
Ve svislém směru to nedopadne tak skvěle. Nabízí se využít
toho, že během jednoho seskoku spadneme na jednu trampolínu nejvýše
(log y0)-krát, takže bychom políčka nad touto trampolínou mohli
rozdělit na nějaké intervaly, uvnitř kterých je P[x,y] konstantní,
a pamatovat si pouze hranice intervalů a jednu hodnotu pro každý z nich.
Takových algoritmů se dá vymyslet vícero, ale všechny selžou na tom,
že v různých seskocích může být toto rozdělení na intervaly různé,
takže intervaly se mohou množit a množit, až jich nakonec bude řádově y0.

 Je tato hrozba reálná? Bohužel ano – ukážeme konstrukci vstupu, který se
v těchto ohledech chová značně ošklivě. Předem varujeme, že to nebude úplně
snadné; čtenář neprahnoucí po dobrodružství nechť raději přeskočí k podpisu
autora na konci řešení.
Je tato hrozba reálná? Bohužel ano – ukážeme konstrukci vstupu, který se
v těchto ohledech chová značně ošklivě. Předem varujeme, že to nebude úplně
snadné; čtenář neprahnoucí po dobrodružství nechť raději přeskočí k podpisu
autora na konci řešení.
Ještě tu jste? Dobrá, jdeme na to. Nejdříve si uvědomíme, jak se mění souřadnice, když se během jednoho seskoku odrážíme postupně od trampolín ve výškách t1, t2, … , tn. Už víme, že po prvním odrazu vyskočíme do výšky y1 = (y0 + t1)/2 (zaokrouhlení s dovolením zanedbáme a pak budeme volit výšky tak, aby vždy vyšlo celé číslo). Obecně yi = (yi-1 + ti)/2. Pokud tyto vztahy složíme dohromady, dostaneme:
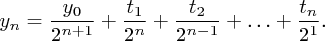
Naše konstrukce bude vypadat tak, že si zvolíme nějaká čísla x1,… ,xT a rozmístíme T trampolín na souřadnice (n-i,xi). Uvažujme, do jakých výšek nad nejpravější trampolínou se můžeme dostat při různých způsobech seskoku. Ukážeme, že možných výšek je spousta, a to dokonce i tehdy, když se omezíme na některé speciální druhy seskoků.
Kterýkoliv seskok můžeme jednoznačně popsat posloupností rozhodnutí o směru
doleva/doprava po jednotlivých odrazech. Nás budou zajímat pouze seskoky
složené z úseků tvaru PPLP nebo PLPP. Všimněte si, že každý takový úsek nás
posune přesně o 2 trampolíny doprava, takže po T/2 úsecích proskáčeme celou
posloupnost trampolín; celkem se při tom odrazíme 2T-krát.
Nyní použijeme vzoreček (*) a uvážíme, jak k finální výšce přispějí trampolíny v i-tém úseku. Úseky přitom očíslujeme od nultého úplně vpravo, takže i-tý úsek bude složený z trampolín (n-2i-2,x2i+2) a (n-2i-1,x2i+1) a navštívíme ho ve skocích s vahami (to jsou ty mocniny dvojky ve vzorečku) 24i+4 až 24i+1.
Pokud ho proskáčeme způsobem PPLP, přispěje k součtu hodnotou
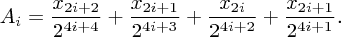
PLPP:
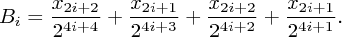
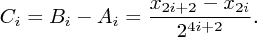
PLPP.
Uvažujme nyní nějakou obecnou posloupnost přirozených čísel z0,… ,zK (K=T/2-2). V naší konstrukci nastavíme xi=0 pro všechna lichá i, dále položíme x0=0 a x2j+2 = x2j + zj·24j+2 pro všechna j. Navíc zvolíme počáteční výšku y0 tak, aby byla větší než 22T+1·maxi xi – tím zařídíme, že se během seskoku délky 2T nemůžeme dostat pod žádnou z navržených trampolín.
Touto volbou hodnot xi jsme zařídili, že rozdíly Ci z předchozího výpočtu jsou rovny právě zi. Jinými slovy, výšky dosažitelné zkoumanými druhy seskoků se dají napsat konstanta plus součet nějaké podmnožiny čísel zi.
K dokončení stačí klasický trik: z mocnin dvojky 20,… ,2K se dají nasčítat všechna čísla od 0 do 2K+1-1 (tak funguje dvojková soustava). Pro volbu zi=2i tedy existuje alespoň 2K+1 dosažitelných výšek, což je exponenciálně mnoho vzhledem k T.
Navíc počty použitých trampolín odpovídají počtu jedniček v binárním zápisu čísla, což se mění příliš rychle na to, aby intervalů mohlo být řádově méně. EPA (Est post aves. To je něco jako „Quod erat demonstrandum.“, ale znamená to „A je po ptákách.“).
23-3-4 Psaní písmen (Zadání)
Poznámka redakce: Zadavatel této úlohy do CodExu ji pozměnil. Oproti zadání v letáku a na webu byl na vstupu zadán graf explicitně rozsekaný na komponenty. Navíc zadání v CodExu vyžadovalo optimalizaci na paměť. Tomu odpovídá i zdrojový kód.
Abychom mohli úlohu vyřešit, měli bychom vědět, co jsou to eulerovské tahy a jaké podmínky splňují grafy, které je obsahují (nahlédnout můžete do našich grafových kuchařek). To, že jde obrázek nakreslit jedním tahem, znamená, že obsahuje uzavřený či otevřený eulerovský tah.
Pokud souvislý graf obsahuje pouze vrcholy sudého stupně, je v něm možno nalézt uzavřený eulerovský tah.
Co se stane, pokud neobsahuje pouze vrcholy sudého stupně? Mezi dvojici lichých vrcholů přidáme hranu (opakujeme, dokud máme vrcholy lichého stupně), takto postupně dostaneme graf, ve kterém jsou všechny vrcholy sudého stupně, tedy obsahuje uzavřený eulerovský tah.
Nyní odebereme hrany, které jsme přidali, a tento eulerovský tah se nám rozpadne na několik hranově disjunktních tahů, které vždy začínají a končí v nějakém vrcholu lichého stupně (jeden počáteční lichý vrchol a jeden koncový lichý vrchol pro každý tah), tudíž celkový počet těchto tahů je počet lichých vrcholů děleno dvěma.
Žádný vrchol lichého stupně nemůže být uprostřed tahu, tudíž tahů nemůže být méně, než jsme našli.
Stačí nám vědět, kolik takových tahů potřebujeme, není tedy potřeba je konstruovat, stačí nám určit počet lichých vrcholů (a dát si pozor na grafy bez lichých vrcholů).
Samotné řešení úlohy (provedeme pro každou komponentu souvislosti samostatně):
Potřebujeme pole délky n (počet vrcholů), při načítání si v něm udržujeme stupně jednotlivých vrcholů. Po načtení projdeme toto pole a určíme počet lichých vrcholů, který vydělíme 2. Dostaneme, kolikrát musíme zvednout pero při kreslení grafu.
Paměťová složitost: O(n).
Časová složitost: O(m+n), kde m je počet hran grafu.
23-3-5 Rozházené EWD (Zadání)
Úkolem bylo setřídit zadaný jednosměrný spojový seznam co nejrychleji, ale v konstantní paměti, což znamená jen s předem daným počtem proměnných, bez rekurze a dalších pomocných polí, tedy pouze přepojováním původního spojového seznamu.
Určitě bylo dobrým nápadem podívat se do naší (tradiční české) kuchařky o třídění. A co s tak malou pamětí? Bublinkové třídění (bubble sort) bude zcela jistě fungovat, protože v průběhu algoritmu prohazujeme jen dva sousední prvky, což lze udělat jednoduše.
Bublinkové třídění má navíc pěknou vlastnost, že třídění již setříděných dat trvá pouze O(N). Jenže nejhůře a dokonce i průměrně vyjde asymptotická složitost O(N2). Je to nejrychlejší možný výsledek za daných podmínek, nebo ne?
Než si řekneme řešení, uveďme si dolní odhad složitosti. Jelikož stáří záznamů EWD můžeme akorát tak porovnávat (nic o nich nevíme), platí důkaz uvedený na konci kuchařky o třídění, a tedy určitě nevymyslíme algoritmus s průměrnou složitostí lepší než O(N log N).
Takový algoritmus skutečně existuje. My si ukážeme, jak modifikovat třídění sléváním (Mergesort) se zachováním složitosti v nejhorším případě i v průměru O(N log N), na což přišlo i několik řešitelů. Nevylučuji však, že nepůjde upravit jiný algoritmus, i když třídění haldou ani Quicksort nejspíš převést na řešení úlohy nelze.
Jak funguje takový běžný Mergesort na třídění pole? Ten si nejprve rozdělí pole na dvě půlky, ty setřídí stejným algoritmem (zavolá se na každou rekurzivně) a pak je „slije“: odebírá vždy menší z prvků na začátku obou setříděných půlek pole a vkládá je do nového pole. Podrobnější popis opět v kuchařce.
Nyní upravíme Mergesort pro potřeby naší úlohy. Jelikož nesmíme použít rekurzi, nebudeme postupovat „odshora dolů“ (postupně půlíme data na co nejmenší části), ale „odspoda nahoru“ (spoustu malých setříděných částí sléváme postupně do jedné).
V prvním kroku se podíváme na všechny dvojice sousedních prvků (každý prvek je nejvýše v jedné dvojici), porovnáme prvky dvojice a případně je prohodíme, což v případě spojového seznamu znamená přepojení odkazů. V druhém kroku sléváme vždy dvě sousední dvojice prvků do setříděné čtveřice, v třetím dvě čtveřice do osmice…
Obecně v k-tém kroku slijeme dvě sousední části o 2k prvcích. Až slijeme všechny prvky do jedné setříděné posloupnosti, máme vyhráno.
Často se může stát, že poslední slévaný úsek v k-tém kroku nemusí mít 2k prvků, ale to vůbec nevadí (jeden slévaný úsek bude menší). Podobně lichý počet slévaných úseků (nemůžeme je spárovat do dvojic) ošetříme prostým ignorováním posledního úseku. V nějakém pozdějším kroku musí být tento úsek slit se zbytkem, třeba pro 2n + 1 prvků se bude poslední prvek slévat až v posledním kroku.
Nyní pojďme na implementaci slévání dvou setříděných úseků ve spojovém seznamu
(ne nutně stejné délky) s konstantní pomocnou pamětí. Budeme si pamatovat odkaz
na prvek před prvním úsekem (tedy poslední prvek již slité části) v proměnné
prvek1 a odkaz na prvek před druhým úsekem v proměnné prvek2.
Na začátku slévání dvou úseků nejprve posuneme odkaz prvek2 o délku
prvního úseku za odkaz prvek1. Abychom mohli kontrolovat, jestli
v nějakém úseku nedošly prvky, vytvoříme si dvě proměnné delka1 a
delka2, v nichž budou počty zbývajících prvků v úsecích.
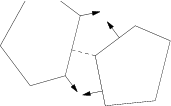
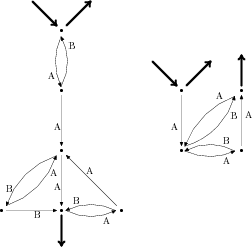
Pak postupně bereme prvky ze začátku obou úseků (následníky prvku prvek1
a prvek2) a menší z nich přepojíme za prvek prvek1. Je-li to prvek
z prvního seznamu, stačí posunout odkaz prvek1 o jeden prvek dopředu,
jinak je to následník prvek2 (označme ho p), který přepojíme za
prvek1 takto: následníkem p bude následník prvek1,
následníkem prvek1 bude p, následníkem prvek2 bude původní
následník p.
Jestli vás předchozí odstavec zmátl, vůbec se nedivím a raději předkládám
obrázek (tečkované šipky ukazují přepojení prvku p):
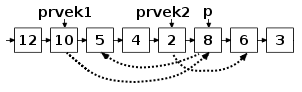
Je vidět, že potřebujeme jen konstantně mnoho pomocné paměti. Co se týče časové složitosti, bude pro jakákoliv data O(n log n), kde n je počet prvků. V k-tém kroku totiž sléváme úseky o 2k prvcích, a bude-li 2k > n/2, získáme po tomto kroku celý setříděný spojový seznam. Odtud zlogaritmováním dostaneme, že stačí log2 n kroků, přičemž v každém provedeme O(n) operací.
Program včetně čtení vstupu (C)
23-3-6 Výzkum veřejného mínění (Zadání)
Tato úloha měla spoustu možností, jak ji řešit. My si ukážeme jedno kvadratické řešení a pak řešení v čase O(N log N). Nejdříve se podíváme na kvadratické řešení.
Vstupní posloupnost si načteme do dvou polí. V poli X budeme mít posloupnost, tak jak přišla na vstupu, a do pole Y uložíme posloupnost setříděnou podle velikosti.
Nyní si všimneme, že každá dvě po sobě jdoucí čísla v poli X nám určují intervaly mezi vstupními období (kde popularita klesá/stoupá) a dvě po sobě jdoucí čísla v poli Y určují intervaly hodnot, které budou mít stejnou četnost výskytů.
My tedy z každého intervalu v poli Y vezmeme libovolnou hodnotu, (například prostřední), a spočítáme, kolikrát se vyskytuje v intervalech pole X.
Nyní k řešení pracující v čase O(N log N). Existuje spousta způsobů, jak na úlohu jít. My si ukážeme techniku zvanou Zametání přímkou (line sweep), pomocí které se mimo jiné dají řešit i některé geometrické úlohy.
Představme si, že se ke grafu popularity blíží přímka rovnoběžná s osou x. Tato přímka začne v minus nekonečnu, projde grafem od zdola nahoru a skončí v plus nekonečnu. Nás v každém okamžiku bude zajímat, kolikrát přímka protíná graf.
Všechny okamžiky ale testovat nemůžeme, tak se budeme věnovat jen těm, ve kterých se počet průsečíků s přímkou mění. Takovým okamžikům budeme říkat události a tyto události budeme zpracovávat v pořadí, v jakém nastanou při průchodu od zdola nahoru.
V našem případě jsou události všechny body, ve kterých se mění počet průsečíků s přímkou. Všimneme si, že tento počet se nám bude měnit pouze v lokálních maximech a minimech (tam, kde je špička). V maximu nastanou dvě události: nejdříve se počet průsečíků zmenší o jedna (došli jsme do špičky) a poté špičku opustíme a počet průsečíků se znova zmenší o jedna. Podobné budou i události u minima.
My si tedy pro každý bod vytvoříme příslušné události (pozor, u krajních bodů je pouze událost opuštění/přidání špičky) a tyto události si setřídíme primárně podle výšky a sekundárně podle jejich priority.
Priorita událostí je:
- změna na špičku maxima
- přidání špičky minima
- opuštění špičky maxima
- rozdvojení špičky u minima
Zkuste si rozmyslet, proč jsou priority událostí právě takto a v jakém případě může nastat problém, kdyby žádné priority nebyly.
Teď už jen postupně zpracováváme všechny události a po každém zpracování zkontrolujeme, jestli nejsme v maximálním počtu průsečíků. Po zpracování všech událostí vypíšeme výsledek.
Na první pohled to vypadá docela složitě, ale vlastně je to jednoduché. Viz zdrojový kód.
23-3-7 Automaty stokrát jinak (Zadání)
Třetí sérií uzavíráme seriálovou odbočku k automatům. Ještě nám chybí vysvětlit převod NKA na DKA a redukci automatu.
Nejprve si ukážeme převod NKA na DKA třeba na zadání úkolu 1. Označíme si jednotlivé stavy třeba písmeny A až I jako na obrázku (ten stav uprostřed je E, jen se to tam nevešlo).
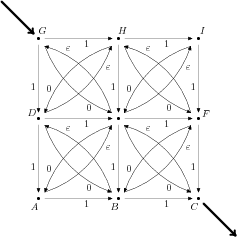
Nyní budeme konstruovat DKA, ve kterém budou jako stavy množiny stavů původního NKA. Vstupní stav je G. Z něj se můžeme dostat přečtením 1 do {D,H} a přečtením 0 do {G,E,I}.
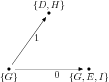
Kam se nyní můžeme dostat z {D,H} přečtením 0? Ze stavu D jde jít do B (a pak po ε hranách do D, F a H), z H jde jít do D a F (a po ε hranách do H), tedy z {D,H} vede hrana popsaná 0 do stavu {B,D,F,H}.
Analogicky z {D,H} přečtením 1 dojdeme do {A,E,G,I}. Z {G,E,I} pak vedou hrany 0 a 1 do {A,C,E,G,I} a {B,D,F,H}.
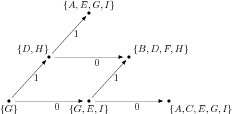
Stejným způsobem pak ještě doplníme hrany z nově vzniklých tří stavů (další už nevzniknou, ale teoreticky by mohly – výsledný DKA může mít až 2N stavů oproti NKA s N stavy).
Výstupní stavy jsou pak všechny ty, v jejichž množinách se vyskytuje alespoň jeden výstupní stav původního NKA. V tom byl v našem případě výstupním stavem jen C, který se i ve výsledném automatu vyskytuje v jediném stavu. Ten je tedy výstupním.

Na obrázku vidíte kompletní zkonstruovaný DKA a zároveň řešení úkolu 1.
Když jste převedli oba dva výrazy z úkolu 2 na NKA (postupem z minulé série) a touto metodou na DKA, dostali jste přibližně tyto dva automaty:
Věřili byste, že jsou ekvivalentní, tedy že přijímají stejný jazyk? Na první pohled to tak rozhodně nevypadá, ale jsou.
Jak na to přijdeme?
Ukážeme si postup zvaný „redukce automatu“, kdy nalezneme všechny stavy, které jsou ekvivalentní, a sloučíme je. Například si můžeme všimnout, že u řešení úkolu 1 by šlo sloučít (nerozlišitelné) stavy {A,E,G,I} a {G,E,I}. Ať přečtu cokoli, skončím na stejném místě.
| A | B | ||
| → 1 | 2 | – | ω |
| 2 | 3 | 1 | α |
| 3 | 5 | 4 | α |
| 4 | 3 | 5 | α |
| 5 | 6 | – | ω |
| 6 | 3 | 5 | α |
Zapíšeme si levý automat tabulkou. Se šipkou je vstupní stav, podtržen je výstupní. Ve sloupci vpravo jsou pak zapsány kategorie stavů – jak by automat z tohoto stavu pokračoval, kdyby na vstupu už nebyl žádný znak.
Tabulku budeme dále rozšiřovat. Předpokládejme, že je na vstupu o znak víc:
| A | B | A | B | |||
| → 1 | 2 | – | ω | α | – | ω |
| 2 | 3 | 1 | α | α | ω | α |
| 3 | 5 | 4 | α | ω | α | β |
| 4 | 3 | 5 | α | α | ω | α |
| 5 | 6 | – | ω | α | – | ω |
| 6 | 3 | 5 | α | α | ω | α |
Zjistili jsme, jak se automat chová po přečtení jednoho znaku. Vidíme, že stavy 2, 4 a 6 jsou nerozlišitelné, pokud přečteme maximálně jeden znak ze vstupu. Taktéž stavy 1 a 5.
Třetí, separátní kategorii jsme museli zavést pro stav 3, který se začal lišit od stavů 2, 4 a 6.
Provedeme ještě jeden krok a zjistíme, že se už kategorie stavů nezměnily.
| A | B | A | B | A | B | ||||
| → 1 | 2 | – | ω | α | – | ω | α | – | ω |
| 2 | 3 | 1 | α | α | ω | α | β | ω | α |
| 3 | 5 | 4 | α | ω | α | β | ω | α | β |
| 4 | 3 | 5 | α | α | ω | α | β | ω | α |
| 5 | 6 | – | ω | α | – | ω | α | – | ω |
| 6 | 3 | 5 | α | α | ω | α | β | ω | α |
Jedna hezká věta říká, že jakmile se jednou nezmění kategorie stavů, nezmění se nikdy. To je docela jasně vidět, když si uvědomíte, že by se vlastně pořád dokola opakovaly stejné trojice sloupečků.
| A | B | |
| → ω | α | – |
| α | β | ω |
| β | ω | α |
Další hezká věta říká, že poslední trojice sloupečků nám popisuje tzv. redukovaný automat, který je ekvivalentní s tím původním. Duplicitní řádky vynecháme.
Když pak provedeme totéž pro druhý automat, dostaneme podobnou tabulku.
| A | B | A | B | A | B | ||||
| → 1 | 2 | – | α | β | – | α | β | – | α |
| 2 | 3 | 4 | β | β | α | β | γ | α | β |
| 3 | 4 | 2 | β | α | β | γ | α | β | γ |
| 4 | 2 | – | α | β | – | α | β | – | α |
| A | B | |
| → α | β | – |
| β | γ | α |
| γ | α | β |
Automaty tedy jsou ekvivalentní, neboť jejich redukované verze jsou ekvivalentní (stačí tabulky přepísmenkovat). Proto i dva zadané regexy jsou ekvivalentní, tedy popisují stejný jazyk.
Jedno obtížně dokazatelné tvrzení říká, že pokud jsou dva automaty ekvivalentní, pak je lze zredukovat tímto postupem na stejný DKA, až na isomorfismus.
Isomorfní DKA jsou takové, že pokud správně přečíslujeme stavy jednoho z nich, tak dostaneme druhý automat. Ač se to nezdá, na problém neznáme polynomiální algoritmus, ale ani nevíme, jestli je NP-úplný.
A jaké bylo správné řešení úkolu 3? 10101010101201 je nejmenším
násobkem devíti vyhovujícím zadanému výrazu. Bylo potřeba si všimnout, že
všechny ohvězdičkované trojice jsou násobky 3, takže přinejhorším nějakou
vložíme na konec.
Na začátku byla povinně trojice 101 s ciferným součtem 2. V každé iteraci
velké závorky musela být zase trojice 101 a navíc buďto 0, nebo
202. První varianta měla ciferný součet 2, druhá 6.
Krátkým rozborem případů pak došlo na to, že nejkratší násobek 3 vyhovující
regexu je 10101010101. Přilepením 201 za něj pak vypadl kýžený
nejmenší násobek 9.
Většina řešitelů obdržela téměř plný počet bodů, nejčastější chybou bylo opomenutí popisu, které stavy budou vstupní a které výstupní po převodu DKA na NKA. Obecně však byla vaše řešení hezká a bylo mi potěšením je opravovat.