První série dvacátého pátého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

Řešení úloh

• 25-1-1: Fotografování
• 25-1-2: Stánky na náměstí
• 25-1-3: Řazení hradní stráže
• 25-1-4: Útěk
• 25-1-5: Algoritmus sekretářky
• 25-1-6: Sekání trávy
• 25-1-7: GPS log
• 25-1-8: Sázíme v TeXu

---

25-1-1 Fotografování (Zadání)

---

---

25-1-2 Stánky na náměstí (Zadání)

---

Pro zjištění, zdali mají dva stánky kolizi mezi sebou, použijeme tzv. sweep-line („zametací přímku“). Představíme si, že budeme mít pomyslnou přímku rovnoběžnou (např.) s osou X a budeme s ní posouvat z y=-∞ do y=+∞. Tímto nám postupně protne všechny stánky (viz následující obrázek).

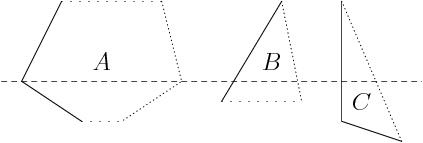
Na něm máme znázorněny stánky A, B a C a pomyslnou přímku zobrazenou čárkovaně. Plnou čárou jsou označeny levé okraje mnohoúhelníků (stánků), hustě tečkovanou pravé okraje a řídce tečkovanou okraje rovnoběžné s osou X.

Jak si můžeme všimnout, mnohoúhelníky nám rozdělují přímku na několik intervalů (dle jejich průsečíků). Bez kolize stánků se nám na sweep-line pravidelně střídají jejich levé a pravé okraje. Pokud bychom měli dva levé (či pravé) okraje vedle sebe, došlo by k překrytí vnitřků mnohoúhelníků.

Základem programu tedy bude udržovat si informace o tom, jak vypadá rozdělení na intervaly odpovídající jednotlivým mnohoúhelníkům. V této struktuře budeme potřebovat být schopni rychle provést následující:

• Přidat mnohoúhelník – ve chvíli, kdy se sweep-line dotkne jeho spodního okraje
• Odebrat mnohoúhelník – ve chvíli, kdy sweep-line opustí jeho nejvyšší bod
• Opravit intervaly ve chvíli, kdy narazíme na bod, kde se levý či pravý okraj láme (tj. kdy se dostaneme na některý vrchol mnohoúhelníku)

První operace vyžaduje, abychom byli schopni rychle vyhledat, které mnohoúhelníky budou vlevo a vpravo od vkládaného. Proto pro reprezentaci rozdělení sweep-line stánky budeme používat intervalový strom (v programu užit AVL strom kvůli vyvažování – viz kuchařku o vyhledávacích stromech). Tím dosáhneme vyhledání, kam máme nový stánek zatřídit, v čase O(log T).

V klasickém intervalovém stromu však ukládáme krajní body – ty se nám ale mění, jak se posouvá sweep-line, a přepočítavat je po každém kroku je pracné. Můžeme si však všimnout, že dokud nedojde ke zkřížení okrajů mnohoúhelníků (viz obrázek níže), nebude se měnit pořadí, v jakém intervaly budou na přímce za sebou. Odtud je už jen krůček k myšlence, že není nutné okraje intervalu reprezentovat pomocí dvou bodů, ale je možné užít i dvou úseček (okraje mnohoúhelníku) a vlastní bod bude průsečíkem úsečky a aktuální sweep-line.

Jak můžou kolize stánků (z hlediska přímky) vypadat? Jedna možnost je, že dojde ke zkřížení okrajů (A s B, či C s D).

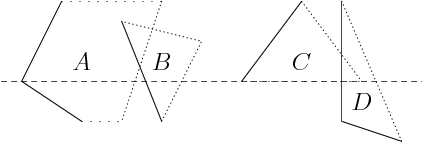
To nemusí být nalezeno jen při vkládání nového mnohoúhelníku, ale i po dosažení vrcholu některého stánku a změně „aktuální“ okrajové úsečky.

Další možnost je, že vkládaný mnohoúhelník je uvnitř jiného (B v A) či jiný stánek bude mezi okraji vkládaného (D v C).

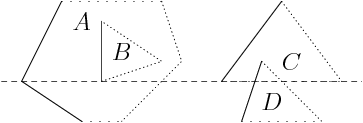
Tyto situace se však v intervalovém stromě snadno detekují – v čase O(log T) je možno zjisit, jaký okraj bude levým sousedem vkládaného. Zkřížení okrajů můžeme kontrolovat při každém vkládání okraje do intervalového stromu (lze si rozmyslet, že při vkládání se úsečka porovná s oběma sousedními, pokud existují). A „nekřížící“ situace se snadno detekuje pomocí nalezení levých sousedů vkládaných okrajů (opět čas O(log T)). První případ (B v A) nastane tehdy, pokud bude sousedem levého okraje levý okraj, druhý případ (D s C) ošetří test, zdali levý soused pravého okraje vkládaného mnohoúhelníku je levý okraj téhož útvaru.

Při dosažení vrcholu, kde se jen láme okraj, stačí na první pohled otestovat zkřížení nové úsečky se sousedy. To je implementováno pomocí odebrání a vložení hrany. V praxi však nastává ještě jeden drobný problém – konkrétně zkřížení ve vrcholu okraje (D s E). Nicméně dotyky okrajů nepovažujeme za překryv (A, B a C) (toho jsme dosáhli tím, že při detekci kolizí neuvažujeme krajní body úseček a při dotyku okrajů je pravý okraj tříděn vlevo od levého).

Jak si snadno čtenář rozmyslí, řešení je analogické testu, zdali nově vkládaný mnohoúhelník je součástí jiného. Konkrétně ozkoušíme, je-li levým sousedem levého okraje nějaký pravý okraj, resp. (v případě, že se „láme“ pravý okraj) zdali je levým sousedem pravého okraje levý okraj téhož mnohoúhelníku.

Vhodnou úpravou lze tuto operaci zrychlit – konkrétně nalézt sousedy v čase O(1). Nicméně vzhledem k tomu, že prioritní fronta potřebuje na každou operaci čas O(log T), tak zpomalení vyřazením a opětovným vložením okraje nám celkovou asymptotickou složitost nezhorší.

Odebrání mnohoúhelníku ve chvíli, kdy se dostaneme se sweep-line nad něj, je triviální. Tam žádná kolize nevznikne, a je tedy potřeba jen upravit intervalový strom na absenci přislušných dvou okrajů.

Program jen implementuje výše zmíněný postup. Pokud označíme celkový počet vrcholů mnohoúhelníků N a počet stánků T, časovou náročnost můžeme celkově popsat jako O(N log T) – údržba stromu stojí O(log T) na vložení/odebrání, údržba haldy (prioritní fronty) taktéž (je třeba si uvědomit, že pokud budeme do fronty vkládat vždy jen následující zlom okraje, nebudeme v ní v žádném okamžiku mít více než O(T) prvků, podobně jako v intervalovém stromě). Paměťová náročnost je lineární vzhledem k velikosti vstupu, tedy O(N).

Program (Pascal)

Pavel Čížek

---

25-1-3 Řazení hradní stráže (Zadání)

---

První pozorování: Když si obě řady stejně přečíslujeme (obecně jakkoli přeznačíme), počet nutných přesunů se určitě nezmění. My si tedy přečíslujeme odchozí řadu tak, aby vojáci měli čísla postupně 1, … , N. Tím jsme úlohu převedli na určení nejmenšího počtu přesunů pro seřazení posloupnosti.

Druhé pozorování: Když musíme přesunout vojáka na i-té pozici, musíme přesunout také všechny, kteří stojí napravo od něj.

Všimneme si, že příchozí řada bude vždy začínat nějakou seřazenou posloupností. Označme délku nejdelší takové posloupnosti jako K. V nejhorším případě je K určitě alespoň 1.

Voják na (K+1)-té pozici stojí špatně. Kdyby nestál, měla by maximální seřazená posloupnost délku alespoň o 1 větší. Tohoto vojáka tedy musíme přesunout, a s ním i všechny vojáky napravo od něj. Dohromady tak budeme potřebovat alespoň N-K přesunů.

N-K přesunů nám zároveň stačí. Vojáci na prvních K pozicích jsou vůči sobě správně, nemusíme je tedy přesouvat. Ostatní vojáci se můžou při svém přesunu zařadit na libovolné místo, zařadí se tedy na správné místo. Pro každého z nich tak potřebujeme jen jeden přesun.

Úlohu tedy vyřešíme tak, že si nejprve přečíslujeme obě řady. Na to potřebujeme jednou projít celý vstup, což stihneme v O(N). Následně budeme procházet příchozí řadu od začátku a vždy zkontrolujeme, jestli má voják vpravo větší číslo. Tím získáme K. V nejhorším případě projdeme řadu celou, tedy opět O(N). Potřebujeme tři pole o velikosti N, takže paměťová složitost je také O(N).

Někteří z vás určovali nejen nutný počet přesunů, ale také to, kam se má každý přesouvaný voják zařadit. Těm doporučujeme číst pořádně zadání, ušetří vám to spoustu práce ;) Poznamenáme ale, že kdybychom něco takového chtěli, je nejlepší řešit úlohu pomocí binárního vyhledávacího stromu. Do něj bychom si uložili všechny vojáky ze seřazené části posloupnosti. Pak bychom do něj postupně vkládali vojáky z konce posloupnosti. Podle toho, zda přecházíme do levého, nebo pravého syna, dokážeme říct, na jakou pozici se má daný voják zařadit. Paměťová složitost by v tom případě zůstala O(N), časová složitost by vzrostla na O(N log N).

Program (C)

Jiří Setnička a Karolína „Karry“ Burešová

---

25-1-4 Útěk (Zadání)

---

Nejdříve se podíváme, jak vypadá řešení pro N=0, tedy hledání nejkratší cesty v bludišti ze startovního políčka [s_x,s_y] do cílového políčka [s_x,s_y].

K řešení budeme využívat datovou strukturu jménem fronta. Fronta funguje jako každá normální fronta. Každý prvek, který do ní přidáme, se zařadí na konec a každý prvek, který odebíráme, odebereme ze začátku. Obojí zvládneme v konstantním čase.

Algoritmus, který zde použijeme, se jmenuje prohledávání do šířky, pomocí něho zjistíme nejkratší vzdálenost každého políčka od startovního. Tyto vzdálenosti si budeme pamatovat v dvourozměrném poli D (na začátku inicializováno na -1).

Na začátku algoritmu přidáme startovní políčko do fronty a nastavíme D[s_y][s_x] = 0. Nyní, dokud fronta není prázdná, odebereme políčko p z fronty a všechna sousední políčka q, která nejsou zdmi a mají hodnotu D rovnu -1, přidáme do fronty a položíme D[q_y][q_x] = D[p_y][p_x] + 1.

Na algoritmu je vidět, že políčka zpracováváme v pořadí dle jejich vzdálenosti od startu, tedy u každého políčka nyní máme spočítanou jeho vzdálenost od startu. Pokud tento fakt hned nevidíte, tak si průběh algoritmu nakreslete do nějakého bludiště.

Časová složitost je O(velikost bludiště), každé políčko právě jednou přidáme do fronty, právě jednou jej odebereme a u každého políčka se díváme jen na 4 sousedy.

Nyní už jen zbývá vypsat, jak jsme se do cíle dostali. To můžeme jednoduše udělat tak, že si v průběhu algoritmu kromě vzdáleností navíc budeme ukládat, z jakého políčka jsme se do něj dostali. Pak jsme schopni pomocí těchto zpětných odkazů získat posloupnost políček z cíle do startu, tuto posloupnost pak stačí jen otočit a máme, co jsme chtěli.

Nyní se podívejme na variantu pro 2 ≥ N > 0. Tentokrát už nám nestačí jen přímočaře procházet bludiště, protože ještě musíme zohledňovat polohy osob.

Opět použijeme procházení do šířky, ale tentokrát nebudeme procházet jen mapu bludiště, ale něco, čemu se říká stavový prostor. Stavový prostor je nějaká množina stavů, kde z některých stavů můžeme přecházet do jiných. Například v bludišti jsou stavy jednotlivá políčka.

Každá osoba i má dané cyklické pořadí k_i políček, která navštěvuje, budeme u ní tedy rozlišovat k_i stavů.

Jednotlivými stavy pro průchod do šířky budou všechny možné pozice nás a čísla pozic osob, při kterých nestojíme na políčku zároveň s osobou. Přechody mezi stavy budou odpovídat jednomu pohybu nás a osob, při kterém se nestřetneme.

Na tomto stavovém prostoru nyní použijeme prohledávání do šířky a jsme hotovi. Ještě poznamenejme, že abychom omezili velikost stavového prostoru, nebudeme brát všechny možné pozice osob, ale že stačí vzít jen nejmenší společný násobek velikostí jejich okruhů. Na tento algoritmus se můžete podívat ve vzorovém zdrojovém kódu.

Časová složitost celého algoritmu je O(počet stavů) =O(velikost bludiště · nsn(k₁, k₂)).

Program (C++)

Karel Tesař

---

25-1-5 Algoritmus sekretářky (Zadání)

---

---

25-1-6 Sekání trávy (Zadání)

---

Nejdříve pár slov k došlým řešením. Asi nejčastější chybou bylo, že i když jste správně napsali, kdy trávník posekat lze a kdy ne, tak už jste nenapsali žádné odůvodnění, proč tomu tak je a proč to v jiných případech nelze. Občas se objevovala jen zdůvodnění pro případy, kdy to jde, v jiných řešeních zas pouze zdůvodnění, proč to v některých případech nejde.

Ke kompletnímu řešení se úloha musí rozdělit do nějakých případů a o všech se pak musí něco říct. Pokud u nějakého speciálního případu ukážeme, že řešení existuje, tak to ještě neznamená, že pro ostatní neexistuje, a naopak.

Další častou chybou bylo, že jste zapomínali na okrajové případy, kdy se řešení chová jinak. Například, pokud jeden z rozměrů je 1.

Teď už ale dost připomínek. Pojďme se raději podívat, jak to mělo být správně.

Nejdříve rozebereme případ trávníku bez kytek. Celou plochu trávníku si obarvíme jako šachovnici a všimneme si, že ať po trávníku budeme jezdit jakkoliv, tak se nám na cestě vždy po jednom budou střídat černá a bílá políčka. My chceme postupně projít všechna, každé právě jednou, a vrátit se zpět na začátek. To se nám může povést jen tehdy, pokud budeme mít stejný počet černých a bílých políček. To nastává právě, když alespoň jeden rozměr trávníku je sudý.

Nyní jsme tedy ukázali, že pro liché rozměry trávníku řešení nemůže existovat, ale o jeho existenci jsme zatím nic neřekli. Předpokládejme tedy, že alespoň jeden rozměr trávníku je sudý, a zkusme řešení zkonstruovat. Bez újmy na obecnosti budeme předpokládat, že sudá je šířka trávníku.

Pojedeme doprava až ke kraji. Pak ve sloupcích na střídačku budeme jezdit dolů a nahoru, dokud se nevrátíme na začátek. Viz křivku na obrázku. Tento postup funguje vždy, pokud máme sudou šířku. Pokud bychom měli sudou výšku, tak trávník jen otočíme. Ukázali jsme tedy, že řešení existuje, pokud máme alespoň jeden rozměr sudý.

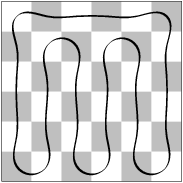
Ale pozor, to stále není všechno. Co když jeden z rozměrů trávníku bude 1? To pak naše řešení tak úplně nefunguje, protože se nemáme jak vrátit. Rozměr 1 tedy musíme vyřešit zvlášť:

• 1 ×1 posekat lze. To jen stojíme na místě.
• 1 ×2 posekat také lze. Pojedeme na sousední políčko a hned se vrátíme.
• 1 ×N, N ≥ 3 posekat nelze, protože už se nemáme kudy vrátit.

A to už je opravdu všechno, další případy pro trávník bez kytek nemáme.

Nyní k verzi trávníku s kytkami. Opět si trávník obarvíme jako šachovnici a podíváme se, ve kterých případech máme stejně černých a bílých políček (levé horní políčko vždy obarvíme na černo). Stejně jich máme, pouze pokud má trávník oba rozměry liché a kytky leží na černém políčku. V ostatních případech víme, že trávník určitě posekat nelze.

Pro liché rozměry a kytky na černém políčku zkonstruujeme obdobné řešení jako pro trávník bez kytek. Pojedeme doprava a pak na střídačku nahoru a dolů. Jediný rozdíl je, že v některé dvojici sloupců obsahující kytky budeme kličkovat, abychom obkličkovali kytky, viz obrázek.

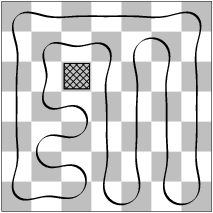
A jak poznáme, kdy kličkovat? Bude to tehdy, kdy poprvé vjedeme do sloupce s kytkami. A díky tomu, že obě souřadnice kytek mají stejnou paritu, tak před potkáním kytek budeme mít před sebou vždy lichý počet řádků, tedy před řádkem s kytkami se kličkováním dostaneme do sloupce vlevo od kytek, a po kytkách nám zbyde sudý počet řádků, tedy na konci kličkování budeme otočeni doleva.

Pokud by kytky byly v prvním sloupci, tak situaci vyřešíme zrcadlově. A pokud by byly v prvním řádku, tak si plánek otočíme.

A opět to funguje až na případy, kdy je jeden z rozměrů roven jedné. Ty zas vyřešíme zvlášť:

• 1 ×1 nedává smysl, protože se tam s kytkami nevejdeme.
• 1 ×2 řešení vždy má, jsme tam jen my a kytky.
• 1 ×3 řešení má, pokud jsou kytky vpravo.
• 1 ×N, N ≥ 4 řešení nemá, protože se nemáme jak vrátit.

A máme vše dokázáno. Jelikož nepotřebujeme znát konkrétní dráhu, tak program není třeba.

Karel Tesař

---

25-1-7 GPS log (Zadání)

---

Nejdůležitějším bodem řešení této úlohy byl algoritmus pro hledání nejdelší rostoucí vybrané podposloupnosti. Většina z vašich řešení měla kvadratickou časovou složitost. My si však ukážeme lepší řešení s časovou složitostí O(N log N).

K pojmům: Nejdelší rostoucí podposloupností posloupnosti a₁, a₂, … , a_n končící v i-tém prvku budeme rozumět posloupnost prvků a_r1, a_r2, … , a_rl takovou, že r_l = i a zároveň ∀r_j<i : r_j < r_j+1 ∧ a_rj < a_rj+1. Její délku značíme d_i.

Nejdelší klesající podposloupnost začínající v i-tém prvku je definována obdobně s tím, že musí začínat i-tým prvkem. Její délku označíme d'_i.

1. pozorování: Jestliže chceme znát délku nejdelší klesající podposloupnosti, lze obrátit pořadí prvků v poli a hledat opět rostoucí podposloupnost.

2. pozorování: Chceme-li vědět, jaký je nejdelší možný GPS log pro daný vrchol, lze ho snadno spočítat jako d_i + d'_i - 1. Stačí tedy projít vstupní pole, tuto hodnotu spočítat pro každý prvek a uložit si maximum.

Zbývá nám tedy už jen říct, jak nejdelší rostoucí podposloupnost najít. Ukážeme si nejdřív kvadratické řešení, které později zlepšíme.

Jistě platí d₁ = 1. Pro k > 1 spočítáme d_k následovně. Nechť máme nejdelší rostoucí podposloupnost končící v a_k. Zakrytím a_k dostáváme opět nějakou rostoucí podposloupnost, tentokrát končící v a_x. Její délka je d_x, tedy délka posloupnosti se zakrytým a_k je d_x + 1.

Správné x sice neznáme, lze ho však snadno najít. Víme totiž, že musí platit x < k a navíc a_x < a_k. Tedy platí d_k = max_{x<k, ax<ak} d_x + 1.

Pro vylepšení algoritmu použijme další pozorování: Jestliže máme dvě stejně dlouhé rostoucí podposloupnosti, z nichž jedna má poslední prvek menší než druhá, vždy se vyplatí použít tu s menším posledním prvkem. Zvládneme-li totiž vylepšit tu „horší“, jistě to dokážeme i pro tu „lepší“.

Stačí si tedy pro každou z možných délek posloupností držet tu nejlepší, tedy končící nejmenším možným prvkem. Označme jako m_i nejmenší hodnotu, kterou může končit i-prvková rostoucí podposloupnost z dosud prošlých prvků, a na začátku inicializujme m takto: m_i = 0 pro i = 1, jinak m_i = ∞.

Nyní postupně projdeme vstupní pole a budeme sledovat, jak se mění hodnoty m_i po zpracování nového členu.

Všimněte si nejprve, že v každém okamžiku platí, že hodnoty m_i (které jsou různé od ∞) jsou rostoucí. Když totiž umíme vytvořit rostoucí podposloupnost délky i, která končí hodnotou m_i, tak jejích prvních i-1 členů tvoří rostoucí podposloupnost délky i-1, která končí členem menším než m_i. Proto nutně m_i-1 < m_i.

Další pozorování: Pro právě zpracovávaný prvek x zjevně existuje právě jedno k takové, že m_k<x≤ m_k+1.

Co to znamená? V první řadě víme, že dosud „nejlepší“ podposloupnost délky k+1 (a větší) končila číslem větším nebo rovným x. Žádnou takovou posloupnost nemůžeme prodloužit hodnotou x, takže hodnoty od m_k+2 dále se měnit nebudou.

Podobně se nebudou měnit hodnoty od m₁ po m_k včetně. Všechny už jsou menší než x, tedy je zlepšit nedokážeme.

Změnilo se pouze to, že nyní umíme vybrat rostoucí posloupnost délky k+1, která končí hodnotou x. Nastavíme tedy m_k+1=x. Zároveň víme, že k+1 je délka nejdelší rostoucí podposloupnosti končící právě zpracovaným prvkem.

Nyní si jen stačí uvědomit, že hodnoty m_i jsou seřazeny podle velikosti, takže můžeme nalézt správné číslo k binárním vyhledáváním v čase O(log N). Potřebujeme zpracovat všech N prvků pole, časová složitost algoritmu tedy bude O(N log N).

Určit ty prvky, které máme z posloupnosti vyškrtnout je už triviální. Stačí si pro každý prvek a_i ukládat index předposledního prvku v nejdelší rostoucí podposloupnosti končící v a_i a pole proskákat až na začátek. Pro klesající část opět analogicky.

Vzorový kód je z větší části přepisem programu Martina Raszyka. Vysvětlení lineárně-logaritmické verze algoritmu je pak z větší části převzato z autorského řešení domácího kola 57. ročníku MO-P.

Program (C++)

Jan Bok

---

25-1-8 Sázíme v TeXu (Zadání)

---

Řešení úkolu 1 bylo poměrně triviální:

\chyph
{\it Poznatky získané cílevědomě
v preadolescentním věku jsou adekvátní
poznatkům pořízeným náhodně ve věku
seniorském. (Co se v mládí naučíš,
ve stáří jako když najdeš.)}
\bye

Někteří z vás neřešili \it, to jsem taktéž neřešil, neboť ze zadání nebylo úplně jasné, jestli text máte vysázet italikou, nebo romanem (latinkou).

Někteří z vás do některých slov vložili \-. To jsem penalizoval ztrátou jednoho bodu, neboť se jedná o nouzové řešení pro případ, kdy se TeXu nepovede zalámat text standardními prostředky. Představte si, že byste takhle ručně měli zalámat stostránkovou knihu.

V souvislosti s tím jsem strhával nějaké body za nepřítomnost \language\czech. Na tomto místě se musím omluvit, daleko lepší je místo \language\czech zadat \chyph (resp. \shyph pro slovenčinu) – to jsem v zadání opomenul.

Jaký je mezi tím rozdíl? \chyph nastaví kromě českých vzorů pro lámání i několik dalších parametrů, například \frenchspacing – v anglických textech se píšou za interpunkčními znaménky dvojité mezery, zato v českých textech ne.

Pokud jsem někomu za toto strhnul body, prosím, aby si stěžoval, a omyl bude napraven. Nejsem si však ničeho takového vědom.

Pokud jste se pokusili tento úkol vysázet romanem bez nastavené češtiny, zjistili jste, že na konci prvního řádku máte plže (konkrétně slimáka). Tento po správném nastavení jazyka zmizel.

Úkol 2 byl taktéž snadný. Někteří konali vlastní výzkum, jiní možná chvíli hledali na internetu, každopádně snad všichni, kdo dodali řešení, jej měli správně.

Příkaz \rm nastavuje font na roman, latinku, základní řez, jinak funguje úplně stejně jako \it nebo \bf. Ještě doporučím pozornosti čtenáře příkaz \tt, který nastaví neproporcionální strojopisné písmo (typewriter).

Jednotlivé řezy písma se v některých znacích liší. Zdrojáky je buď potřeba sázet typewriterem (\tt), nebo si musíte ohlídat znaky jako {}<>, na jejichž pozicích jsou v jiných řezech umístěny jiné, potřebnější znaky.

Úkol 3 se dal vysázet čistě na základě látky ze seriálu:

$${a^{(b-2d_c)^3} \over \sqrt{2a^{3b_1}}}
+ {}_{{}_{{}_1^2}^{{}_3^4}}
    ^{{}_{{}_5^6}^{{}_7^8}} -
\sqrt{1 + \sqrt{1 -
  \sqrt{1 + \sqrt{1 - \sqrt{
    1 + {1 - {
      1 - {1 - x\over 1 + x}
      \over 1 + {1 - x\over 1 + x}
    } \over 1 + {
      1 - {1 - x\over 1 + x}
      \over 1 + {1 - x\over 1 + x}
    }}
  }}}
}}$$

Nejvíc práce zjevně zabral druhý sčítanec – nesmyslná konstrukce z horních a dolních indexů.

Prakticky identickou konstrukci někteří řešitelé vytvořili přes \atop, což nebylo zamýšlené řešení. Výsledek však vypadal velmi podobně:

$${{1 \atop 2} \atop {3 \atop 4}}
  \atop
{{5 \atop 6} \atop {7 \atop 8}}$$

Použité primitivum se chová prakticky stejně jako \over, akorát nekreslí zlomkovou čáru.

Řešení čtvrtého úkolu jste se zhostili různě. Mnozí dodali hezký zdroják, mám z vás radost. Jiná řešení však byla odfláknutá až hrůza. Mezi nejčastější chyby patřily pomlčky (používání - místo --), uvozovky ("" místo „“) a ruční lámání řádku v případech, kdy stačilo nastavit češtinu. Také někteří z vás trestuhodně ignorovali matematický mód. Minus jedna se sází jako $-1$.

Dále jste řešili několik problémů, které jsme v zadání neprobrali, neboť buď nebylo místo, nebo si na ně nikdo nevzpomněl.

Hezké O ve složitostních vzorcích získáte jako ${\cal O}$. V matematickém módu se také dají přepínat fonty, přepínač \cal vybírá „kaligrafický“ font.

Pro stupně použijte konstrukci $90^\circ$: 90°. Vyzkoušejte také $\cdot$ a $\times$ pro různé druhy součinů (hvězdička moc hezká není) a $\ldots$ nebo $\cdots$ pro různé druhy trojteček.

Někomu se nemusí líbit výchozí nastavení formátu odstavce a stránky. To samozřejmě jde přenastavit:

• \parindent je velikost odsazení prvního řádku odstavce;
• \parskip je mezera mezi odstavci;
• \baselineskip je požadovaná vzdálenost mezi účařími jednotlivých řádků odstavce;
• pokud by po uplatnění pravidla o \baselineskip měly být boxy ve vertikálním boxu blíž k sobě (vzdálenost mezi okraji boxů) než \lineskiplimit, jsou místo toho umístěny tak, aby mezi jejich okraji byl \lineskip;
• předchozí dva body se uplatní na libovolné dva boxy, které se mají umístit do vertikálního boxu hned pod sebe, nejen na řádky odstavce.

Například můj oblíbený styl odstavců je takovýto:

\parindent 0pt
%% základní rozměr 3pt, který se smí
%% roztáhnout o 2pt a zmenšit o 1pt,
%% když je potřeba
\parskip 3pt plus 2pt minus 1pt
\baselineskip 11pt
\lineskip 1pt %% default
\lineskiplimit 0pt %% default

Na konkrétní odstavec se použijí právě ty rozměry, které jsou platné ve chvíli zpracování primitiva \par. Pokud nemá \par co vysázet, nevysází nic, ani prázdný řádek.

Na vertikální mezery rozumných velikostí můžete použít předdefinované \smallskip, \medskip a \bigskip, každý z nich je dvojnásobkem předchozího.

Pokud potřebujete, aby se každý řádek zdrojáku choval jako samostatný odstavec, použijte \obeylines. To se může hodit třeba na sazbu básní.

Na seznamy se dá použít \item{odrážka}, případně pro druhou úroveň \itemitem. Pokud byste potřebovali třetí a další úroveň odrážek, nejprve se zamyslete, jestli bude výsledek ještě stále přehledný, nebo jestli to nebude lepší vysázet jinak.

Ještě můžete chtít změnit velikost strany. Šířku a výšku strany určují rozměry \pdfpagewidth a \pdfpageheight. Šířku a výšku zrcadla (potištěné části papíru) nastavíte v \hsize a \vsize. Konečně \hoffset a \voffset mění levý a horní okraj – ten je roven tomuto rozměru plus 1in.

Tedy nastavení strany A4 s centimetrovými okraji po stranách vypadá takto:

\pdfpagewidth 210mm
\pdfpageheight 297mm
\hsize 190mm
\vsize 277mm
\hoffset -15.4mm
\voffset -15.4mm

Tolik první série. Doufám, že vás druhá série neodradí, neboť obtížnost úloh výrazně stoupla; těším se, že budu mít zase přes 30 řešení k opravování.

Jan „Moskyto“ Matějka

Menu