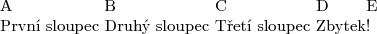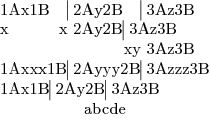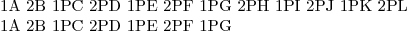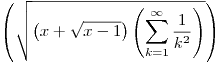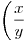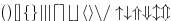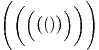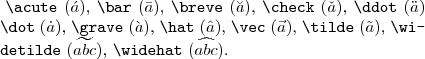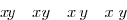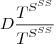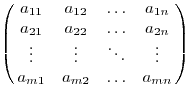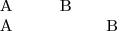Třetí série dvacátého pátého ročníku KSP
Celý leták v PDF.
I v této sérii můžete získat sladkou odměnu! Každému, kdo vyřeší
alespoň tři libovolné úlohy na plný počet bodů, pošleme čokoládu.
Zadání úloh
10. 12. 2042
Odkládat věci je snadné, proklatě snadné. Někdy kolem třicátých narozenin jsem
si řekl, že jednou sepíšu některé ze svých zážitků a zanechám v nich otisk svých
pocitů z tohoto světa. Každý rok jsem si říkal, že ještě není ta pravá chvíle,
že to přece má svůj čas.
A najednou… ani nevím jak, jsem starcem a tuším, že čas se krátí.
Když se tak zpětně ohlížím, asi jsem nikdy příliš nepřivykl tempu života.
V mládí jsem usiloval o spoustu věcí, ale vždy se mi nakonec podařilo nechat si
je proplout mezi prsty. Jednou jsem na přechodnou dobu přijal
místo u policie. Z přechodné doby se stala záležitost na celý život. Asi jsem
objevil klid, který jsem hledal. Práci jsem
trávil pochůzkami, většinou jsem lidem pomáhal s různými výtržníky a chuligány, dělal
jsem to velmi rád a po práci měl konečně klid na všechny ty věci, které mi dříve
unikaly…
Chci vyprávět o mnohém, ale začnu historkou, která mi do dnešního dne občas nedá
spát.
* * *
I když se odehrál před desítkami let, pamatuji si ten den velice dobře.
Dopoledne zajímavé nebylo, začalo velkou poradou, před kterou si náš velitel,
poručík Hamáček, neodpustil monolog o stavu disciplíny v policejním sboru,
který korunoval okázalou kontrolou toho, zda se všichni dostavili.
25-3-1 Kontrola docházky (12 bodů)
 Pro řádnou kontrolu docházky je nutno své podřízené přepočítat.
Policejní poručík Hamáček na to má svůj systém osvědčený léty služby – ve svém
notesu má N dvojic (Mi,Ki). Všechna Mi jsou po dvou nesoudělná
a 0≤ Ki<Mi. Celkový počet policistů je menší než součin všech Mi.
Pro řádnou kontrolu docházky je nutno své podřízené přepočítat.
Policejní poručík Hamáček na to má svůj systém osvědčený léty služby – ve svém
notesu má N dvojic (Mi,Ki). Všechna Mi jsou po dvou nesoudělná
a 0≤ Ki<Mi. Celkový počet policistů je menší než součin všech Mi.
Samotná kontrola probíhá v N krocích, v i-tém kroku se příslušníci srovnají
do řad po Mi osobách a poručík Hamáček následně zkontroluje, zda odpovídá
počet policistů, kteří už nemohli vytvořit celou řadu, hodnotě Ki.
Vrchní referent, strážmistr Borůvka, se stěhuje. Pomozte mu určit k takové, že
vygumováním dvojice (Mk,Kk) z poručíkova notesu umožní co největšímu počtu
kolegů mu místo porady pomoci se stěhováním.
Poručík nesmí nic poznat, tedy počty nezařazených policistů
pro zbývajících N-1 dvojic musí stále odpovídat.
Příklad: Mějme 7157 policistů, kteří se postupně řadí do řad po 12, 13 a 49
osobách. Dvojice (Mi,Ki) tedy jsou (12,5), (13,7) a (49,3). Optimálním
řešením je vygumovat dvojici (13,7). Na stanici pak musí zůstat 101 policistů.
Řešení
Po úmorném přepočítávání, připomínajícím vojenské cvičení, jsme konečně mohli usednout k poradě.
25-3-2 Zasedání u kulatého stolu (10 bodů)
Na policejní schůzi se sešlo N příslušníků policejního sboru sedících
u kulatého stolu, vzdálenost mezi každými dvěma
sousedními policisty je shodná. Schůze je dlouhá, policisté v jejím průběhu
všelijak odcházejí a přicházejí. Přítomnost policistů v pravé poledne je zadána
jakožto posloupnost N nul a jedniček, kde i-tá jednička znamená, že
policista na i-tém místě je na schůzi právě přítomen. Vaším úkolem je zjistit,
zda existuje K ≥ 3 takové, že lze vytvořit pravidelný K-úhelník, jehož
vrcholy tvoří přítomní policisté.
Příklad: Pro 12 policistů a posloupnost 111010111011 je odpověď kladná, lze
sestrojit trojúhelník nebo šestiúhelník. Pro 5 policistů a posloupnost 10111
pravidelný K-úhelník nesestrojíme. Další příklad je na obrázku (plné tečky
představují přítomné policisty):
Řešení
Po schůzi jsem se z naší tehdejší služebny ve Vlašské ulici vydal na pochůzku.
Propletl jsem se spoustou aut před Schönbornským palácem, asi se na americké
ambasádě konala důležitá recepce, a pak zahnul do spleti úzkých uliček.
V jedné velmi úzké uličce stála dost svérázně zaparkovaná černá dodávka
s japonským osazenstvem. Po zdlouhavé komunikaci, která spíš než pomocí několika
málo anglických slůvek probíhala především gestikulací, se mi podařilo domluvit,
ať mi zavolají někoho, kdo se alespoň trochu dorozumí anglicky (možná německy,
jistý jsem si naší domluvou příliš nebyl). Zatímco jsem čekal, začalo mě velmi
silně zajímat, co se nachází v těch černých pytlích v dodávce.
V tom okamžiku se ale z mé vysílačky ozval rozkaz k okamžitému přesunu
k japonské ambasádě. Má námitka, že zrovna něco zajímavého mám, byla smetena.
Prý je nutné se okamžitě postarat o bezpečnost japonského konzula. Propletl jsem
se tedy několika úzkými uličkami a za zvuku sekaček z nedalekého parku uháněl
k ambasádě.
25-3-3 Do třetice sekání (13 bodů)
V této sérii pro změnu trávník vypadá jako jeden řádek čtvercové sítě a je již
posekán, nyní je potřeba posvážet posekanou trávu. Vaším úkolem je zanalyzovat,
kolik by různé možnosti svozu stály námahy.
Máte zadáno N přirozených čísel udávajících hmotnost trávy na jednotlivých
polích a D intervalů [a..b]. Takový interval znamená, že se bude svážet
z políček a až b. Námaha pro převoz L trávy z políčka k na políčko l
je dána jako L · |k - l|. Pro každý interval určete políčko, na které se dá
všechna tráva posvážet s nejmenší celkovou námahou. Celková námaha je součet
veškeré námahy, jež byla potřeba pro svezení trávy z celého intervalu na toto
políčko.
Pokud existuje více správných políček, vypište libovolné z nich. Výpočty pro
jednotlivé intervaly jsou nezávislé, tedy množství trávy na jednotlivých
políčcích se mezi intervaly nemění. Složitost algoritmu by měla být
optimalizována pro případy, kdy je D řádově stejně velké jako N.
Příklad: (První řádek obsahuje N a D, následují hodnoty L a pak
intervaly.)
10 3
10 3 1 3 9 8 5 4 12 9
1 4
3 6
5 9
Odpovědi pro jednotlivé intervaly jsou 1 5 7.
Řešení
Před ambasádou postávalo několik lidí. Nejvíce pozornosti zde poutala žena
hovořící s jedním Japoncem, pravděpodobně oním konzulem, v jeho rodné řeči. Jemu
to zřejmě nebylo příliš příjemné.
Oslovil jsem je, abych zjistil, co se děje. Na to spustila přítomná žena dlouhý
monolog o tom, že je novinářkou, že se zabývá důležitou mezinárodní zločinnou
kauzou, že je ve veřejném zájmu, aby položila několik otázek konzulovi, že jí
japonská ambasáda odpírá právo na informace a že v této zemi obecně není
dostatečně ctěna svoboda tisku. Zatímco mi to vše tak emotivně sdělovala, jí ale
pan konzul utekl.
V okamžiku, kdy si toho všimla, trochu znejistěla, řekla něco o tom, že mi
vlastně vůbec nic není do toho, co dělá. Ona si prý jen tak postává před
ambasádou a zrovna potřebuje něco spočítat na jakési speciální kalkulačce.
A skutečně vytáhla z kabelky kalkulačku.
Ohlásil jsem stanici, že konzul je mimo nebezpečí. Trochu vzrušený hlas poručíka
Hamáčka mi sdělil, že se mám okamžitě přesunout na místo na druhém konci Malé
Strany. Prý naše jednotka bude provádět zásah.
Podařilo se mi tam dorazit v okamžiku, kdy probíhaly poslední přípravy. Zatímco
chlapi z jednotky kontrolovali zbraně, vyprávěl poručík Hamáček svým skoro
otcovským hlasem o tom, jak mu jeho pečlivá příprava jednou zachránila život při
střetu se členy jednoho nebezpečného mezinárodního gangu.
25-3-4 Zločinná záležitost (10 bodů)
Ve špinavých vodách mezinárodního zločinu je obzvláště důležitá organizace,
typickým příkladem zločinu je výroba něčeho ilegálního. Výroba probíhá ve fázích
a obvykle na více než jednom místě. Převoz z jednoho místa na druhé je
nejkritičtější částí výrobního procesu, proto je potřeba počet převozů mezi
výrobními místy minimalizovat.
V této úloze budete mít na vstupu popsán výrobní proces ve dvou továrnách. První
řádek obsahuje čísla N a M, kde N udává počet výrobních fází a M počet
závislostí mezi nimi. Druhý řádek vstupu obsahuje N hodnot, kde i-tá hodnota
je 1, pokud má i-tá fáze probíhat v první ilegální továrně, a 2 v případě, kdy
má probíhat ve druhé továrně. Následuje M řádků obsahující dvojice a, b,
které značí, že fáze b může proběhnout až tehdy, když byla provedena fáze a.
Určete pořadí fází výrobního procesu tak, aby každá fáze proběhla až poté, co
jsou provedeny všechny fáze, na kterých je závislá, a aby počet převozů mezi
výrobními místy byl minimální. Převoz je nutný vždy, když po fázi probíhající
v továrně 1 bezprostředně následuje fáze v továrně 2, nebo naopak. (Můžete
předpokládat, že řešení existuje.)
 Lehčí varianta (za 6 bodů): Nabízíme k řešení i jednodušší variantu úlohy, kde všechny
fáze probíhají v jediné továrně.
Lehčí varianta (za 6 bodů): Nabízíme k řešení i jednodušší variantu úlohy, kde všechny
fáze probíhají v jediné továrně.
Příklad:
7 9
2 2 1 1 1 2 1
2 1
2 5
3 2
3 4
4 1
4 5
4 7
5 6
6 7
Potřebujeme alespoň 4 převozy. Výroba může proběhnout takto – začneme v první
továrně, provedeme v ní fáze 3 a 4, pak se přesuneme do druhé továrny a
provedeme fáze 2 a 1. Následují fáze 5 v první továrně a 6 v druhé továrně,
končíme po čtvrtém převozu v první továrně fází 7.
Řešení
Už se nepamatuji, jaké zločince tam naše jednotka očekávala. Každopádně, po
pompézním vyražení dveří a sražení k zemi všech přítomných osob zjistili
ozbrojení kolegové, že se jim podařilo zneškodnit všehovšudy tři zaměstnankyně
jakéhosi asijského bufetu. Vydal jsem se tedy zase zpátky k dodávce, třeba tam
ještě něco zajímavého bude.
Nešel jsem ani pět minut a opět mě volali vysílačkou. K dodávce se asi jen tak
nedostanu. Měl jsem přivést japonského chlapce v černém tričku a modrých riflích
s velkým fotoaparátem. Spatřen prý byl na nedalekém náměstí.
Na náměstí skutečně ještě byl. Působil nesmírně zmateně. V okamžiku, kdy mě
zahlédl, ke mně natáhl ruku s peněženkou. Netušil jsem, co tím zamýšlí, zda to
jsou jeho doklady, či nějaká lest k tomu, aby mohl následně utéci. Každopádně
jsem k němu přistoupil, pokusil se na něj usmát, něco mu říct a raději jej
chytil jemně za rameno a pro jistotu chytil i onen důležitý foťák, aby jej v té
nervozitě ještě nerozbil.
V tom se zezadu přiřítila opět ona milá novinářka a vzala z jeho ruky peněženku.
Povídala, že to je její peněženka a že si to klidně mohu zkontrolovat. Učinil
jsem tak a dal jí podržet chlapcův fotoaparát. Dřív, než jsem stihl zareagovat,
z něj vyndala paměťovou kartu. V duchu jsem si zanadával, věděl jsem, že tyhle
novinářky jsou dost mazané a šikovné na to, abych tu kartu už nikdy neviděl
a radši se tvářil, že jsem si toho nevšimnul. (Krátce před tím jsem udělal ještě
jeden průšvih, a kdyby se k tomu přidalo, že jsem si nechal před nosem vzít
paměťovou kartu, opravdu by mi to neprospělo.)
Pak jsem chlapce odvedl k nám na stanici. Na chodbě zrovna postával jeden
z vyšších velitelů pražské policie, u nás na stanici jsem jej viděl asi podruhé.
Vzal si ode mě chlapcův fotoaparát a řekl mi, ať se postarám o chlapce a najdu
jeho rodiče.
Vzal jsem jej k nám do kanceláře, zdál se být hodně zaujat prací naší
sekretářky. Zrovna přerovnávala přílohy ke spisům, především grafy.
25-3-5 Histogram (9 bodů)
Jedním z četně používaných typů grafů je histogram. Histogram je, jak praví
Wikipedie, grafické znázornění distribuce dat pomocí sloupcového grafu se
sloupci stejné šířky. Máte zadán histogram
jakožto posloupnost N přirozených čísel udávajících výšky sloupců, šířka
sloupců je jednotková. Určete obsah největšího obdélníka rovnoběžného s osami,
který lze do grafu umístit tak, že celá jeho plocha leží na sloupcích
histogramu.
Příklad: Pro 7 sloupců a výšky 3 6 7 4 2 3 1 je výsledný obsah 12. Existují
hned 4 různé obdélníky s tímto optimálním obsahem. Další příklad
s jednoznačným řešením je na obrázku:
Řešení
Chlapec mi naštěstí dal kartičku pro podobné případy. Mimo jiné se na ní
nacházelo číslo na japonskou ambasádu. Během telefonátu s ambasádou přišel
velitel, jemuž jsem předával foťák. Byl dost naštván, že ve fotoaparátu nebyla
paměťová karta a jestli o tom něco nevím, samozřejmě jsem odpověděl, že nikoliv.
Sekretářka ambasády se při našem telefonátu musela dobře bavit.
Domluvili jsme se, že jim chlapce přivedu. Předal jsem jej vrátnému, ten člověk
to asi s dětmi uměl lépe. Už když se pozdravili, objevil se na chlapcově tváři
úsměv. Na jeho stole jsem dokonce zahlédl nějakou knihu s kresbou draka a
princezny. Chlapec byl určitě v dobrých rukou.
25-3-6 Rytíř a princezny (10 bodů)
 Rytíř v dalekém království se vydal na hrdinnou výpravu. Trasa jeho
výpravy vypadá jako N polí uspořádaných do řádku. Na každém poli se nachází
buď drak, který má u sebe H zlatých mincí, nebo princezna, která má koeficient
krásy K. Rytíř se pohybuje při své výpravě z prvního políčka na poslední a je
dostatečně silný na to, aby zabil kteréhokoliv draka po cestě. Je jeho volbou,
zda draka zabije a získá mince, či jej obejde a ponechá drakovi život i mince.
Rytíř v dalekém království se vydal na hrdinnou výpravu. Trasa jeho
výpravy vypadá jako N polí uspořádaných do řádku. Na každém poli se nachází
buď drak, který má u sebe H zlatých mincí, nebo princezna, která má koeficient
krásy K. Rytíř se pohybuje při své výpravě z prvního políčka na poslední a je
dostatečně silný na to, aby zabil kteréhokoliv draka po cestě. Je jeho volbou,
zda draka zabije a získá mince, či jej obejde a ponechá drakovi život i mince.
V okamžiku, kdy přijde k princezně o kráse K, nastávají dvě možnosti. Pokud
již rytíř zabil alespoň K draků, princezna se do něj zamiluje a chce si jej
vzít. Rytíř není schopen odmítnout a jeho výprava končí. Pokud rytíř zabil menší
počet draků, prohodí pár zdvořilých slov s princeznou a pokračuje ve výpravě.
Na posledním políčku sídlí princezna, kterou rytíř miluje. Pro zadanou trasu
výpravy určete, zda je možné získat princeznu na posledním poli. Pokud ano,
vypište seznam zabitých draků tak, aby rytíř získal nejen princeznu na posledním
poli, ale i co nejvíce zlatých mincí.
Tato úloha je praktická a řeší se ve vyhodnocovacím systému
CodEx.
Přesný formát vstupu a výstupu, povolené jazyky a další technické informace
jsou uvedeny v CodExu přímo u úlohy.
Řešení
Konečně jsem se mohl vrátit na místo dodávky, ta už tam přirozeně nebyla. Místo
jsem prohledal. V nedalekém průchodu jsem objevil svého starého kolegu a
přítele, říkejme mu Jan. Jan se tam bavil s dalším mužem, pravděpodobně
Japoncem. K mé smůle si mne všimli a Japonec se dal na útěk. Rozběhl jsem se za
ním, ale Jan se mi postavil do cesty.
Měl s sebou obří brašnu na spisy. Vypadal opravdu vyděšeně, říkal jen:
„Prosím, nech mě odejít. Nikdy jsme se tady neviděli.“
Tak jsem to i udělal. Být to kdokoli jiný, okamžitě jej zatýkám a zabavuji tyto
spisy. Toto ale byl Jan – můj nejlepší přítel, kterému jsem vděčil opravdu za
mnoho. V dalších částech svého vypravování se k tomu snad ještě dostanu.
* * *
O kauze toho později proniklo mnoho ven. Došlo i k sérii vražd, asi 2 měsíce po
dni, o němž jsem vyprávěl. O 20 let později se mi podařilo dokonce dostat
k odtajněným spisům GIBS a ÚOOZ. Vyšetřovalo se velmi důkladně, ale nakonec byl
případ uzavřen pro nedostatek důkazů.
25-3-7 Zkratky (7 bodů)
 Svět je plný zkratek, nejen těch policejních. V této úloze máte zadáno
nejvýše 10 zkratek o nejvýše pěti písmenech a slovo délky L. Vaším úkolem je
rozhodnout, zda lze slovo sestavit ze zadaných zkratek. Zkratky je možno
spojovat za sebe a jednu zkratku lze použít i opakovaně.
Svět je plný zkratek, nejen těch policejních. V této úloze máte zadáno
nejvýše 10 zkratek o nejvýše pěti písmenech a slovo délky L. Vaším úkolem je
rozhodnout, zda lze slovo sestavit ze zadaných zkratek. Zkratky je možno
spojovat za sebe a jednu zkratku lze použít i opakovaně.
Příklad: Pokud bychom jako zkratky měli oblíbenou čtveřici sus,
usu, sss, Ssu a ještě pro obohacení su. Pak slovo
Ssusss postavit půjde, slovo sususu také a rovnou dvěma způsoby, ale
slova ssss nebo susSus už nepostavíme.
Řešení
S Janem jsme překvapivě zůstali v kontaktu. Říkal, že se svou nerozvážností
dostal do obřího průšvihu a šlo mu o život. Domluvili jsme se, že další
informace si raději nechá pro sebe. Mnoho času jsem přemítal nad tím, jaká je
cena přátelství. Trápila mě otázka, zda právě tyto spisy nemohly případ
rozuzlovat a třeba i zabránit dalšímu krveprolití…
Ke zpovědi policisty se dostal
Lukáš Folwarczný
25-3-8 Tabulatika (13 bodů)
 Upozornění: Přesný vzhled vysázených konstrukcí je v PDF
verzi! Ve webové verzi mohou být různé nepřesnosti, zvláště u vzhledu
vysázených vzorců. Pokud si tedy chcete být jisti tím, jak něco vypadá,
sáhněte prosím po verzi v PDF.
Upozornění: Přesný vzhled vysázených konstrukcí je v PDF
verzi! Ve webové verzi mohou být různé nepřesnosti, zvláště u vzhledu
vysázených vzorců. Pokud si tedy chcete být jisti tím, jak něco vypadá,
sáhněte prosím po verzi v PDF.
Třetí díl seriálu o TeXu bude snad méně děsivý než druhý. Nebojte,
budeme se věnovat „jenom“ tabulkám, pokročilé matematice a podrobnostem
sazby odstavců.
Sazba na tabulátory
Nejjednodušší tabulky můžeme sázet jednoduchým způsobem. Následující konstrukcí
rozdělíme stránku na 3 stejně široké sloupce a pak do nich sázíme řádky:
\settabs 3\columns
\+Sloupec 1&Sloupec 2&Sloupec 3\cr
\+&Jen druhý\cr
\+První&&a třetí\cr
\+Vykřičník je ve čtvrtém sloupci~-- mimo&&&!\cr
\+První sloupec je příliš dlouhý&
a druhý se přesází přes něj.\cr
\+Mezery za \&& se ignorují.\cr
\+\hfill Tento řádek&\hfill je zarovnán
&\hfill na pravý okraj.&\cr
Ukončení tabulky se nijak zvlášť neřeší.
Poznámka: Důvod, proč zde má \hfill najednou dvě L, vysvětlíme
v tomto díle seriálu v kapitole o různých typech lepidla.
Nelíbí se vám stejně široké sloupce? Vymyslete si vzorový řádek, podle kterého
TeX nastaví šířky sloupců:
\settabs\+První sloupec &Druhý sloupec
&Třetí sloupec &Zbytek&\cr
\+A&B&C&D&E\cr
\+První sloupec &Druhý sloupec
&Třetí sloupec &Zbytek&!\cr
Vzorový řádek se nezobrazí, jen se podle něj nastaví šířka sloupců.
Úkol 1 [2b]
Vysázejte pomocí tabulátorů tuto jednoduchou tabulku z knihy jízd:
Správně odsazený zdrojový kód
Tabulátory vůbec nemusí být extra pevné. Můžeme zrušit všechny
tabulátorové pozice vpravo od aktuální „buňky“ příkazem \cleartabs.
A pokud použijeme mezi \+ a \cr znak & na místě, kde ještě
není definovaná tabulátorová pozice, tak se ta pozice jednoduše nadefinuje
právě na ono místo.
Víc asi ukáže příklad:
\cleartabs
\+{\bf if} $x<0$: &{\bf if} $x<-1000$:
&{\it print} \uv{$x$ je echt záporné}\cr
\+&{\bf else}:
&{\it print} \uv{$x$ je trochu záporné}\cr
\+{\bf else}: &\cleartabs{\bf if} $x>0$:
&{\it print} \uv{$x$ je kladné}\cr
\+&{\bf else}: &{\it print} \uv{$x$ je nula}\cr
Tabulky
Při sazbě na tabulátory je potřeba odhadnout, který sloupec bude jak dlouhý,
a podle toho nastavit šířku sloupců. Také pokud chcete tabulku s orámováním,
nemáte moc rozumných možností. TeX však nabízí mocnější nástroj než sazbu na
tabulátory – primitivum \halign.
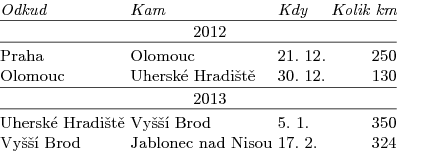
Tabulku z úkolu 1 vysázíme primitivem \halign takto:
\halign{
# \hfil&# \hfil&# \hfil& \hfil#\cr
\it Odkud&\it Kam&\it Kdy&\it Kolik km\cr
Praha&Olomouc&21. 12.&250\cr
Olomouc&Uherské Hradiště&30. 12.&130\cr
Uherské Hradiště&Vyšší Brod&5. 1.&350\cr
Vyšší Brod&Jablonec nad Nisou&17. 2.&324\cr
}
Tabulka se skládá z jednotlivých řádků oddělených od sebe značkou \cr.
Buňky se od sebe oddělují znakem & (nebo jiným znakem kategorie 4 – alignment).
První řádek obsahuje vzor. V každé buňce musí být znak # (kategorie 6 – parameter)
právě jednou (jinak vám TeX vynadá), jinak může být vzorem prakticky
libovolný kus TeXu, který se dá použít uvnitř hboxu (třeba \bye není
povolený příkaz). Buňky se pak sází tak, že se v příslušném vzoru nahradí
výskyt znaku # za obsah buňky.
Dejte si pozor na mezery – mezery za & se ignorují, mezery před & se neignorují.
Tabulky a boxy
Při sazbě tabulky si TeX zjistí pro každý sloupec, jak bude široký, a podle
toho nastaví šířku všem jeho buňkám. Každá buňka tabulky je separátní hbox
široký právě tak jako celý sloupec. Pokud nechcete mít ošklivě roztažené mezery
v textu, vložte na vhodné místo \hfil-y, vizte příklad výše.
Očárovaná tabulka
Potřebujete-li do tabulky vložit vodorovnou čáru (nebo libovolný jiný
materiál), využijte prostředí \noalign. Tím začne vertikální box šířky
přesně takové, jak je široká celá tabulka:
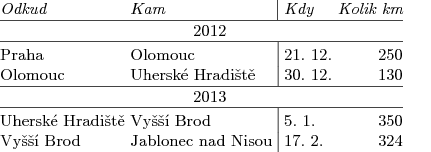
\halign{
\strut# \hfil&# \hfil&# \hfil& \hfil#\cr
\it Odkud&\it Kam&\it Kdy&\it Kolik km\cr
\noalign{\hrule\smallskip\line{\hfil
2012 \hfil}\smallskip\hrule\smallskip}
Praha&Olomouc&21. 12.&250\cr
Olomouc&Uherské Hradiště&30. 12.&130\cr
\noalign{\hrule\smallskip\line{\hfil
2013 \hfil}\smallskip\hrule\smallskip}
Uherské Hradiště&Vyšší Brod&5. 1.&350\cr
Vyšší Brod&Jablonec nad Nisou&17. 2.&324\cr
}
Potřebujeme-li i svislé čáry, je náš úkol o poznání složitější. TeX totiž
vkládá každý řádek tabulky samostatně do stránkového vboxu jako jednotlivé
hboxy. Takže mezi ně vloží \lineskip nebo \baselineskip. Proto je
musíme vypnout a výšky řádků nastavit explicitně. Na vypnutí lineskipů
„pořádně a důkladně“ použijte makro \offinterlineskip, které myslí i
na zběsilé okrajové případy.
Aby byl každý řádek stejně vysoký, je potřeba do něj vložit vzpěru. Jinak by
sazba vypadala ošklivě. K tomu se hodí makro \strut, které je v Plain
TeXu definováno přibližně takto:
\def\strut{\vrule height 8.5pt
depth 3.5pt width 0pt\relax}
{\offinterlineskip
\def\higher{\vrule height 11pt
depth 3.5pt width 0pt\relax}
\halign{%
\strut# \hfil&# \hfil\vrule\ &# \hfil& \hfil#\cr
\it Odkud&\it Kam&\it Kdy&\it Kolik km\cr
\noalign{\hrule\smallskip\line{\hfil
2012 \hfil}\smallskip\hrule}
\higher Praha&Olomouc&21. 12.&250\cr
Olomouc&Uherské Hradiště&30. 12.&130\cr
\noalign{\hrule\smallskip\line{\hfil
2013 \hfil}\smallskip\hrule}
\higher Uherské Hradiště&Vyšší Brod&5. 1.&350\cr
Vyšší Brod&Jablonec nad Nisou&17. 2.&324\cr
}}
Ještě se vám můžou hodit dvě tabulkové operace: \omit na začátku buňky
dočasně nahradí vzor pro tuto buňku za prosté #.
Místo & v běžném řádku můžete použít \span. V tu chvíli se
příslušné dvě buňky spojí. To, co bylo před \span-em, se vloží na místo
prvního #, a to, co je za \span-em, se vloží na místo druhého
#.
{\offinterlineskip
\halign{
\strut1A#1B\hfil\vrule&\ 2A#2B\hfil\vrule
&\ 3A#3B\hfill\cr
x&y&z\cr
\omit\strut x x&y\span z\cr
\omit\strut\hfil x\span\omit y&z\cr
xxx& yyy& zzz\cr
x\span y\span z\cr
\omit\span\omit\span\omit
\strut\hfil abcde\hfil\cr
}}
Podrobnosti o tom, jak se vlastně TeX v tabulkách chová, si najděte
v TeXbooku v kapitole 22 (nebo
v TBN (Petr Olšák: TeXbook naruby, Konvoj Brno 2001 (2. vydání), ISBN 80-7302-007-6)
v kapitole 4) – překračuje to rámec tohoto seriálu.
Úkol 2 [6b]
Definujte makra pro sazbu výsledkové listiny KSP. Zdroják výsledkovky pak může
vypadat například takto:
\vysledkovka{
\radek 1. Petr Pilný (GABCD; 4; 7):
12 7 - 4 9 5 - 7: 49,4 69,3
\radek 2. ...
}
Pokud se vám nelíbí současný desing naší výsledkovky, navrhněte lepší a přehlednější.
Poznámka: Pokud byste potřebovali tabulku ne po řádkách, ale po sloupcích,
zkuste \valign. Funguje to stejně jako \halign, jenom otočeně.
Periodická hlavička
Zdvojíte-li v hlavičce na nějakém (nejvýše jednom) místě &,
říkáte tím TeXu: „Zde začíná periodická část hlavičky.“ Tedy pokud by
v nějakém řádku došly vzory pro buňky, tak začne recyklovat vzory od &&
dál:
\halign{1# & 2# && 1P# & 2P# \cr
A&B&C&D&E&F&G&H&I&J&K&L\cr
A&B&C&D&E&F&G\cr
}
Tolik k tabulkám.
Matematické závorky
Ve druhé části poněkud rozkouskovaného třetího dílu se budeme věnovat
složitějšímu využití matematického módu.
Složité vzorce jsou často různě zběsile vysoké a jedna velikost závorek
nestačí. Prohlédněte si příklad:
TeX si umí určit velikost závorek sám, jen je potřeba mu říct, která patří ke
které. Používají se k tomu primitiva \left a \right, kterými se
označí příslušné závorky:
$$\left(\sqrt{
\left(x + \sqrt{x - 1}\right)
\left(\sum_{k=1}^\infty {1 \over k^2}\right)
}\right)$$
TeX sám zvolí velikost závorek takovou, aby byly vhodně vysoké. Pokud byste
potřebovali, aby se jedna ze závorek nezobrazila, použijte místo ní tečku:
\left({x\over y}\right.
Typů závorek je hrozná spousta, Plain určitě zná tyto:
$$()[]\{\}\vert\Vert\lceil\rceil
\lfloor\rfloor\langle\rangle
\backslash/\uparrow\downarrow
\Uparrow\Downarrow\updownarrow\Updownarrow$$
Pokud byste čirou náhodou potřebovali použít jiné závorky, konzultujte
TeXbook, kapitolu 17 a následující (nebo TBN, kapitolu 5).
Může se vám však stát, že potřebujete jinak velkou závorku, než vám dá TeX.
V takovém případě jsou pro vás připraveny varianty \big, \bigg,
\Big a \Bigg:
$\Bigg(\bigg(\Big(\big(()\big)\Big)\bigg)\Bigg)$
Zákulisí matematické sazby
Ani celý rozsah seriálu by zdaleka nevystačil na vyložení sazby matematiky
v celé její kráse a síle. Donald Knuth na to v TeXbooku vynaložil přes
60 stran. Naznačíme si však některé principy, které by vám při pokročilé sazbě
neměly zůstat utajeny.
TeX umí velmi sofistikovaně rozložit mezery do matematického vzorce, pokud
ví, jakého typu je která část vzorce. Rozlišuje těchto 13 typů:
| Ord | Standardní „atom“ | x či 1 |
| Op | Velký operátor | ∑ či ∫ |
| Bin | Binární operátor | + či - |
| Rel | Relace | = nebo < |
| Open/Close | Začátek/konec závorky | (/), [/], … |
| Punct | Interpunkce | čárka, středník |
| Inner | Složitější konstrukce | zlomek |
| Over/Under | Atom s čárou nad/pod | , x |
| Acc | Atom s „diakritikou“ | xˆ, x→ |
| Rad | Cosi pod odmocninou | √2 |
| Vcent | Výstup z \vcenter | |
Poznámka: PlainTeX má v matematice definována tato diakritická znaménka:
Používají se stejným způsobem jako nematematická.
Poznámka: \vcenter je explicitní vbox v matematickém módu, který je
stejně vysoký jako hluboký, takže se vysází centrovaný na osu. Vůbec,
matematika se sází ne na účaří, ale na pomyslnou vodorovnou osu, neboť
vzorce jsou často takto symetrické. Ale toho už jste si jistě všimli.
Mezi jednotlivými kategoriemi je pak definována tabulka, která určuje, kam
patří jak velká mezera. Tato tabulka je pro drtivou většinu použití dostačující.
Pokud vám připadá, že TeX nějakou mezeru určil chybně, zkuste označit atomy
v jejím okolí jejich typem. K tomu použijte \mathord, \mathop,
\mathbin, \mathrel, \mathopen, \mathclose,
\mathpunct a \mathinner. Zbytek typů se značí automaticky a nelze
je označit ručně.
Pokud selže i označení atomu vhodným typem, můžete použít mezery různých
velikostí – \,, \; nebo \!:
$$x\!y\quad xy\quad x\,y\quad x\;y$$
Matematický mód se dělí na několik dílčích módů. Všimněte si, jak se vysází
různé výrazy na různých místech – $$\sum$$, $\sum$,
$x^{\sum}$ či $x^{x^{\sum}}$. Nejde jen o velikost, ale také
o umístění indexů a rozložení mezer.
Ony dílčí módy jsou D, T, S a SS: „display“, „text“, „script“ a
„scriptscript“ uvedené ve stejném pořadí jako v předchozím odstavci.
Chcete-li si vyzkoušet víc magie okolo módů, poradím primitivum \mathchoice:
\def\te{{\mathchoice{D}{T}{S}{SS}}}
$$\te {\te^{\te^\te} \over \te^{\te^\te}}$$
Nebo můžete vynutit konkrétní mód použitím \displaystyle,
\textstyle, \scriptstyle a \scriptscriptstyle.
Tabulkové konstrukce v matematice
Plain TeX definuje některé maticové konstrukce:
$$\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
a_{21}&a_{22}&\ldots&a_{2n}\cr
\vdots&\vdots&\ddots&\vdots\cr
a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$
Použití je obdobné jako u tabulek, jen nemusíte definovat vzorový řádek. Matici
bez závorek můžete získat použitím \matrix. A na matici s okraji je
definováno makro \bordermatrix (vyzkoušejte sami).
Úkol 3 [3b]
Vysázejte tento vzorec:
Sázíme odstavec
Další kousek třetího dílu věnujeme podrobnějšímu náhledu na algoritmus lámání
odstavce.
Když se na vstupu objeví něco, co by mělo začít odstavec (znak,
\indent (Primitivum \indent explicitně započne odstavec;
\indent\indent si vyžádá dvojité odsazení (možno opakovat
vícekrát pro vícenásobné odsazení). A konečně explicitní začátek odstavce bez
odsazení vynutíte primitivem \noindent.), …), zkontroluje TeX
několik věcí. Na začátek horizontálního boxu, který
bude později zalámán na jednotlivé řádky v odstavci, se vloží prázdné místo
velikosti \parindent (pokud nebyl odstavec zahájen pomocí příkazu
\noindent).
Pak se expanduje \everypar, což je seznam tokenů
(pseudomakro), které se má vložit na začátek každého odstavce. Přiřazuje se do
něj zavoláním \everypar={něco}. Standardně je prázdný.
Pak se do horizontálního boxu postupně vkládají znaky, dokud se neobjeví \par.
Nyní se na úplný konec boxu vloží prázdné místo velikosti \parfillskip
(standardně \hfil). Pak se TeX pokusí zalámat odstavec s přihlédnutím
k nastavenému tvaru odstavce. Každý řádek musí obsahovat nejprve prázdné místo
velikosti \leftskip, pak příslušný kus odstavce a pak prázdné místo
velikosti \rightskip. Dohromady je vždy široký přesně \hsize.
Poznámka: Pro zjednodušení nyní vynecháváme možnost úpravy tvaru odstavce
primitivem \parshape a nastavením \hangindent a
\hangafter, které nás čekají v další sérii.
TeX se pokouší zalámat odstavec celkem třikrát. Nejprve v mezerách mezi
slovy. Pokud mu to nejde, zkusí rozdělit slova podle pravidel pro dělení slov.
Pokud se mu ani toto nepovede, zkusí nepatrně roztáhnout mezery a rozdělit
slova. Pokud selže i poslední pokus, vyhlásí chybu, nechá nějaký řádek přetéct
a vykreslí slimáka.
Lámání odstavce probíhá najednou, TeX se snaží, aby nebyl jeden řádek ošklivě
stažený a hned ten další ošklivě roztažený – má nějaký základní smysl pro estetiku.
Nicméně když při druhém a třetím pokusu dělí slova, musí vědět, kde všude může
dělit, jinak může odstavec vyjít zbytečně ošklivě. To je ten zásadní důvod,
proč jsem v první sérii všem řešitelům bez \language\czech strhával body.
Přesný algoritmus včetně všech podrobností, které jste nikdy nechtěli znát,
najdete v TeXbooku v kapitole 14 (nebo v TBN v kapitole 6).
Lepidlo
Prázdné místo je v sazbě důležitá věc. Někdy se s nadsázkou dokonce říká, že
celá typografie je věda o prázdném místě. V poslední části tohoto dílu seriálu se
naučíme pracovat s jeho roztažností.
TeX nahlíží na prázdné místo jako na kusy „lepidla“, které se může různě
roztahovat a smršťovat. Český odborný název je „výplněk“. Je několik druhů
roztažnosti:
Pevný výplněk svoji velikost nemění. Je vždy stejně velký:
\hbox{A\hskip 2cm\relax B}
Omezeně roztažitelný výplněk má základní velikost a meze, kam až se může roztáhnout.
\hbox to 15mm{A\hskip 2cm plus 1cm minus 1cmB}
\hbox to 25mm{A\hskip 2cm plus 1cm minus 1cmB}
Roztažnost nemusí být na obě strany stejná: 10mm plus 5mm minus 3mm
Nekonečně roztažitelný výplněk má základní velikost a jinak se může
roztáhnout neomezeně podle potřeby.
\hbox to 5cm{A\hskip 2cm plus 1fil\relax B}
\hbox to 1cm{A\hskip 2cm minus 1fil\relax B}
Nekonečných roztažností jsou tři druhy: fil, fill a
filll. Čím víc L, tím agresivněji se roztahuje.
Jeden výplněk je nuda. Co kdyby se někde potkalo více výplňků? Když TeX
skládá box, u kterého dopředu neví, jak bude velký, tak se vůbec roztažností
neřídí. Ideální je vždycky, když se nic natahovat nemusí, takže použije vždy
pouze základní velikost. V opačném případě má nařízeno, jak musí být výsledný
box velký, a musí se do něj chtě nechtě vejít.
Pokud je nutné roztahovat a stahovat bílé místo, TeX určí správné mezery
přibližně takovýmto algoritmem:
- Zjistí, jakou velikost by měl box, kdyby se použily základní velikosti. Určí
rozdíl mezi požadovanou a základní velikostí. Je-li rozdíl kladný, bude nás
dále zajímat pouze kladná roztažnost; je-li rozdíl záporný, budeme řešit pouze
zápornou roztažnost. Tento rozdíl si označme jako w.
- Sečte povolenou roztažnost přes celý box – zvlášť omezenou a zvlášť každý
druh nekonečné roztažnosti.
- Vybere nejagresivnější roztažnost, která je nenulová, a tou se bude zabývat.
- Rozpočítá w mezi všechny výplňky, které přispěly do roztažnosti, podle
poměru, ve kterém přispěly.
Vizte příklad:
\hbox{\vrule
\hbox to 6cm{\strut%
\hskip 5mm plus 3cm
\vrule width 1cm
\hskip 1cm plus 1cm minus 1cm
\vrule width 1cm
\hskip 5mm minus 2cm
}\vrule}
Vnitřní hbox má být široký 6 cm. Základní šířka boxu vyjde 0,5+1+1+1+0,5=4 cm,
w=6-4=2 cm. Zajímá nás tedy kladná roztažnost. Čáry se neroztahují, řešíme
tedy jen skipy: 3+1+0=4 cm, jiná roztažnost není.
Potřebujeme tedy rozdělit 2 cm mezi první a druhý skip v poměru 3 : 1,
tedy prvnímu skipu se přidělí 15 mm a druhému 5 mm. Box se tedy vysází, jako
by byl zadán takto:
\hbox to 5cm{\hskip 20mm\vrule width 1cm
\hskip 15mm\vrule width 1cm\hskip 5mm}
Druhý příklad bude složitější:
\hbox{\vrule
\hbox to 5cm{%
\hskip 5mm plus 1fil
\vrule width 1cm
\hskip 1cm plus 2cm minus 1cm
\vrule width 1cm
\hskip 5mm minus 1fil
}\vrule}
Základní šířka boxu je 5 cm, obsah má základní šířku 4 cm, w=1 cm. Celková
kladná roztažnost je 2 cm + 1 fil, takže nás zajímá jen 1 fil. Prvnímu skipu
se tedy přidělí celý 1 cm.
Rozmyslete si, co se stane, když:
- poslední hskip nebude mít
minus 1fil, ale plus -1fil;
- první hskip bude mít
plus 1fill;
- bude hbox
to 4cm nebo to 3cm.
Nyní je čas na důležitou poznámku. Roztažnost mají pouze skipy (výplňky), mezi
které se počítají i běžné mezery mezi slovy. Všechno ostatní (boxy, čáry) má
pevnou velikost, jakmile je to vytvořeno. Není možné vytvořit box, jehož
rozměry by byly pružné podle jeho okolí. Najděte si třeba ve své sazbě řádek
s hodně roztaženými mezerami a část toho řádku uzavřete do hboxu. Všimněte si,
co se stane s mezerami, a zkuste si rozmyslet, proč to tak může být.
Připomínám, že je nanejvýš vhodné si vyzkoušet práci s tabulkami i pokročilou
matematikou na uvedených příkladech. Zkuste je dál modifikovat a hrát si
s nimi, ať si to všechno důkladně zažijete. Příště budeme konečně programovat.
Úkol 4 [2b]
Vymyslete nastavení parametrů odstavce tak, aby se zarovnal na střed.
Řešení nemusí být univerzální,
stačí, aby se zadaný odstavec povedlo vysázet v běžném případě. Nemusíte řešit
okrajové případy, kdy je odstavec extrémně krátký apod.
A to bude ze třetí série vše. Těším se na vaše řešení.
Jan „Moskyto“ Matějka
Řešení
 Pro řádnou kontrolu docházky je nutno své podřízené přepočítat.
Policejní poručík Hamáček na to má svůj systém osvědčený léty služby – ve svém
notesu má
Pro řádnou kontrolu docházky je nutno své podřízené přepočítat.
Policejní poručík Hamáček na to má svůj systém osvědčený léty služby – ve svém
notesu má 
 Lehčí varianta (za 6 bodů): Nabízíme k řešení i jednodušší variantu úlohy, kde všechny
fáze probíhají v jediné továrně.
Lehčí varianta (za 6 bodů): Nabízíme k řešení i jednodušší variantu úlohy, kde všechny
fáze probíhají v jediné továrně.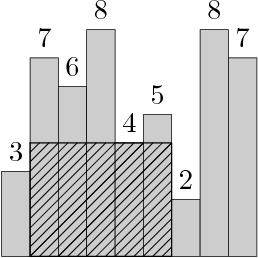
 Rytíř v dalekém království se vydal na hrdinnou výpravu. Trasa jeho
výpravy vypadá jako
Rytíř v dalekém království se vydal na hrdinnou výpravu. Trasa jeho
výpravy vypadá jako  Upozornění: Přesný vzhled vysázených konstrukcí je v PDF
verzi! Ve webové verzi mohou být různé nepřesnosti, zvláště u vzhledu
vysázených vzorců. Pokud si tedy chcete být jisti tím, jak něco vypadá,
sáhněte prosím po verzi v PDF.
Upozornění: Přesný vzhled vysázených konstrukcí je v PDF
verzi! Ve webové verzi mohou být různé nepřesnosti, zvláště u vzhledu
vysázených vzorců. Pokud si tedy chcete být jisti tím, jak něco vypadá,
sáhněte prosím po verzi v PDF.