Recepty z programátorské kuchařky
Vyhledávací stromy
Aktuální verze kuchařky: leden 2022
V kuchařce první série jsme probrali základní způsoby ukládání dat v počítači, tzv. datové struktury, a také často používané programátorské techniky. Konkrétně jsme se naučili udržovat čísla nebo jiné objekty v poli, ve spojovém seznamu, v grafu nebo ve stromu. Ukázali jsme si rekurzi a její využití v backtrackingu (prostém zkoušení všech možností). Dále jsme již nakoukli pod pokličku dalším technikám: rozděl a panuj, dynamickému programování, hladovým algoritmům a pár dalším.
Nyní se podíváme podrobněji na binární vyhledávání, které bylo rovněž minule představeno, a pokusíme se ho vylepšit, abychom mohli průběžně měnit data, v nichž vyhledáváme. Zdá-li se vám to na jednu kuchařku málo, vězte, že problém není jednoduchý, ale zajímavý a řešení jsou navíc v praxi často používána.
Nejprve však zopakujme binární vyhledávání.
Binární vyhledávání
Stejně jako minule máme obrovské pole setříděných záznamů, třeba identifikačních čísel studentů nejmenované univerzity (záznamy však nemusí být čísla, stačí, když jsou navzájem porovnatelné). Naším úkolem je najít záznam z v poli s N záznamy x1 < x2 < … < xN.Při použití binárního vyhledávání neboli půlení intervalu se podíváme na prostřední záznam xm a porovnáme s ním naše z. Pokud z<xm, víme, že se z nemůže vyskytovat „napravo“ od xm, protože tam jsou všechny záznamy větší než xm, a tím spíše než z. Analogicky pokud z>xm, nemůže se z vyskytovat v první polovině pole. V obou případech nám zbude jedna polovina a v ní budeme pokračovat stejným způsobem. Tak budeme postupně půlit interval, ve kterém se z může nacházet, až buďto z najdeme, nebo vyloučíme všechny prvky, kde by mohlo být.
Tento algoritmus můžeme naprogramovat buďto rekurzivně, nebo pomocí cyklu, v němž si budeme udržovat interval <l,r>, ve kterém se hledaný prvek ještě může nacházet. My si ukážeme přístup s cyklem:
def bin_najdi(z):
levy = 0
pravy = N
while levy <= pravy:
median = (levy+pravy)/2
# hledaná hodnota je vlevo
if z < x[median]:
pravy = median - 1
# je vpravo
elif z > x[median]:
levy = median+1
# našli jsme přímo hodnotu
else:
return median
# hledaná hodnota nebyla nikde
return -1
int bin_najdi(int z) {
int levy, pravy, median;
// interval, ve kterém hledáme
levy = 0; pravy = N;
// dokud interval ještě není prázdný
while (levy <= pravy) {
median = (levy+pravy)/2;
// hledaná hodnota je vlevo
if (z < x[median])
pravy = median-1;
// je vpravo
else if (z > x[median])
levy = median+1;
else // našli jsme ji
return median;
}
return -1; // hledaná hodnota nebyla nikde
}
Samozřejmě bychom při vyhledávání záznamu mohli být ještě chytřejší. Víme-li třeba, že čísla jsou z rozsahu 1 až 1000 a dostaneme číslo 900, můžeme se napřed podívat do devíti desetin pole místo do poloviny. Obecně se tedy snažíme odhadovat, kde bude záznam v rámci pole podle jeho hodnoty. Tomuto přístupu se říká interpolační vyhledávání a v průměru je lepší než binární (průměrná časová složitost je O(log log N)), byť v nejhorším případě je lineární.
Binární vyhledávání je velmi rychlé, pokud máme možnost si data předem setřídit. Jakmile ale potřebujeme za běhu programu přidávat a odebírat záznamy, se zlou se potážeme. Buďto budeme mít záznamy uložené v poli a pak nezbývá než při zatřiďování nového prvku ostatní „rozhrnout“, což může trvat až N kroků, anebo si je budeme udržovat v nějakém seznamu, do kterého dokážeme přidávat v konstantním čase, jenže pak pro změnu nebudeme při vyhledávání schopni najít tolik potřebnou polovinu.
Zkusme ale provést jednoduchý myšlenkový pokus:
Vyhledávací stromy
Představme si, jakými všemi možnými cestami se může v našem poli binární vyhledávání ubírat. Na začátku porovnáváme s prostředním prvkem a podle výsledku se vydáme jednou ze dvou možných cest (nebo rovnou zjistíme, že se jedná o hledaný prvek, ale to není moc zajímavý případ). Na každé cestě nás zase čeká porovnání se středem příslušného intervalu a to nás opět pošle jednou ze dvou dalších cest atd. To si můžeme přehledně popsat pomocí stromu:
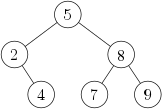
Jeden vrchol stromu prohlásíme za kořen a ten bude odpovídat celému poli (a jeho prostřednímu prvku). K němu budou připojené vrcholy obou polovin pole (opět obsahující příslušné prostřední prvky) a tak dále. Ovšem jakmile známe tento strom, můžeme náš půlící algoritmus provádět přímo podle stromu (ani k tomu nepotřebujeme vidět původní pole a umět v něm hledat poloviny): začneme v kořeni, porovnáme a podle výsledku se buďto přesuneme do levého, nebo pravého podstromu, a tak dále. Každý průběh algoritmu bude tedy odpovídat nějaké cestě z kořene stromu do hledaného vrcholu.
Teď si ale všimněte, že aby hledání hodnoty podle stromu fungovalo, strom vůbec nemusel vzniknout půlením intervalu – stačilo, aby v každém vrcholu platilo, že všechny hodnoty v levém podstromu jsou menší než tento vrchol a naopak hodnoty v pravém podstromu větší. Hledání v témže poli by také popisovaly následující stromy (např.):
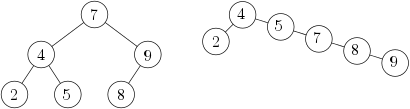
Hledací algoritmus podle jiných stromů samozřejmě už nemusí mít pěknou logaritmickou složitost (kdybychom hledali podle „degenerovaného“ stromu z pravého obrázku, trvalo by to dokonce lineárně). Důležité ale je, že takovéto stromy se dají poměrně snadno modifikovat a že je při troše šikovnosti můžeme udržet dostatečně podobné ideálnímu půlení intervalu. Pak bude hloubka stromu stále O(log N), tím pádem i časová složitost hledání, a jak za chvilku uvidíme, i mnohých dalších operací.
Definice
Zkusme si tedy pořádně nadefinovat to, co jsme právě vymysleli:
Binární vyhledávací strom (podomácku BVS) je buď prázdná množina, nebo kořen obsahující jednu hodnotu a mající dva podstromy (levý a pravý). Tyto podstromy jsou opět BVS, ovšem takové, že všechny hodnoty uložené v levém podstromu jsou menší než hodnota v kořeni, a ta je naopak menší než všechny hodnoty uložené v pravém podstromu.
Úmluva: Pokud x je kořen a Lx a Rx jeho levý a pravý podstrom, pak kořenům těchto podstromů (pokud nejsou prázdné) budeme říkat levý a pravý syn vrcholu x a naopak vrcholu x budeme říkat otec těchto synů. Pokud je některý z podstromů prázdný, pak vrchol x příslušného syna nemá. Vrcholu, který nemá žádné syny, budeme říkat list vyhledávacího stromu. Všimněte si, že pokud x má jen jediného syna, musíme stále rozlišovat, je-li to syn levý, nebo pravý, protože potřebujeme udržet správné uspořádání hodnot. Také si všimněte, že pokud známe syny každého vrcholu, můžeme již rekonstruovat všechny podstromy.
Každý BVS také můžeme popsat velmi jednoduchou strukturou v paměti:
class Vrchol:
self.levy = None
self.pravy = None
self.x = None
struct vrchol {
struct vrchol *levy, *pravy; // synové
int x; // hodnota ve vrcholu
};
Pokud některý ze synů neexistuje, zapíšeme do příslušné položky hodnotu NULL.
Hledání
V řeči BVS můžeme přeformulovat náš vyhledávací algoritmus takto:
# Dostane kořen stromu a hodnotu. Vrátí vrchol,
# ve kterém se hodnota nachází, nebo None, když
# ve stromu není.
def strom_najdi(vrchol, x):
while (v != None) and (vrchol.x != x):
if x < vrchol.x:
vrchol = vrchol.levy
else:
vrchol = vrchol.pravy
return vrchol
/* Dostane kořen stromu a hodnotu. Vrátí vrchol,
kde se nachází, nebo NULL, není-li. */
struct vrchol *strom_najdi(struct vrchol *v,
int x)
{
while (v != NULL && v->x != x) {
if (x < v->x)
v = v->levy;
else
v = v->pravy;
}
return v;
}
Funkce strom_najdi bude pracovat v čase O(h), kde h je hloubka stromu, protože
začíná v kořeni a v každém průchodu cyklem postoupí o jednu hladinu níže.
Vkládání
Co kdybychom chtěli do stromu vložit novou hodnotu (aniž bychom se teď starali
o to, zda tím strom nemůže degenerovat)? Stačí zkusit hodnotu najít, a pokud tam
ještě nebyla, určitě při hledání narazíme na odbočku, která je NULL. A přesně
na toto místo připojíme nově vytvořený vrchol, aby byl správně uspořádán
vzhledem k ostatním vrcholům (že tomu tak je, plyne z toho, že při hledání jsme
postupně vyloučili všechna ostatní místa, kde nová hodnota být nemohla).
Naprogramujeme opět snadno, tentokráte si ukážeme rekurzivní zacházení se stromy:
# Dostane kořen stromu a hodnotu ke vložení,
# vrátí nový kořen
def strom_vloz(vrchol, x):
# prázdný strom
if vrchol is None:
# založíme nový kořen
vrchol = Vrchol()
vrchol.levy = None
vrchol.pravy = None
vrchol.x = x
elif x < vrchol.x
# vkládáme vlevo
vrchol.levy = strom_vloz(vrchol.levy, x)
elif x > vrchol.x:
# vkládáme vpravo
vrchol.pravy = strom_vloz(vrchol.pravy, x)
return vrchol
/* Dostane kořen stromu a hodnotu ke vložení,
vrátí nový kořen. */
struct vrchol *strom_vloz(struct vrchol *v,
int x)
{
if (v == NULL) { // prázdný strom
// založíme nový kořen
v = malloc(sizeof(struct vrchol));
v->levy = v->pravy = NULL;
v->x = x;
} else if (x < v->x) // vkládáme vlevo
v->levy = strom_vloz(v->levy, x);
else if (x > v->x) // vkládáme vpravo
v->pravy = strom_vloz(v->pravy, x);
return v;
}
Mazání
Mazání bude o kousíček pracnější, musíme totiž rozlišit tři případy: Pokud je mazaný vrchol list, stačí ho vyměnit zaNULL. Pokud má právě jednoho syna, stačí náš vrchol v
ze stromu odstranit a syna přepojit k otci v. Ale pokud má syny dva, najdeme největší hodnotu
v levém podstromu (tu najdeme tak, že půjdeme jednou doleva a pak pořád doprava),
umístíme ji do stromu namísto mazaného vrcholu a v levém podstromu ji pak smažeme
(což už umíme, protože má 1 nebo 0 synů).
Program následuje:
def strom_vymaz(vrchol, x):
if vrchol is None:
# prázdný strom
return vrchol
elif x < vrchol.x:
# hledáme x
vrchol.levy = strom_vymaz(vrchol.levy, x)
elif x > vrchol.x:
vrchol.pravy = strom_vymaz(vrchol.pravy, x)
else:
# našli jsme x, jaké má syny?
if (vrchol.levy is None) and (vrchol.pravy is None):
return None
elif vrchol.levy is None:
# má jen pravého syna
return vrchol.pravy
elif vrchol.pravy is None:
# má jen levého syna
return vrchol.levy
else:
# má oba syny
w = vrchol.levy
while not w.pravy is None:
w = w.pravy
vrchol.x = w.x # prohazujeme
# mažeme původní max(L)
vrchol.levy=strom_vymaz(vrchol.levy, w.x)
return vrchol
/* Parametry stejně jako strom_vloz */
struct vrchol *strom_vymaz(struct vrchol *v,
int x)
{
struct vrchol *w, *ret = v;
if (v == NULL) return v; // prázdný strom
else if (x < v->x) // hledáme x
v->levy = strom_vymaz(v->levy, x);
else if (x > v->x)
v->pravy = strom_vymaz(v->pravy, x);
else { // našli jsme x ... jaké má syny?
if (v->levy == NULL
&& v->pravy == NULL) { // žádné
free(v);
return NULL;
} else if (v->levy == NULL) {
// jen pravý syn
ret = v->pravy;
free(v);
return ret;
} else if (v->pravy == NULL) {
// jen levý syn
ret = v->levy;
free(v);
return ret;
} else { // má oba dva syny
w = v->levy; // hledáme max(L)
while (w->pravy != NULL)
w = w->pravy;
v->x = w->x; // prohazujeme
// mažeme původní max(L)
v->levy = strom_vymaz(v->levy, w->x);
}
}
return v;
}
Když do stromu z našeho prvního obrázku zkusíme přidávat nebo z něj odebírat prvky, dopadne to takto:
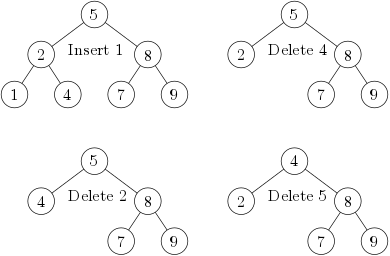
Jak vkládání, tak mazání opět budou trvat O(h), kde h je hloubka stromu. Ale pozor, jejich používáním může h nekontrolovatelně růst (v závislosti na počtu prvků ve stromu).
Cvičení
- Zkuste najít nějaký příklad, kdy h dosáhne až N – při postupném budování stromu operacemi vkládání i při mazání ze stromu hloubky O(log N).
Procházení stromu
Pokud bychom chtěli všechny hodnoty ve stromu vypsat, stačí strom rekurzivně projít a sama definice uspořádání hodnot ve stromu nám zajistí, že hodnoty vypíšeme ve vzestupném pořadí: nejdříve levý podstrom, pak kořen a pak podstrom pravý. Časová složitost je, jak se snadno nahlédne, lineární, protože strávíme konstantní čas vypisováním každého prvku a prvků je právě N. Program bude opět přímočarý:
def strom_ukaz(vrchol):
if vrchol is None:
return
print("({}){}({})".format(
strom_ukaz(vrchol.levy),
vrchol.x,
strom_ukaz(vrchol.pravy)
))
void strom_ukaz(struct vrchol *v){
if (v == NULL)
return; // není co dál dělat
printf("(");
strom_ukaz(v->levy);
printf(")\%d(",v->x);
strom_ukaz(v->pravy);
printf(")");
}
Vyvážené stromy
S binárními stromy lze dělat všelijaká kouzla a prakticky všechny stromové algoritmy mají společné to, že jejich časová složitost je lineární v hloubce stromu. (Pravda, právě ten poslední je výjimka, leč všechny prvky rychleji než lineárně s N opravdu nevypíšeme.)Jenže jak jsme viděli, neopatrným insertováním a deletováním prvků mohou snadno vznikat všelijaké degenerované stromy, které mají lineární hloubku. Abychom tomu zabránili, musíme stromy vyvažovat. To znamená definovat si nějaké šikovné omezení na tvar stromu, aby hloubka byla vždy O(log N). Možností je mnoho, my uvedeme jen ty nejdůležitější:
Dokonale vyvážený budeme říkat takovému stromu, ve kterém pro každý vrchol platí, že počet vrcholů v jeho levém a pravém podstromu se liší nejvýše o jedničku. Takové stromy kopírují dělení na poloviny při binárním vyhledávání, a proto mají vždy logaritmickou hloubku. Jediné, čím se liší, je, že mohou zaokrouhlovat na obě strany, zatímco náš půlící algoritmus zaokrouhloval polovinu vždy dolů, takže levý podstrom nemohl být nikdy větší než pravý.
Z toho také plyne, že se snadnou modifikací půlícího algoritmu dá dokonale vyvážený BVS v lineárním čase vytvořit ze setříděného pole. Bohužel se ale při Insertu a Deletu nedá v logaritmickém čase strom znovu vyvážit.
AVL stromy
Zkusíme tedy vyvažovací podmínku trochu uvolnit a vyžadovat, aby se u každého vrcholu lišily o jedničku nikoliv velikosti podstromů, nýbrž pouze jejich hloubky. Takovým stromům se říká AVL stromy a mohou vypadat třeba takto: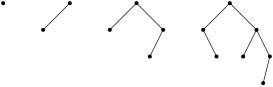
Každý dokonale vyvážený strom je také AVL stromem, ale jak je vidět na předchozím obrázku, opačně to platit nemusí. To, že hloubka AVL stromů je také logaritmická, proto není úplně zřejmé a zaslouží si to trochu dokazování:
Věta: AVL strom o N vrcholech má hloubku O(log N).
 Důkaz: Označme Ad nejmenší možný počet vrcholů, jaký může být
v AVL stromu hloubky d. Snadno zjistíme, že A1=1, A2=2,
A3=4 a A4=7 (příslušné minimální stromy najdete na předchozím obrázku).
Navíc platí, že Ad=1 + Ad-1 + Ad-2, protože každý minimální
strom hloubky d musí mít kořen a 2 podstromy, které budou opět minimální,
protože jinak bychom je mohli vyměnit za minimální a tím snížit počet vrcholů
celého stromu. Navíc alespoň jeden z podstromů musí mít hloubku d-1 (protože
jinak by hloubka celého stromu nebyla d) a druhý hloubku d-2 (podle
definice AVL stromu může mít d-1 nebo d-2, ale s menší hloubkou bude
mít evidentně méně vrcholů).
Důkaz: Označme Ad nejmenší možný počet vrcholů, jaký může být
v AVL stromu hloubky d. Snadno zjistíme, že A1=1, A2=2,
A3=4 a A4=7 (příslušné minimální stromy najdete na předchozím obrázku).
Navíc platí, že Ad=1 + Ad-1 + Ad-2, protože každý minimální
strom hloubky d musí mít kořen a 2 podstromy, které budou opět minimální,
protože jinak bychom je mohli vyměnit za minimální a tím snížit počet vrcholů
celého stromu. Navíc alespoň jeden z podstromů musí mít hloubku d-1 (protože
jinak by hloubka celého stromu nebyla d) a druhý hloubku d-2 (podle
definice AVL stromu může mít d-1 nebo d-2, ale s menší hloubkou bude
mít evidentně méně vrcholů).
Spočítat, kolik přesně je Ad, není úplně snadné. Nám však postačí dokázat, že Ad ≥ 2d/2. To provedeme indukcí: Pro d<4 to plyne z ručně spočítaných hodnot. Pro d≥ 4 je Ad = 1 + Ad-1 + Ad-2 > 2(d-1)/2 + 2(d-2)/2 = 2d/2 ·(2-1/2 + 2-1 ) > 2d / 2 (součet čísel v závorce je ≈ 1.207).
Jakmile už víme, že Ad roste s d alespoň exponenciálně, tedy že ∃c: Ad ≥ cd, důkaz je u konce: Máme-li AVL strom T na N vrcholech, najdeme si nejmenší d takové, že Ad ≤ N. Hloubka stromu T může být maximálně d, protože jinak by T musel mít alespoň Ad+1 vrcholů, ale to je více než N. A jelikož Ad rostou exponenciálně, je d ≤ logc N, čili d=O(log N). Q.E.D.
AVL stromy tedy vypadají nadějně, jen stále nevíme, jak provádět Insert a Delete tak, aby strom zůstal vyvážený. Nemůžeme si totiž dovolit strukturu stromu měnit libovolně – stále musíme dodržovat správné uspořádání hodnot. K tomu se nám bude hodit zavést si nějakou množinu operací, o kterých dokážeme, že jsou korektní, a pak strukturu stromu měnit vždy jen pomocí těchto operací. Budou to rotace a dvojrotace.
Rotace
Rotací binárního stromu (respektive nějakého podstromu) nazveme jeho „překořenění“ za některého ze synů kořene. Místo formální definice ukažme raději obrázek (trojúhelník zastupuje podstrom, který může být v některých případech i prázdný):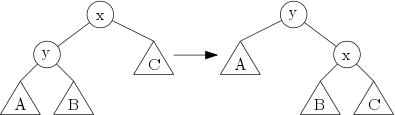
Strom jsme překořenili za vrchol y a přepojili jednotlivé podstromy tak, aby byly vzhledem k x a y opět uspořádané správně (všimněte si, že je jen jediný způsob, jak to udělat). Jelikož se tím okolí vrcholu y „otočilo“ po směru hodinových ručiček, říká se takové operaci rotace doprava. Inverzní operaci (tj. překořenění za pravého syna kořene) se říká rotace doleva a na našem obrázku odpovídá přechodu zprava doleva.
Dvojrotace
Také si nakreslíme, jak to dopadne, když provedeme dvě rotace nad sebou lišící se směrem (tj. jednu levou a jednu pravou nebo opačně). Tomu se říká dvojrotace a jejím výsledkem je překořenění podstromu za vnuka kořene připojeného „cikcak“. Raději opět předvedeme na obrázku: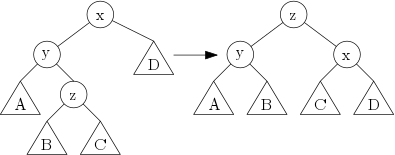
Znaménka
Při vyvažování se nám bude hodit pamatovat si u každého vrcholu, v jakém vztahu jsou hloubky jeho podstromů. Tomu budeme říkat znaménko vrcholu a bude buďto 0, jsou-li oba stejně hluboké, - pro levý podstrom hlubší, nebo + pro pravý hlubší. V textu budeme znaménka, respektive vrcholy se znaménky značit ⊙, ⊖ a ⊕.Pokud celý strom zrcadlově obrátíme (prohodíme levou a pravou stranu), znaménka se změní na opačná (⊕ a ⊖ se prohodí, ⊙ zůstane). Toho budeme často využívat a ze dvou zrcadlově symetrických situací popíšeme jenom jednu s tím, že druhá se v algoritmu zpracuje symetricky.
Často také budeme potřebovat nalézt otce nějakého vrcholu. To můžeme zařídit buďto tak, že si do záznamů popisujících vrcholy stromu přidáme ještě ukazatele na otce a budeme ho ve všech operacích poctivě aktualizovat, anebo využijeme toho, že jsme do daného vrcholu museli někudy přijít z kořene, a celou cestu z kořene si zapamatujeme v nějakém zásobníku a postupně se budeme vracet.
Tím jsme si připravili všechny potřebné ingredience, tož s chutí do toho.
Vyvažování po Insertu
Když provedeme Insert tak, jak jsme ho popisovali u obecných vyhledávacích stromů, přibyde nám ve stromu list. Pokud se tím AVL vyváženost neporušila, stačí pouze opravit znaménka na cestě z nového listu do kořene (všude jinde zůstala zachována). Pakliže porušila, musíme s tím něco provést, konkrétně ji šikovně zvolenými rotacemi opravit. Popíšeme algoritmus, který bude postupovat od listu ke kořeni a vše potřebné zařídí.
Nejprve přidání listu samotné:
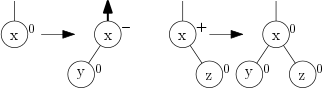
Pokud jsme přidali list (bez újmy na obecnosti levý, jinak vyřešíme zrcadlově) vrcholu se znaménkem ⊙, změníme znaménko na ⊖ a pošleme o patro výš informaci o tom, že hloubka podstromu se zvýšila (to budeme značit šipkou). Přidali-li jsme list k ⊕, změní se na ⊙ a hloubka podstromu se nemění, takže můžeme skončit.
Nyní rozebereme případy, které mohou nastat na vyšších hladinách, když nám z nějakého podstromu přijde šipka. Opět budeme předpokládat, že přišla zleva; pokud zprava, vyřešíme zrcadlově. Pokud přišla do ⊙ nebo ⊕, ošetříme to stejně jako při přidání listu:
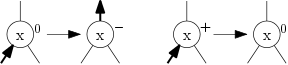
Pokud ale vrchol x má znaménko ⊖, nastanou potíže: levý podstrom má teď hloubku o 2 vyšší než pravý, takže musíme rotovat. Proto se podíváme o patro níž, jaké je znaménko vrcholu y pod šipkou, abychom věděli, jakou rotaci provést. Jedna možnost je tato (y je ⊖):
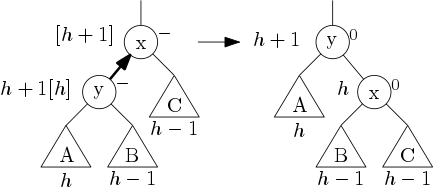
Tehdy provedeme jednoduchou rotaci vpravo. Jak to dopadne s hloubkami, jsme přikreslili do obrázku – pokud si hloubku podstromu A označíme jako h, B musí mít hloubku h-1, protože y je ⊖, atd. Jen nesmíme zapomenout, že v x jsme ještě ⊖ nepřepočítali (vede tam přeci šipka), takže ve skutečnosti je jeho levý podstrom o 2 hladiny hlubší než pravý (původní hloubky jsme na obrázku naznačili [v závorkách]). Po zrotování vyjdou u x i y znaménka ⊙ a celková hloubka se nezmění, takže jsme hotovi.
Další možnost je y jako ⊕:
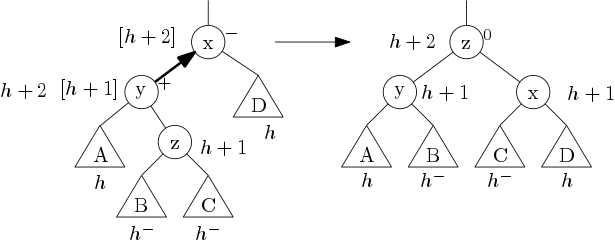
Tehdy se podíváme ještě o hladinu níž a provedeme dvojrotaci. (Nemůže se nám stát, že by z neexistovalo, protože jinak by v y nebylo ⊕.) Hloubky opět najdete na obrázku. Jelikož z může mít libovolné znaménko, jsou hloubky podstromů B a C buďto h, nebo h-1, což značíme h-. Podle toho pak vyjdou znaménka vrcholů x a y po rotaci. Každopádně vrchol z vždy obdrží ⊙ a celková hloubka se nemění, takže končíme.
Poslední možnost je, že by y byl ⊙, ale tu vyřešíme velmi snadno: všimneme si, že nemůže nastat. Kdykoliv totiž posíláme šipku nahoru, není pod ní ⊙. (Kontrolní otázka: jak to, že ⊕ může nastat?)
Vyvažování po Deletu
Vyvažování po Deletu je trochu obtížnější, ale také se dá popsat pár obrázky. Nejdříve opět rozebereme základní situace: odebíráme list (bez újmy na obecnosti (BÚNO) levý) nebo vnitřní vrchol s jediným synem (tehdy ale musí být jeho jediný syn listem, jinak by to nebyl AVL strom):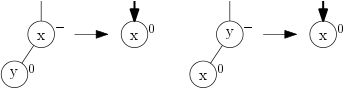
Šipkou dolů značíme, že o patro výš posíláme informaci o tom, že se hloubka podstromu snížila o 1. Pokud šipku dostane vrchol typu ⊖ nebo ⊙, vyřešíme to snadno:
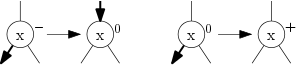
Problematické jsou tentokráte ty případy, kdy šipku dostane ⊕. Tehdy se musíme podívat na znaménko opačného syna a podle toho rotovat. První možnost je, že opačný syn má ⊕:
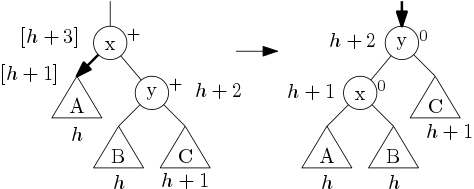
Tehdy provedeme rotaci vlevo, x i y získají nuly, ale celková hloubka stromu se sníží o hladinu, takže nezbývá, než poslat šipku o patro výš.
Pokud by y byl ⊙:
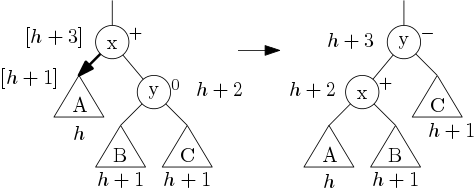
Opět rotace vlevo, ale tentokráte se zastavíme, protože celková hloubka se nezměnila.
Poslední, nejkomplikovanější možnost je, že by y byl ⊖:
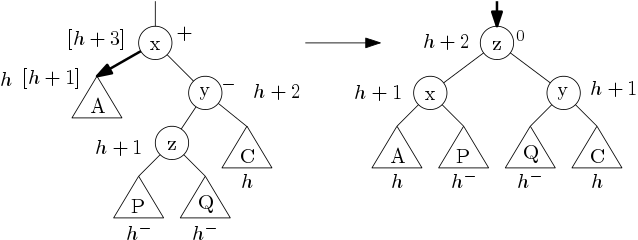
V tomto případě provedeme dvojrotaci (z určitě existuje, jelikož y je typu ⊖), vrcholy x a y obdrží znaménka v závislosti na původním znaménku vrcholu z a celý strom se snížil, takže pokračujeme o patro výš.
Happy end
Jak při Insertu, tak při Deletu se nám podařilo strom upravit tak, aby byl opět AVL stromem, a trvalo nám to lineárně s hloubkou stromu (konáme konstantní práci na každé hladině), čili stejně jako trvá Insert a Delete samotný. Jenže o AVL stromech jsme již dokázali, že mají hloubku vždy logaritmickou, takže jak hledání, tak Insert a Delete zvládneme v logaritmickém čase (vzhledem k aktuálnímu počtu prvků ve stromu).Další typy stromů
AVL stromy samozřejmě nejsou jediný způsob, jak zavést stromovou datovou strukturu s logaritmicky rychlými operacemi. Jaké jsou další?
2-3-stromy nemají v jednom vrcholu uloženu jednu hodnotu, nýbrž jednu nebo dvě (a synové jsou pak 2 nebo 3, odtud název). Přidáme navíc pravidlo, že všechny listy jsou na téže hladině. Hloubka vyjde logaritmická, vyvažování řešíme pomocí spojování a rozdělování vrcholů.
Červeno-černé stromy si místo znamének vrcholy barví. Každý je buďto červený nebo černý a platí, že nikdy nejsou dva červené vrcholy pod sebou a že na každé cestě z kořene do listu je stejný počet černých vrcholů. Hloubka je pak znovu logaritmická.
Po Insertu a Deletu barvy opravujeme rotováním a přebarvováním na cestě do kořene, jen je potřeba rozebrat podstatně více případů než u AVL stromů. (Za to jsme ale odměněni tím, že nikdy neděláme více než 2 rotace.) Počet případů k rozebrání lze omezit zpřísněním podmínek na umístění červených vrcholů – dvěma různým takovým zpřísněním se říká AA-stromy a left-leaning červeno-černé stromy.
Interpretujeme-li červené vrcholy jako rozšíření otcovského vrcholu o další hodnoty, pochopíme, že jsou červeno-černé stromy jen jiným způsobem záznamu 2-4-stromů. Proč se takový kryptický překlad dělá? S třemi potomky vrcholu a dvěma hodnotami se pracuje nešikovně.
V případě splay stromů nezavádíme žádnou vyvažovací podmínku, nýbrž definujeme, že kdykoliv pracujeme s nějakým vrcholem, vždy si jej vyrotujeme do kořene, a pokud to jde, preferujeme dvojrotace. Takové operaci se říká Splay a dají se pomocí ní definovat operace ostatní: Find hodnotu najde a poté na ni zavolá Splay. Insert si nechá vysplayovat předchůdce nové hodnoty a vloží nový vrchol mezi předchůdce a jeho pravého syna. Delete vysplayuje mazaný prvek, pak uvnitř pravého podstromu vysplayuje minimum, takže bude mít jen jednoho syna a můžeme jím tedy nahradit mazaný prvek v kořeni.
Jednotlivé operace samozřejmě mohou trvat až lineárně dlouho, ale dá se o nich dokázat, že jejich amortizovaná složitost je vždy O(log N). Tím chceme říci, že provést t po sobě jdoucích operací začínajících prázdným stromem trvá O(t· log N) (některé operace mohou být pomalejší, ale to je vykoupeno větší rychlostí jiných).
To u většiny použití stačí – datovou strukturu obvykle používáme uvnitř nějakého algoritmu a zajímá nás, jak dlouho běží všechny operace dohromady – a navíc je Splay stromy daleko snazší naprogramovat než nějaké vyvažované stromy. Mimo to mají Splay stromy i jiné krásné vlastnosti: přizpůsobují svůj tvar četnostem hledání, takže často hledané prvky jsou pak blíž ke kořeni, snadno se dají rozdělovat a spojovat, atd.
Treapy jsou randomizovaně vyvažované stromy: něco mezi stromem (tree) a haldou (heap). Každému prvku přiřadíme váhu, což je náhodné číslo z intervalu < 0,1 >. Strom pak udržujeme uspořádaný stromově podle hodnot a haldově podle vah (všimněte si, že tím je jeho tvar určen jednoznačně, pokud tedy jsou všechny váhy navzájem různé, což skoro jistě jsou). Insert a Delete opravují haldové uspořádání velmi jednoduše pomocí rotací. Časová složitost v průměrném případě je O(log N).
BB-α stromy nabízí zobecnění dokonalé vyváženosti jiným směrem: zvolíme si vhodné číslo α a vyžadujeme, aby se velikost podstromů každého vrcholu lišila maximálně α-krát (prázdné podstromy nějak ošetříme, abychom nedělili nulou; dokonalá vyváženost odpovídá α=1 (až na zaokrouhlování)). V každém vrcholu si budeme pamatovat, kolik vrcholů obsahuje podstrom, jehož je kořenem, a po Insertu a Deletu přepočítáme tyto hodnoty na cestě zpět do kořene a zkontrolujeme, jestli je strom ještě stále α-vyvážený.
Pokud ne, najdeme nejvyšší místo, ve kterém se velikosti podstromů příliš liší, a vše od tohoto místa dolů znovu vytvoříme algoritmem na výrobu dokonale vyvážených stromů. Ten, pravda, běží v lineárním čase, ale čím větší podstrom přebudováváme, tím to děláme méně často, takže vyjde opět amortizovaně O(log N) na operaci.
Cvičení
- Jak konstruovat dokonale vyvážené stromy?
- Jak pomocí toho naprogramovat BB-α stromy?
- Najděte algoritmus, který k prvku v obecném vyhledávacím stromu najde jeho následníka, což je prvek s nejbližší vyšší hodnotou (zde předpokládejte, že ke každému prvku máte uložený ukazatel na jeho otce).
- Jak vypsat celý strom tak, že začnete v minimu a budete postupně hledat následníky? (I když nalezení následníka může trvat až O(h), všimněte si, že projití celého stromu přes následníky bude lineární.)
- Jak do vrcholů stromu ukládat různé pomocné informace, jako třeba počet vrcholů v podstromu každého vrcholu, a jak tyto informace při operacích se stromem (při Insertu, Deletu, rotaci) udržovat?
- Ukažte, že lze libovolný interval <a,b> rozložit na logaritmicky mnoho intervalů odpovídajících podstromům vyváženého stromu.
- Ukažte, že zkombinováním předchozích dvou cvičení lze odpovídat i na otázky typu „kolik si strom pamatuje hodnot ze zadaného intervalu“ v logaritmickém čase …
Poznámky
- Představte si, že budujete binární vyhledávací strom pomocí vkládání prvků v náhodném pořadí. Obecně nemusí být vyvážený, ale v průměru v něm bude možné vyhledávat v čase O(log N). Žádný div: Stromy, které nám vzniknou, odpovídají přesně možným průběhům QuickSortu, který má průměrnou časovou složitost O(N log N).
- Pokud bychom připustili, že se mohou vyskytnout dva stejné záznamy, budou stromy stále fungovat, jen si musíme dát o něco větší pozor na to, co všechno při operacích se stromem může nastat.
- Jakpak přišly AVL stromy ke svému jménu? Podle Adeľsona-Veľského a Landise, kteří je vynalezli.
- Rekurenci Ad=1 + Ad-1 + Ad-2, A1=1, A2=2 pro velikosti minimálních AVL stromů je samozřejmě možné vyřešit i přesně. Žádné překvapení se nekoná, objeví se totiž stará známá Fibonacciho čísla: An=Fn+2-1.