První série sedmnáctého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 17-1-1: Výdělek bratří Součků
- 17-1-2: Bůhdhova odměna
- 17-1-3: Chmatákův lup
- 17-1-4: Paloučkova výhra
- 17-1-5: Jazykozpytcův poklad
17-1-1 Výdělek bratří Součků (Zadání)
Řešení této úlohy by se dala rozdělit do tří skupin. Lineární, kvadratické (vůči délce vstupu) a nefunkční. Kromě toho několik lidí předpokládalo, že řetězce mohou být vůči sobě posunuté. Nechápu proč. Bratři byli vyslání na koncert společně a začali zapisovat oba hned na začátku.
No a jak mělo řešení vypadat? Nejprve je třeba si uvědomit, že pokud mají být řetězce záznamem toho samého, pak musí obsahovat stejný podřetězec, jehož opakováním vytvoříme Ainův i Kábelův záznam. No a jak dlouhý tento podřetězec může být? Jelikož jeho několikanásobným zopakováním musíme dostat jak Ainův, tak Kábelův záznam, musí jeho délka být největší společný dělitel délek záznamů Aina a Kábela, resp. NSD musí být jeho celočíselným násobkem.
Pokud bude tedy Ainův i Kábelův záznam složen z opakujícího se podřetězce délky NSD a tyto podřetězce budou u Aina i Kábela stejné, víme, že zápisy budou stejné. A pokud podmínka splněná nebude, zaznamenali oba něco jiného.
Algoritmus řešící úlohu je jenom přímočarou implementací popsaného postupu, jeho časová i paměťová složitost je lineární vůči délce zápisů obou bratří.
 Toto mělo být řešení této úlohy, ale při pročítání řešení účastníků jsem nalezl jedno výrazně elegantnější:
Toto mělo být řešení této úlohy, ale při pročítání řešení účastníků jsem nalezl jedno výrazně elegantnější:
var Ain,Kabel:string;
begin
write('Ain:');readln(Ain);
write('Kabel:');readln(Kabel);
if (Ain+Kabel = Kabel+Ain) then
writeln('Záznamy jsou stejné.')
else
writeln('Záznamy jsou ruzné.');
end.
A proč toto funguje? BÚNO (bez újmy na obecnosti) předpokládejme, že Kábelův záznam (označme jej K a jeho délku LK) je delší než Ainův (A, LA). Záznamy budeme indexovat od nuly. Zřejmě ono porovnání vypadá takto:
Z porovnání těchto řádků dostaneme jednoduše:
| K[i] | = K[i mod LA] | (1) |
| A[i] | = K[i] | (2) |
| A[i] | = K[LK-LA+i] | (3) |
Zkombinováním (1) a (3):
A po uvažování (2):
Iterováním této rovnosti pro libovolné celé c:
Z toho je již vidět (po chvilce zamyšlení), že:
a tedy rovnost je splněna, právě když jsou záznamy stejné.
17-1-2 Bůhdhova odměna (Zadání)
V této úloze nám nejde o nic jiného než o tak řečené barvení grafu, čili o přiřazení nějakých čísel (barev) 1, …, k vrcholům grafu tak, aby žádné dva vrcholy spojené hranou nedostaly stejnou barvu. Zjistit, jestli je graf nějakými k barvami obarvitelný, je obecně velice těžký problém (pro obecné grafy a k>2 ho nikdo neumí vyřešit v polynomiálním čase; případy k=1 a k=2 si rozmyslete sami, ty jsou pro změnu triviální). Ale my o našem grafu naštěstí víme, že je rovinný (viz povídání v tomto vydání naši kuchařky), což situaci značně mění.
Každý rovinný graf lze obarvit čtyřmi barvami (to ale vůbec není triviální dokázat, matematikové se s tím trápili více než 100 let a nejkratší známý důkaz má přes sto stránek a rozebírá 633 různých případů). My si dokážeme, že vždy stačí 6 barev a že Bůhdha má tedy vždy šanci svou odměnu rozdělit:
Věta: (o šesti barvách) Každý rovinný graf je možno obarvit šesti barvami.
Důkaz: Indukcí podle počtu vrcholů. Pokud má graf nejvýše 6 vrcholů, obarvit ho dozajista můžeme. Pokud je graf větší, věta dokázaná v kuchařce nám říká, že v něm vždy existuje nějaký vrchol v stupně maximálně 5. Když takový vrchol odstraníme, dostaneme menší graf a ten je již podle indukčního předpokladu obarvitelný. Následně do obarveného grafu vrchol v vrátíme, a jelikož má nejvýše 5 sousedů, vždy je pro v alespoň jedna barva volná.
Již tento důkaz nám dává jednoduchý algoritmus pro Bůhdhův problém, ale ještě si musíme rozmyslet, jak neztrácet příliš mnoho času hledáním vrcholů nízkého stupně. Předem si spočítáme stupně všech vrcholů a do fronty uložíme ty vrcholy, které měly už na počátku stupeň ≤ 5. Poté postupně čteme vrcholy z fronty, snižujeme stupně jejich sousedům a jakmile některému sousedovi klesne stupeň pod 6, přidáme jej na konec fronty. Tím jsme vlastně sestrojili takové uspořádání vrcholů, že z každého vrcholu vede „doprava“ nejvýše 5 hran. Stačí tedy frontu projít pozpátku a postupně přidělovat volné barvy.
Tento algoritmus má lineární časovou i prostorovou složitost O(N) (všimněte si, že jelikož je graf rovinný, má O(N) hran). V programu stojí za zmínku snad jedině způsob reprezentace grafu: hrany máme uloženy v poli (každou dvakrát – v obou směrech), každý vrchol si pamatuje číslo první hrany z něj vycházející a každá hrana číslo následující hrany vycházející z téhož vrcholu. Při odtrhávání vrcholů hrany neodstraňujeme, pouze snižujeme stupně.
[P.S.: Po chvíli přemýšlení můžete náš důkaz upravit tak, aby ukazoval, že stačí 5 barev. Bůhdha se ale spokojí s šesti, takže mu nebudeme komplikovat život.]
Na závěr ještě ukážeme několik variant hladového barvícího algoritmu, který se často objevoval ve vašich řešeních a bohužel pro rovinné grafy nemůže fungovat.
Hladové barvení funguje takto: probíráme vrcholy jeden po druhém a každému přidělíme nejnižší barvu, která není použitá již obarvenými sousedy tohoto vrcholu. Zkusme si rozmyslet, jak obarví následující grafy:
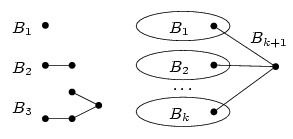
Zde B1 je graf z jednoho vrcholu a Bk+1 zkonstruujeme tak, že vezmeme B1, …, Bk a přidáme nový koncový vrchol vk spojený s koncovými vrcholy všech Bi hranou. Vrcholy nového grafu uspořádáme tak, že nejdříve půjdou vrcholy grafů B1, pak B2, …, Bk a na konec umístíme nově vytvořený vrchol.
Všimneme si, že zadáme-li hladovému barvícímu algoritmu graf Bk, spotřebuje k barev a vrchol vk obarví barvou k. I tentokrát nám k důkazu pomůže indukce: B1 obarvíme jednou barvou, B2 dvěma; pokud spustíme algoritmus na graf Bk, nejdříve obarví B1 až Bk-1, a jelikož jsou v tom správném pořadí a nevedou mezi nimi žádné hrany, dopadne to stejně, jako bychom barvili každý zvlášť, čili podle indukčního předpokladu budou jejich koncové vrcholy obarveny barvami 1 až k-1, proto na zbývající vrchol vk zbude barva k.
Jenže Bk je určitě rovinný graf, takže se dá obarvit šesti barvami (on je to dokonce strom, a tak stačí barvy dvě). Proto na něm pro k>6 nemůže hladový barvící algoritmus fungovat.
 Hladové barvení se ještě můžeme pokusit zachránit tím, že si zvolíme nějaké
šikovné pořadí vrcholů (konec konců i náš správný barvící algoritmus je vlastně
toho druhu). Ale jen tak ledajaké pořadí neposlouží:
Hladové barvení se ještě můžeme pokusit zachránit tím, že si zvolíme nějaké
šikovné pořadí vrcholů (konec konců i náš správný barvící algoritmus je vlastně
toho druhu). Ale jen tak ledajaké pořadí neposlouží:
- Pořadí podle rostoucích stupňů: v našem grafu pouze zparalelizuje barvení podgrafů B1, …, Bk – jenže mezi nimi nevedou žádné hrany, takže výsledek musí vyjít stejný.
- Podle klesajících stupňů: stačí k vrcholům přivěsit spoustu listů (vrcholů stupně 1) a tím algoritmus donutit k takovému pořadí, jaké chceme (možná bude potřebovat ještě jednu barvu na listy, ale tím hůř pro něj).
- Podle prohledávání do šířky: přidáme každému Bi ještě počáteční vrchol wi a při vytváření Bk+1 připojíme nový počáteční vrchol wk+1 k počátečním vrcholům w1, …, wk cestami délek zvolených tak, aby koncové vrcholy všech Bi byly ve stejné vzdálenosti od wk+1. Tehdy bude nový koncový vrchol vk+1 obarven až po všech ostatních vrcholech, čehož jsme přesně potřebovali dosáhnout. Graf přitom zůstane rovinný.
- Podle prohledávání do hloubky: tentokrát budeme přidávat hrany z vi do wi+1 a zařadíme je tak, aby je prohledávací algoritmus objevil vždy před hranou do vk+1. Takové cesty donutí prohledávání zpracovat nejdřív B1 až Bk a teprve pak barvit vrchol vk+1. Přitom vrchol wi má blokovánu pouze barvu i-1, takže ho určitě obarvíme jedničkou. Protipříklad opět zachráněn, graf opět zůstane rovinný. (Jediný problém je s hranou v1w2, na tu musíme přidat ještě jeden vrchol, jinak bude w2 obarven barvou 2, což nechceme.)
17-1-3 Chmatákův lup (Zadání)
Při řešení tohoto příkladu se mnoho z Vás inspirovalo příkladem v kuchařce. Avšak asi jenom polovina řešení byla správně. Hlavním problémem nefunkčních řešení bylo zejména nesprávné ošetření vícenásobného započtení jednoho předmětu.
Klíčové pozorování, které vede k pěknému řešení: Máme-li maximální dosažitelné ceny lupu pro všechny celočíselné kapacity batohu pomocí prvních k předmětů, snadno spočtěme maximální ceny pro prvních k+1 předmětů. A to tak, že zkusíme přidat k+1-ní předmět do batohu s k předměty a kapacitou nižší o hmotnost tohoto předmětu. Předmět nepřidáme, pokud cena takového lupu není vyšší od ceny lupu z prvních k předmětů v batohu se stejnou kapacitou. První předmět je možné vložit do batohu s kapacitou rovnou alespoň hmotnosti předmětu a cena lupu je maximální možná. Pro další předměty to plyne z indukce.
Budeme postupně zaplňovat tabulku podle popisu v pozorování. Z této tabulky snadno zrekonstruujeme vložené předměty. Stačí si uvědomit, že předmět i byl použit, pokud vylepšil cenu lupu v batohu se stejnou nosností bez tohoto předmětu.
Časová i paměťová složitost je O(P·N).
17-1-4 Paloučkova výhra (Zadání)
V této úloze jde o nalezení nejkratší kružnice v ohodnoceném grafu. Celkem často se vyskytovalo jedno popsaných řešení, ale našla se i originální řešení v O(N4), O(N5).
Jednodušší řešení je dynamické, upravím vlastně Floyd-Warshalla tak, že postupně rozšiřuji množinu S už prozkoumaných vrcholů. Na začátku do ní vložím libovolné 2 vrcholy a do matice vzdáleností D si uložím délky hran nebo příp. nekonečna (jako v kuchařce). Potom vždy vezmu vrchol k, který ještě není v S, a pro všechny jeho sousedy i,j, kteří už jsou v S (jsou-li takoví), prozkoumám cestu i...j. Pokud ji totiž už znám, určitě nevede přes k a k-i...j-k je tedy kružnice. Ze všech takto postupně nacházených kružnic si vyberu nejmenší a tu si zapíšu (pamatuji si vždy jen tu nejlepší) – to udělám tak, že si (stejně jako v kuchařce) pamatuji město s největším číslem na každé cestě E[i,j], updatuji ho při změně cesty, vypisuji rekurzí. Nemůžu nejmenší kružnici nijak přeskočit, protože jakmile právě přidávám do S její poslední vrchol, potom i a j se jednou trefí do jejich hran a pokud by její součástí měla být delší cesta než mnou nalezená i...j, nebyl by výsledek nejmenší kružnice. Už zbývá jen projet všechna i,j∈S a zjistit, zda nejsou i...k...j nebo i...j-k kratší než původní i...j nebo i...k a případně je vylepšit. Časová složitost jednodušší verze je O(N3), paměťová složitost O(N2).
 Další možnost řešení byla vybrat postupně každý vrchol jako
start a spustit z něj Dijkstrův algoritmus (kterým najdu nejkratší
cesty do všech ostatních vrcholů) a potom pro každou hranu nevedoucí
z/do startu prozkoumat nejkratší cesty vedoucí z jejich konců na
start. Pokud ani jedna z těchto cest není podmnožinou té druhé (na to
se stačí podívat na jejich první hrany, jestli některá není ta
prozkoumávaná), určitě tvoří buď kružnici nebo pseudokružnici
(s „ocáskem“). Tak jako tak si z těchto všech mohu zapamatovat nejkratší
(pseudo)kružnici, protože platí, že stejně musím (pro nějaký jiný
start) objevit i kružnici bez toho ocásku, a ta bude určitě kratší.
Časová složitost je zde (podle implementace Dijkstrova algoritmu)
O(N3) při nejjednodušší implementaci, O(MN log N) při použití
haldy a O(MN+N2 log N) při použití Fibonnacciho haldy. Rozdíl těchto
časových složitostí není sice velký (ty jsou v nejhorším vždy O(N3) až O(N3 log N)),
ale některé z těchto implementací jsou mnohem lepší pro řídké grafy.
Paměťová složitost je O(N2).
Další možnost řešení byla vybrat postupně každý vrchol jako
start a spustit z něj Dijkstrův algoritmus (kterým najdu nejkratší
cesty do všech ostatních vrcholů) a potom pro každou hranu nevedoucí
z/do startu prozkoumat nejkratší cesty vedoucí z jejich konců na
start. Pokud ani jedna z těchto cest není podmnožinou té druhé (na to
se stačí podívat na jejich první hrany, jestli některá není ta
prozkoumávaná), určitě tvoří buď kružnici nebo pseudokružnici
(s „ocáskem“). Tak jako tak si z těchto všech mohu zapamatovat nejkratší
(pseudo)kružnici, protože platí, že stejně musím (pro nějaký jiný
start) objevit i kružnici bez toho ocásku, a ta bude určitě kratší.
Časová složitost je zde (podle implementace Dijkstrova algoritmu)
O(N3) při nejjednodušší implementaci, O(MN log N) při použití
haldy a O(MN+N2 log N) při použití Fibonnacciho haldy. Rozdíl těchto
časových složitostí není sice velký (ty jsou v nejhorším vždy O(N3) až O(N3 log N)),
ale některé z těchto implementací jsou mnohem lepší pro řídké grafy.
Paměťová složitost je O(N2).
17-1-5 Jazykozpytcův poklad (Zadání)
Obě zadané úlohy patřily spíše k těm snazším a řešitelé, kteří úlohy odeslali, byli převážně dvou druhů. První, malá skupina těch, kteří si nejspíše pořádně nepřečetli zadání, řešila povětšinou něco úplně jiného. Skupina druhá, naštěstí podstatně větší, která se prokousala povídáním o jazycích a správně pochopila definici konečného automatu a gramatiky, po přečtení zadání bez problémů obě úlohy vyřešila.
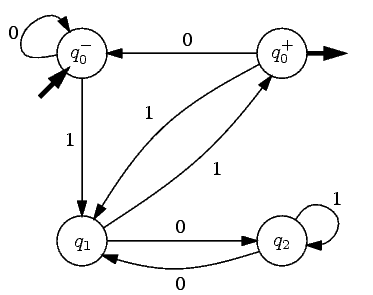
Jak tedy na konstrukci konečného automatu, který rozpoznává binární čísla dělitelná třemi a nedělitelná dvěma? Použijeme velice jednoduchý trik. Budeme automatem postupně cifru po cifře načítat číslo a průběžně si budeme pamatovat nikoli jeho hodnotu, nýbrž pouze zbytek po dělení šesti. Zjevně nám potom budou vyhovovat pouze čísla tvaru 6k+3 pro nějaké k, ostatní jsou buďto dělitelná dvojkou nebo nedělitelná trojkou. Když máme načtené číslo s aktuálním zbytkem z (tedy tvaru 6k+z), po načtení 0 dostaneme číslo 2(6k+z), po načtení 1 číslo 2(6k+z)+1. Zbývá si tedy pouze spočítat, jak se pro každé z a načtenou cifru zbytek změní.
Náš stroj tedy bude používat stavy Q={q0,…,q5}, kde stav qi značí, že aktuální zbytek je i. Počáteční stav bude q0 a jediný přijímací stav bude F={q3}. Přechodová funkce δ bude vypadat takto:
| δ | 0 | 1 |
| q0 | q0 | q1 |
| q1 | q2 | q3 |
| q2 | q4 | q5 |
| q3 | q0 | q1 |
| q4 | q2 | q3 |
| q5 | q4 | q5 |
Každý sám už si asi domyslí, že podobný postup by fungoval, pokud bychom měli zadanou libovolnou konečnou množinu M čísel, které musí, resp. nesmí dělit vstup. Stačí vzít tolik stavů, kolik je nejmenší společný násobek čísel z M, přepočítávat při načítání zbytek a vhodně zvolit přijímací stavy.
| - |
| 0 |
| + |
| 0 |
| + |
| 0 |
Když už máme hotový automat (Q,A,δ,q0,F), je, jak si také většina řešitelů správně všimla, velmi jednoduché podle něj zkonstruovat ekvivalentní gramatiku (VN,VT,S,P). Pro stavy automatu Q={q0,…,qk}, zavedeme do gramatiky neterminální symboly VN={Q0,…,Qk}, terminální symboly VT=A budou písmena abecedy, počáteční symbol S=Q0 bude neterminál odpovídající počátečnímu stavu automatu.
Pro každý stav qi a každé písmeno p se podíváme, jaký nový stav qj=δ(qi,p) vrací přechodová funkce. Do množiny přepisovacích pravidel P potom dáme příslušné pravidlo Qi→p Qj. Pokud je navíc stav qj přijímací, přidáme ještě pravidlo Qi→p. Každá expanze gramatiky zjevně následuje výpočet automatu, a tudíž generuje stejný jazyk.
| - |
| 0 |
| - |
| 0 |
| + |
| 0 |
Q
| → | 0Q
| ||||
Q
| → | 0Q
| ||||
| Q1 | → | 0Q2 | 1Q
| ||||
| Q2 | → | 0Q1 | 1Q2 |
První dva řádky jsou víceméně stejné, lze je tedy dokonce nahradit jediným řádkem Q0→0Q0 | 1Q1, příslušně modifikovat pravidlo pro Q1 a ušetřit tak jeden neterminální symbol.
V zadání jsme tvrdili, že regulárním jazykům odpovídají právě gramatiky s pravidly tvaru N→uM a N→u, kde N,M jsou neterminály a u je terminál. První část tohoto tvrzení, konstrukce ekvivalentní gramatiky ze zadaného automatu, jsme právě ukázali. Zbývá popsat konstrukci ekvivalentního automatu ze zadané gramatiky výše uvedeného tvaru. Ta se provede opačným postupem než při převodu automat → gramatika a detaily si jistě rozmyslí každý sám.