Čtvrtá série dvacátého druhého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 22-4-1: Zaheslované stránky
- 22-4-2: Rozvoz zásilek
- 22-4-3: Muzeum
- 22-4-4: Ořez zárodků
- 22-4-5: Energetické články
- 22-4-6: Umisťování panelů
- 22-4-7: Pozdrav z pravěku
22-4-1 Zaheslované stránky (Zadání)
Ano, je to úloha na grafy, dokonce orientované! Vrcholy jsou stránky, hrany si nastavíme, aby vedly z odemknutelného dokumentu na dokument s příslušným heslem. Potom má graf tu zvláštní vlastnost, že počet hran, které vychází z libovolného vrcholu, je roven 0, nebo 1.
To se bude jednak příjemně implementovat, druhak to silně omezuje strukturu takových grafů. Ptejme se na počet hran u každé komponenty slabé souvislosti (to je taková, která nehledí na orientaci hran) v závislosti na počtu vrcholů komponenty (n).
- Nejméně to může být n-1: v případě, že jde o strom. Odebrání libovolné hrany způsobí rozpad komponenty.
- Nejvíce to může být n, protože každému vrcholu přísluší nejvýše jeden výstupní konec hrany. Taková komponenta může být tvořena orientovanou kružnicí, vlastnost ale neporušíme ani tím, přilepíme-li k takové kružnici cestu vedoucí do nějakého jejího vrcholu. Situace dokonce může vypadat jako na obrázku:
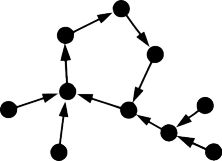
V obou případech stačí prolomit jedinou stránku. Našemu algoritmu proto stačí spočítat komponenty slabé souvislosti daného orientovaného grafu a určitě bychom to mohli v lineárním čase a prostoru stihnout spočítat tak, že bychom si situaci odorientovali a spouštěli do nových a nových vrcholů průchody do hloubky / šířky.
Můžeme to ale udělat jednodušeji. Uložíme-li graf do pole délky n, kde na i-tém místě uložíme, do kolikátého vrcholu míří hrana vycházející z i-tého vrcholu (nulu, pokud žádná nevychází), máme k dispozici šikovnou reprezentaci, kterou se snadno projdeme bez použití front a zásobníků: stačí si prstem (proměnnou) ukazovat, kde právě jsme, a jít „rovnou za nosem“.
Začneme-li si ukazovat v libovolném vrcholu komponenty prvního druhu, dostaneme se do kořene stromu, v komponentě druhého druhu se zacyklíme v jejím cyklu. Pokud se nám tyto případy podaří detekovat a zaznamenat do kořene / celé kružnice, že už jsme tam byli, můžeme při takové příležitosti přičíst k počtu nutně prolomených stránek jedničku.
Toto poznamenávání může probíhat ve zvláštním poli, kde si budeme při průchodu přepisovat tři značky: prolomeno, právě lámáno a netknuto. Na počátku je všude poznamenáno netknuto, při procházení za sebou pokládáme právě lámáno, což po dokončení průchodu zaměníme za prolomeno. Cyklus pak snadno detekujeme tím, že narazíme na značku právě lámáno, dojdeme-li někdy do situace prolomeno, můžeme skončit bez navýšení počtu nutných prolomení.
Ještě jednoduší je přepisovat uložený graf. Pěknou implementaci na tomto základě napsal Dominik Smrž – autorský program využívá jeho nápadu se zápornými čísly vrcholů coby identifikátory průchodů. Určitě si ho projděte, je krátký.
22-4-2 Rozvoz zásilek (Zadání)
Nejprve pár slov o tom, jak úlohu neřešit. Ne vždy je dobrý nápad zkontrolovat
úsek, kterým prochází největší počet dosud nezkontrolovaného zboží – mohlo
by se to totiž v budoucnu vymstít. Ukažme si to na protipříkladu (ve formátu
zadání úlohy): 1:1->2, 2:1->4, 2:3->6, 1:5->6 se dvěma skenery k dispozici.
V prvním kroku je sice nejvýnosnější zkontrolovat úsek 3-4,
ale tím dostanu řešení o nejvýše 5 zkontrolovaných kusech, zatímco
optimální řešení kontrolující úseky 1-2 a 5-6 dodá luxusních 6. Aneb
důkazy nejsou pro blaho opravovatelů, ale pro to, abyste si mohli být jisti
funkčností Vašich řešení.
Když tedy na první pohled nevíme, které řešení je nejlepší, zkusíme preventivně
všechny. A jak říká známe přísloví známé už z dob počítání na prstech, „od
backtracku k dynamice krůček.“ Budeme si tedy počítat, kolik nejvýše zásilek
zvládneme zkontrolovat pomocí k skenerů na stanicích 1..i, a to
v (dvourozměrném) poli soucet; pak optimální řešení úlohy zkontroluje právě
soucet[N][S] kusů zboží.
Jak spočísti hodnotu soucet[i][j]? Inu, pro i=1, tedy jeden skener,
je otázka jednoduchá, prohlédneme všechny stanice v intervalu 1..j a
podíváme se, ve které užitím skeneru zkontrolujeme nejvíce zboží – přesně to je
hodnota soucet[1][j]. Pro více skenerů už to ale takto jednoduše nejde,
viz první odstavec. Každopádně si můžeme říci – buďto oskenujeme úsek j-1:j (poslední úsek intervalu), nebo ne; spočítáme nejlepší řešení pro obě
situace a pamatujeme si jen to lepší. V druhém případě vlastně skenujeme jen na
intervalech 1..j-1, tedy počet kusů je soucet[i][j-1]. Prvý případ
je drobet složitější, na počtu zboží, které
oskenujeme v j-té stanici, se totiž promítne, jaké předchozí stanice jsme
již oskenovali. Každopádně to opět můžeme vzít hrubou silou, tedy postupně
uvážit, že před j-tou stanicí jsme jako poslední oskenovali k-tou pro
všechna k menší než j, a z těchto si vzít nejlepší řešení.
Nechť cena[k][j] říká, kolik zboží se proskenuje úsekem j-1:j,
byl-li nejlevější proskenovaný úsek k-1:k; pak by předchozí myšlenka
vypadala v pseudokódu následovně:
l = 0;
for(k=0;k<j;k++)
l = max(l,soucet[i-1][k] + cena[k][j]);
soucet[i][j] = max(soucet[i-1][j],l);
Bystrý čtenář si jistě klade otázku, jak víme, že v optimálním řešení pro i-1 skenerů na stanicích 1..k bude poslední skener právě na pozici k-1:k, to jest, že můžeme počítat cena[k][j] a ne nějakou nižší. Inu, my
to nevíme, ale je nám to jedno. Ono se bude stávat, že skener nebude na poslední
pozici a my tak vlastně v tomto kroku dostaneme horší řešení; jenže z nějakého
předchozího kroku už máme lepší.
Zbývá vysvětlit, jak efektivně spočteme cena[i][j]. Dělat to v průběhu počítání
není ono, protože spoustu věcí bychom dělali mockrát. Raději si hodnoty
spočítáme dopředu, všechny najednou.
Nejprve si intervaly dopravy zboží setřídíme vzestupně dle jejich koncových
zastávek. Pak postupně pro všechny úseky j-1:j provedeme následující: do
fronty si naházíme všechny intervaly dopravy zboží, které procházejí přes j-1:j, a při tom si
spočteme celkový počet zboží m v těchto intervalech. Pak budeme postupně brát
úseky i-1:i > j-1:j a spočteme cena[j][i]. Z fronty vyházíme ty intervaly,
které už do i-1:i nezasáhnou (takové se nacházejí jen a pouze na začátku
fronty), a o počet zboží v nich snížíme m, cena[j][i] je pak celková
suma zboží v intervalech procházejících přes i-1:i minus m. Pro
podrobnosti viz zdrojový kód.
Jak se přesvědčit, že algoritmus je správně? Inu, indukcí podle počtu skenerů a
zastávek. Pro jeden skener a libovolně zastávek náš algoritmus určitě funguje.
Udělejme tedy indukční krok pro N skenerů a S zastávek, za
předpokladu, že pro menší počet skenerů a zastávek algoritmus funguje. Pokud
optimální řešení neskenovalo poslední zastávku, tak tak neučiní ani náš
algoritmus, neboť si všimne, že soucet[N][S-1] je větší než libovolné
řešení skenující poslední zastávku (z indukčního předpokladu), a vítězíme. Pokud
optimální řešení poslední
zastávku skenovalo, podíváme se, jakou zastávku skenovalo jako předposlední,
nechť je to k-tá. Pak ono optimální řešení zkontroluje nejvýše soucet[N-1][k] + cena[k][j] zásilek (z indukčního předpokladu), ale přesně
tohle náš algoritmus vezme v úvahu. Celý důkaz je v podstatě jen přečtením toho,
co algoritmus dělá, tak už to u (fungujících) dynamik bývá
:).
Ještě se stručně zamysleme nad tolik omílanou časovou složitostí. Předpočet pole
cena nás stojí O(S·(S + P)) – kde S je počet stanic a P počet
zásilek zboží – neboť pro každý úsek j-1:j postupně do fronty naházím a
vyházím až P prvků a při tom kouknu na nejvýše S zastávek. A počítání pole
soucet je s časem na O(N·S2), neboť pro každý počet skenerů
počítám každý úsek i-1:i kouknutím na až S předchozích úseků. S pamětí
se vejdeme do sympatických O(S2 + P).
Za domácí úkol si zkuste řešení upravit tak, aby dělalo to co má, tedy
neodpovídalo jen váhou optimálního řešení, ale ono řešení přímo
vypsalo.
22-4-3 Muzeum (Zadání)
Úloha se dala řešit vylepšeným algoritmem na hledání mostů z grafové kuchařky. Tady si ukážeme jeden trošku elegantnější postup.
Všimneme si, že centrální kamera nemůže ležet na kružnici. To je vidět z toho, že má stupeň rovný počtu komponent a mezi komponentami nemůže vést hrana. Další pozorovací cvičení: Když se jedná o biologické oddělení, tak nám stačí znát kostru grafu (na hranách, které tvoří kružnice, nezáleží, protože ty jsou jen uvnitř komponent). Do třetice si všimneme, že jen z centrálního vrcholu můžeme prohledat (N-1 / K)·(K-1)+1 kamer,1 a to tehdy, když tam nezačínáme s hledáním.
Při řešení budeme nejprve předpokládat, že jsme správně u biologů, pak najdeme centrální kameru a nakonec ověříme, že jsme tam skutečně správně byli. Začneme tedy hledat třeba do hloubky a při návratu počítat navštívené vrcholy. Pokud narazíme na takový, který je podezřelý z centrálnosti, poznamenáme si ho. Teď už jen ověření. Kupodivu stačí to stejné prohledávání. Centrální vrchol si označíme za navštívený a pro každý z jeho sousedů zkontrolujeme, že z něj jde prohledat právě tolik vrcholů, kolik se na slušnou komponentu patří.
1: to je počet všech kamer bez jedné komponenty
22-4-4 Ořez zárodků (Zadání)
Označme si mateřský strom A, odvozený B. Začneme drobným pozorováním: Pokud ve stromě A najdeme posloupnost bratrských podstromů, která odpovídá podstromům synů kořene B, potvrdili jsme odvození B od A. Je-li x kořenem stromu X, jeho bratrským podstromem přirozeně rozumíme podstrom s kořenem y, kde y je bratrem x. Jaký strom zvolit jako mateřský? Zřejmě ten, který obsahuje více vrcholů. Každé „osekání“ pouze vrcholy odebírá. Pokud jich mají po „osekání“ stejně, musí být stromy identické a uvedené pozorování nadále platí.
Jak efektivně hledat posloupnost podstromů synů kořene B v A? Uděláme cimrmanovský krok stranou, vyhneme se znovuobjevování kola a převedeme problém na hledání podřetězce v řetězci. Ano, kuchařku jste si měli přečíst …
Zbývá najít vhodnou reprezentaci stromu pomocí řetězce. Odpověď je triviální
– použijeme uzávorkované výrazy. List je reprezentovaný pomocí (). Každý
jiný vrchol (včetně kořene) pak jako ( =reprezentace 1. syna= =reprezentace 2. syna= …=reprezentace posledního syna= ). Dva malé
stromečky ze zadání této úlohy jsou pak reprezentovány například takto:
((()())()) a (()()()).
Zřejmě každý strom má nějakou reprezentaci. Platí také, že je reprezentací strom jednoznačně určen? To snadno dokážete pomocí indukce. Pro list to platí a dále postupně podle složitosti vrcholu … Zkuste si to rozmyslet. Také platí, že každý správně uzávorkovaný výraz (v běžném slova smyslu) reprezentuje nějaký strom. Pokud tedy vezmeme několik správně uzávorkovaných výrazů a „slepíme“ je za sebe do řetězce q, reprezentují posloupnost nějakých stromů Y1, Y2, …, Yn. Pokud se navíc q vyskytuje v reprezentaci nějakého stromu X, našli jsme uvnitř X interval sousedících bratrských podstromů Y1, …, Yn.
Ať to tedy uzavřeme: Vezměme reprezentaci B a odštípněme vnější závorky (tj. získáme „slepenec“ reprezentací podstromů jeho synů), označme jako q. Pokud nalezneme q v reprezentaci stromu A, platí, že B je odvozený od A, v opačném případě nemůže být B od A odvozen.
Cože? Ještě jste si tu kuchařku nepřečetli a nevíte jak najít q v reprezentaci A? Přece pomocí vynálezu pánů Knutha, Morrise a Pratta … algoritmem KMP.
Čas, paměť? Trvání výroby řetězcové reprezentace stromu a její velikost jsou lineární vzhledem k počtu vrcholů stromu. KMP běží v lineárním čase se součtem délek řetězců (jehly i kupky sena :o) ). Časová i prostorová složitost algoritmu je tedy O(N), kde N budiž součtem počtu vrcholů obou stromů.
22-4-5 Energetické články (Zadání)
Úloha měla přísné limity v zadání, ale samotná data byla většinou přísná jen v jednom parametru, a tak jistě prošla i asymptoticky ne tak dobrá, leč vynalézavá řešení. A tak to u praktických úloh má být!
Pojďme na řešení: nejprve bylo důležité si všimnout, že pokud
zřetězíme dva palindromy za sebe a vznikne další palindrom,
musí se stát, že oba palindromy mají společný „základ“.
Pokud je kratším palindromem ABA, pak delší palindrom
(aby bylo zřetězení palindromem) musí začínat ABA (má tvar ABAx), a protože
delší palindrom je také palindrom, bude i končit ABA (tvar ABAxABA)
a dále pokračujeme stejným argumentem (indukcí). Není pravda, že jeden
je mocninou druhého (například pro ABAABA a ABAABAABA), ale společný
kořen jistě mají.
Hodilo by se nám tedy počítat kořen palindromu, tedy nejkratší řetězec takový, že jeho vhodným umocněním získám celý palindrom. Takový kořen je sám palindromem. Umíme-li kořen najít, pak stačí pro vstupní palindromy vždy najít kořeny, tyto kořeny jednoduše zpracovat (ať už pomocí hashování nebo pomocí setřízení, jako je to předvedeno ve vzorovém řešení) a správně napočítat.
Teď na tu pořádnou práci: jak co nejrychleji spočítat kořen palindromu? Půjdeme na to stejně, jak popisoval Vojta na KSPáckém fóru: budeme postupně procházet řetězec a průběžně si přepočítávat, jak by takový kořen mohl být dlouhý. Zpět se už ohlížet nebudeme – čteme-li Z-té písmenko a myslíme si, že kořen je P znaků dlouhý, podíváme na (Z mod P)-té písmenko a porovnáme. (Vězte, že je to takové písmeno, jež musí být stejné se Z-tým písmenkem, aby opravdu platilo, že kořen má délku P.)
Když se písmenka neshodují, můžeme prodloužit periodu P na Z-1 nebo Z. Nemůže se nám stát, že se nám schovává perioda někde mezi P a Z-1. To se nahlédne podobně jako první pozorování: byla-li by tam taková perioda A, pak v periodě A je 1., A-té, A+1-ní a P-té písmeno shodné. Protože A je menší než Z-1, víme, že A-té písmenko není P-té ani 1., a to nám dá další shodnou dvojici … a nakonec dostaneme, že by všechna písmenka musela být shodná.
Co se týče časové složitosti, tak pokud využijeme chytrou hashovací funkci se zhruba konstantní časovou složitostí na přístup (a pamatujeme si neprázdná políčka), pak se (nikoli v nejhorším případě) dostaneme k O(V + N), kde N je počet řetězců a V je velikost vstupu (sice mohla být až N·K, ale rychleji by to stejně nešlo). Vzorové řešení používá mnoho asymptoticky záludných situací (například porovnávání řetězců nebo jejich třídění zabudovanou knihovnou), ale přesto jsme se jej rozhodli takto zveřejnit. Ukazuje totiž vlastnost mnoha praktických a soutěžních úloh – občas si můžete dovolit zkusit vyměnit nejlepší konstantu či asymptoticky horší složitost za čitelnost a jednoduchost kódu, pokud je hlavní podmínkou „vejít se“ do časového limitu.
22-4-6 Umisťování panelů (Zadání)
Najskôr sa zamyslime nad tým, ako vyzerajú jednotlivé obdĺžniky, ktoré vystupujú v nejakom riešení, a ako ich rýchlo všetkých nájsť.
Tieto obdĺžniky sú najmenšie obdĺžniky, ktoré obsahujú množinu nejakých K bodov. Teda určite platí, že ohraničujúce x-ové a y-ové súradnice každého obdĺžnika sú rovnaké ako príslušné súradnice nejakých bodov, ktoré daný obdĺžnik obsahuje. Pretože inak by sme mohli jednoducho obdĺžnik v príslušnom smere zmenšiť a dostali by sme menší obdĺžnik, obsahujúci tie isté body.
Teda všetkých obdĺžnikov je maximálne O(N4), pretože toľko je kombinácií, ako vybrať ohraničujúce body obdĺžnika. A pre každý obdĺžnik vieme v čase O(N) skontrolovať, či obsahuje práve K bodov.
V skutočnosti však počet všetkých možných obdĺžnikov obsahujúcich K bodov je rádovo menší. Ak totiž máme danú spodnú a hornú y-ovú súradnicu obdĺžnika a tiež ľavú x-ovú súradnicu obdĺžnika, potom existuje nanajvýš jedna možná hodnota x' pre pravú x-ovú súradnicu obdĺžnika tak, že obsahuje K bodov. Pretože obdĺžniky s menšou pravou x-ovou súradnicou ako x' obsahujú menej ako K bodov a obdĺžniky s väčšou pravou x-ovou súradnicou ako x' obsahujú viac bodov ako K.
Teda počet všetkých korektných obdĺžnikov je len O(N3). Ak si naviac na začiatku usporiadame body podľa x-ovej súradnice, tak pre každú kombináciu hornej a dolnej súradnice y a ľavej súradnice x obdĺžnika vieme nájsť odpovedajúcu pravú stranu obdĺžnika v čase O(N). To spravíme jednoducho tak, že budeme postupne pridávať body do obdĺžnika, pokiaľ nedosiahneme počet K.
Ku vzorovému riešeniu však potrebujeme nájsť všetky korektné obdĺžniky rýchlejšie, a to v čase O(N3). To vyriešime metódou „okienka“ (sliding window) nasledovne:
Najskôr si body znova usporiadame podľa x-ovej súradnice. Zafixujeme si hornú a dolnú súradnicu y a následne jedným prechodom nájdeme pravý okraj ku všetkým obdĺžnikom, ktoré majú príslušnú hornú a dolnú y-ovú súradnicu a ďalej budeme teda pracovať len s bodmi ležiacimi v tomto páse.
Najskôr nájdeme štandardným spôsobom (pridávaním bodov, pokiaľ nedosiahneme K) pravý okraj k obdĺžniku, ktorý má ľavý okraj na prvej x-ovej súradnici. Následne sa presunieme na ďalšiu ľavú x-ovú súradnicu a vieme, že príslušný pravý okraj leží napravo od pravého okraja posledného nájdeného obdĺžnika. Teda ho nájdeme znova pridávaním bodov, ale začíname od posledného nájdeného okraju. Všimnime si, že súradnice všetkých ľavých a pravých okrajov nájdených obdĺžnikov navzájom tvoria neklesajúcu postupnosť, a teda pri tomto hľadaní spravíme spolu lineárne veľa práce.
Teraz môžeme pristúpiť k vyriešeniu celej úlohy a zamyslieť sa, čo to znamená nájsť dva disjunktné osovo-paralelné obdĺžniky, pričom každý obsahuje práve K bodov.
V podstate to znamená to, že v každom takomto riešení existuje deliaca horizontálna alebo vertikálna priamka taká, že jeden z obdĺžnikov je na jednej strane tejto priamky a druhý je na opačnej strane priamky.
Bez ujmy na všeobecnosti teda predpokladajme, že pre optimálne riešenie je táto priamka horizontálna. (Vyriešením rovnakej úlohy pre vertikálnu priamku a vybratím lepšieho riešenia dostaneme celkové optimum.)
Teda pre hľadané dva obdĺžniky musí platiť, že horná y-ová súradnica jedného je menšia ako dolná y-ová súradnica druhého.
Pre každú y-ovú súradnicu si teda spočítame najmenší obdĺžnik, ktorý má na tejto pozícii dolný okraj, a taktiež najmenší obdĺžnik majúci na tejto súradnici horný okraj. Následným vyskúšaním všetkých dvojíc dolného a horného okraju nájdeme optimálne riešenie.
Časová zložitosť spočíva z O(N log N) na utriedenie bodov na začiatku, O(N3) na nájdenie všetkých korektných obdĺžnikov a nakoniec O(N2) na vyskúšanie všetkých kombinácií dolného a horného okraja dvoch obdĺžnikov. Teda spolu O(N3).
Pamäťová zložitosť nám vystačí lineárna, ak si pri hľadaní obdĺžnikov súčasne vytvárame aj tabuľku obvodu najmenšieho obdĺžnika majúceho daný horný a dolný okraj, pričom túto tabuľku ihneď po nájdení obdĺžnika zaktualizujeme a samotné obdĺžniky si teda nemusíme pamätať.
22-4-7 Pozdrav z pravěku (Zadání)
Úkol 1: Nabízí se x%∣x, tedy dělit číslo jeho absolutní hodnotou,
ale to selže pro x=0. Lepší je využít toho, že porovnávání vrací 0 nebo 1
a použít (x>0)-(x<0).
Úkol 2: Jelikož APL vyhodnocuje zprava doleva, ι5+1 je totéž co ι6,
tedy vektor 0 1 2 3 4 5. Naproti tomu 1+ι5 je totéž co 1+0 1 2 3 4,
což je podle pravidel o počítání s vektory 1 2 3 4 5.
Úkol 3: ι(2+ι3) → ι(2+0 1 2) → ι(2 3 4), což vytvoří
trojrozměrné pole tvaru 2×3×4 vyplněné čísly od 0 do 23.
Úkol 4: Stačí /⌈/⌈x – nejdříve nám /⌈x dá vektor maxim sloupečků
a z něj si pak druhou redukcí vybereme maximum.
Úkol 5: Všimněme si, že jednička má být právě tam, kde je první souřadnice
(číslo řádku) menší než druhá. Stačí tedy použít direktní součin (ιn)∘.<(ιn).
Úkol 6: Nejprve vytvoříme matici
| ( | 0 | 1 | 2 | 3 | … | n-2 | n-1 | ) |
| n-1 | n-2 | n-3 | n-4 | … | 1 | 0 |
laminací vektorů ιn a (n-1)-ιn. Pak ji stačí transponovat
a operátorem ρ přeformátovat na vektor délky 2n. Celý program
tedy zní (2×n)ρ⍉(ιn)~((n-1)-ιn).
Úkol 7: Nebudeme troškaři, najdeme rovnou všechny společné dělitele zadaných čísel x, y a pak z nich vybereme toho největšího:
a ← 1+ιn |
p ← 0=a∣x |
q ← 0=a∣y |
r ← a×p×q |
d ← /⌈r |
Jak to funguje? Nejprve sestrojíme vektor a obsahující čísla 1,… ,n. Další vektor p obsahuje jen nuly a jedničky, přičemž jedničky jsou přesně na místech dělitelů čísla x (spočítáme zbytky a porovnáme je s nulou). Podobně q indikuje dělitele čísla y. A vektor r vznikne z a vynulováním těch čísel, která nejsou společnými děliteli x a y, takže už stačí najít maximum z jeho prvků.
Program ještě můžeme trochu zkrátit:
/⌈(0=a∣x)×(0=a∣y)×a←1+ιn.
Filip Hlásek vymyslel ještě magičtější řešení:
+/0=y∣x×1+ιy,
zkuste přijít na to, jak funguje. Poradíme vám, že se k tomu hodí rovnost xy=nd, kde d je největší společný dělitel a n nejmenší společný násobek.