Druhá série začátečnické kategorie dvacátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 12. ledna 2015 8:00
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 27-Z2-1: Závorky z cereálií
• 27-Z2-2: Hrnce od Horsta
• 27-Z2-3: Nápis na tričku
• 27-Z2-4: Hořící auto
• 27-Z2-5: Hledání stromů
• 27-Z2-6: Povrch dálnice

Úvodem vás chceme upozornit na nové články o načítání vstupu v Pythonu a jazyce C v naší webové Encyklopedii. Mohly by vám být nápomocné při řešení praktických úloh.

27-Z2-1 Závorky z cereálií (8 bodů)

„Vyřešte hlavolam a pojeďte na exkurzi k německé dálniční policii!“ hlásal slogan na obalu cereálií, které si Kevin koupil k snídani. Po zatáhnutí za papírek na něj z krabice vypadla dlouhá rulička papíru potištěná spoustou různých závorek.

Úkolem bylo odhadnout, kolik nejméně závorek je potřeba přidat, aby výraz byl správně uzávorkovaný (aby se závorky nekřížily a všechny byly správně spárované). Například výraz ()() správně uzávorkovaný je, ale ()( ani ))(( nejsou. „Jaké odhadování?“ řekl si Kevin, „já to spočítám přesně!“

Tvar vstupu: Na vstupu dostanete na jediném řádku posloupnost otevíracích ( a zavíracích ) závorek dlouhou maximálně 100 000 znaků.

Tvar výstupu: Na výstup vypište jedno celé číslo udávající, kolik nejméně závorek je potřeba přidat, aby byl výraz správně uzávorkovaný.

)())

2

(())()

0

Řešení

27-Z2-2 Hrnce od Horsta (10 bodů)

Kevin se Sárou jedou do Německa! Sice si Kevin výhru představoval jinak než jako cestu autobusem plným důchodců, ale aspoň něco. Jejich autobus se teď dokonce zastavil v nějakém nákupním centru a dav se vyhrnul ven s voláním: „Poběžte, uvidíme živého Horsta, Horsta Fuchse!“

Kevin se Sárou se vydali za davem, snadno předešli běžící důchodce a stanuli před pultem plným hrnců s podivným chlapíkem za ním. „Nakupte sadu našich Ultra hrnců! Když si ji koupíte do tří minut, nedostanete jednu sadu navíc, ani dvě sady navíc. Ne, dostanete tři sady navíc a k tomu magnetku na lednici!“

Pamatuje na to, že slíbil dovézt z Německa babičce nějaký dárek, Kevin jednu sadu koupil, a byl obtěžkán několika dalšími. Teď řeší problém, jak poskládat hrnce do sebe, aby v autobuse zabraly co nejméně místa.

Každý hrnec má svůj průměr v centimetrech a dá se do něj vložit jakýkoliv hrnec s menším průměrem, do něhož se opět dá vložit další ještě menší hrnec a tak dál. Kevina by zajímalo, do kolika nejméně „komínků“ může hrnce seskládat.

Tvar vstupu: Na prvním řádku vstupu dostanete číslo N udávající počet hrnců. Na druhém řádku poté bude N přirozených čísel udávajících průměry hrnců. Bude platit, že N ≤ 50 000 a průměry hrnců budou mezi 1 a 700 000.

Tvar výstupu: Na první řádek výstupu vypište číslo K udávající minimální počet komínků, do kterých se dají hrnce seskládat. Na dalších K řádcích pak vypište hrnce v jednotlivých komíncích (v pořadí od největšího hrnce). Pokud existuje více možností poskládání, vypište libovolné z nich.

6
1 6 7 1 6 3

2
7 6 3 1
6 1

Řešení

27-Z2-3 Nápis na tričku (10 bodů)

Kevinova exkurze se konečně dostala do místa, kam se těšil nejvíce – na stanici německé dálniční policie. Nebyl by to ale Kevin, aby se nezatoulal, kam neměl. Ani nevěděl jak, ale ocitl se na průhledné straně poloprůhledného zrcadla a stal se svědkem výslechu.

Policista se zrovna vyptával na nápis na firemním tričku podezřelého. Ale jediné, co dokázal ze svědkyně dostat, bylo: „No víte… já si ten nápis nepamatuji, ale kdyby se k němu přidalo pár písmenek a tahle se přeházela, dalo by to slovo pampeliška, pane policisto. Přísahám vám, já luštím křížovky!“

Policista bezradně rozhodil rukama, vyšel z místnosti na chodbu… a tam potkal Kevina. Kevin tu rozhodně neměl co dělat. Než se na něj ale stihl policista obořit, rozhodl se Kevin rychle improvizovat. Nenapadlo ho však říci nic lepšího než: „Můžu vám pomoci najít ten název firmy.“

Tím si to ale zavařil, protože byl posazen k počítači s databází všech německých firem a teď potřebuje rychle spočítat, kolik různých názvů firem se dá poskládat z vybraných písmen zadaného slova.

Tvar vstupu: Na prvním řádku vstupu dostanete jediné slovo S. Na druhém řádku bude číslo N udávající počet slov ve slovníku a na dalších N řádcích naleznete slova slovníku (na každém řádku jedno). Slov ve slovníku bude maximálně 30 000, všechna slova budou dlouhá nanejvýš 100 znaků a všechna budou tvořena z malých písmen anglické abecedy („ch“ chápeme jako dvě písmena).

Tvar výstupu: Na výstup vypište ta slova ze slovníku, která se dají poskládat z vybraných písmen slova S, na každý řádek právě jedno. Slova vypisujte v pořadí, v jakém se objevila ve vstupním souboru.

pampeliska
4
liska
mapa
zeli
kapka

liska
mapa

Řešení

27-Z2-4 Hořící auto (12 bodů)

„Proč já?“ problesklo Kevinovi hlavou. Jako poděkování za pomoc vzal Semir jeho a Sáru na projížďku po německé dálnici. Ale kdo měl vědět, že po nich bude někdo střílet!

Teď mají poškozené řízení, díru v nádrži, vytéká jim benzín a z vysílačky se ozývá jen: „Kobro 11, jestli zničíte ještě jedno auto, dostanete příště šlapací tříkolku!“ Aby toho nebylo málo, ta vytékající palivová čára za nimi právě vzplanula.

Auto je poškozené tak, že může zatáčet jen doprava, a to vždy jen o pravý úhel. Navíc těsně za ním hoří čára vytékajícího benzínu, a pokud auto znovu překříží hořící čáru, vybuchne. Autonavigace Semirovi vnucuje nějaký plán cesty a Kevin by chtěl vědět, jak moc je bezpečná.

Tvar vstupu: Na prvním řádku vstupu bude číslo N a na druhém pak řada N celých kladných čísel. Znamenají, že auto ujede a₁ metrů rovně, zabočí doprava, ujede a₂ metrů rovně, zabočí doprava, ujede a₃ metrů rovně, zabočí doprava a tak dále. Bude platit, že N ≤ 2 000 000, a délky jednotlivých úseků budou nanejvýš 10⁹ metrů.

Tvar výstupu: Na jediný řádek výstupu uveďte, po kolika zatáčkách auto překříží hořící dráhu (za překřížení počítáme i dotyk), zatáčky počítejte od jedničky. Pokud k překřížení nedojde, vypište na výstup nulu.

9
1 2 2 4 3 5 2 2 2

7

K této úloze jsme na Dnu otevřených dveří MFF UK ukázali drobnou nápovědu. Abychom byli spravedliví k ostatním, kteří třeba na DODu být nemohli, můžete se podívat na video se záznamem z přednášky.

Řešení

27-Z2-5 Hledání stromů (12 bodů)

Kevinovi se z drsné jízdy autem z minulé úlohy udělalo trochu špatně, a tak se po návratu na policejní stanici posadil do nejbližšího křesla a pro uklidnění si začal na papír kreslit nějaké body a čáry mezi nimi. Dalo by se říci, že si kreslil na papír grafy.

Sára se mezitím někam zatoulala, a tak jí Kevin jeden obzvláště pěkný graf poslal SMSkou (třeba jako seznam sousedů, tedy pro každý bod seznam, se kterými jinými body je tento bod spojený čárou). Sáru by teď zajímalo, jestli je graf, který dostala, stromem – tak se říká grafům, které jsou souvislé (z každého vrcholu se dá dostat do každého jiného) a neobsahují žádný cyklus.

Zkuste pečlivě popsat postup, jak to algoritmicky zjistit. Graf si můžete představit zadaný seznamem sousedů jako na ukázce níže. Pokud budete chtít, můžete si i rozmyslet, jestli se postup nějak změní, pokud graf dostaneme jako matici sousednosti (ale na plný počet bodů stačí zamyslet se jen nad verzí se seznamem sousedů).

Pokud tápete v pojmech grafů, stromů a jejich reprezentace, podívejte se do naší kuchařky o základních algoritmech.

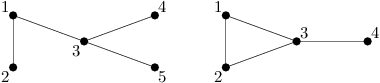
Příklad: Pro grafy níže: levý graf je stromem, pravý ale není, jelikož obsahuje cyklus 1, 2, 3.

1: 2,3				1: 2,3
2: 1				2: 1,3
3: 1,4,5			3: 1,2,4
4: 3				4: 3
5: 3

Řešení

27-Z2-6 Povrch dálnice (14 bodů)

Nadešel čas, kdy se měli Kevin se Sárou zase vrátit z Německa domů. Semir věnoval Kevinovi na památku zachráněný volant z jeho služebního auta a ještě naposled je vzal na procházku na místo, kde se opravovala dálnice po jejich zběsilé jízdě z předchozích úloh.

Povrch byl pokrytý obroušenými zbytky gumy, olejem a spálenou klikatící se čárou. Jeden z policistů obcházel místo s kolečkem na měření vzdáleností a počítal, kolik metrů čtverečních dálnice bude potřeba vyčistit a opravit.

Policista chodí pravoúhle vždy o celé metry a jeho kroky by se daly popsat třeba pomocí světových stran jako posloupnost 5×jih, 2×západ, 3×sever, atd. Navíc nikdy nepřekříží svoji dřívější cestu a nakonec se vrátí zpátky do místa, odkud vyšel. Obejde tedy obvod nějakého uzavřeného obrazce.

Kevina by teď zajímalo, jak velký kus dálnice to vlastně je, tedy jaký má obsah.

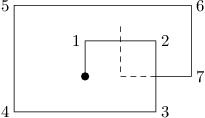
Příklad: Následující obrazec mohl vzniknout tím, že policista vyrazil po níže uvedené trase. Obsah obrazce je 7 m².

1S,2V,1S,2V,1J,1Z,2J,1Z,1S,1Z,1J,1Z,1S

Řešení