Třetí série začátečnické kategorie dvacátého sedmého ročníku KSP

Celý leták, který posíláme také papírově, v PDF.

• Termín série: 9. března 8:00
• Odevzdávání: elektronicky přes Odevzdávátko
• Jak sepsat řešení: viz ukázková úloha MO-P
• Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.

Zadání úloh

• 27-Z3-1: Kevin nabíječ, s.r.o.
• 27-Z3-2: Nedej vitagen
• 27-Z3-3: Superstromy
• 27-Z3-4: Robo Rally
• 27-Z3-5: Dřevěná slacklajna
• 27-Z3-6: Red Bull dává křídla

Úvodem vás chceme upozornit na nové články o načítání vstupu v Pythonu a jazyce C v naší webové Encyklopedii. Mohly by vám být nápomocné při řešení praktických úloh.

27-Z3-1 Kevin nabíječ, s.r.o. (8 bodů)

Většina Kevinových spolužáků velice aktivně používá smartphone. Možná ale až moc, protože se jim pořád vybíjí. Kevin je na rozdíl od nich podnikavý typ, a tak dostal nápad. Začne podnikat s jejich nabíjením. Ve třídě však mají jen jednu zásuvku, tak Kevin skočil do elektra a koupil prodlužovačky s různými počty výstupů. Nyní by jej zajímalo, kolik nejvíce smartphonů zároveň může nabíjet, pokud prodlužovačky zapojí optimálně.

Tvar vstupu: Na prvním řádku vstupu dostanete číslo N (1 ≤ N ≤ 1 000 000) udávající počet Kevinových prodlužovaček. Na druhém řádku bude N čísel oddělených mezerou udávající počty zdířek jednotlivých prodlužovaček. Všechny prodlužovačky budou mít nejméně nula a nejvíce sto zdířek.

Tvar výstupu: Na výstup vypište jediné číslo udávající nejvyšší možný počet volných zdířek, kterých Kevin může optimálním zapojením prodlužovaček dosáhnout.

2
3 5

7

Řešení

27-Z3-2 Nedej vitagen (10 bodů)

Kevinova sestra Zuzka dostala od Ježíška písmenkovou skládačku, pomocí které se učí číst slova popředu… a taky pozpátku. Z písmenek poskládala několik slov a všimla si, že některá se čtou popředu stejně jako jiná pozpátku. Hned se běžela pochlubit Kevinovi a zeptala se jej, které nejdelší slovo vypadá stejně jako jiné pozpátku.

Tvar vstupu: Na prvním řádku vstupu dostanete číslo N, počet slov, které Zuzka poskládala. Na dalších N řádcích bude jedno slovo složené z malých písmen anglické abecedy o maximálně 100 znacích. Slov bude maximálně 100 000.

Tvar výstupu: Na výstup vypište nejdelší slovo, které má mezi slovy na vstupu i svou verzi napsanou pozpátku. Pokud takových slov existuje více, vypište to, které je lexikograficky nejmenší (tj. ve slovníku by bylo napsané jako první).

5
kecup
ves
vrabec
pucek
sev

kecup

Řešení

27-Z3-3 Superstromy (10 bodů)

Kevinův kamarád Petr bude pořádat párty ve své nové zahradě. Ještě předtím by v ní ale chtěl vysadit N rychlorostoucích superstromů, přičemž o každém přesně ví, kolik dní po zasazení doroste. Se sázením je docela práce, a tak každý den zvládne zasadit právě jeden superstrom. Párty bude uspořádána právě den poté, co doroste poslední ze superstromů. Petr se teď potřebuje s Kevinem poradit a zjistit, kdy nejdříve párty může uspořádat.

Tvar vstupu: Na prvním řádku vstupu bude číslo N udávající celkový počet superstromů (1 ≤ N ≤ 1 000 000). Na druhém řádku bude N čísel oddělených právě jednou mezerou udávající doby růstu jednotlivých superstromů ve dnech. Tyto hodnoty budou v rozsahu 1 až 1 000.

Tvar výstupu: Na výstup vypište číslo dne, na kdy Petr může naplánovat párty, pokud superstromy bude sázet v optimálním pořadí. První den, kdy Petr sází, má číslo 1.

4
3 6 7 2

9

Řešení

27-Z3-4 Robo Rally (12 bodů)

Kevin dostal k Vánocům deskovou hru Robo Rally. Zjednodušeně to je hra, kde se na herní ploše o rozměrech W ×H pohybuje N robotů. Na začátku každý robot začíná na své pozici a je natočený jedním ze čtyř směrů. Pak roboti střídavě plní příkazy, v jeden moment plní příkaz vždy pouze jeden robot. Příkazy mohou být tří typů: „otoč se doleva“, „otoč se doprava“ a „popojdi rovně o jedno políčko“.

Příkazy jsou předem určené. Každý příkaz v sobě obsahuje číslo robota, pro kterého je určen, akci, kterou má robot vykonat, a počet opakování pro danou akci. Například zápis 3 K 5 znamená, že robot číslo 3 udělá 5 kroků vpřed, 2 L 1, že robot 2 se jednou otočí o 90 ° doleva a 4 P 3, že robot 4 se třikrát otočí o 90 ° doprava.

To ale není všechno. Roboti občas do sebe můžou narazit nebo dojet na kraj herní plochy. Pokud robot narazí na kraj, zůstane na stejném políčku. Pokud narazí do jiného robota, tak jej posune o jedno políčko směrem, kterým jede. Stejně tak pokud narazí do řady robotů, tak daným směrem posune celou řadu. Pokud je ale na konci řady okraj desky, celá řada se zastaví.

Kevin poskládal na desku roboty do počáteční pozice a vytáhl pro ně M kartiček s příkazy. Zajímalo by ho, jak pozice na desce bude vypadat po vyplnění všech M příkazů v pořadí, v jakém je vytáhl. Pomůžete mu to zjistit?

Tvar vstupu: Na prvním řádku vstupu budou čtyři čísla: W, H, N, M udávající postupně šířku a výšku desky, počet umístěných robotů a počet příkazů. (1 ≤ W,H ≤ 100, 1 ≤ N,M ≤ 2500 a N ≤ W·H)

Dalších N řádků udává pozice jednotlivých robotů, každý je ve tvaru X Y S, kde 0 ≤ X ≤ W-1, 0 ≤ Y ≤ H-1 a S je jeden ze znaků S, V, J, Z, tj. světová strana, na kterou je robot otočený. Souřadnici [0,0] považujeme za severozápadní roh hrací desky. Pozice robotů jsou navzájem různé.

Na dalších M řádcích jsou definovány příkazy. Příkaz je tvaru R P I, kde R představuje číslo robota (0 ≤ R ≤ N-1), P znak příkazu (L pro rotaci doleva, P pro rotaci doprava a K pro pohyb dopředu) a I počet opakování (1 ≤ I ≤ 1 000 000 000).

Tvar výstupu: Na výstup vypište N řádek udávající koncové pozice robotů. Na i-tém z nich vypište x-ovou a y-ovou souřadnici a natočení robota číslo i a to ve stejném formátu jako na vstupu.

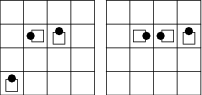
4 4 3 3
0 3 S
1 1 Z
2 1 S
0 K 2
0 P 1
0 K 10

1 1 V
2 1 Z
3 1 S

Hrací deska na začátku a na konci hry vypadá následovně:

Řešení

27-Z3-5 Dřevěná slacklajna (12 bodů)

Kevin a Sára rádi chodí po slacklajně, jen jim to zatím moc nejde. A tak se rozhodli, že si postaví vlastní, jednodušší, ze dřeva. K dispozici mají n prken o délkách d₁, … , d_n. Dvě prkna k sobě můžou přidělat (spojit za konce) pod libovolným úhlem. Z prken by si chtěli postavit co nejdelší okruh (myšleno mnohoúhelník), po kterém by mohli chodit kolem dokola.

Navrhněte pro ně co nejefektivnější algoritmus, který pro zadané délky prken spočítá největší obvod okruhu, který je možné z prken postavit. Okruh může být jak konvexní, tak nekonvexní, ale nesmí sám sebe protínat. Není nutné použít všechna prkna. Nezapomeňte pořádně zdůvodnit, proč algoritmus funguje a proč počítá tak, jak počítá.

Všechna prkna mají stejnou, zanedbatelnou šířku, tedy s nimi můžete pracovat jako s úsečkami.

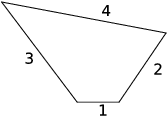
Například pro prkna délek 15, 1, 2, 3, 4 je maximální obvod 1 + 2 + 3 + 4 = 10. Zbylé prkno použít nelze. Výsledný okruh může vypadat například takto:

Řešení

27-Z3-6 Red Bull dává křídla (14 bodů)

„Už nikdy nebudu pít!“ pronesl Kevin po tom, co se na Nový rok probudil u sebe v posteli. „Aspoň ne Red Bull! … Bože, to byla zas cesta domů!“

To byl takhle Kevin na silvestrovské párty u Petra a na závěr, aby měl dost síly dojít domů, si dal čtyři Red Bully. A šlo se. A taky skákalo. Vlastně každý druhý krok byl skok.

Přesněji šel Kevin po takové čtvercové síti velké W×H ze startu na políčku [x_s, y_s] do cíle na políčku [x_c, y_c]. Každý svůj lichý krok skákal, tj. hýbal se jako šachový kůň a každý svůj sudý krok normálně šel, tj. hýbal se jako šachový král. Navrhněte algoritmus, který Kevinovi najde nejkratší cestu ze startu do cíle, pokud cestuje za těchto podmínek.

Jen připomeneme, že skok šachového koně je vždy posunem o dvě políčka v jedné souřadnici a o jedno políčko v souřadnici druhé. Šachový král se může pohnout na jedno z osmi sousedních políček.

Například optimální cesta mezi protějšími rohy šachovnice 6×5 má 4 kroky a vypadá takto:

Řešení