Druhá série začátečnické kategorie dvacátého sedmého ročníku KSP
Celý leták v PDF.
Řešení úloh
- 27-Z2-1: Závorky z cereálií
- 27-Z2-2: Hrnce od Horsta
- 27-Z2-3: Nápis na tričku
- 27-Z2-4: Hořící auto
- 27-Z2-5: Hledání stromů
- 27-Z2-6: Povrch dálnice
 27-Z2-1 Závorky z cereálií (Zadání)
27-Z2-1 Závorky z cereálií (Zadání)
Dostali jsme několik závorek. A naším úkolem je zjistit minimální počet závorek, které musíme doplnit, aby výsledná posloupnost byla správně uzávorkovaná. Tento počet je roven počtu nespárovaných závorek uvnitř posloupnosti.
Nespárované závorky budeme hledat tak, že projdeme pole a cestou si budeme
pamatovat počet zatím nespárovaných závorek. Řekneme si, že za každou otevírací
závorku '(', na kterou narazíme, zvýšíme počet zavíracích závorek ')' potřebných
k doplnění. Tento počet nazveme P. Analogicky nám závorky ) budou P
snižovat. A po průchodu máme v P uložený počet závorek ), které musíme
doplnit, abychom měli všechny ( v pořádku.
Ještě nám zbývá dořešit počet otevíracích závorek k doplnění. Ty budeme počítat v proměnné L. Proměnnou L zvýšíme vždy, když při průchodu najdeme zavírací závorku, ale nemáme žádnou otevírací, se kterou bychom ji spárovali.
Na konci průchodu máme v P uložen počet pravých a v L počet levých závorek, které je potřeba doplnit do posloupnosti, aby byla správně uzávorkovaná. Celkový počet pak získáme součtem P + L.
Časová složitost tohoto algoritmu je O(n), kde n je velikost vstupu. Tedy lineární, protože nám na zjištění výsledku stačí jenom jeden průchod zadaného vstupu. Paměťová složitost záleží na načítání vstupu. Pokud bychom načítali právě jeden znak, tak by paměťová složitost byla konstantní. Ale pro naše vzorové řešení je paměťová složitost lineární, protože si celý vstup pamatujeme najednou.
 27-Z2-2 Hrnce od Horsta (Zadání)
27-Z2-2 Hrnce od Horsta (Zadání)
Abychom pomohli hrnce poskládat, budeme muset vyřešit několik podproblémů a začneme tím, že si posloupnost načteme do paměti. Po načtení do paměti posloupnost setřídíme (ve vzorovém řešení je setříděna vzestupně). Nyní musíme udělat ještě dvě věci. Spočítat, kolik hromádek hrnců budeme mít, a poté nějaké vytvořit. To uděláme pěkně postupně.
Spočítání počtu hromádek hrnců není nijak těžké a zvládneme ho za jeden průchod. Budeme si pamatovat, kolik hromádek právě teď máme (na začátku máme právě jednu o právě jednom hrnci – tom prvním), a počet hromádek zvětšíme pokaždé, když v posloupnosti objevíme více hrnců stejného průměru za sebou, než je počet hromádek. Pokud tedy máme zatím tři hromádky o maximálním průměru deset a narazíme na sedm hrnců s průměrem jedenáct, budeme potřebovat hromádek sedm, do tří hrnců dáme ty tři menší hromádky a čtyři nové musíme založit. Toto zvládneme v O(N).
Nyní potřebujeme nějaké hromádky vytvořit. To můžeme udělat například takto – víme, kolik hromádek budeme potřebovat, takže si je napřed založíme (ve formě spojových seznamů či dostatečně velkých polí). Pokaždé načteme všechny hrnce stejné velikosti a přidáme je po jednom do hromádek. Pokud byl hrnec dané velikosti jen jeden, přidáme ho jen do první, pokud byly dva, přidáme je do první a druhé, atd. Na konci jen hromádky vypíšeme.
V našem příkladu máme tedy maximálně sedm hrnců o stejném průměru. Založíme si tedy sedm hromádek a všechny unikátní hrnce dáme do první, hrnce s průměrem deset byly tři, ty tedy rozházíme po jednom do prvních třech hromádek a poté již sedm hrnců s průměrem jedenáct dáme po jednom do všech sedmi.
Vypsání opět zvládneme v lineárním čase, a tudíž nejnáročnější částí našeho programu je třídění, které seběhne v čase O(N log N). To je tedy časová složitost vzorového řešení, nicméně ani pomalejším řešením se složitostí O(N2) by vstupy neměly trvat o mnoho déle. Paměti spotřebujeme lineárně, pouze načteme vstup a poté vytvoříme hromádky. Paměťová složitost je tedy O(N).
 27-Z2-3 Nápis na tričku (Zadání)
27-Z2-3 Nápis na tričku (Zadání)
Tato úloha mohla na první pohled vypadat složitě, ve skutečnosti je přímočará. Stačilo si spočítat četnost jednotlivých písmen. Jak na to?
Pořídíme si pole 26 čísel – tolik je písmen anglické abecedy, kterou používáme.
Potom stačí přečtené slovo vzít znak po znaku, a patřičný chlívek pole zvětšit
o jedna. V drtivé většině programovacích jazyků se dá k řetězci přistupovat
jako k poli znaků, tj. dívat se na jeho jednotlivé znaky. A většina jazyků má
též funkce pro převod znaku na číslo, třeba podle ASCII tabulky. Například
v jazyce C je znak a číslo to samé, rozlišíte je až podle použití. Proto
stačí od daného znaku odečíst 'a' a máme index do pole četností. Podobný
trik bude fungovat skoro všude.
Když už si umíme spočítat četnosti znaků, spočítáme si je nejprve pro slovo S ze zadání. To je jediné, co si potřebujeme pamatovat. Pak už stačí pro každé slovo spočítat četnosti, jedním cyklem ověřit, jestli se každý znak vyskytuje nejvýše tolikrát, kolikrát se vyskytuje v S. Pokud ano, vypíšeme ho, jinak pokračujeme.
Na závěr jen dodáme, že tabulce četnosti se obvykle říká histogram. Také doufáme, že jste si všimli opravdového seznamu německých firem v jednom ze vstupů.
 27-Z2-4 Hořící auto (Zadání)
27-Z2-4 Hořící auto (Zadání)
Úloha se na první pohled může jevit jako problém hledání průsečíků přímek, což je docela obtížný problém. Zkusme si to ale nejdřív nakreslit. Těch čar může být hodně, kreslit to rukou by trvalo dlouho. Nedal by se k tomu využít počítač?
Dal. V některých programovacích jazycích existují knihovny na takzvanou želví grafiku. Želva tam dělá to samé, co auto. Chodí rovně, zatáčí a přitom za sebou kreslí čáru. Dají se tím kreslit všelijaké pěkné obrázky. Tato úloha je opendatová, řešení můžeme vytvořit, jak chceme. Necháme tedy želvu, aby nám nakreslila obrázek, potom se na něj podíváme a zjistíme, po které zatáčce auto vybuchlo.
Program – želví grafika (Python 3)
Pár bodů se tímto řešením dalo získat, v některých vstupech ale bylo čar hodně, takže to nešlo tak lehce. Vykreslováním ovšem zjistíme, že díky pravoúhlému zatáčení se tento problém dá řešit mnohem jednodušeji.
Pomalé, ale přímočaré řešení
Jedno z nejpřímočařejších řešení je pamatovat si všechny čáry a počítat, jestli se nová neprotne s nějakou předchozí.
Díky tomu, že čáry jsou pravoúhlé, tak to, zda se dvě přímky protínají, se dá určit velice snadno. Čáry budeme mít reprezentované jako dvě dvojice bodů, tedy [xz, yz], [xk, yk] (index z je začátek, k konec, a navíc zajistíme, aby platilo, že xz ≤ xk a to stejné pro y).
Pak pro každou vodorovnou přímku (to je ta, pro kterou je yz = yk) zjistíme, jestli xz ≤ xzi ≤ xk a yzi ≤ yz ≤ yki, kde i ukazuje na i-tou čáru. Obdobně to provedeme pro všechny svislé přímky, jen ve formuli prohodíme x a y.
To je ale pomalé, protože pro každou čáru musíme otestovat i všechny předchozí, z toho plyne časová složitost O(N2).
Řešení přes velikost volného prostoru
Na první pohled vidíme, že křivka vzniklá jízdou auta může být spirála ze středu ven (té budeme říkat zvětšující se), nebo spirála z vnějšku do středu (té budeme říkat zmenšující se). Také se může stát, že chvíli křivka bude zvětšující se spirála, a pak přejde do zmenšující se spirály. Důležité je, že jakmile se auto dostane do zmenšující se spirály, pak už se z ní nedostane, protože by nutně překřížilo křivku, po které již jelo, a tedy by vybuchlo.
Nejprve si pojďme rozebrat ty dva jednodušší případy, tedy pouze zvětšující se spirálu a pouze zmenšující se spirálu. Pro zvětšující se spirálu platí, že dokud auto v daném směru (myšleno vodorovně, nebo svisle) ujede více než minule (tedy pokud délka aktuální čáry je delší než délka čáry o dva kroky dříve), pak nemůže protnout křivku. Pro zmenšující se spirálu obdobně platí, že dokud v daném směru ujede méně než minule, pak nemůže protnout křivku. Problém nastává, když přecházíme ze zvětšující se spirály do zmenšující se. Tehdy si potřebujeme spočítat, kolik místa máme v kolmém směru na směr, kterým jsme zrovna jeli (tedy jak dlouhá je čára o krok dříve). V aktuálním směru je právě tolik místa, kolik jsme ujeli.
Tehdy mohou nastat dvě možnosti:
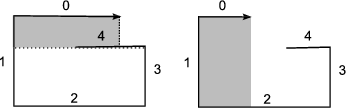
Na obrázcích je šedé místo prostor, ve kterém se může nacházet zmenšující se spirála. Tento prostor si uložíme jako minulý v kolmém směru (tedy jako délku čáry o krok dříve), tedy jakoby zmenšíme vzdálenost, kterou jsme minule urazili v kolmém směru (tento krok nám mírně zjednodušší implementaci).
A to je nejsložitější část. Z obrázků a po rozmyšlení implementace je vidět, že nám stačí si pamatovat posledních pět čar, což můžeme snadno udělat pomocí pole délky 5 a modulení. Pozor na to, že v některých programovacích jazycích záporné číslo modulo kladné je záporné číslo, což my nechceme. Jednoduše přičteme 5, protože tím výsledek neovlivníme (ve smyslu, že 5 mod 5 = 0). Přitom zamezíme tomu, abychom dostali záporná čísla. Druhá možnost je ukládat si čáry zprava doleva, tedy že délka minulé čáry je na pozici (aktualni + 1) mod 5, předminulé na (aktualni + 2) mod 5, …
Nyní ještě zbývá vymyslet, v kterém „módu“ začínat. Jelikož zatím nemáme žádné čáry, tak jistě první i druhá bude vést na zvětšující se spirálu, tedy můžeme začít v módu zvětšující se spirály.
Ještě se zamyslíme nad časovou složitostí. Pokud jsme v módu zvětšující se spirály, tak provedeme jen jedno porovnání, to stejné pro zmenšující se spirálu. Přechod ze zvětšující se do zmenšující se spirály nastane maximálně jednou a práce tam provedeme jen konstantně (podíváme se maximálně na pět posledních a z nich spočítáme volné místo). Tedy každou čáru umíme vyhodnotit v konstantním čase (O(1)), čar je N, a proto časová složitost je O(N).
Program – zmenšování volného prostoru (C)
Ukážeme vám i další naprogramované řešení. Základní idea je podobná, avšak v tomto řešení neuvažujeme o dvou různých spirálách, ale jen se díváme na pět posledních čar. Více detailů naleznete v komentářích zdrojového kódu.
Program – pět posledních čar (C)
 27-Z2-5 Hledání stromů (Zadání)
27-Z2-5 Hledání stromů (Zadání)
Pozrime sa na jednoduché prirovnanie. Graf si predstavíme ako mesto. Medzi každými dvoma križovatkami (vrcholmi) existuje len jedna cesta – to znamená, že tam neexistujú cykly, inak by bolo viacero spôsobov ako sa z jednej križovatky dostať do druhej. Ako keď sa v kruhu môžeme vybrať dvoma smermi. Mesto začneme prehľadávať pred domom, v ktorom bývame. Ak z neho vedie viac ciest, tak si vyberieme ľubovoľnú. Ak len jedna, tak sa vyberieme ňou. Vždy, keď prídeme na križovatku, vyberieme si cestu, ktorou sme ešte nešli. Ak dôjdeme na križovatku, z ktorej vedie jediná cesta a to je tá, ktorou sme prišli, tak sa ňou vrátime o križovatku späť. Ak na križovatke nájdeme cestu, ktorou sme ešte nešli, tak sa ňou vydáme. Ak nenájdeme, tak sa vrátime po ceste, ktorou sme sa prvýkrát dostali k aktuálnej križovatke. Bude to cesta k predchádzajúcej križovatke smerom k domovu.
Náš postup zhrnieme do dvoch krokov:
- ak existuje z križovatky cesta, ktorou sme ešte nešli, tak sa ňou vydáme a dôjdeme na ďalšiu križovatku
- ak taká cesta neexistuje, tak sa vrátime o križovatku „vyššie“
K tomu nám poslúži rekurzia. Každú časť mesta prehľadávame rovnakým spôsobom. Vždy keď prídeme na križovatku, tak vykonáme uvedené kroky. Skončíme vtedy, ak už nemáme kam ísť.
Takéto mesto s križovatkami a cestami predstavuje graf. Ak naše mesto neobsahuje cykly a je súvislé, potom musí byť stromom. Ak sa v grafe vyskytuje cyklus, tak sa na niektorú križovatku vrátime opäť a to po inej ceste, ako sme z tej križovatky odišli. Teda v grafe vedie hrana do vrcholu, ktorý sme už raz navštívili. Taktiež je potrebné v každom vrchole vedieť, z ktorého vrcholu sme doň prišli. Do predchádzajúceho už navštíveného vrcholu vedie hrana, no hrana naspäť netvorí cyklus. Na koniec overíme, či je graf súvislý. Spýtame sa o každej križovatke, či sme na nej boli. S týmito splnenými podmienkami je graf určite stromom.
Na koniec si rozmyslíme časovú a pamäťovú zložitosť riešenia. Počet križovatiek si označíme ako N a počet hrán ako M. Načítanie vstupu nám zaberie čas O(N + M). Prehľadanie celého grafu do hĺbky nám zaberie taktiež čas O(N + M). Je to preto, že v rekurzii každý vrchol navštívime maximálne raz a každou hranou prejdeme maximálne dva krát (tam a späť). Keďže si pamätáme celý graf a počas prehľadávania si naviac ešte pamätáme, ktoré vrcholy sme navštívili, pamäťová zložitosť bude taktiež O(N + M).
Môžme ešte uvažovať prípad, že vstupný graf už máme uložený v pamäti a tá sa do výslednej pamäťovej zložitosti nezapočítava. Keďže strom má vždy N - 1 hrán, stačí nám na začiatku overiť, či táto podmienka platí (a následne graf prehľadať). Prehľadávanie grafu o N - 1 hranách a N vrcholoch nám zaberie čas O(N). Ďalej si počas prehľadávania musíme pamätať, ktoré vrcholy sme navštívili. Preto pamäťová zložitosť v tomto prípade bude O(N).
Drobná poznámka: Ak načítavame vstup a vieme dopredu počet vrcholov (N), potom nám stačí prečítať iba prvých N - 1 hrán. Ak je hrán na vstupe menej, graf bude nesúvislý. Ak vstup obsahuje viac hrán, potom graf bude obsahovať cyklus. Ak nemusíme prečítať pri riešení úlohy celý vstup, môžme ho po N - 1 hrán zarezať a tým docieliť časovú zložitosť O(N) aj v takomto prípade.
Pár slov k bonusu – graf zadaný maticou susednosti: Susedia vrcholu X v takejto tabuľke sú tí, ktorí na pozícii [X, i] pre i od 1 do N majú hodnotu „1“. Teda susedov nemáme v zozname, ale zapísaných v matici. Graf budeme prehľadávať úplne rovnako. Matica má veľkosť NxN, teda načítavanie vstupu ako aj pamäťová zložitosť bude O(N2). Zistenie všetkých susedov jedného vrcholu znamená prejsť jeden riadok tabuľky, čo je N položiek. Pri prehľadávaní do hĺbky potrebujeme zistiť všetkých susedov pre každý vrchol. Časová zložitosť prehľadávania bude teda O(N2).
Ak budeme uvažovať prípad, že maticu už máme načítanú v pamäti, potom sa nám pamäťová zložitosť zlepší na O(N) (nerátame do toho pamäťovú zložitosť vstupu). Je to preto, že si stačí pamätať, ktoré vrcholy sme už navštívili a ktoré ešte len navštívime. Časová zložitosť sa ale kvôli zisťovaniu susedov nezmení a bude aj v tomto prípade O(N2).

 27-Z2-6 Povrch dálnice (Zadání)
27-Z2-6 Povrch dálnice (Zadání)
Pro začátek si představme, že obrazec je nakreslený v souřadnicovém systému nad osou x. Hlavní myšlenkou je, že budeme přičítat a následně odečítat obsahy obdélníčků. Lépe je to vidět na následujících obrázcích. Obdélníčky vlevo přičítáme a vpravo odečítáme.
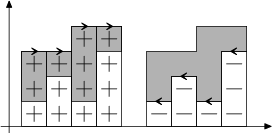
Představu už máme, tak si to pojďme lépe popsat. Budou nám stačit dvě proměnné y a S. Proměnná y, jak již prozrazuje její název, odpovídá naší pozici na ose y. V proměnné S si budeme postupně počítat obsah obrazce. Při pohybu na sever k y jednoduše přičteme ušlou vzdálenost a na jih zase odečteme. Pohyb na východ o vzdálenost l vymezí obdélníček o rozměrech l ×y, jehož obsah l ·y přičteme do S. Při cestě na západ naopak obdélníček odečteme.
Po zpracování celého vstupu máme obsah obrazce v proměnné S. Ještě se nám může stát, že plocha vyjde záporně. To nastane v případě, že jsme obrazec obcházeli proti směru hodinových ručiček. Směr nás ale nezajímá, takže výsledkem je absolutní hodnota S.
Možná se ptáte, jakou nastavit hodnotu y na začátku, když neznáme souřadnice startu. V podstatě je to jedno, neboť to pouze znamená posun osy x, a tedy zvětšení všech obdélníčků o konstantu. Máme však zaručeno, že končíme na startu, takže ke každému přičtenému obdélníčku máme jeden odečtený. Tudíž jsme konstantu vždy jednou přičetli a jednou odečetli, což výsledek nikterak neovlivní.
Dokonce ani nepotřebujeme, aby bylo y po celou dobu kladné. U obdélníčků pod osou x nám stačí prohodit, kdy se obsah přičítá a odečítá. Protože y je záporné, vyjde i hodnota l ·y záporně. Původně při pohybu na západ obsah odečítáme, to tedy znamená, že odečteme zápornou hodnotu. Tím jsme ovšem dostali přičítání. Stejně získáme odečítání obsahu při pohybu na východ (přičítáme zápornou hodnotu).
Paměťová složitost je konstantní, protože vstup nikam neukládáme, ale rovnou jej zpracováváme během čtení. Časová složitost je lineární, jelikož se nikde nezdržujeme a pro každý pohyb provedeme pouze jednoduchou operaci.