Druhá série začátečnické kategorie dvacátého osmého ročníku KSP
Celý leták, který posíláme také papírově, v PDF.
- Termín série: 11. ledna 2016 v 8:00
- Odevzdávání: elektronicky přes Odevzdávátko
- Jak řešit: viz Návod na teoretické úlohy a Návod na praktické úlohy
- Dotazy ohledně zadání: posílejte na ksp@mff.cuni.cz, nebo se ptejte na Discordu KSP.
Zadání úloh
- 28-Z2-1: Před muzeem
- 28-Z2-2: Práce pro Sáru
- 28-Z2-3: Byli jsme tři
- 28-Z2-4: Rozsypaná turbína
- 28-Z2-5: Příkop u Tří soutěsek
- 28-Z2-6: Kalamita
28-Z2-1 Před muzeem (8 bodů)
„Hurá, jdeme na exkurzi!“ znělo třídou stojící před hlavním vchodem leteckého muzea. Učitelky obcházely v řadě stojící žáky a vybíraly z nich skupinky, které půjdou pohromadě.
Papírek se jmény, který dostala Kevinova učitelka, se ale cestou rozmočil a byla čitelná jen první písmenka křestních jmen. Učitelka si sice pamatovala, že vybraní žáci byli zapsaní v abecedním pořadí podle příjmení, ale nepamatovala si, kdo to přesně byl.
Seřadila si tedy své žáky podle abecedy a teď hledá alespoň nějakou skupinku, u které by souhlasila první písmena křestních jmen i pořadí (druhý na papíře musí stát v řadě až za prvním a tak dále).
Tvar vstupu: Na vstupu dostanete na prvním řádku dvě čísla: počet žáků ve skupince a celkový počet žáků ve třídě. Na druhém řádku pak první písmena křestních jmen žáků ve skupince a na třetím první písmena křestních jmen všech žáků (tak, jak stojí za sebou v řadě).
Tvar výstupu: Vypište mezerou oddělené pořadí vybraných žáků (žáky číslujeme od jedničky). Pokud takových výběrů existuje více, vypište libovolný z nich.
3 8 JAJ AJJBAJAJ
3 5 8
Poznámka: Výběr 3 5 6 nebo třeba 2 5 6 fungují taky, 2 1 3 ne,
protože žáci nestojí v tomto pořadí za sebou.
28-Z2-2 Práce pro Sáru (10 bodů)
V muzeu se ke Kevinovi připletla Sára a chtěla si s ním povídat. Kevin fascinovaný pohledem na motor z letadla si ale povídat nechtěl, a tak dal Sáře úkol.
Napsal jí na papír číslo a řekl jí, aby prováděla následující operace, než se dostane k jedničce:
- Pokud je číslo sudé, vyděl ho dvěma.
- Je-li liché, vynásob číslo třemi a přičti jedničku.
Doufal, že Sáru na chviličku zabavil, ale než se stihl otočit zpátky k motoru z letadla, tak už Sára jásala, že dosáhla jedničky. Kevin asi zvolil nějaké jednoduché číslo, chtěl by jí teď zadat nějaké těžší. Ideálně takové číslo z nějakého intervalu, pro které to bude trvat nejvíce kroků.
Tvar vstupu: První řádek vstupu bude obsahovat číslo K. Na každém z následujících K řádků bude jeden interval, který Kevina zajímá. Interval je zadaný jako dvojice čísel oddělených mezerou, přičemž krajní hodnoty do intervalu patří. Slibujeme, že spodní mez je vždy alespoň dva.
Tvar výstupu: Pro každý interval na vstupu vypište na samostatný řádek největší počet kroků a také první číslo z intervalu, pro něž se tohoto počtu kroků dosahuje.
2 10 20 23 44
20 18 111 27
28-Z2-3 Byli jsme tři (10 bodů)
Po obědě v bufetu leteckého muzea se Kevin, Sára a Petr posadili společně k jednomu stolu. Petr začal přemýšlet: „To je super, že se my tři tak dobře známe. Kolik si myslíte, že je ve škole ještě takových trojic?“
Sáře se najednou rozsvítily oči a vytáhla svůj sešit. Exponáty v muzeu ji tolik nezajímaly, tak si celý den zapisovala, kdo se s kým baví. Jejím tajným snem totiž bylo stát se špiónkou.
Trojice kamarádů se tedy podívala na to, co si Sára zapsala. Měla poznamenané všechny lidi ve škole, kteří se dobře znají, a my bychom chtěli spočítat počet trojic kamarádů, jako třeba Kevina, Sáru a Petra (zkrátka trojic, kde každý zná dobře každého).
Tvar vstupu: Na prvním řádku vstupu naleznete dvě čísla N a K oddělená mezerou – celkový počet žáků ve škole a počet dobrých přátelství, o kterých víme. Na dalších K řádcích je pak vždy dvojice čísel popisující, kdo s kým se přátelí (dvojice čísel oddělených mezerou, číslujeme od 0 do N-1).
Platí, že 1 < N,K ≤ 105.
Tvar výstupu: Do výstupního souboru vypište jediné číslo a to počet různých trojic kamarádů.
10 5 0 1 0 2 1 3 1 2 3 2
2
Poznámka: Existují právě dvě trojice, a to 012 a 123.
28-Z2-4 Rozsypaná turbína (12 bodů)
„Podíve…ach né!“ zakopl Kevin, když chtěl Sáře ukázat zajímavě vyskládané lopatky z turbíny proudového letadla. Lopatky se rozlétly do všech stran a zazvonily po podlaze haly. A kde se vzal, tu se vzal, stál nad Kevinem velký, zlý a tajemný hlídač.
Položil mu ruku na rameno se slovy: „Tak to si poskládáte, mladý muži. Doufám, že máte dostatek času.“
Každá lopatka z turbíny má na sobě dvě písmena (vrchní a spodní) a platí, že dvě lopatky mohou být za sebou jen tehdy, pokud vrchní písmeno na první je stejné jako spodní písmeno na druhé. Víme, že lopatky jdou určitě poskládat zpátky tak, aby na sebe všechny dokola navazovaly, pomozte je Kevinovi poskládat.
Tvar vstupu: Na prvním řádku dostanete počet lopatek. Na dalších řádcích je vždy dvojice písmen popisujících jednu lopatku (horní a dolní písmeno oddělené mezerou).
Tvar výstupu: Vypište lopatky v pořadí, v jakém se mají poskládat.
6 A A C B A C B A B D D B
C B B D D B B A A A A C
K této úloze jsme na Dnu otevřených dveří MFF UK ukázali drobnou nápovědu. Abychom byli spravedliví i k těm, kteří na DODu nebyli, můžete se podívat na záznam přednášky.
28-Z2-5 Příkop u Tří soutěsek (12 bodů)
Byl už večer, když konečně Kevina pustili z muzea. Zrovna pršelo. Jak tak čekal na zastávce autobusu, sledoval příkop vedle silnice postupně se plnící vodou.
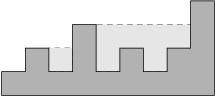
Příkop byl v různých částech různě hluboký a Kevina fascinovalo to, jak se voda různě přelévá a vytéká pryč. Když voda dotekla na nějaký okraj příkopu, zmizela v propustku pod silnicí, takže se držela jen v prohloubeninách.
Kevin se ještě chvíli díval a pak popadl tužku a papír s tím, že spočítá, kolik vody se může v příkopu zadržet. Předpokládejte, že máme podélný řez příkopem jako čtvercovou síť s přesností na decimetry (viz obrázek níže) a že příkop je široký také třeba decimetr. V takovém případě je objem vody v příkopu níže 7 litrů. Vymyslete algoritmus, který toto spočítá pro každý příkop.
28-Z2-6 Kalamita (14 bodů)
Jak nastoupil Kevin do autobusu, změnil se déšť ve sníh a během pár chvil celé město za okny autobusu pohltila sněhová vánice. Kevin se sice ještě dostal domů, ale dopravní podnik už začal plánovat, jaké zastávky bude muset přestat obsluhovat.
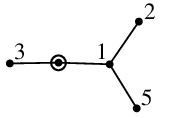
Dopravní podnik provozuje ve městě síť autobusů ve tvaru stromu (pokud neznáte stromy, podívejte se do základní kuchařky), které se všechny rozbíhají z centrálního přestupního stanoviště u vlakového nádraží. Pro každou zastávku zná dopravní podnik počet cestujících, kteří zde za den nastupují. Pokud zrušíme obsluhu nějaké zastávky, tak tím současně zrušíme i obsluhu všech zastávek za touto zastávkou (směrem dál od centrálního přestupu).
Dopravní podnik by potřeboval pořadí zastávek, v jakém je má postupně rušit, aby vždy odřízl od světa co nejméně cestujících.
Například pro síť na obrázku níže (čísla značí počet cestujících, kroužek centrální zastávku) se vyplatí postupně rušit zastávky se 2, 3, 5 a 1 cestujícím.
